Способ наименьших квадратов

В этом способе в качестве приближающей функции используется полином. Согласно этому способу за меру отклонения полинома

Q_m (x) = a ₀ + a ₁ x + … + a _m x ^m (10)

от данной функции f (x) на множестве точек x ₀, x ₁, …, x _n принимают величину

S _m = 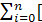Q_m(x_i) – f (x_i)]².

Очевидно, что S _m есть функция коэффициента а ₀, а ₁,…, а _m. Эти коэффициенты надо подобрать так, чтобы величина S _m была наименьшей. Для решения этой задачи найдём частные производные от величины

S _m = 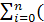a ₀ + a ₁x_i + a ₂x_i² + … + a _mx_i^m – y _i)².

Приравнивая эти частные производные к 0, получим для определения неизвестных a ₀, a ₁,…, a _m систему m +1 уравнений с m +1 неизвестными.

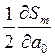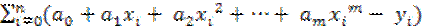= ·1 = 0,

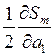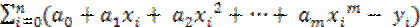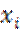= · = 0, (4.1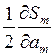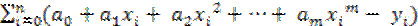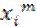0)

……………………………………………………………………………………………………………………………………….

= · = 0.

Здесь производная берётся от сложной функции, т.е.

S = [ a · γ + f ]²; S ’(a) = 2 [ a · γ + f ]· 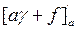= 2[ a · γ + f ] ·γ.

Введём обозначения

S _k = 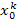+ + 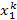… + 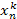(k = 0, 1, 2, …, 2 m),

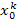
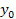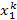
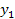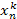
t _k = + + … + 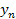(k = 0, 1, 2, …, 2 m), (4.11)

Учитывая эти обозначения, система (4.11) примет вид:

a ₀ S ₀ + a ₁ S ₁ + a ₂ S ₂ +…+ a _m S _m = t ₀,

a ₀ S ₁ + a ₁ S ₂ + a ₂ S ₃ +…+ a _m S _m+1 = t ₁, (4.12)

a ₀ S ₂ + a ₁ S ₃ + a ₂ S ₄ +…+ a _m S _m+2 = t ₂,

_{……………………………………………………….}

a ₀ S _m + a ₁ S _m+1 + a ₂ S _m+2 +…+ a _m S _2m = t _m,

где S ₀ = n +1.

Можно доказать, что если среди точек х ₀, х ₁,…, х _n нет совпадающих и m ≤ n, то определителем системы (4.12) ≠ 0 и следовательно эта система имеет единственное решение a ₀= 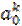, a ₁= 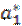, …, a_m= 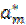. Полином (4.10) с такими коэффициентами будет обладать минимальным квадратным отклонением.

Для составления системы (4.12) рекомендуется схема решения по способу наименьших квадратов, приведённая в таблице 6, где принято m =2, n =4.

Таблица 6

x 0	x	x 2	x 3	x 4	y	xy	x 2 y
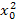
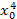
	x 0				y 0	x 0 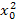y 0	y 0
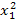
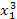
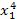
	x 1				y 1	x 1 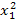y 1	y 1
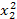
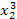
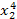
	x 2				y 2	x 2 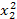y 2	y 2
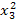
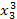
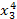
	x 3				y 3	x 3 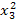y 3	y 3
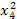
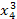
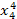
	x 4				y 4	x 4 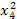y 4	y 4
S 0	S 1	S 2	S 3	S 4	t 0	t 1	t 2

Пример. Подобрать приближающий полином второй степени y=a₀ + a₁x + a₂x² для данных приведённых в таблице 7.

x	0,78	1,56	2,34	3,12	3,81
y	2,50	1,2	1,12	2,25	4,28

Таблица 7:

Решение. Составим числовую таблицу 8, для m =2, n =4, аналогичную таблице 6.

Таблица 8

x 0	x	x 2	x 3	x 4	y	xy	x 2 y
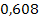
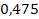
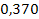
	0,78				2,50	1,950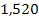
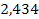
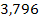
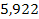
	1,56				1,20	1,872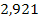
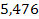
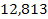
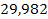
	2,34				1,12	2,621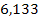
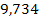
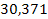
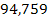
	3,12				2,25	7,020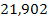
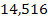
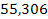
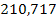
	3,81				4,28	16,307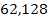
	11,61	32,768	102,761	341,750	11,35	29,770	94,604

Отсюда система (4.12) для определения коэффициентов a ₀, a ₁, a ₂ примет вид

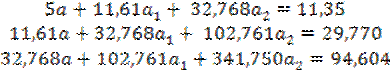
Решив эту систему, будем иметь a ₀=5,045, a ₂=1,009.

Следовательно, искомый полином будет иметь следующий вид

y = 5,045 – 4,043 х + 1,009 х ².