Если в пространстве заданы направляющий вектор прямой L
s = {l; m; n}и уравнение плоскости Ax + By + Сz + D = 0,
то угол между этой прямой и плоскостью можно найти используя формулу
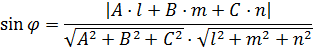
18. Уравнение прямой на плоскости с декартовой системой координат(виды уравнений прямой). Угловой коэффициент прямой. Расстояние от точки до прямой. Угол между прямыми. Уравнение высоты и медианы угла в треугольнике. Примеры.
 1)Уравнение прямой на плоскости с декартовой системой координат(виды уравнений прямой).
1)Уравнение прямой на плоскости с декартовой системой координат(виды уравнений прямой).
Вид уравнения прямой в прямоугольной системе координат Oxy на плоскости задает следующая теорема.
Теорема.
Всякое уравнение первой степени с двумя переменными x и y вида 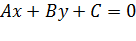 , где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и всякая прямая на плоскости задается уравнением вида
, где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и всякая прямая на плоскости задается уравнением вида 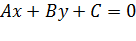 .
.
Уравнение 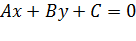 называется общим уравнением прямой на плоскости.
называется общим уравнением прямой на плоскости.
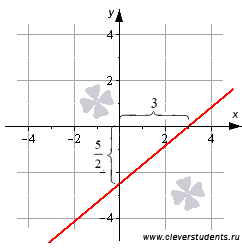
Уравнение прямой в отрезках.
Уравнение прямой вида 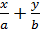 , где a и b – некоторые действительные числа отличные от нуля, называется уравнением прямой в отрезках.
, где a и b – некоторые действительные числа отличные от нуля, называется уравнением прямой в отрезках.
Для примера построим прямую линию, заданную уравнением в отрезках вида 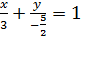 .Отмечаем точки
.Отмечаем точки 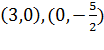 и соединяем их.
и соединяем их.
Уравнение прямой с угловым коэффициентом.
Уравнение прямой вида 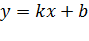 , где x и y - переменные, а k и b – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом (k – угловой коэффициент).
, где x и y - переменные, а k и b – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом (k – угловой коэффициент).
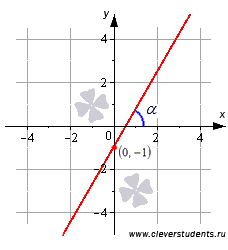 Угловой коэффициент прямой есть тангенс угла наклона этой прямой, то есть,
Угловой коэффициент прямой есть тангенс угла наклона этой прямой, то есть, 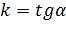 .
.
Если прямая параллельна оси ординат Oy, то угловой коэффициент обращается в бесконечность (угловой коэффициент не существует). Заметим, что прямая, определяемая уравнением 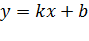 , проходит через точку
, проходит через точку 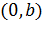 на оси ординат.
на оси ординат.
Таким образом, уравнение прямой с угловым коэффициентом 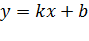 определяет на плоскости прямую, проходящую через точку
определяет на плоскости прямую, проходящую через точку 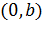 и образующую угол
и образующую угол 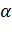 с положительным направлением оси абсцисс, причем
с положительным направлением оси абсцисс, причем 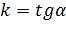 .
.
В качестве примера изобразим прямую, определяемую уравнением вида 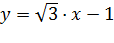 . Эта прямая проходит через точку
. Эта прямая проходит через точку 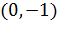 и имеет наклон
и имеет наклон 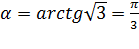 радиан (60 градусов) к положительному направлению оси Ox. Ее угловой коэффициент равен
радиан (60 градусов) к положительному направлению оси Ox. Ее угловой коэффициент равен 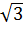 .
.
 Каноническое уравнение прямой на плоскости в прямоугольной декартовой системе координат Oxy имеет вид
Каноническое уравнение прямой на плоскости в прямоугольной декартовой системе координат Oxy имеет вид 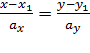 , где
, где 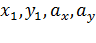 – некоторые действительные числа, причем
– некоторые действительные числа, причем 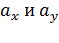 одновременно не равны нулю.
одновременно не равны нулю.
Пример.
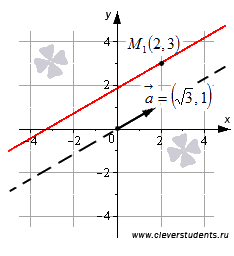
Изобразим на плоскости прямую линию, соответствующую каноническому уравнению прямой вида 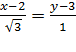 . Очевидно, что точка
. Очевидно, что точка 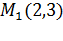 принадлежит прямой, а вектор
принадлежит прямой, а вектор 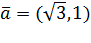 является направляющим вектором этой прямой.
является направляющим вектором этой прямой.
 Параметрические уравнения прямой на плоскости имеют вид
Параметрические уравнения прямой на плоскости имеют вид 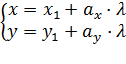 , где
, где 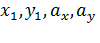 – некоторые действительные числа, причем
– некоторые действительные числа, причем 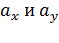 одновременно не равны нулю, а λ - параметр, принимающий любые действительные значения.
одновременно не равны нулю, а λ - параметр, принимающий любые действительные значения.
Пример.
Составьте параметрические уравнения прямой на плоскости в прямоугольной системе координат Oxy, если она проходит через точку 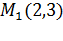 , а
, а 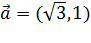 - ее направляющий вектор.
- ее направляющий вектор.
Решение.
Из условия имеем 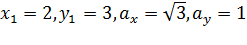 . Тогда параметрические уравнения прямой примут вид:
. Тогда параметрические уравнения прямой примут вид:
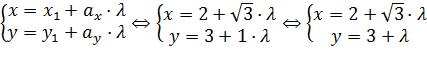 Для наглядности построим прямую на плоскости в прямоугольной системе координат Oxy, отвечающую найденным параметрическим уравнениям прямой:
Для наглядности построим прямую на плоскости в прямоугольной системе координат Oxy, отвечающую найденным параметрическим уравнениям прямой:
Нормальное уравнение прямой.
Если в общем уравнении прямой вида 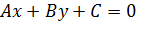 числа А, В и С таковы, что длина вектора
числа А, В и С таковы, что длина вектора 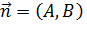 равна единице, а
равна единице, а 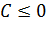 , то это общее уравнение прямой называется нормальным уравнением прямой.
, то это общее уравнение прямой называется нормальным уравнением прямой.
Часто можно видеть другую форму записи нормального уравнения прямой: 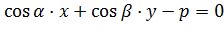 , где
, где 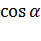 и
и 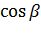 - действительные числа, представляющие собой направляющие косинусы нормального вектора прямой единичной длины (то есть,
- действительные числа, представляющие собой направляющие косинусы нормального вектора прямой единичной длины (то есть, 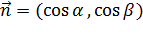 и справедливо равенство
и справедливо равенство 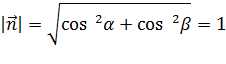 ), а величина p (
), а величина p (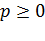 ) равна расстоянию от начала координат до прямой.
) равна расстоянию от начала координат до прямой.
Пример. Приведем общее уравнение прямой 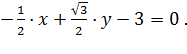 Это общее уравнение прямой является нормальным уравнением прямой, так как
Это общее уравнение прямой является нормальным уравнением прямой, так как 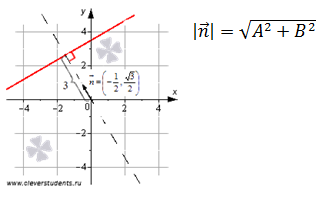 и
и 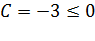 . Оно в прямоугольной системе координат Oxy на плоскости задает прямую линию, нормальный вектор которой имеет координаты
. Оно в прямоугольной системе координат Oxy на плоскости задает прямую линию, нормальный вектор которой имеет координаты 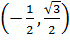 , и эта прямая удаленна от начала координат на 3 единицы в направлении нормального вектора
, и эта прямая удаленна от начала координат на 3 единицы в направлении нормального вектора 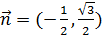 .
.
2)Расстояние от точки до прямой.
Расстояние d от точки Мо до прямой L равно модулю проекции вектора 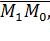 где
где 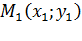 – произвольная точка прямой L, на направление нормального вектора
– произвольная точка прямой L, на направление нормального вектора 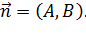
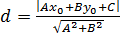
Пример.
Найти расстояние от точки Mo (2;-1) до прямой 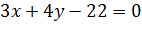 .
.
По формуле 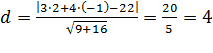
3)Угол между прямимы.
Определение. Если заданы две прямые 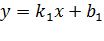 ,
, 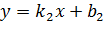 , то острый угол между этими прямыми будет определяться как
, то острый угол между этими прямыми будет определяться как 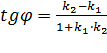 .
.
Две прямые параллельны, если k1 = k2. Две прямые перпендикулярны, если k1= -1/ k2.
4)Уравнение высоты и медианы угла в треугольнике.
Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. 
Из уравнения 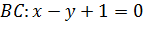 снимаем вектор нормали
снимаем вектор нормали 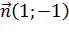 .
. 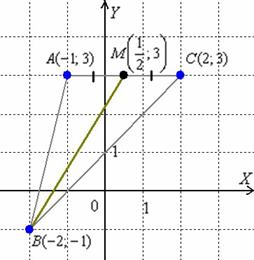 Уравнение высоты AH составим по точке
Уравнение высоты AH составим по точке 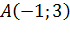 и направляющему вектору
и направляющему вектору 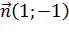 :
:
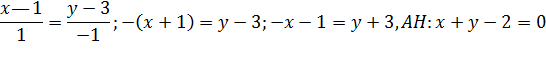 Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
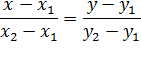 Найдём точку
Найдём точку 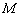 – середину стороны
– середину стороны 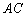 . Используем формулы координат середины отрезка. Известны координаты концов отрезка:
. Используем формулы координат середины отрезка. Известны координаты концов отрезка: 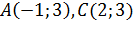 , тогда координаты середины:
, тогда координаты середины: 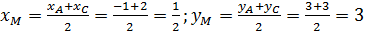 . Таким образом:
. Таким образом: 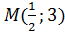 . Уравнение медианы BM составим по точкам
. Уравнение медианы BM составим по точкам 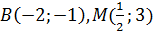 :
:
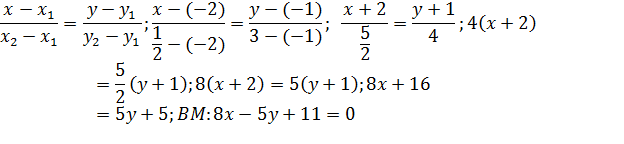
19. Эллипс на плоскости с декартовой системой координат (определение). Характеристики линии: полуоси, эксцентриситет. Каноническое уравнение эллипса с выводом. Качественное построение эллипса по каноническому уравнению. Примеры.
1)Эллипс на плоскости с декартовой системой координат(определение).
Эллипсом называется геометрическое место точек, для которых сумма расстояний от данных двух фиксированных точек плоскости есть величина постоянная. Причем необходимо, что бы эта постоянная была больше расстояний между фокусами
2)Характеристики линии.
Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
Отношение 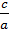 половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой
половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой 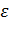 («эпсилон»):
(«эпсилон»): 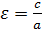
3)Каноническое уравнение эллипса с выводом.
Пусть F 1 и F 2 – фокусы, положим 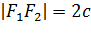 . Декартову систему координат зададим следующим образом: ось 0х направим по прямой F 1 F 2, а начало поместим в середину отрезка F 1 F 2. Тогда F 1(- с,0), F 2(с,0).
. Декартову систему координат зададим следующим образом: ось 0х направим по прямой F 1 F 2, а начало поместим в середину отрезка F 1 F 2. Тогда F 1(- с,0), F 2(с,0).
| M(x,y) |
| y |
| F1(-c,0) |
| O |
| F2(c,0) |
| x |
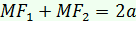 , где величина
, где величина 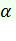 дана, причем
дана, причем 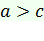 .
.Имеем:
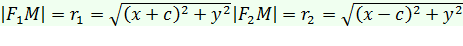
И, следовательно, уравнение эллипса примет вид 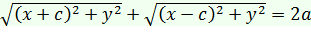
Перенесем один корень в правую часть равенства и возведем в квадрат:
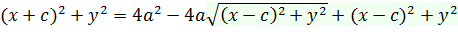 Сокращая, получаем:
Сокращая, получаем: 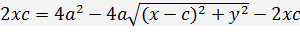
Приводим подобные, сокращаем на 4 и уединяем радикал: 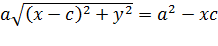
Возводим в квадрат: 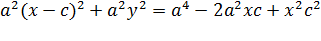
Раскрываем скобки и сокращаем на 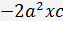 ;
; 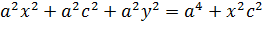
откуда получаем: 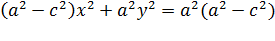
Используя равенство (2), получаем: 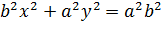 Разделив последнее равенство на
Разделив последнее равенство на 
получаем равенство 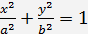
4)Качественное построение эллипса по каноническому уравнению.
Установим форму эллипса, пользуясь его каноническим уравнением.
1. Уравнение (11.7) содержит х и у 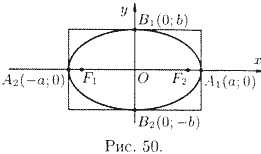 только в четных степенях, поэтому если точка (x,y) принадлежит эллипсу, то ему также принадлежат точки (x;-y),(-x;y),(-x;-y). Отсюда следует, что эллипс симметричен относительно осей Ox и Oy, а также относительно точки O(0;0), которую называют центром эллипса.
только в четных степенях, поэтому если точка (x,y) принадлежит эллипсу, то ему также принадлежат точки (x;-y),(-x;y),(-x;-y). Отсюда следует, что эллипс симметричен относительно осей Ox и Oy, а также относительно точки O(0;0), которую называют центром эллипса.
2. Найдем точки пересечения эллипса с осями координат. Положив y=0, находим две точки 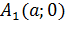 и
и 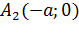 , в которых ось Ox пересекает эллипс (см. рис. 50). Положив в уравнении (11.7) x=0, находим точки пересечения эллипса с осью Oy:
, в которых ось Ox пересекает эллипс (см. рис. 50). Положив в уравнении (11.7) x=0, находим точки пересечения эллипса с осью Oy: 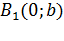 и
и 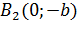 . Точки A 1, A2, B1, B2 называются вершинами эллипса. Отрезки A 1 A2 и B1B2, а также их длины 2 a и 2 b называются соответственно большой и малой осями эллипса. Числа a и b называются соответственно большой и малой полуосями эллипса.
. Точки A 1, A2, B1, B2 называются вершинами эллипса. Отрезки A 1 A2 и B1B2, а также их длины 2 a и 2 b называются соответственно большой и малой осями эллипса. Числа a и b называются соответственно большой и малой полуосями эллипса.
3. Из уравнения (11.7) следует, что каждое слагаемое в левой части не превосходит единицы,т.е. имеют место неравенства 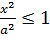 и
и 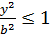 или
или 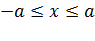 и
и 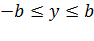 . Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми
. Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми 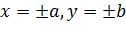 .
.
4. В уравнении (11.7) сумма неотрицательных слагаемых 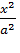 и
и 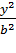 равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т. е. если
равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т. е. если 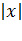 возрастает, то
возрастает, то 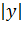 уменьшается и наоборот.Из сказанного следует, что эллипс имеет форму, изображенную на рис. 50 (овальная замкнутая кривая).
уменьшается и наоборот.Из сказанного следует, что эллипс имеет форму, изображенную на рис. 50 (овальная замкнутая кривая).
20. Гипербола на плоскости с декартовой системой координат (определение).Характеристики линии: полуоси, эксцентриситет. Канонические уравнения гипербол. Качественное построение гиперболы по каноническому уравнению. Примеры.
1)Гипербола на плоскости с декартовой системой координат (определение).
Гиперболой называется геометрическое место точек плоскости, разность расстояний от которых до двух заданных точек F 1, F 2 есть фиксированное число, взятое со знаком "+" или "–". Точки F 1, F 2 называются фокусами гиперболы.
Число a называется действительной полуосью гиперболы, а число b – ее мнимой полуосью .
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к величине действительной оси гиперболы, обозначается 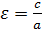 .
.
2)Канонические уравнения гипербол.
Обозначим фокусы через F1 и F2 расстояние 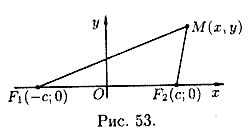 между ними через 2с, а модуль разности расстояний от каждой точки гиперболы до фокусов через 2a. По определению 2a < 2с, т. е. a < c.
между ними через 2с, а модуль разности расстояний от каждой точки гиперболы до фокусов через 2a. По определению 2a < 2с, т. е. a < c.
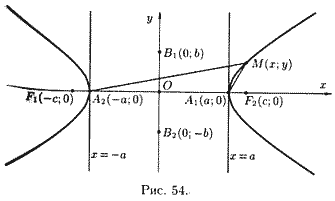
Для вывода уравнения гиперболы выберем систему координат Оху так, чтобы фокусы F1 и F2 лежали на оси Ох, а начало координат совпало с серединой отрезка F1F2 (см. рис. 53). Тогда фокусы будут иметь координаты F 1(- с,0), F 2(с,0). Пусть М(х,у) — произвольная точка гиперболы. Тогда согласно определению гиперболы 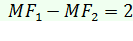 , т.е
, т.е 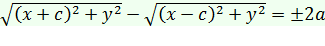 . После упрощений, как это было сделано при выводе уравнения эллипса, получим каноническое уравнение гиперболы
. После упрощений, как это было сделано при выводе уравнения эллипса, получим каноническое уравнение гиперболы 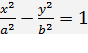 ,где
,где 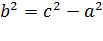 Гипербола есть линия второго порядка.
Гипербола есть линия второго порядка.
3)Качественное построение гиперболы по каноническому уравнению.
Установим форму гиперболы, пользуясь ее каноническим уравнением.
1. Уравнение (11.9) содержит x и у только в четных степенях. Следовательно, гипербола симметрична относительно осей Ox и Oy, а также относительно точки O(0;0), которую называют центром гиперболы.
2. Найдем точки пересечения гиперболы с осями координат. Положив y=0 в уравнении (11.9), находим две точки пересечения гиперболы с осью Ox: 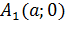 и
и 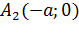 . Положив x=0 в (11.9), получаем
. Положив x=0 в (11.9), получаем 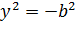 , чего быть не может. Следовательно, гипербола ось Оу не пересекает.
, чего быть не может. Следовательно, гипербола ось Оу не пересекает.
Точки 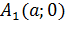 и
и 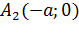 называются вершинами гиперболы, а отрезок
называются вершинами гиперболы, а отрезок 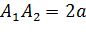 - действительной осью, отрезок
- действительной осью, отрезок 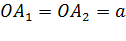 — действительной полуосью гиперболы.
— действительной полуосью гиперболы.
Отрезок 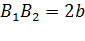 , соединяющий точки
, соединяющий точки 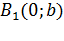 и
и 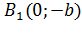 называется мнимой осью, число b - мнимой полуосью. Прямоугольник со сторонами 2a и 2b называется основным прямоугольником гиперболы.
называется мнимой осью, число b - мнимой полуосью. Прямоугольник со сторонами 2a и 2b называется основным прямоугольником гиперболы.
 3. Из уравнения (11.9) следует, что уменьшаемое
3. Из уравнения (11.9) следует, что уменьшаемое 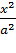 не меньше единицы т.е.что
не меньше единицы т.е.что 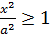 или
или 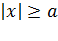 . Это означает, что точки гиперболы расположены справа от прямой x=a (правая ветвь гиперболы) и слева от прямой x=-a (левая ветвь гиперболы).
. Это означает, что точки гиперболы расположены справа от прямой x=a (правая ветвь гиперболы) и слева от прямой x=-a (левая ветвь гиперболы).
4. Из уравнения (11.9) гиперболы видно, что когда 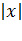 возрастает, то и
возрастает, то и 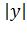 возрастает. Это следует из того, что разность
возрастает. Это следует из того, что разность 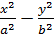 сохраняет постоянное значение, равное единице. Из сказанного следует, что гипербола имеет форму, изображенную на рисунке 54 (кривая, состоящая из двух неограниченных ветвей).
сохраняет постоянное значение, равное единице. Из сказанного следует, что гипербола имеет форму, изображенную на рисунке 54 (кривая, состоящая из двух неограниченных ветвей).
21. Парабола на плоскости с декартовой системой координат(определение). Уравнение параболы с выводом. Качественное построение гиперболы по уравнению. Примеры.
1)Каноническое уравнение параболы.
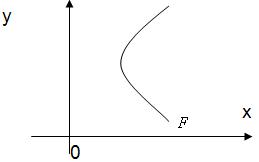
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p (p > 0).
Для вывода уравнения параболы выберем систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе в направлении от директрисы к F, а начало координат О расположим посередине между фокусом и директрисой (см. рис. 60). В выбранной системе фокус F имеет координаты 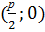 , а уравнение директрисы имеет вид
, а уравнение директрисы имеет вид 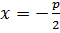 , или
, или 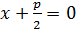 .
.
Пусть M(x,y) — произвольная точка параболы. Соединим точку Μ с F. 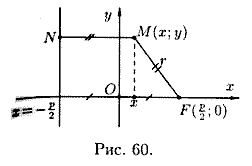 Проведем отрезок ΜΝ перпендикулярно директрисе. Согласно определению параболы MF = ΜΝ. По формуле расстояния между двумя точками находим:
Проведем отрезок ΜΝ перпендикулярно директрисе. Согласно определению параболы MF = ΜΝ. По формуле расстояния между двумя точками находим:
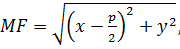 a
a 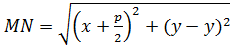 .Следовательно,
.Следовательно, 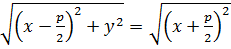 .Возведя обе части уравнения в квадрат, получим
.Возведя обе части уравнения в квадрат, получим 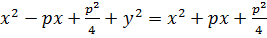 т. е.
т. е. 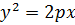 - каноническим уравнением параболы. Парабола есть линия второго порядка.
- каноническим уравнением параболы. Парабола есть линия второго порядка.
Исследование форм параболы по ее уравнению 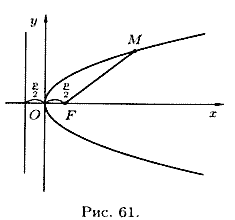
1. В уравнении (11.13) переменная y входит в четной степени, значит, парабола симметрична относительно оси Ox; ось Ox является осью симметрии параболы.
2. Так как ρ > 0, то из (11.13) следует, что  . Следовательно, парабола расположена справа от оси Оу.
. Следовательно, парабола расположена справа от оси Оу.
3. При x=0 имеем у = 0. Следовательно, парабола проходит через начало координат.
4. При неограниченном возрастании x модуль у также неограниченно возрастает. Парабола 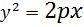 имеет вид (форму), изображенный на рисунке 61. Точка О(0; 0) называется вершиной параболы, отрезок FM = r называется фокальным радиусом точки М.
имеет вид (форму), изображенный на рисунке 61. Точка О(0; 0) называется вершиной параболы, отрезок FM = r называется фокальным радиусом точки М.
Пример. Составить уравнение геометрического места точек, равноотстоящего от оси Оу и точки 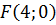
Решение: Возьмем на искомой линии произвольную точку 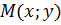 . Расстояние точки М от точки F определится по формуле расстояния между двумя точками:
. Расстояние точки М от точки F определится по формуле расстояния между двумя точками: 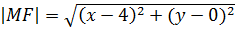
Расстояние точки М до оси Оу определится: 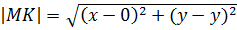
Так как по условию 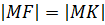 , то искомая кривая имеет уравнение:
, то искомая кривая имеет уравнение: 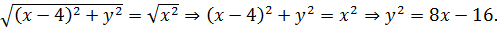
Линия, определяемая полученным уравнением 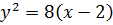 является параболой.
является параболой.
22. Полярная система координат и её связь с ДСК. Уравнение прямой и окружности, проходящей через полюс, в полярной системе координат(с выводом). Примеры.
 1)Полярная система координат на плоскости.
1)Полярная система координат на плоскости.
Возьмем на данной плоскости произвольную точку О и назовем её полюсом. Проведем на данной плоскости из точки О направленный луч, который назовем полярным лучом. Пусть М – произвольная точка данной плоскости. Соединим точку М с полюсом отрезком прямой и назовем этот отрезок ОМ и его длину 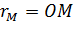 полярным радиусом точки М. Угол поворота
полярным радиусом точки М. Угол поворота 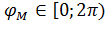 полярного луча вокруг полюса против часовой стрелки до совпадения с полярным радиусом точки М назовем полярным углом точки М.
полярного луча вокруг полюса против часовой стрелки до совпадения с полярным радиусом точки М назовем полярным углом точки М.
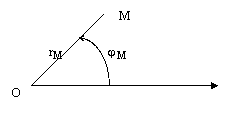 Упорядоченная пара действительных чисел
Упорядоченная пара действительных чисел 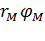 называется полярными координатами точки М. Полярной системой координат на плоскости называется полюс и полярный луч вместе с понятием полярных координат любой точки плоскости.
называется полярными координатами точки М. Полярной системой координат на плоскости называется полюс и полярный луч вместе с понятием полярных координат любой точки плоскости.
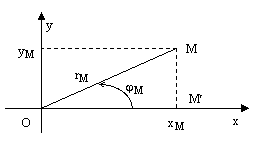
Связь полярной системы координат с ПДСК.
ПДСК на плоскости Оху стандартным образом совмещена с полярной системой координат этой же плоскости, если полюс полярной системы координат совпадает с началом координат ПДСК, а полярный луч совпадает с положительной полуосью оси абсцисс Ох.
 Положим для простоты обозначений:
Положим для простоты обозначений:
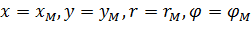 Тогда в этих обозначениях имеет место следующая теорема.
Тогда в этих обозначениях имеет место следующая теорема.
Теорема. Пусть ПДСК на плоскости Оху стандартным образом совмещена с полярной системой координат на этой же плоскости. Тогда декартовые координаты (х, у) любой точки плоскости связаны с её полярными координатами 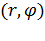 следующими соотношениями:
следующими соотношениями:
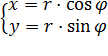 (1)
(1)
Доказательство. 1-й способ. Пусть точка М лежит в первой четверти. Тогда равенства (1) следуют из прямоугольного треугольника 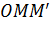 изображенного на рисунке.
изображенного на рисунке.
23. Уравнения кардиоиды, лемнискаты Бернулли, спирали Архимеда, логарифмической и гиперболической спиралей в полярной системе координат. Примеры.
Гиперболическая спираль —
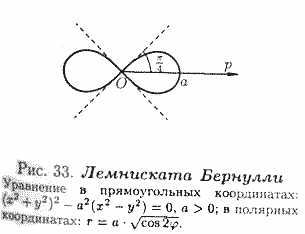
24. Кривые второго порядка на плоскости с полярной системой координат. Установление характеристик линий по уравнению в ПСК. Примеры.
1)Кривые второго порядка на плоскости.
Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат
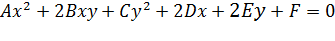 (11.1)
(11.1)
Коэффициенты уравнения — действительные числа, но по крайней мере одно из чисел А, В или С отлично от нуля. Такие линии называются линиями (кривыми) второго порядка. Ниже будет установлено, что уравнение (11.1) определяет на плоскости окружность, эллипс, гиперболу или параболу.
25. Функция и её график, основные свойства (область определения, множество значений, монотонность, ограниченность, четность/нечетность и периодичность функций) и способы задания. Примеры.
Понятие функции связано с установлением зависимости (связи) между элементами двух множеств.
Пусть даны два непустых множества X и Y. Соответствие ƒ, которое каждому элементу 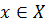 сопоставляет один и только один элемент у
сопоставляет один и только один элемент у 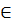 Y, называется функцией и записывается у=ƒ(х),
Y, называется функцией и записывается у=ƒ(х), 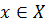 или ƒ: X→Y. Говорят еще, что функция ƒ отображает множество X на множество Y.
или ƒ: X→Y. Говорят еще, что функция ƒ отображает множество X на множество Y.
 Например, соответствия ƒ и g, изображенные на рисунке 98 а и б, являются функциями, а на рисунке 98 в и г — нет. В случае в — не каждому элементу
Например, соответствия ƒ и g, изображенные на рисунке 98 а и б, являются функциями, а на рисунке 98 в и г — нет. В случае в — не каждому элементу  соответствует элемент
соответствует элемент  . В случае г не соблюдается условие однозначности.
. В случае г не соблюдается условие однозначности.
Множество X называется областью определения функции ƒ и обозначается D(f). Множество всех 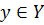 называется множеством значений функции ƒ и обозначается Е(ƒ).
называется множеством значений функции ƒ и обозначается Е(ƒ).
Числовые функции. График функции. Способы задания функций.
Пусть задана функция ƒ: X→Y.
Если элементами множеств X и Y являются действительные числа (т. е. 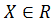 и
и 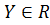 ), то функцию ƒ называют числовой функцией. В дальнейшем будем изучать (как правило) числовые функции, для краткости будем именовать их просто функциями и записывать у=ƒ(х).
), то функцию ƒ называют числовой функцией. В дальнейшем будем изучать (как правило) числовые функции, для краткости будем именовать их просто функциями и записывать у=ƒ(х).
Переменная х называется при этом аргументом или независимой переменной, а у — функцией или зависимой переменной (от х). Относительно самих величин х и у говорят, что они находятся в функциональной зависимости. Иногда функциональную зависимость у от х пишут в виде у=у(х), не вводя новой буквы (ƒ) для обозначения зависимости.
Частное значение функции ƒ(х) при х=a записывают так: ƒ(a). Например, если ƒ(х)=2х2-3, то ƒ(0)=-3, ƒ(2)=5.
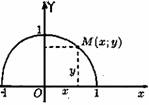
Графиком функции у=(х) называется множество всех точек плоскости Оху, для каждой на которых х является значением аргумента, а у — соответствующим значением функции.
Например, графиком функции у=√(1-х2) является верхняя полуокружность радиуса R=1 с центром в О(0;0) (см. рис. 99).
 Чтобы задать функцию у=ƒ(х), необходимо указать правило, позволяющее, зная х, находить соответствующее значение у. Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.
Чтобы задать функцию у=ƒ(х), необходимо указать правило, позволяющее, зная х, находить соответствующее значение у. Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.
Аналитический способ: функция задается в виде одной или нескольких формул или уравнений: 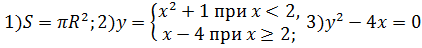
Если область определения функции у = ƒ(х) не указана, то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл. Так, областью определения функции у= √(1-х2) является отрезок [-1; 1].
Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию у=ƒ(х).
Графический способ: задается график функции.
Часто графики вычерчиваются автоматически самопишущими приборами или изображаются на экране дисплея. Значения функции у, соответствующие тем или иным значениям аргумента х, непосредственно находятся из этого графика.
Преимуществом графического задания является его наглядность, недостатком — его неточность.
Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений тригонометрических функций, логарифмические таблицы.
На практике часто приходится пользоваться таблицами значений функций, полученных опытным путем или в результате наблюдений.
Основные характеристики функции
1. Функция у=ƒ(х), определенная на множестве D, называется четной, если " xÎ D выполняются условия -хєD и ƒ(-х)=ƒ(х); нечетной, если " xєD выполняются условия -хєD и ƒ(-х)=-ƒ(х).
График четной функции симметричен относительно оси Оу, а нечетной — относительно начала координат.
Например, у=х2, у=√(1+х2), у=ln|х| — четные функции; а у=sinx, у=х3 — нечетные функции; у=х-1, у=√x — функции общего вида, т. е. не четные и не нечетные.
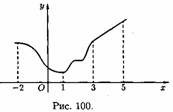
2. Пусть функция у=ƒ(х) определена на множестве D и пусть D 1єD. Если для любых значений х 1;x2єD1 аргументов из неравенства x1<x2 вытекает неравенство: ƒ(x 1)<ƒ(х2), то функция называется возрастающей на множестве D 1; f(x1) ≤ ƒ(х2), то функция называется неубывающей на множестве D1; f(x1)>ƒ(х2), то функция называется убывающей на множестве D1; ƒ(х1)≥ƒ(x2), то функция называется невозрастающей на множестве D1.
Например, функция, заданная графиком (см. рис. 100), убывает на интервале (-2; 1), не убывает на интервале (1; 5), возрастает на интервале (3; 5).
Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве D1 называются монотонными на этом множестве, а возрастающие и убывающие — строго монотонными. Интервалы, в которых функция монотонна, называются интервалами монотонности. На рисунке (выше) функция строго монотонна на (-2; 1) и (3; 5); монотонна на (1;3).
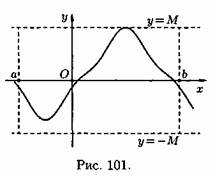
3. Функцию у=ƒ(х), определенную на множестве D, называют ограниченной на этом множестве, если существует такое число М>0, что для всех хєD выполняется неравенство |ƒ(х)|≤М (короткая запись: у=ƒ(х), хєD, называется ограниченной на D, если $М>0: """xєD ==>|ƒ(х)|≤М). Отсюда следует, что график ограниченной функции лежит между прямыми у=-М и у=М (см. рис. 101).
 4. Функция у=ƒ(х), определенная на множестве D, называется периодической на этом множестве, если существует такое число Т>0, что при каждом хєD значение (х+Т)єD и ƒ(х+Т)=ƒ(х). При этом число Т называется периодом функции. Если Т— период функции, то ее периодами будут также числа m•Т, где m=±1;±2,... Так, для у=sinx периодами будут числа ±2π;±4π; ±6π,... Основной период (наименьший положительный) — это период Т=2π. Вообще обычно за основной период берут наименьшее положительное число Т, удовлетворяющее равенству ƒ(х+Т)=ƒ(х).
4. Функция у=ƒ(х), определенная на множестве D, называется периодической на этом множестве, если существует такое число Т>0, что при каждом хєD значение (х+Т)єD и ƒ(х+Т)=ƒ(х). При этом число Т называется периодом функции. Если Т— период функции, то ее периодами будут также числа m•Т, где m=±1;±2,... Так, для у=sinx периодами будут числа ±2π;±4π; ±6π,... Основной период (наименьший положительный) — это период Т=2π. Вообще обычно за основной период берут наименьшее положительное число Т, удовлетворяющее равенству ƒ(х+Т)=ƒ(х).
26.  Графики основных элементарных функций. Примеры.
Графики основных элементарных функций. Примеры.
Основными элементарными функциями называют следующие функции.
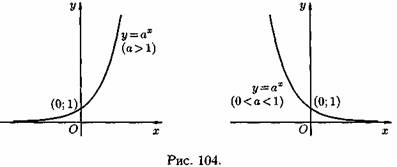
1) Показательная функция у=aх,a>0, а ≠ 1. На рис. 104 показаны графики показательных функций, соответствующие различным основаниям степени.
2) Степенная функция у=хα, αєR. Примеры графиков степенных функций, соответствующих различным показателям степени, предоставлены на рисунках
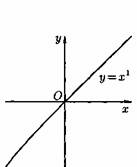
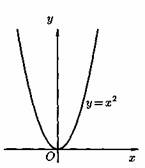
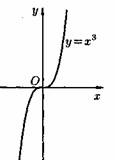
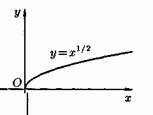
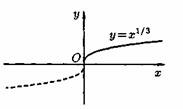
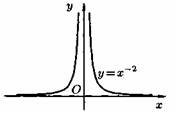
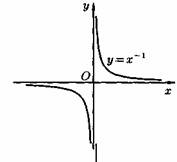
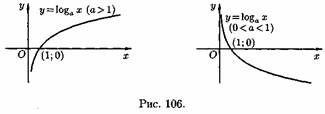 3)Логарифмическая функция y=logax, a>0,a≠1;Графики логарифмических функций, соответствующие различным основаниям, показаны на рис. 106.
3)Логарифмическая функция y=logax, a>0,a≠1;Графики логарифмических функций, соответствующие различным основаниям, показаны на рис. 106.
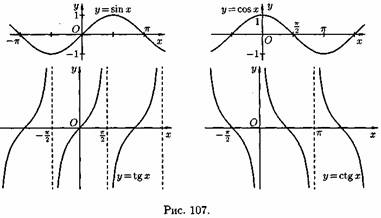
4) Тригонометрические функции у=sinx, у=cosx, у=tgх, у=ctgx; Графики тригонометрических функций имеют вид, показанный на рис. 107.
5) Обратные тригонометрические 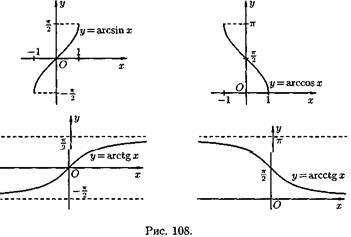 функции у=arcsinx, у=arccosх, у=arctgx, у=arcctgx. На рис. 108 показаны графики обратных тригонометрических функций.
функции у=arcsinx, у=arccosх, у=arctgx, у=arcctgx. На рис. 108 показаны графики обратных тригонометрических функций.
Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций взятия функции от функции, называется элементарной функцией.
Примерами элементарных функций могут служить функции 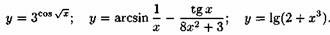
Примерами неэлементарных функций могут служить функции 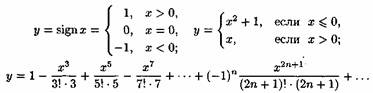
27. Числовая последовательность. Предел числовой последовательности (определение, сходящиеся и расходящиеся, ограниченные и неограниченные, монотонные последовательности). Примеры
Числовая последовательность
Под числовой последовательностью х1, х2, x3,..., хn... понимается функция
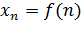 (15.1)
(15.1)
заданная на множестве N натуральных чисел. Кратко последовательность обозначается в виде {хn} или хn, nєN. Число x1 называется первым членом (элементом) последовательности, х2 — вторым,..., хn — общим или n-м членом последовательности.
Чаще всего последовательность задается формулой его общего члена. Формула (15.1) позволяет вычислить любой член последовательности по номеру, по ней можно сразу вычислить любой член последовательности. Так, равенства
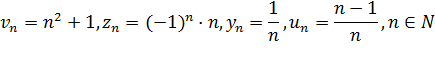 задают соответственно последовательности
задают соответственно последовательности
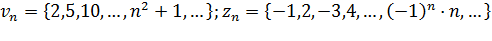
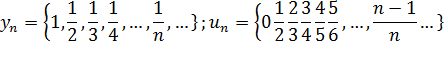
Последовательность {хn} называется ограниченной, если существует такое число М>0, что для любого nєN выполняется неравенство 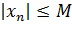
В противном случае последовательность называется неограниченной. Легко видеть, что последовательности уn и un ограничены, а νn и zn — неограничены.
Последовательность {хn} называется возрастающей (неубывающей), если для любого п выполняется неравенство an+1>an (an+1≥аn). Аналогично определяется убывающая (невозрастающая) последовательность.
Все эти последовательности называются монотонными последовательностями. Последовательности vn, yn, un монотонные, a zn — не монотонная.
Если все элементы последовательности {хn} равны одному и тому же числу с, то ее называют постоянной.
Другой способ задания числовых последовательностей — рекуррентный способ. В нем задается начальный элемент xi (первый член последовательности) и правило определения n-го элемента по (n-1)-му: xn=f(xn-1). Таким образом, x2=ƒ(xi), х3=ƒ(х2) и т. д. При таком способе задания последовательности для определения 100-го члена надо сначала посчитать все 99 предыдущих.
Предел числовой последовательности. Можно заметить, что члены последовательности un неограниченно приближаются к числу 1. В этом случае говорят, что последовательность un, nєN стремится к пределу 1.
Число α называется пределом последовательности (хn), если для любого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство
|хn-α|<ε (15.2)
В этом случае пишут 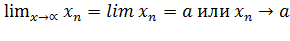 и говорят, что последовательность {хn} (или переменная хn, пробегающая последовательность x1, x2, х3,...) имеет предел, равный числу α (или хn стремится к α). Говорят также, что последовательность сходится к а.
и говорят, что последовательность {хn} (или переменная хn, пробегающая последовательность x1, x2, х3,...) имеет предел, равный числу α (или хn стремится к α). Говорят также, что последовательность сходится к а.
Коротко определение п редела можно записать так:
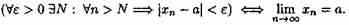
Пример (15.1):
xn=f(n) (15.1)
Заметим, что число N зависит от ε. Так, если ε =3/26, то
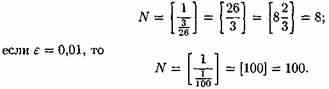
Поэтому иногда записывают N = N(ε).
Выясним геометрический смысл определения предела последовательности.
Неравенство (15.2) равносильно неравенствам —ε<хn-a<ε или a-ε<хn<a+ε,которые показывают, что элемент хn находится в ε-окрестности точки a.
Поэтому определение предела последовательности геометрически можно 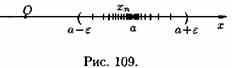 сформулировать так: число a называется пределом последовательности {xn}, если для любой ε-окресности точки a найдётся натуральное число N, что все значения хn, для которых n>N, попадут в ε-окрестность точки a (см. рис. 109).
сформулировать так: число a называется пределом последовательности {xn}, если для любой ε-окресности точки a найдётся натуральное число N, что все значения хn, для которых n>N, попадут в ε-окрестность точки a (см. рис. 109).
Ясно, что чем меньше ε, тем больше число N, но в любом случае внутри ε-окрестности точки a находится бесконечное число членов последовательности, а вне ее может быть лишь конечное их число.
Отсюда следует, что сходящаяся последовательность имеет только один предел. Последовательность, не имеющая предела, называется расходящейся. Таковой является, например, последовательность vn (см.5.1).
Постоянная последовательность хn=с, n є N имеет предел, равный числу с, т. е. lim с = с. Действительно, для "ε>0 при всех натуральных n выполняется неравенство (15.2). Имеем |xn-c|=|c-c|=0< ε.
28. Алгебраические свойства пределов последовательности. Теорема Вейерштрасса о пределе монотонной ограниченной последовательности. Примеры.
Свойства предела последовательности.
Определение 29. Последовательность называется финально постоянной, если 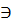 A
A 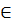 R и
R и 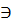 N, что для всех n>N xn = A.
N, что для всех n>N xn = A.
Теорема 7. (свойства предела последовательности)
1) Финально постоянная последовательность сходится.
2) Если последовательность сходится, то предел единственен.
3) Сходящаяся последовательность ограничена.
Доказательство.
1)Если xn = A при n>N, то для любой окрестности U(A) имеем xn 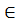 U(A) при n>N, то есть
U(A) при n>N, то есть 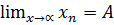 .
.
2)Пусть 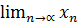 = A1 и
= A1 и 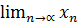 = A2, A1
= A2, A1 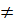 A2, тогда выберем
A2, тогда выберем 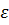 - окрестности точек A1, A2, так чтобы они не пересекались. В качестве
- окрестности точек A1, A2, так чтобы они не пересекались. В качестве 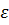 можно взять число
можно взять число 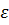 = 1/2|A1-A2|. По определению предела
= 1/2|A1-A2|. По определению предела 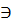 N1,N2, что при n>N1 xn
N1,N2, что при n>N1 xn 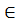 U(A1), а при n>N2 xn
U(A1), а при n>N2 xn 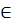 U(A2). Следовательно, при n> max{N1,N2} xn
U(A2). Следовательно, при n> max{N1,N2} xn 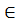 U(A1)
U(A1) 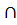 U(A2), что невозможно, так как U(A1)
U(A2), что невозможно, так как U(A1) 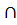 U(A2) =
U(A2) = 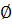 .
.
3)Пусть 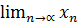 = A, положим в определении предела
= A, положим в определении предела 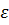 = 1, тогда
= 1, тогда 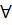 n>N |xn-A|< 1 значит |xn|<|A|+1. Выберем C>max{|x1|,...,|xN|,
n>N |xn-A|< 1 значит |xn|<|A|+1. Выберем C>max{|x1|,...,|xN|,
|A|+1}, тогда получим, что при 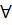 n
n 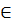 N |xn|< C.
N |xn|< C.
Предел монотонной ограниченной последовательности. Число е. Натуральные логарифмы
Теорема 15.3 (Вейерштрассa). Всякая монотонная ограниченная последовательность имеет предел.
В качестве примера на применение этого признака рассмотриv последовательность.
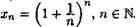
По формуле бинома Ньютона 
Из равенства (15.3) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число 1/n — убывает, поэтому величины (1-1/n), (1-1/n),... возрастают.
Поэтому последовательность {хn} = { (1+1/n)n }— возрастающая, при этом 
Покажем, что она ограничена. Заменим каждую скобку в правой части равенства (15.3) на единицу; правая часть увеличится, получим неравенство 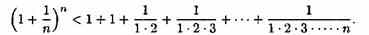
Усилим полученное неравенство, заменив числа 3, 4, 5,..., стоящие в знаменателях дробей, числом 2:
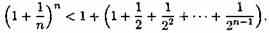
Сумму в скобке найдем по формуле суммы членов геометрической прогрессии:
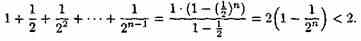
Поэтому
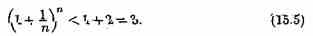
Итак, последовательность ограничена, при этом для n є N выполняются неравенства (15.4) и (15.5): 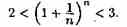
Следовательно, на основании теоремы Вейерштрасса последовательность имеет предел, обозначаемый обычно буквой е: 
Пример. Доказать, что последовательность 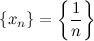 сходится.
сходится.
Доказательство. Рассматриваемая последовательность ограничена снизу, так как для любого натурального  :
: 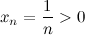
Исследуем заданную последовательность на монотонность:
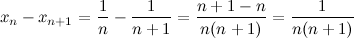
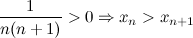 ,
,
а значит последовательность 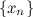 монотонно убывающая, а тогда, согласно теореме Вейерштрасса, последовательность сходится.
монотонно убывающая, а тогда, согласно теореме Вейерштрасса, последовательность сходится.
29. Предел функции в точке. Односторонние пределы (определение, геометрический смысл, связь односторонних пределов функции в точке с пределом функции в этой точке). Примеры.
Предел функции в точке
Пусть функция у=ƒ (х) определена в некоторой окрестности точки хо, кроме, быть может, самой точки хо.
Сформулируем два, эквивалентных между собой, определения предела функции в точке.
Определение 1 (на «языке последовательностей», или по Гейне).
Число А называется пределом функции у=ƒ(х) в топке x0 (или при х хо), если для любой последовательности допустимых значений аргумента xn, n є N (xnx0), сходящейся к хо последовательность соответствующих значений функции ƒ(хn), n є N, сходится к числу А
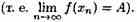
В этом случае пишут 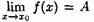
или ƒ(х)—>А при х→хо. Геометрический смысл предела функции: 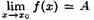 означает, что для всех точек х, достаточно близких к точке хо, соответствующие значения функции как угодно мало отличаются от числа А.
означает, что для всех точек х, достаточно близких к точке хо, соответствующие значения функции как угодно мало отличаются от числа А.
Определение 2 (на «языке ε», или по Коши).
Число А называется пределом функции в точке хо (или при х→хо), если для любого положительного ε найдется такое положительное число δ, что для все х 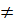 хо, удовлетворяющих неравенству|х-хо|<δ, выполняется неравенство |ƒ(х)А|<ε.
хо, удовлетворяющих неравенству|х-хо|<δ, выполняется неравенство |ƒ(х)А|<ε.
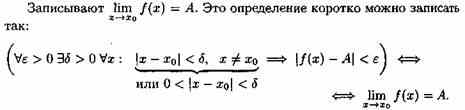
Геометрический смысл предела функции:
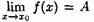
если для любой ε-окрестности точки А найдется такая δ-окрестность точки хо, что для всех х  хо из этой δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε, у=А-ε (см. рис. 110). Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).
хо из этой δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε, у=А-ε (см. рис. 110). Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).
Пример.
Доказать, что
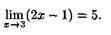
Решение: Возьмем произвольное ε>0, найдем δ=δ(ε)>0 такое, что для всех х, удовлетворяющих неравенству |х-3| < δ, выполняется неравенство |(2х-1)-5|<ε, т. е. |х-3|<ε.
Взяв δ=ε/2, видим, что для всех х, удовлетворяющих неравенству |х-3|< δ, выполняется неравенство |(2х-1)-5|<ε. Следовательно, lim(2x-1)=5 при х –>3. Пример.
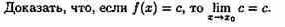
 Односторонние пределы
Односторонние пределы
В определении предела функции 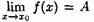 считается, что х стремится к x0 любым способом: оставаясь меньшим, чем x0(слева от х0), большим, чем хо (справа от хо), или колеблясь около точки x0.
считается, что х стремится к x0 любым способом: оставаясь меньшим, чем x0(слева от х0), большим, чем хо (справа от хо), или колеблясь около точки x0.
Бывают случаи, когда способ приближения аргумента х к хо существенно влияет на значение придела функции. Поэтому вводят понятия односторонних пределов.
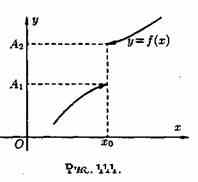
Число А1 называется пределом функции у=ƒ(х) слева в точке хо, если для любого число ε>0 существует число δ=δ(ε)> 0 такое, что при х є (х0-δ;xo), выполняется неравенство |ƒ(х)-А|<ε. Предел слева записывают так: limƒ(х)=А при х–>х0-0 или коротко: ƒ(хо-0)=А1 (обозначение Дирихле) (см. рис. 111).
Аналогично определяется предел функции справа, запишем его с помощью символов:
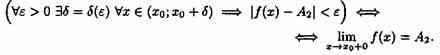
Коротко предел справа обозначают ƒ(хо+0)=А.
Пределы функции слева и справа называются односторонними пределами. Очевидно, если существует 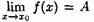 , то существуют и оба односторонних предела, причем А=А1=А2.
, то существуют и оба односторонних предела, причем А=А1=А2.
Справедливо и обратное утверждение: если существуют оба предела ƒ(х0-0) и ƒ(х0+0) и они равны, то существует предел 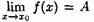 и А=ƒ(х0-0).
и А=ƒ(х0-0).
Если же А1 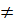 А2, то этот придел не существует.
А2, то этот придел не существует.
Пример. Найти односторонние пределы функции 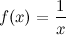 при
при 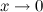
Решение. Правый предел: 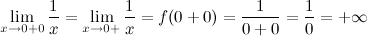 Левый предел:
Левый предел: 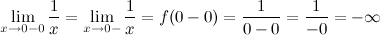
30. Предел функции «на бесконечности» (определения, геометрический смысл, алгебраические свойства пределов). Бесконечно большие и бесконечно малые (в точке и на бесконечности функции(определения). Примеры.
 Предел функции при х
Предел функции при х  ∞
∞
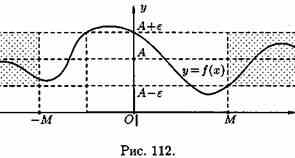
Пусть функция у=ƒ(х) определена в промежутке (-∞;∞). Число А называется пределом функции ƒ(х) при х→ ∞, если для любого положительного числа ε существует такое число М=М()>0, что при всех х, удовлетворяющих неравенству |х|>М выполняется неравенство |ƒ(х)-А|<ε. Коротко это определение можно записать так: 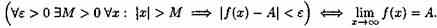
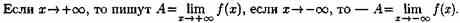
Геометрический смысл этого определения таков: для 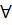 ε>0
ε>0 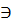 М>0, что при х є(-∞; -М) или х є(М; +∞) соответствующие значения функции ƒ(х) попадают в ε-окрестность точки А, т. е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у=А+ε и у=А-ε (см. рис. 112).
М>0, что при х є(-∞; -М) или х є(М; +∞) соответствующие значения функции ƒ(х) попадают в ε-окрестность точки А, т. е. точки графика лежат в полосе шириной 2ε, ограниченной прямыми у=А+ε и у=А-ε (см. рис. 112).
Бесконечно большая функция (б.б.ф.)
Функция у=ƒ(х) называется бесконечно большой при х→х0, если для любого числа М>0 существует число δ=δ(М)>0, что для всех х, удовлетворяющих неравенству 0<|х-хо|<δ, выполняется неравенство |ƒ(х)|>М. 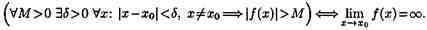
Например, функция у=1/(х-2) есть б.б.ф. при х—>2.
Если ƒ(х) стремится к бесконечности при х→хо и принимает лишь положительные значения, то пишут
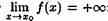
если лишь отрицательные значения, то
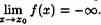
Функция у=ƒ(х), заданная на всей числовой прямой, называется бесконечно большой при х→∞, если для любого числа М>0 найдется такое число N=N(M)>0, что при всех х, удовлетворяющих неравенству |х|>N, выполняется неравенство |ƒ(х)|>М. Коротко: 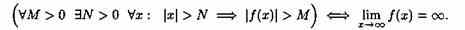
Например, у=2х есть б.б.ф. при х→∞.
Отметим, что если аргумент х, стремясь к бесконечности, принимает лишь натуральные значения, т. е. хєN, то соответствующая б.б.ф. становится бесконечно большой последовательностью. Например, последовательность vn=n2+1, n є N, является бесконечно большой последовательностью. Очевидно, всякая б.б.ф. в окрестности точки хо является неограниченной в этой окрестности. Обратное утверждение неверно: неограниченная функция может и не быть б.б.ф. (Например, у=хsinх.)
Однако, если limƒ(х)=А при х→x0, где А — конечное число, то функция ƒ(х) ограничена в окрестности точки хо.
Действительно, из определения предела функции следует, что при х→ х0 выполняется условие |ƒ(х)-А|<ε. Следовательно, А-ε<ƒ(х)<А+ε при х є (хо-ε; хо+ε), а это и означает, что функция ƒ (х) ограничена.
Бесконечно большой функцией в точке 0 является функция 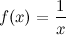
Функция
 2015-02-04
2015-02-04 3635
3635