Ан в секунду (рад/с)

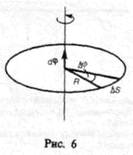
Линейная скорость точки (см. рис. 6)

Т. е.

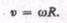
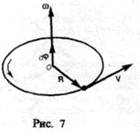
В векторном виде формулу для линейной скорости можно написать как векторное произведение: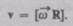

При этом модуль векторного произведения, по определению, равен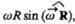

а направление совпадает с направлением поступательного движения правого винта при

его вращения от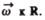

Если 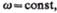то вращение равномерное и его можно характеризовать периодом

вращения Т — временем, за которое точка совершает один полный оборот, т. с. поворачивается на угол 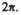Так как промежутку времени 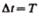соответствует

то 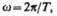откуда

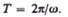
Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения:

откуда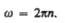

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

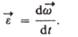
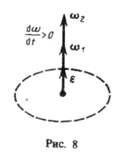
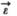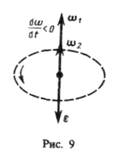
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор сонаправлен вектору 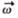(рис. 8), при замедлен­ном — противонаправлен ему (рис. 9).

Тангенциальная составляющая ускорения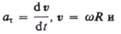

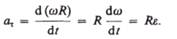
Нормальная составляющая ускорения

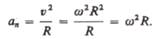
Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость 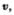тангенциальное ускорение 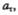нормальное ускорение 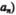и угловыми величинами (угол поворота 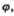угловая скорость 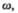угловое ускорение 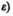выражается следующими формулами:

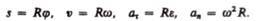
В случае равнопеременного движения точки по окружности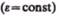

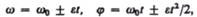
где 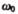— начальная угловая скорость.