2015-02-04
788
Дальнейшее повышение порядка точности формул, подобных квадратурным формулам центральных прямоугольников, трапеций, парабол, можно получить, применяя на отрезках разбиения интерполяцию функции f(x) многочленами более высокой степени (ниже мы использовали линейные функции, то есть многочлены степени 1, и квадратные трёхчлены — многочлены степени 2).
Например, если использовать кубическое интерполирование, то есть приближать функцию f(x) многочленами степени 3, то получится формула, называемая кквадратурной формулой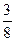 
(три восьмых):
, 
, 
,
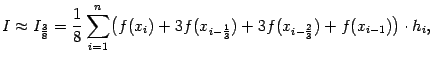
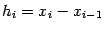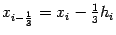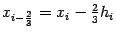то есть точк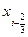и 
и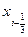 
делят отрезок разбиения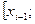 
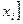на три равных части. Число 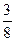в названии формулы связано с тем, что если положить hi= 
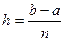, постоянным и ввести обозначение 
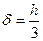, то формула получает вид
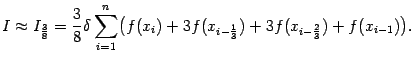
Если же использовать для интерполяции многочлены шестой степени Pi(x) и заменять интеграл от f(x) на каждом из отрезков 
на интеграл от Pi(x), то получится квадратурная формула, называемая формулой Уэддля:
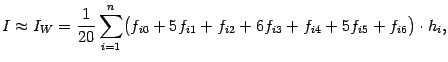
где hi=xi-xi-1 и fij=f(xi-1+j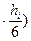 
Таким образом, при применении формулы Уэддля на каждом очередном отрезке нужно вычислить 6 новых значений функции 
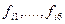, а значение 
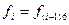вычислять заново не нужно, оно было уже вычислено на предыдущем шаге.
|
|
|
Для ошибки формулы Уэддля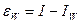 
с постоянным шагом hi= 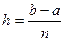, имеется такая оценка:
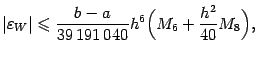
где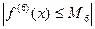 
и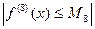 
при всех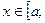 
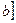. При этом предполагается, что восьмая производная f(8)(x) непрерывна на отрезке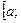 
.
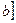Таким образом, формула Уэддля является квадраткрной формулой шестого порядка точности. На практике формулы более высокого порядка точности, чем формула Уэддля, не используются. Формула " 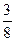" используется редко. Если не устраивает формула Симпсона, то сразу переходят к формуле Уэддля.
