Квадратурная формула Симпсона (формула парабол)

При выводе двух предыдущих квадратурных формул мы приближали график подынтегральной функции f(x)на каждом из отрезков разбиения 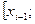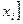прямой линией: либо касательной в формуле центральных прямоугольников, либо хордой в формуле трапеций. Очередным по сложности шагом является выбор приближения графика функции f(x)в виде параболы — графика некоторого квадратного трёхчлена Pi(x). Его вид, конечно, будет зависеть от отрезка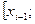 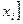, на котором мы выбираем приближение.

Выберем, например, такой квадратный трёхчлен Pi(x), чтобы его значения в точках 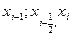и совпадали со значениями функции f(x)в этих же точках:

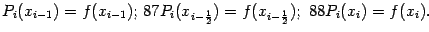(3)

Напомним, что через 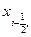мы обозначали середину отрезка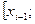 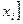, то есть 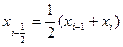Функцию можно записать в виде

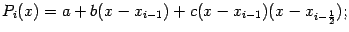
действительно, раскрыв скобки, получим некоторый квадратный трёхчлен. Подберём числа a,b,c так, чтобы выполнялись равенства (3).

Положим hi=xi-xi-1, тогда 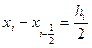и 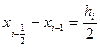. Подставим x=xi-1 в выражение для Pi(x) и получим:

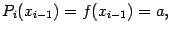
то есть

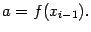
Подстановка 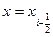даёт

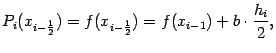
откуда

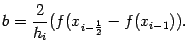
Наконец, подставим x=xi и получим

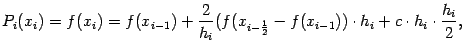
откуда

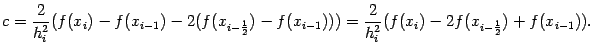
Вычислим теперь интеграл от интерполяционной функции Pi(x), для чего сделаем в нём заменуt=x-xi-1:

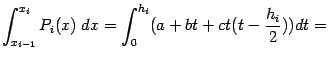
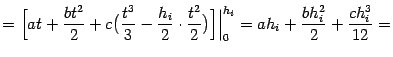
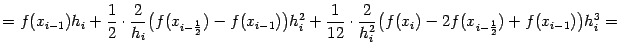
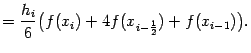
Осталось просуммировать эти величины по всем отрезкам разбиения. При этом получаем квадратурную формулу, которая называется формулой Симпсона, илиформулой парабол:

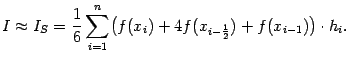
Нетрудно видеть, что это в точности та же "комбинированная" квадратурная формула (5.2), которую мы получили выше из формул центральных прямоугольников и трапеций.

Замечание При вычислении очередного слагаемого

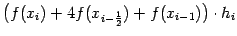
требуется вычислить только два (а не три) новых значения функции f(x), а именно, значения f(x_i) и f(x 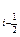). Значение f(x 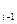) использовалось на предыдущем шаге и было тогда уже вычислено.

Если при применении формулы Симпсона взять все отрезки разбиения одинаковой длины h_i= 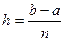, то формула Симпсона получает вид

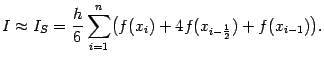(4)

Раскрыв скобки и объединив одинаковые слагаемые, можно легко привести эту формулу к виду

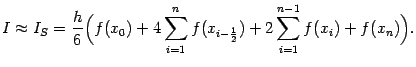
Действительно, слагаемые с целыми номерами (кроме f(x₀)=f(a) и f(x_n)=f(b)) входят по одному разу в каждое их двух соседних слагаемых в сумме (4), так что для них получается сумма с коэффициентом 2.

Оценка ошибки формулы Симпсона, то есть величины 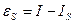, такова. Предположим, что функция f(x) имеет на отрезке 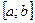непрерывную четвёртую производную f⁽⁴⁾(x), причём

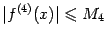
при всех 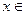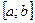. Тогда при выборе постоянного шага h_i= 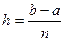, имеет место неравенство

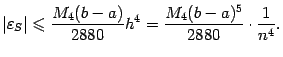
Таким образом, формула Симпсона — это квадратурная формула четвёртого порядка точности. Это означает, что при уменьшении шага 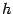вдвое ошибка 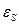уменьшится примерно в 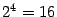раз, а при уменьшении шага в 10 раз ошибка уменьшится примерно в 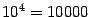раз.