Статически неопределимые системы при растяжении и сжатии и их расчет

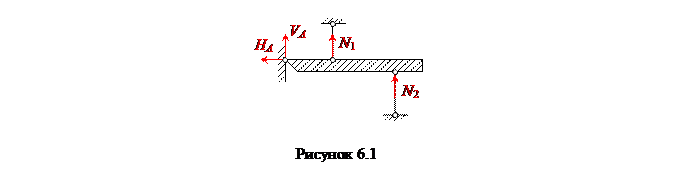
Система, изображенная на рисунке 6.1, считается статически неопределимой, так как можно составить для этой системы только три уравнения статики, а неизвестных реакций связи четыре.

Статически неопределимой системой называется система, в которой число неизвестных усилий (например, реакций связи) превышает число уравнений статики.

Степень статически неопределимой системы представляет собой разность между числом неизвестных усилий и числом уравнений статики.

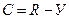(6.1)*

Для случая, приведенного на рисунке 6.1,

С = 4 – 3 = 1.

В статически неопределимой системе существуют так называемые «лишние» связи, устранение которых не нарушает геометрической неизменяемости всей системы, то есть не превращает систему в механизм.

Степень статически неопределимой системы характеризует число «лишних» связей системы, и тем самым обуславливает количество дополнительных уравнений, необходимых для раскрытия статической неопределимости системы.

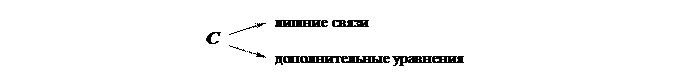
Статически неопределимые системы являются более прочными, жесткими и устойчивыми, однако обладают рядом особенностей, которые принято представлять в виде трех основных свойств статически неопределимых систем.

СВОЙСТВА СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ:

– свойство жесткости – усилия в элементах статически неопределимых систем распределяются пропорционально их жесткости независимо от абсолютных размеров этих элементов;

– свойство о монтажных напряжениях – при неточном изготовлении или сборке элементов статически неопределимых систем в них возникают дополнительные напряжения, называемые монтажными напряжениями;

– свойство о температурных напряжениях – при изменении температуры окружающей среды в элементах статически неопределимых систем возникают температурные напряжения.

где a – коэффициент линейного температурного расширения [град^–1].

Для решения статически неопределимых систем или раскрытия их статической неопределимости в курсе сопротивления материалов используется метод сил. Рассмотрим его применение на примере следующей жесткой балки, имеющей крепление в виде двух стержней (рисунок 6.2). Определим усилия, возникающие в этих стержнях.

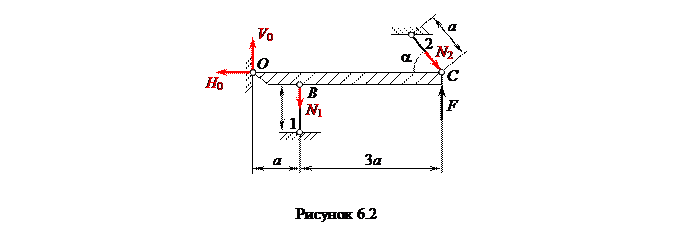
Дано: [s] = 160 МПа;

F = 800 кН;

А ₁: А ₂ = 2: 1;

a = 60°.

Найти: А ₁ и А ₂ – площади сечения стержней 1 и 2.

Решение

Решение статически неопределимых систем выполняется в четыре этапа путем рассмотрения четырех сторон задачи.

I сторона задачи – статическая.

Определяется степень статической неопределимости системы и составляется достаточное и необходимое количество уравнений статики.

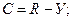
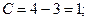
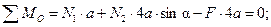
– уравнение равновесия

(6.3)

II сторона задачи – геометрическая (рисунок 6.3).

Исходная схема статически неопределимой системы изображается в условно деформированном состоянии согласно известного принципа возможных малых перемещений.

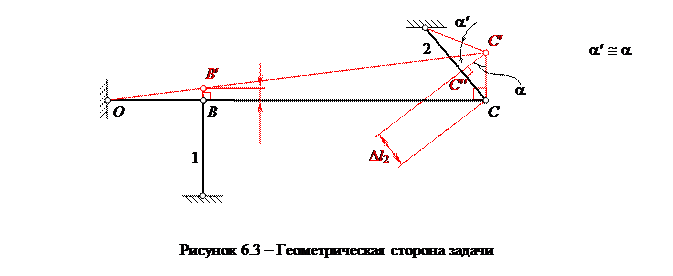
Из геометрического рисунка находится зависимость между деформациями элементов статически неопределимой системы. Полученное уравнение называется уравнением совместимости деформаций.

D ОВВ ¢ 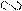DО СС ¢;

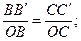
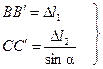
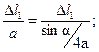
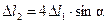(6.4)

III сторона задачи – физическая.

Чтобы связать уравнения (6.3) и (6.4) необходимо вспомнить некую физическую зависимость. Деформации элементов статически неопределимой системы представляются через усилия в них с использованием закона Гука в следующем виде:

IV сторона задачи – синтез.

Синтез означает сбор чего-то общего из отдельных частей.

Решаются совместно уравнения (6.3), (6.4) и (6.5). В итоге определяются искомые усилия в элементах статически неопределимой системы.

Подставляем(6.5) в (6.4), получим:

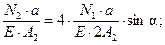
Подставляем (6.6) в (6.3), получим:

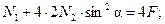
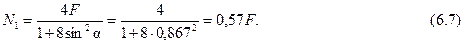
Подставляем (6.7) в (6.6), получим:

Производим подбор сечений стержней по принципу допускаемых напряжений, для этого устанавливаем более нагруженный стержень.

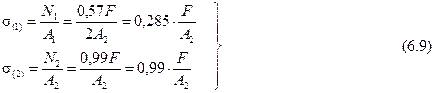
Выполняем проектировочный расчет по второму стержню.

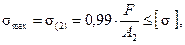
откуда

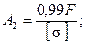
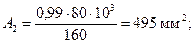
тогда

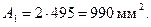
Выполняем подбор сечений стержней по принципу разрушающих нагрузок, для этого запишем уравнение равновесия (6.3) в виде уравнения появления текучести в элементах статически неопределимых систем.

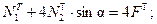
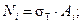
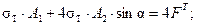
Разделим обе части уравнения на n – коэффициент запаса прочности.

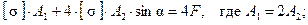
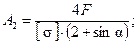
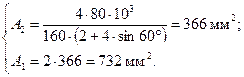
Имеем:

при расчете по принципу разрушающих нагрузок: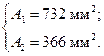

при расчете по принципу допускаемых напряжений: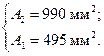

Таким образом, сравнивая два принципа расчета, видим, что расчет по принципу допускаемых нагрузок является более надежным, а расчет по принципу разрушающих нагрузок – более экономичным. В итоге, принимаем площади сечения стержней по первому (второму) принципу расчета для обеспечения большей надежности (экономичности), то есть

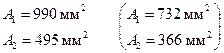
При этом, расхождение в расчетах составляет

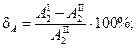
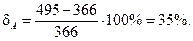
То есть конструкция при А ₁ = 990 мм², А ₂ = 495 мм² (А ₁ = 732 мм², А ₂ = 366 мм²) является на 35% надежнее (экономичнее).