2015-02-14
616
Как уже отмечалось, для построения окончательных эпюр внутренних сил в раме от воздействия заданной симметричной нагрузки, необходимо предварительно вычислить элементы матрицы податливости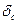 
, а для построения линий влияния - элементы обеих матриц 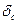и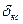 
. Целесообразно сделать проверку этих вычислений и получить обратные матрицы 
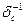и 
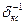,которые будут использованы в дальнейшем при решении систем канонических уравнений (1.3), (1.5) и (1.6) соответственно.
Вычисления осуществим по формуле Максвелла-Мора с использованием соответствующих правил (трапеций, Симпсона, Верещагина). Вначале вычислим перемещения от воздействия симметричных неизвестных равных единице. Все перемещения найдем, увеличенными на величину приведенной жесткости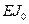 
.
= 
;
= 
;
= 
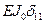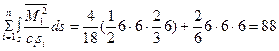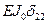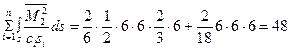Рис. 3
Тогда матрица dс приобретает следующий вид:
dс =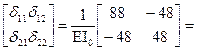 
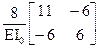(1.7)
Аналогично вычислим перемещения от воздействия кососимметричных единичных неизвестных:
;
.
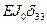
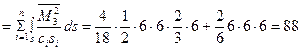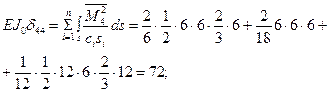
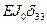
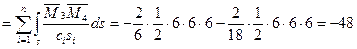Тогда матрица
dкс =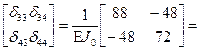 
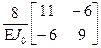(1,8)
С целью проверки коэффициентов канонических уравнений вычислим групповые перемещения d å,С и d å,КС, равные сумме всех перемещений соответственно от единичных симметричных и единичных кососимметричных неизвестных:
; 
,
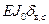
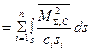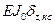
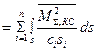где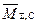 
, 
- суммарные единичные эпюры моментов (рис.3,д,е).
Сопрягая Эпюру 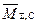саму с собой, получим
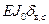
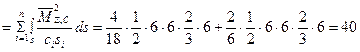
Сумма всех коэффициентов при симметричных неизвестных канонических уравнений (1.3, 1.5)
= 
;
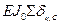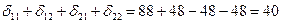(проверка выполняется)
Аналогично сопрягая эпюру саму с собой, получим
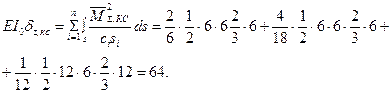
Сумма всех коэффициентов при кососимметричных неизвестных канонических уравнений (1.4, 1.6)
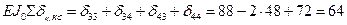
(проверка выполняется)
Получим обратные матрицы d с-1 и d кс–1, используя следующий алгоритм
.
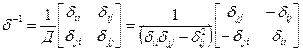Тогда
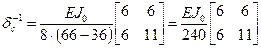; (1.9)
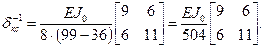(1.10)
