Вопросы и упражнения. 1. В чем заключается основная задача ньютоновской механики; динамики

1. В чем заключается основная задача ньютоновской механики; динамики?

2. Как в динамике определяются сила F и масса m? Каковы характерные свойства этих физических величин? В каких единицах они измеряются?

3. Как строятся системы единиц в механике? Какова роль формул размерностей?

4. Что называется импульсом р материальной точки?

5. Сформулируйте законы Ньютона. Какие утверждения содержат эти законы? Какова их взаимосвязь? Дайте определение понятий "инерция" и "инертность".

6. Какие системы отсчета называются инерциальными и неинерциальными? С какой степенью точности является инерциальной система отсчета: а) связанная с Солнцем и звездами (гелиоцентрическая); б) жестко связанная с Землей (лабораторная)?

7. Получите из общей формулировки второго закона Ньютона 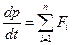основное уравнение динамики материальной точки .

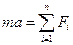8. Спроектировав уравнение динамики на оси х, у и z декартовой системы координат, получите три эквивалентных ему дифференциальных уравнения.

9. Каково содержание закона независимости действия сил? Сформулируйте принцип суперпозиции сил. Объясните задачу о лебеде, раке и щуке.

10. Введите понятие импульса силы. Объясните, почему пуля, вылетев из ружья, пробивает отверстие в стекле, не разбивая его, а надавливанием стержня на стекло этого сделать нельзя.

11. Назовите четыре типа фундаментальных взаимодействий. Какие силы рассматриваются в рамках ньютоновской механики?

12. Каковы границы применимости законов ньютоновской механики?

ЗАДАЧИ

2.1. Тело массой m = 0,5 кг движется прямолинейно, причем зависимость координаты х тела от времени описывается уравнением х = At² - Bt³, где А = 5 м/с², В = 1 м/с³. Найти силу, действующую на тело в конце первой секунды движения.

2.2. Под действием постоянной силы F = 10 Н тело движется прямолинейно так, что зависимость координаты х от времени описывается уравнением х = At². Найти массу тела, если постоянная А = 1 м/с².

2.3. Тело массой m = 0,5 кг движется так, что зависимость координаты х тела от времени описывается уравнением х = A sin ωt, где А = 5 см, ω = πc^-1.Найти силу, действующую на тело в момент t = 1/6 с.

2.4. Под действием одинаковых и постоянных сил два тела движутся прямолинейно так, что зависимости их координат от времени описываются уравнениями: х1 = At², х2 = ЗAt². Найти отношение масс этих тел.

2.5. Скорость частицы массой т, движущейся в плоскости ху, изменяется по закону v = Ati + Bt²j, где А и В — постоянные. Найти модуль результирующей силы, действующей на частицу, в зависимости от времени.

2.6. Материальная точка массой m = 20 г движется без трения прямолинейно под действием силы, изменяющейся со временем по закону F = At, где А – постоянный вектор, модуль которого А = 0,03 Н/с. В момент t = 0 координата тела х0 = 0, скорость v0 = 5 м/с. Записать зависимость координаты х движущейся точки от времени и найти путь, пройденный ею за первые 4 с.

2.7. В момент t = 0 частица массой т = 0,2 кг находилась в точке, координаты которой x0 = y0 = 0, и имела скорость v0 = Bi, где В = 2 м/с. В этот момент на нее начала действовать сила F = Аj, где А = 3 Н. Найти координаты х и у частицы в момент t = 3 с.

2.8. Частица массой т двигалась в плоскости ху со скоростью v = Аi + Вj, где А и В - постоянные. В момент t = 0 на частицу начала действовать сила F = Ctj. Найти: а) зависимость вектора скорости частицы от времени после начала действия силы; б) зависимость от времени угла, который составляет вектор скорости с осью х.

2.9. На покоившуюся частицу массой т в момент t = 0 начала действовать сила, изменяющаяся со временем по закону F = At (τ - t), где А – постоянный вектор, τ – время, в течение которого действует данная сила. Найти импульс частицы после окончания действия силы и путь, пройденный частицей за время действия силы.

2.10. Частица массой т в момент t = 0 начинает двигаться под действием силы F = F0 cos ωt, где F0 ω – постоянные. Найти: а) промежуток времени, в течение которого частица будет двигаться до первой остановки; б) максимальную скорость этого движения.

2.11. Масса автомобиля т = 10³ кг. Во время движения на него действует сила трения, равная 0,1 его силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, в случаях: а) равномерного движения; б) движения с ускорением а = 2,4 м/с².

2.12. На гладкой горизонтальной поверхности лежит 6 однородных кубиков одинаковой массы. На первый кубик в направлении, указанном на рис. 2.1 стрелкой, действует постоянная сила F. Найти модули результирующей силы f, действующей на каждый кубик, и силы f5,4, с которой четвертый кубик действует на пятый.

2.13. Тело массой т = 2,4 кг находится на пружинных весах, установленных в лифте. Лифт движется вверх с ускорением а = 4,9 м/с², направленным: а) вверх; б) вниз. Что покажут весы в обоих случаях?

2.14. Груз массой т = 2,1 кг, подвешенный к динамометру, один раз поднимают вверх, другой – опускают вниз с одним и тем же по модулю ускорением а = 3,2 м/с². Найти разность между показаниями динамометра в первом и во втором случаях.

2.15. Воздушный шар массой т = 1,6·10³ кг начал опускаться с постоянным ускорением. Если сбросить балласт массой Δm = 520 кг, то шар получит такое же ускорение, но направленное вверх. Найти: а) модуль подъемной силы, считая ее постоянной; б) модуль ускорения шара.

2.16. В вагоне, движущемся горизонтально и прямолинейно с ускорением а = 2 м/с², висит на шнуре груз массой т = 0,2 кг. Найти силу натяжения шнура и угол отклонения шнура от вертикали.

2.17. 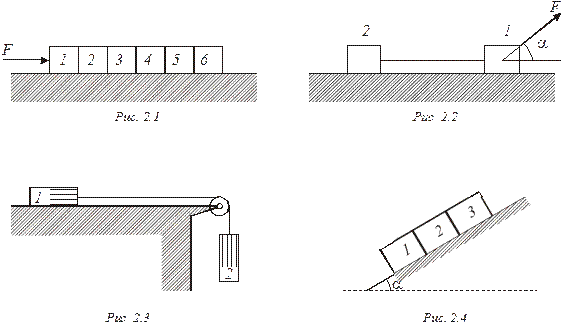Два тела массами m1 и m2, связанные между собой нитью, движутся по горизонтальной плоскости под действием силы F, которая приложена к первому телу (рис. 2.2) и все время составляет угол α с поверхностью. Коэффициент трения между телами и поверхностью одинаков и равен μ. Найти ускорение движения тел и силу натяжения нити между ними. Массой нити и растяжением пренебречь.

2.18. Грузы 1 и 2 скреплены невесомой нерастяжимой нитью, переброшенной через невесомый блок (рис. 2.3). Коэффициент трения между грузом 1 и горизонтальной поверхностью равен μ. Найти отношение масс т1/т2 грузов, если движение грузов: а) равномерное; б) с ускорением a.

2.19. В установке, представленной на рис. 2.3, грузы 1 и 2 массами т1 и т2, скрепленные невесомой и нерастяжимой нитью, движутся с постоянной скоростью. Найти ускорение, которое получат грузы, если на груз 2 положить перегрузок массой Δm. Коэффициент трения между грузом 1 и горизонтальной поверхностью остается одним и тем же. С какой силой перегрузок давит на груз 2? Массой блока и трением в блоке пренебречь.

2.20. Два груза соединены нерастяжимой однородной нитью длиной l так, как показано на рис. 2.3. Массы грузов т2 = т, m1 = (2/3)m, нити тн = (1/3) т. При какой длине вертикального отрезка нити силы, действующие на грузы со стороны нити, окажутся равными? Чему равны эти силы? Каково ускорение системы в этом случае? Массой блока и трением в блоке пренебречь.

2.21. 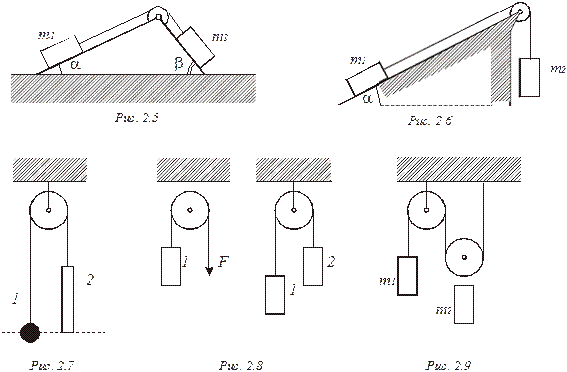На гладкую наклонную поверхность, составляющую угол α с горизонтом, поместили три соприкасающихся кубика, массы которых одинаковы (рис. 2.4). Найти: а) результирующую силу f, действующую на каждый кубик; б) силу f1,2, с которой второй кубик действует на первый.

2.22. Тело скользит вниз по наклонной плоскости, угол наклона которой α = 30°. В точке B скорость тела v1 = 0,14 м/с, а в точке С, которая находится ниже точки В, скорость тела v2 = 2,57 м/с. Коэффициент трения тела о плоскость μ = 0,1. Найти промежуток времени движения тела из точки В в точку С.

2.23. Небольшое тело пустили снизу вверх по наклонной плоскости, составляющей угол α = 30° с горизонтом, с начальной скоростью v0 = 10 м/с. Коэффициент трения скольжения μ = 0,1. Найти: а) скорость тела при его возвращении в исходную точку; б) высоту поднятия тела; в) промежуток времени, включающий время подъема и возвращения тела в исходную точку.

2.24. Два тела массами т1 = 0,8 кг и m2 = 1,5 кг связаны невесомой нерастяжимой нитью, переброшенной через невесомый блок, и находятся на наклонных плоскостях, образующих с горизонтом углы α = 15° и β = 30° (рис. 2.5). Коэффициент трения тел о плоскости одинаков и равен μ = 0,1. Найти ускорение, с которым движутся тела, и силу натяжения нити.

2.25. В установке, представленной на рис. 2.6, известны угол α наклонной плоскости с горизонтом и коэффициент трения μ между телом m1 и наклонной плоскостью. Массы блока и нити пренебрежимо малы, трения в блоке нет. Считая, что в начальный момент оба тела неподвижны, найти отношение масс т2/m1, при котором тело т2: а) начнет опускаться; б) начнет подниматься; в) будет оставаться в покое.

2.26. Через невесомый блок, подвешенный к пружинным весам, перекинута легкая нерастяжимая нить, к концам которой прикреплены грузы массами т1 =0,5 кг и т2 = 0,6 кг. Что покажут весы во время движения грузов, если пренебречь трением в оси блока?

2.27. Масса шарика 1 (рис, 2.7) в 1,5 раза меньше массы стержня 2, длина которого l = 1 м. Массы блока и нити, а также трение в оси пренебрежимо малы. Шарик установили на одном уровне с нижним концом стержня и отпустили. Найти промежуток времени, по прошествии которого шарик поравняется с верхним концом стержня.

2.28. Через невесомый блок перекинута легкая нерастяжимая нить, к одному концу которой подвешен груз 1 массой m1 = 0,5 кг (рис. 2.8). На другой конец нити действуют постоянной силой F = 7,5 Н. Пренебрегая трением в оси блока, найти, как изменится ускорение груза 1, если к другому концу нити подвесить груз 2, сила тяжести которого m2g = 7,5 Н. Трения в блоке нет.

2.29. К легкой нерастяжимой нити, перекинутой через невесомый блок, подвешены два груза 1 и 2, отношение масс которых т1/m2 = 3. Найти, какую часть составляет путь, пройденный грузом 1 за время τ от начала движения, от того расстояния, которое этот груз прошел бы при свободном падении за это же время.

2.30. На рис. 2.9 массы грузов m1 и m2 известны. Массы блоков и нитей, а также трение пренебрежимо малы. Найти ускорения а1 и а2 грузов и силу натяжения нити, к которой подвешен груз m1. Рассмотреть частные случаи: a) m1 = m2; б) 2m1 = m2.

2.31. Самолет делает "мертвую петлю" радиусом R = 500 м с постоянной скоростью v = 360 км/ч. Найти вес летчика, масса которого m — 70 кг, в нижней, верхней и средней точках петли.

2.32. Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Разность между максимальным и минимальным натяжениями веревки ΔFH = 9,8 Н. Найти массу камня.

2.33. Груз, привязанный к веревке длиной l = 0,5 м, равномерно вращается в вертикальной плоскости. Найти, при какой частоте вращения веревка разорвется, если известно, что она разрывается при натяжении, равном десятикратной силе тяжести груза.

2.34. Мотоциклист делает поворот на горизонтальной поверхности по дуге радиусом кривизны R = 80 м. Коэффициент трения колес о почву μ = 0,4. Найти: а) максимальную скорость, которую может развить мотоциклист на повороте; б) угол, на который он должен накрениться, чтобы не упасть.

2.35. 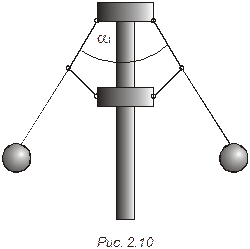По закруглению радиусом R = 480 м идет поезд с постоянной скоростью v = 75 км/ч. Под каким углом к горизонту надо расположить полотно железной дороги, чтобы избежать бокового давления колес на наружный рельс?

2.36. Центробежный регулятор совершает n1 оборотов в секунду. При этом между стержнями, несущими шары регулятора, образуется угол α1 = 30°. Во сколько раз надо увеличить число оборотов, чтобы стержни разошлись на угол α2 = 90 (рис.2.10)?

2.37. Мотоциклист с постоянной скоростью v = 20 м/с едет по окружности внутренней поверхности цилиндра, ось которого расположена вертикально. Радиус цилиндра R = 4 м. Найти коэффициент трения шин мотоцикла о стенки цилиндра. Размерами мотоцикла и человека пренебречь.

2.38. Тяжелый шарик, подвешенный на легкой нерастяжимой нити длиной l = 0,5 м, вращается в горизонтальной плоскости. Нить образует с вертикалью угол α = 30°. Найти период вращения шарика.

2.39. 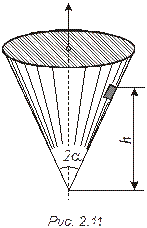На внутренней поверхности конической воронки с углом раствора 2α при вершине (рис. 2.11) находится малое тело на высоте h от вершины. Коэффициент трения между телом и поверхностью воронки равен μ. Найти минимальную угловую скорость вращения конуса вокруг вертикальной оси, при которой тело будет неподвижно в воронке.

2.40. К вращающемуся горизонтальному диску на расстоянии R = 10 см от оси вращения привязана легкая нерастяжимая нить длиной l = 0,6 м с грузиком на конце (рис. 2.12). При вращении нить образует угол α = 45° с вертикалью. На каком расстоянии R от оси вращения диска может удержаться небольшое тело, положенное на диск, если коэффициент трения тела о поверхность диска μ = 0,25?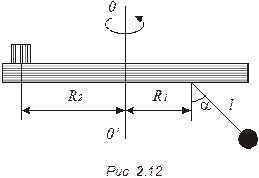

2.41. Молот массой т = 1,5 т падает с высоты h = 1,77 м на наковальню. Длительность удара Δt = 0,015 с. Найти среднее значение силы удара.

2.42. Комок мягкого снега массой т = 100 г брошен со скоростью v = 6 м/с под углом α = 45° к поверхности стены. При ударе снег прилипает к стене. Найти импульс силы, полученный стеной.

2.43. Струя воды сечением S = 5,6 см² ударяет о стенку под углом α = 60° к нормали и упруго отскакивает от нее без потери скорости. Скорость воды в струе v = 14 м/с. Найти среднее значение силы, действующей на стенку.

2.44. Молекула массой т = 4,65·10^-26 кг, летящая нормально к стенке сосуда со скоростью v = 600 м/с, ударяется о стенку и упруго отскакивает от нее. Найти импульс силы, полученный стенкой за время удара.

2.45. Молекула массой т = 4,65 10^-26 кг, летящая со скоростью v = 600 м/с, ударяется о стенку сосуда под углом α = 60° к нормали и под таким же углом упруго отскакивает от нее. Найти импульс силы, полученный стенкой за время удара.

2.46. Шарик массой т ударяется со скоростью v1 о вертикальную стену нормально к ней и отскакивает от стены в противоположном направлении со скоростью v2 (v2 < v1). Время соударения Δt. Найти среднее значение силы удара о стену.

2.47. Упругий шарик массой m ударяется о вертикальную стену в точке, находящейся на высоте h над землей, и отскакивает от нее в противоположном направлении без потери скорости. Найти, на каком расстоянии от стены упадет шарик на землю, если импульс силы, полученный стеной за время удара, равен FΔt.

2.48. Шарик массой т = 70 г ударяется о вертикальную стену нормально к ней и отскакивает в противоположном направлении с меньшей скоростью. За время соударения со стеной импульс шарика изменился на Δp = 2,1 Н·с. За промежуток времени τ = 1,5 с после удара о стену шарик упал на землю на расстоянии L = 2 м от нее. Найти скорость, с которой шарик подлетел к стене.

2.49. Шарик массой m = 0,1 кг, падая вертикально с некоторой высоты, ударяется о наклонную плоскость и упруго отскакивает от нее. Угол наклона плоскости к горизонту α = 30°. Импульс силы, полученный плоскостью за время удара, ΔF = 1,73 Н·с. Найти время, прошедшее от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории.

2.50. Теннисный мячик массой m падает на стол под углом α к поверхности стола и упруго отскакивает под таким же углом. Через время т он ударяется о стол на расстоянии L от точки первого удара. Найти импульс силы, полученный столом за один удар.

Задание 3. ЗАКОНЫ СОХРАНЕНИЯ