1. Исходя из основного закона динамики в форме dp / dt = F, получите уравнение моментов для материальной точки dL / dt = М. Дайте определение момента силы М и момента импульса L относительно: а) точки; б) оси вращения. Каковы свойства этих физических величин?
2. Покажите, что для системы материальных точек dL / dt = М, где 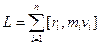 – момент импульса системы,
– момент импульса системы, 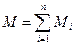 результирующий момент внешних сил.
результирующий момент внешних сил.
3. Сформулируйте закон сохранения момента импульса для системы материальных точек, указав на его связь с изотропностью пространства. Приведите примеры сохранения момента импульса.
4. Что называется центром масс абсолютно твердого тела? Запишите закон движения центра масс абсолютно твердого тела.
5. Получите уравнение моментов для материальной точки, движущейся по окружности, относительно оси вращения: Iβz = Mz. Чему равен момент инерции I материальной точки относительно оси вращения?
6. Запишите уравнение вращательного движения твердого тела вокруг неподвижной оси. Чему равен момент инерции I твердого тела относительно оси вращения? Является ли эта величина аддитивной?
7. Какие оси вращения твердого тела называются: свободными; главными? Каковы особенности вращения твердых тел вокруг свободных осей вращения?
8. Как вычисляются моменты инерции твердых тел относительно заданных осей вращения? Запишите и сформулируйте теорему Штейнера.
9. Дайте определение плоского движения твердого тела. Какими уравнениями описывается такое движение?
10. Запишите выражение для кинетической энергии твердого тела, вращающегося вокруг неподвижной оси. Чему равна кинетическая энергия твердого тела при плоском движении?
11. Как определить работу внешних сил при вращении твердого тела вокруг неподвижной оси?
12. Каковы специфические свойства гироскопов? Приведите примеры использования гироскопов. Какое движение гироскопа называется прецессией?
ЗАДАЧИ
4.1.Найти главные моменты инерции I1, I2, I3 плоского тонкого однородного кольца радиусом R и массой т.
4.2.Найти главные моменты инерции тонкого однородного диска радиусом R и массой т.
4.3.Вычислить момент инерции полого цилиндра массой т с внутренним и внешним радиусами R1 и R2 соответственно относительно оси, совпадающей с осью симметрии цилиндра.
4.4. 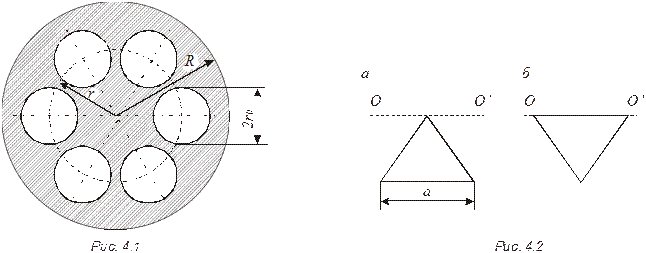 Медный диск радиусом R = 12 см и толщиной b = 0,1 см имеет шесть вырезов радиусом r0 = 3 см (рис. 4.1). Центры вырезов находятся на окружности, проведенной из центра диска радиусом r = 1 см, на равных расстояниях друг от друга. Найти момент инерции диска относительно оси, проходящей через центр диска перпендикулярно к его плоскости.
Медный диск радиусом R = 12 см и толщиной b = 0,1 см имеет шесть вырезов радиусом r0 = 3 см (рис. 4.1). Центры вырезов находятся на окружности, проведенной из центра диска радиусом r = 1 см, на равных расстояниях друг от друга. Найти момент инерции диска относительно оси, проходящей через центр диска перпендикулярно к его плоскости.
4.5.Найти момент инерции тонкого однородного стержня длиной l и массой т относительно перпендикулярной к стержню оси, проходящей: а) через центр масс стержня; б) через конец стержня.
4.6.Найти момент инерции тонкого однородного стержня длиной l и массой от относительно оси, проходящей через конец стержня и составляющей со стержнем угол α.
4.7. 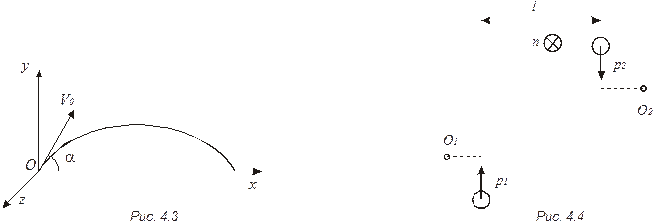 Найти момент инерции / проволочного равностороннего треугольника со стороной а = 0,3 м: а) относительно оси, лежащей в плоскости треугольника и проходящей через его вершину параллельно стороне, противоположной этой вершине; б) относительно оси, совпадающей с одной из сторон треугольника (рис. 4.2). Масса треугольника т = 54 г равномерно распределена по длине проволоки.
Найти момент инерции / проволочного равностороннего треугольника со стороной а = 0,3 м: а) относительно оси, лежащей в плоскости треугольника и проходящей через его вершину параллельно стороне, противоположной этой вершине; б) относительно оси, совпадающей с одной из сторон треугольника (рис. 4.2). Масса треугольника т = 54 г равномерно распределена по длине проволоки.
4.8.Найти момент инерции стальной прямоугольной пластины толщиной d — 0,1 см со сторонами а = 10 см и b = 20 см относительно оси, проходящей через центр масс пластины параллельно меньшей стороне.
4.9.Найти момент инерции прямого сплошного однородного конуса массой т и радиусом основания R относительно его оси симметрии.
4.10.Найти момент инерции сплошного однородного шара массой т и радиусом R относительно: а) оси симметрии; б) оси, проходящей через конец диаметра перпендикулярно к нему.
4.11.К точке, радиус-вектор которой относительно начала координат O равен r = аi + bj, приложена сила F = Аi + Вj, где а, b, А, В - постоянные. Найти момент М и плечо / силы F относительно точки О.
4.12.Сила F = 3i + 4j + 5k приложена к точке, радиус-вектор которой r = 4i + 2j + 3k. Найти: а) момент силы М относительно начала координат; б) модуль вектора М; в) момент силы Мz относительно оси z.
4.13.К точке с радиусом-вектором r = аi приложена сила F = Aj, а к точке с r2 = bj– сила F2 = Bi. Здесь оба радиуса-вектора определены относительно начала координат О; а, b, А и В – постоянные. Найти плечо равнодействующей силы относительно точки О.
4.14.Тело массой m = 1 кг брошено из точки, радиус-вектор которой r = 2j, вверх по вертикали с начальной скоростью v0 = 10 м/с. Найти приращение момента импульса ΔL относительно начала координат за все время полета тела (до возвращения его в исходную точку). Ось z направлена вверх. Сопротивлением воздуха пренебречь.
4.15.Тело массой т = 0,1 кг бросили с некоторой высоты в горизонтальном направлении со скоростью v0 = 20 м/с. Найти модуль приращения момента импульса тела относительно точки бросания за первые τ = 5 с. Сопротивлением воздуха пренебречь.
4.16.Тело массой т брошено с начальной скоростью v0, образующей угол α с горизонтом. Найти момент импульса L тела относительно точки бросания для момента времени, когда тело находится в верхней точке траектории. Сопротивлением воздуха пренебречь.
4.17.Частице массой т сообщена начальная скорость v0 под углом а к горизонту. Траектория полета частицы лежит в плоскости ху (рис. 4.3). Пренебрегая сопротивлением воздуха, найти зависимость от времени относительно точки бросания: а) момента М силы, действующей на частицу; б) момента импульса L частицы.
4.18.Две частицы движутся равномерно в противоположных направлениях вдоль параллельных прямых (рис. 4.4). Расстояние между прямыми l. Нормаль n к плоскости, в которой лежат траектории частиц, направлена за чертеж. Найти суммарные моменты импульса L1 и L2; частиц относительно точек O1 и О2, если импульсы частиц различны по модулю.
4.19.Решить задачу 4.18 для случая, когда модули импульсов частиц одинаковы: p1 = р2 = р3
4.20. 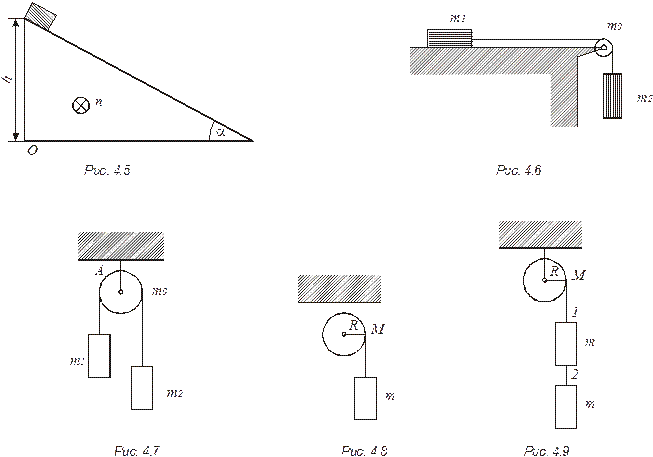 Материальная точка массой т начинает скользить без трения с вершины наклонной плоскости (рис. 4.5). Буквой n обозначена нормаль, направленная за чертеж. Найти относительно точки О: а) момент М результирующей силы, действующей на тело; б) момент импульса L тела.
Материальная точка массой т начинает скользить без трения с вершины наклонной плоскости (рис. 4.5). Буквой n обозначена нормаль, направленная за чертеж. Найти относительно точки О: а) момент М результирующей силы, действующей на тело; б) момент импульса L тела.
4.21.К ободу однородного диска радиусом R = 0,2 м приложена постоянная касательная сила F = 98,1 Н. При вращении на диск действует момент сил трения М = 4,9 Н·м. Найти массу диска, если он вращается с постоянным угловым ускорением β = 100 рад/с2.
4.22.К ободу колеса массой т = 50 кг, имеющего форму диска радиусом R = 0,5 м, приложена касательная сила F = 98,1 Н. Найти угловое ускорение колеса. Через какое время после начала действия силы колесо будет иметь скорость, соответствующую частоте вращения, п = 100 об/с?
4.23.Цилиндрический однородный вал массой т = 80 кг и радиусом R = 4 см вращается с частотой n = 9 об/с. В момент t = 0 к поверхности вала прижали тормозную колодку с силой F = 30 Н. Коэффициент трения колодки о вал μ = 0,31. Найти время, за которое вал остановится.
4.24.В системе, представленной на рис. 4.6, m1 = 1 кг, m2 = 1,2 кг, m0 = 0,6 кг. Коэффициент трения между телом т1 и горизонтальной поверхностью μ = 0,1. Блок m0 считать однородным диском, скольжения нити по блоку нет, трением в оси блока пренебречь. В момент t = 0 тело т2 начинает опускаться. Найти работу силы трения, действующей на тело m1 за первые τ = З с движения.
4.25.На рис. 4.7 т1 = 600 г, т2 = 450 г, m0 = 600 г. Блок считать однородным диском, трением в оси пренебречь. Учитывая, что нить не скользит по блоку, найти: а) ускорения грузов m1 и т2; б) силы натяжения нитей; в) усилие FA в подвеске.
4.26. 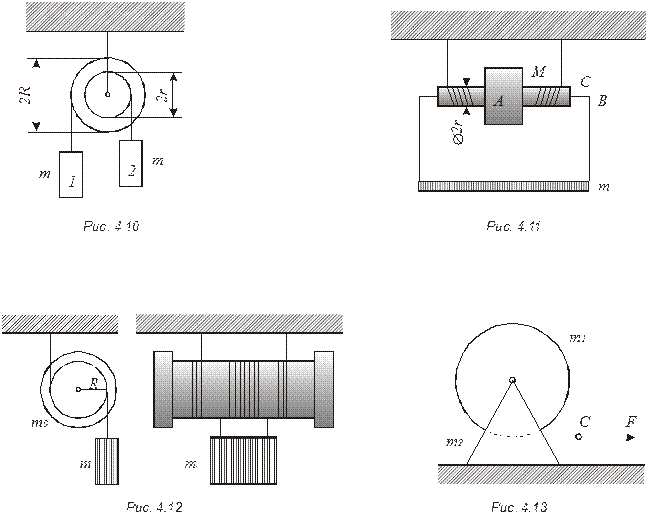 Однородный цилиндр массой М и радиусом R (рис. 4.8) вращается без трения вокруг горизонтальной оси под действием груза, прикрепленного к легкой нити, намотанной на цилиндр. Масса груза m. Найти угол φ поворота цилиндра в зависимости от времени, если при t = 0 угол φ0 = 0.
Однородный цилиндр массой М и радиусом R (рис. 4.8) вращается без трения вокруг горизонтальной оси под действием груза, прикрепленного к легкой нити, намотанной на цилиндр. Масса груза m. Найти угол φ поворота цилиндра в зависимости от времени, если при t = 0 угол φ0 = 0.
4.27.Однородный цилиндр массой М и радиусом R вращается без трения вокруг горизонтальной оси под действием двух грузов, подвешенных к легкой нити 1, намотанной на цилиндр, и связанных между собой легкой нитью 2 (рис. 4.9). Масса каждого груза т. Определить натяжение нити 2.
4.28.На ступенчатый вал (рис. 4.10), радиусы которого R = 0,2 м и r = 0,1 м намотаны в противоположных направлениях нити, нагруженные одинаковыми массами m = 1,0 кг. Момент инерции вала относительно его оси симметрии I = 2·10-2 кг·м2. Массой нитей и трением в оси блока пренебречь. Найти ускорения грузов 1 и 2.
4.29.Найти ускорение, с которым будет опускаться диск А (рис. 4.11), если к стержню В, без трения проходящему через отверстие внутри валика С, на нитях подвешено тело массой m. Масса диска и валика M, их момент инерции относительно оси стержня I, радиус валика r. Массой нитей и стержня пренебречь.
4.30.На рис. 4.12 масса груза m = 0,4 кг, масса катушки m0 = 0,8 кг, момент инерции катушки относительно ее оси симметрии I = 4,25·10-3 кг·м2. Найти ускорение, с которым опускается ось катушки, если ее радиус R =0,1 м. Массой нитей и трением в оси блока пренебречь.
4.31.Пуля массой т летит со скоростью v, вращаясь около продольной оси с частотой п. Принимая пулю за цилиндрик диаметром d, найти ее полную кинетическую энергию.
4.32.Кинетическая энергия вала, вращающегося вокруг неподвижной оси с постоянной скоростью, соответствующей частоте п = 5 об/с, равна WK = 60 Дж. Найти момент импульса вала.
4.33.Обруч и сплошной цилиндр, имеющие одинаковую массу т = 2,6 кг, катятся без скольжения с одинаковой скоростью v = 6 м/с. Найти кинетические энергии этих тел.
4.34.Обруч и диск, имеющие одинаковую массу, катятся без скольжения с одинаковой линейной скоростью. Кинетическая энергия обруча 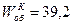 Дж. Найти кинетическую энергию диска.
Дж. Найти кинетическую энергию диска.
4.35.Шар катится по горизонтальной плоскости. Какую часть составляет энергия поступательного движения шара от его общей кинетической энергии?
4.36.С одного уровня наклонной плоскости одновременно начинают скатываться сплошные цилиндр и шар одинаковых радиусов. Какое тело будет иметь большую скорость на данном уровне и во сколько раз? Во сколько раз скорость одного тела будет больше скорости другого в данный момент времени?
4.37.Однородные сплошные шар и цилиндр, имеющие одинаковый радиус, двигаясь с одинаковой скоростью по горизонтальной плоскости, вкатываются вверх по наклонной плоскости. Найти отношение высот подъема этих тел.
4.38.Однородный диск радиусом R раскрутили до угловой скорости ω и осторожно положили на горизонтальную поверхность. Сколько времени диск будет вращаться на поверхности, если коэффициент трения равен μ? Давление диска на поверхность считать равномерным.
4.39.Сплошной однородный цилиндр массой т1 свободно вращается вокруг горизонтальной оси, укрепленной на подставке массой т2, которая находится на гладкой горизонтальной поверхности. На цилиндр плотно намотана невесомая нить, к концу которой приложили постоянную горизонтальную силу F. Найти кинетическую энергию системы через Δt секунд после начала движения (рис. 4.13).
4.40. 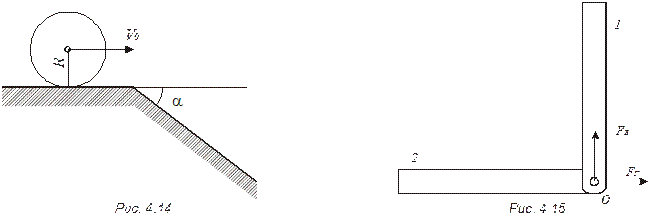 Сплошной однородный цилиндр радиусом R = 15 см катится без скольжения по горизонтальной плоскости, которая переходит в наклонную, составляющую угол α = 30° с горизонтом (рис. 4.14). Найти максимальную скорость v0, при которой цилиндр перейдет на наклонную плоскость еще без скачка.
Сплошной однородный цилиндр радиусом R = 15 см катится без скольжения по горизонтальной плоскости, которая переходит в наклонную, составляющую угол α = 30° с горизонтом (рис. 4.14). Найти максимальную скорость v0, при которой цилиндр перейдет на наклонную плоскость еще без скачка.
4.41.Карандаш, поставленный вертикально, падает на стол. Длина карандаша l = 15 см. Найти угловую и линейную скорости середины карандаша в конце падения.
4.42.На какой угол а надо отклонить тонкий однородный стержень длиной l = 1,2 м, подвешенный на горизонтальной оси, проходящей через верхний конец стержня, чтобы его нижний конец при прохождении положения равновесия имел скорость v = 4,9 м/с?
4.43.Тонкий однородный стержень длиной l висит на горизонтальной оси, проходящей через один из его концов. Найти начальную угловую скорость ω0, которую надо сообщить стержню, чтобы он отклонился от вертикали на угол α = 90°.
4.44.Однородный стержень массой т и длиной l падает без начальной скорости из положения 1, вращаясь без трения вокруг неподвижной горизонтальной оси О. Найти горизонтальную Fг и вертикальную Fв составляющие силы, с которой ось О действует на стержень в горизонтальном положении 2 (рис. 4.15).
4.45.Горизонтальная платформа в виде круглого однородного диска массой m = 80 кг и радиусом R = 1 м вращается с частотой п1 = 20 об/мин. В центре платформы стоит человек и держит в раскинутых руках гири. С какой частотой будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I1 = 2,94 кг·м2 до I2 = 0,98 кг·м2?
4.46.Платформа массой М в виде однородного диска может вращаться около вертикальной оси, проходящей через центр масс. По краю платформы начинает идти человек массой т и, обойдя ее, возвращается в исходную точку. Найти, на какой угол при этом повернется платформа. Человека можно принять за материальную точку.
4.47.Горизонтальная платформа в виде однородного диска радиусом R = 12 м вращается с частотой п1 = 4,5 об/мин. На краю платформы стоит человек массой т = 60 кг. С какой частотой будет вращаться платформа, если человек перейдет в ее центр? Момент инерции платформы I = 144 кг·м2; человека можно принять за материальную точку.
4.48.На скамье Жуковского стоит человек и держит в руке вертикальную ось вращающегося в горизонтальной плоскости велосипедного колеса. Ось колеса совпадает с осью скамьи. Угловая скорость вращения колеса ω1 = 12 рад/с, его момент инерции относительно этой же оси I = 0,4 кг·м2. Момент инерции человека и скамьи I0 = 3,2 кг·м2. Найти, с какой угловой скоростью начнет вращаться скамья, если повернуть колесо вокруг горизонтальной оси на угол α = 180°.
4.49.На неподвижной скамье Жуковского стоит человек и ловит мяч массой т = 250 г, летящий со скоростью v = 36 м/с в горизонтальном направлении на расстоянии r = 70 см от вертикальной оси вращения скамьи. После этого скамья стала поворачиваться с угловой скоростью ω = 0,9 рад/с. Найти момент инерции человека и скамьи.
4.50.Однородный стержень длиной l = 1,5 м и массой М = 10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня. В середину стержня попадает пуля массой m = 10 г, летящая в горизонтальном направлении перпендикулярно к оси вращения со скоростью v = 500 м/с. Считая удар абсолютно неупругим, найти угол, на который отклонится стержень после удара.
Задание 5. ГРАВИТАЦИОННОЕ ПОЛЕ. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА
 2015-02-14
2015-02-14 3707
3707
