Вопросы и упражнения. 1. В чем заключается механический принцип относительности

1.В чем заключается механический принцип относительности? В чем состоит ограниченность этого принципа?

2.Как записываются преобразования Галилея? Каким образом вводятся понятия движущейся К' (штрихованной) и неподвижной К (лабораторной) систем отсчета?

3.На основе преобразований Галилея; а) укажите относительные и инвариантные свойства пространства и времени; б) сравните показания движущихся и неподвижных часов; длины движущейся и неподвижной линейки. Получите правило сложения скоростей в классической механике.

4.Покажите связь закона инерции с принципом относительности Галилея. Какие величины ньютоновской динамики инвариантны?

5.Сформулируйте постулаты специальной теории относительности (СТО) Эйнштейна. В чем отличие первого постулата СТО от принципа относительности в механике? Отличаются ли постулаты об общих свойствах пространства и времени в СТО от соответствующих классических?

6.В чем заключается проблема одновременности в релятивистской физике? Как в СТО вводится понятие "синхронизированные часы"?

7.Как в СТО определяется "длина движущегося тела"? Что называется: собственной длиной; лоренцевым сокращением?

8.Запишите преобразования Лоренца. Покажите, что преобразования Галилея являются частным случаем преобразований Лоренца.

9.Рассмотрите следствия из преобразований Лоренца: относительность одновременности, сокращение масштаба, замедление времени. Что называется пространственноподобным, времениподобным и светоподобным интервалами?

10.Получите на основе преобразований Лоренца релятивистский закон сложения скоростей.

11.Запишите релятивистское выражение: а) для массы; б) для импульса; в) для кинетической энергии. Каковы особенности основного уравнения релятивистской динамики?

12.Каково содержание закона Е = mс² (с – скорость света в вакууме)?

ЗАДАЧИ

6.1.При какой скорости движения релятивистское сокращение длины движущегося тела составляет 25 %?

6.2.Отношение сторон прямоугольника а/b = 2/1. С какой скоростью (в долях скорости света) и в каком направлении должен двигаться прямоугольник, чтобы "неподвижному" наблюдателю он казался квадратом?

6.3.Суммарная поверхность неподвижного тела, имеющего форму куба, равна S0. Чему равна поверхность S того же тела, если оно движется в направлении одного из своих ребер со скоростью v = 0,968с?

6.4.Найти собственную длину стержня, если в лабораторной системе отсчета его скорость v = с/2, длина l = 1,00 м и угол между ним и направлением движения θ = 45°.

6.5.Стержень, собственная длина которого l0 = 1,00 м, движется в системе К со скоростью v = 0,75 с. Угол между стержнем и направлением движения θ = 30°. Найти длину стержня в системе К'.

6.6.Скорость мезонов космических лучей, достигающих поверхности Земли, различна. Найти релятивистское сокращение размеров мезона, имеющего скорость v = 0,95 с.

6.7.С какой скоростью двигались в K-системе отсчета часы, если за время τ = 5,0 с (в K'-системе) они отстали от часов этой системы на Δt = 0,1 с?

6.8.На космическом корабле-спутнике находятся часы, синхронизированные до полета с земными. Скорость спутника v0 = 7,9 км/с. Насколько отстанут часы на спутнике по сравнению с часами земного наблюдателя за время Δτ0 = 0,5 года?

6.9.Фотонная ракета движется относительно Земли со скоростью v = 0,6 с. Во сколько раз замедлится ход времени в ракете с точки зрения земного наблюдателя?

6.10. 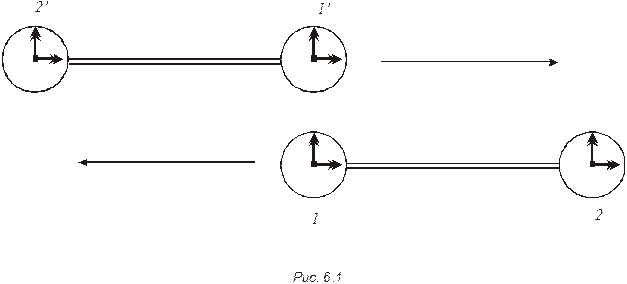На концах двух стержней собственной длиной l0 = 10,0 м укреплены одинаковые синхронизированные друг с другом часы (рис. 6.1). Стержни приведены в движение с относительной скоростью v = с/2. В момент, когда часы 1 и 1' находятся друг против друга, стрелки обоих часов показывают нулевой отсчет. Определить: а) показания часов 1 и 2' в момент, когда они поравняются друг с другом; б) показания часов 2 и 1' в момент, когда они поравняются друг с другом; в) показания часов 2 и 2' в момент, когда они поравняются друг с другом.

6.11.Пусть в К-системе отсчета два события совершаются на расстоянии Δх = 6·10⁵ км друг от друга с промежутком времени Δt = 1 с. С какой скоростью должен лететь космический корабль, чтобы в его системе отсчета эти события стали одновременными?

6.12.Два события в К-системе отсчета совершаются на расстоянии Δx = 3·10⁶ км с промежутком времени Δ = 15 с. Определить скорость космического корабля, при которой в его системе отсчета события будут одноместными.

6.13.С точки зрения наблюдателя, находящегося в движущемся поезде, удары молнии в точке А (впереди поезда) и в точке В (позади поезда) произошли одновременно. Какая молния с позиций СТО ударила в землю раньше для наблюдателя, находящегося на Земле?

6.14.По одной прямой движутся две частицы с одинаковыми скоростями v = 0,75с. Промежуток времени между ударами частиц в мишень оказался Δt = 1 нc. Каково расстояние между частицами в полете относительно К и К' систем отсчета?

6.15.Ракета движется относительно неподвижного наблюдателя, находящегося на Земле, со скоростью v = 0,99 с. Найти, как изменятся линейные размеры тел в ракете по линии движения для неподвижного наблюдателя. Какое время пройдет по часам неподвижного наблюдателя, если по часам, движущимся вместе с ракетой, прошел один год?

6.16.Космический корабль с постоянной скоростью v = 0,96с движется по направлению к центру Земли. Какое расстояние в системе отсчета, связанной с Землей, пройдет корабль за промежуток времени Δt' = 7 с, отсчитанный по корабельным часам? Вращение Земли и ее орбитальное движение не учитывать.

6.17.В K-системе отсчета пи-мезон с момента рождения до момента распада пролетел расстояние l = 75 м. Скорость пи-мезона v = 0,995 с. Определить собственное время жизни частицы.

6.18.Собственное время жизни некоторой частицы τ = 1,0·10^-6 с. Чему равен интервал Δs между рождением и распадом этой частицы?

6.19.С какой скоростью должна лететь частица относительно K-системы отсчета, чтобы промежуток собственного времени Δτ был в 10 раз меньше промежутка Δt, отсчитанного по часам К-системы?

6.20.За промежуток времени Δt = 1,0 с, измеренный по часам некоторой К-системы отсчета, частица, двигаясь прямолинейно и равномерно, переместилась из начала координат K-системы в точку с координатами х = у = z =1,5·10⁸ м. Найти промежуток собственного времени частицы, за который произошло это перемещение.

6.21.Две ракеты движутся навстречу друг другу со скоростями v1 = v2 = 0,75 с по отношению к неподвижному наблюдателю. Найти скорость сближения ракет согласно релятивистскому закону сложения скоростей.

6.22.Две частицы движутся навстречу друг другу со скоростями v1 = 0,5 с и v2 = 0,75 с по отношению к К-системе отсчета. Найти относительную скорость частиц.

6.23.Две релятивистские частицы движутся в К-системе отсчета со скоростями v1 = 0,6 с и v2 = 0,9 с вдоль одной прямой. Определить относительную скорость частиц в двух случаях: а) частицы движутся в одном направлении; б) частицы движутся в противоположных направлениях.

6.24.Две релятивистские частицы движутся под прямым углом друг к другу в K-системе отсчета, причем одна — со скоростью v1, другая — со скоростью v2. Найти их относительную скорость.

6.25.Ион, вылетев из ускорителя, испустил фотон в направлении своего движения. Определить скорость фотона относительно ускорителя, если скорость иона относительно ускорителя v = 0,8 с.

6.26.На ракете, летящей со скоростью v = 0,9 с, установлен ускоритель, сообщающий частицам скорость v' = 0,8 с относительно ракеты (по направлению ее движения). Найти скорость частиц в системе отсчета, связанной с "неподвижными" звездами. Решить также задачу для случая, когда частицы движутся в противоположную движению ракеты сторону.

6.27.Ускоритель сообщил радиоактивному ядру скорость v1 = 0,4 с. В момент вылета из ускорителя ядро выбросило в направлении своего движения (3-частицу со скоростью и = 0,75с относительно ускорителя. Найти скорость частицы относительно ядра.

6.28.Два ускорителя выбрасывают навстречу друг другу частицы с одинаковыми по модулю скоростями v = 0,9 с относительно ускорителя. Определить относительную скорость частиц.

6.29.В плоскости ху K-системы отсчета движется частица, проекции скорости которой равны vx и vy. Найти скорость v' этой частицы в K'-системе, которая перемещается со скоростью u относительно K-системы в положительном направлении ее оси х.

6.30.K'-система отсчета движется относительно К-системы со скоростью v0 = 0,50с. Скорость некоторой частицы в K'-системе v' = 0,1732 (i' + j' + k'). Найти скорость v частицы в К-системе, модуль v этой скорости и угол α, образуемый v с осью х.

6.31.Какова скорость электрона, масса которого превышает его массу покоя в 4·10⁴ раз?

6.32.При какой скорости масса движущегося электрона вдвое больше его массы покоя?

6.33.Отношение заряда движущегося электрона к его массе, определенное из опыта, q/m = 0,88·10¹¹ Кл/кг. Определить релятивистскую массу электрона и его скорость.

6.34.С какой скоростью должен лететь протон (m0 = 1 а.е.м.), чтобы его масса равнялась массе покоя α-частицы (mα = 4 а.е.м.)?

6.35.Насколько увеличивается масса α-частицы при ускорении ее от начальной скорости v0 = 0 до скорости v = 0,9 с?

6.36.Найти скорость релятивистской частицы массой m = 0,911·10 ^-30 кг (масса электрона), импульс которой p = 1,58·10^-22 кг·м/с.

6.37.Сравнить модули релятивистского и ньютоновского импульсов электрона при скорости v = 0,96 с.

6.38.Найти скорость, при которой релятивистский импульс частицы в два раза превышает ее ньютоновский импульс.

6.39.Протон движется с импульсом р = 10,0 ГэВ/с,где с – скорость света. Какой процент составляет отличие скорости протона от скорости света?

6.40.Плотность покоящегося тела ρ0. Найти скорость системы отсчета относительно данного тела, в которой его плотность будет на 25 % больше p0.

6.41.До какой энергии можно ускорить частицы в циклотроне, если относительное увеличение массы частиц не должно превышать 5 %? Задачу решить для электронов и протонов.

6.42.Выразить в мегаэлектронвольтах энергию покоя: а) электрона; б) протона.

6.43.Определить уменьшение массы Солнца за один год, если известно, что общая мощность излучения Солнца составляет около Р = 3,8·10²⁶ Вт.

6.44.Выразить релятивистский импульс частицы, масса которой равна т,через ее релятивистскую кинетическую энергию.

6.45.Какая относительная ошибка будет допущена при вычислении кинетической энергии релятивистской частицы, если вместо релятивистского, выражения Wp = (m - m1) c² воспользоваться классическим Wкл = m0v²/2? Вычисления выполнить для двух случаев: а)v = 0,2 с; б) v = 0,8 с.

6.46.Импульс релятивистской частицы р = m0c. Под действием внешней силы импульс частицы увеличился в два раза. Во сколько раз возрастет при этом энергия частицы: а) кинетическая; б) полная?

6.47.На покоящуюся частицу массой т 1 налетает частица массой т2, кинетическая энергия которой W^K. После столкновения частицы слипаются и движутся как целое. Найти массу образовавшейся частицы. Чему равна ее скорость?

6.48.Какова должна быть кинетическая энергия протона, налетающего на другой, покоящийся протон, чтобы их суммарная кинетическая энергия в системе центра инерции была такая же, как у двух протонов, движущихся навстречу друг другу с кинетическими энергиями W^K = 25 ГэВ?

6.49.Найти длину пробега релятивистской заряженной частицы с зарядом е и массой m при начальной полной энергии E0 в тормозящем однородном электрическом поле, параллельном начальной скорости частицы.

6.50.Получить основное уравнение релятивистской динамики для случаев: a) 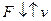; 6) .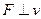

Задание 7. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ