1.Какими фундаментальными свойствами пространства и времени обусловлены законы сохранения?
2.Какие силы называются: внешними; внутренними? Какие системы материальных точек называются: замкнутыми; незамкнутыми? Может ли система вести себя как замкнутая в одном определенном направлении?
3.Покажите, что для системы материальных точек 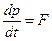 , где
, где 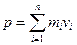 – импульс системы;
– импульс системы; 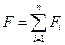 результирующая всех внешних сил. Что называется центром масс системы материальных точек и каковы его свойства?
результирующая всех внешних сил. Что называется центром масс системы материальных точек и каковы его свойства?
4.Сформулируйте закон сохранения импульса для системы материальных точек, указав на его связь с однородностью пространства. Приведите примеры проявления закона сохранения импульса, сохранения проекции импульса.
5.Запишите уравнение динамики тела с переменной массой (уравнение Мещерского) и поясните смысл входящих в него величин.
6.Дайте определение: а) механической работы А; б) мощности N. Каковы свойства этих физических величин? В каких единицах они измеряются?
7.Какие силы называются: консервативными; не консервативными? Какие поля являются: потенциальными; непотенциальными?
8.Получите выражение для кинетической энергии движущейся материальной точки. Выведите формулу для потенциальной энергии: а) тела, поднятого над землей; б) упруго деформированной пружины.
9.Для каких систем тел справедлив закон сохранения механической энергии и как он формулируется? Укажите на его связь с однородностью времени.
10.Какое взаимодействие называется ударом? Приведите примеры абсолютно упругого и неупругого ударов.
11.Какими законами сохранения определяется соотношение между начальным и конечным состоянием тел, участвующих в соударении? В какие виды энергии может переходить кинетическая энергия соударяющихся тел? Позволяют ли законы сохранения определить, что происходит в процессе соударения?
12.Используя законы динамики и закон сохранения энергии, получите уравнение Бернулли для идеальной несжимаемой жидкости.
ЗАДАЧИ
3.1.Льдина площадью поперечного сечения S и высотой H плавает в воде. Найти работу, которую надо совершить, чтобы льдину полностью погрузить в воду. Плотность льда ρл и плотность воды ρв известны.
3.2.Шар радиусом R = 6 см удерживается внешней силой под водой так, что его верхняя точка касается поверхности воды. Плотность материала шара ρ = 500 кг/м3. Какую работу совершит выталкивающая сила, если отпустить шар и предоставить ему свободно всплывать?
3.3.Из залитого подвала, площадь пола которого S = 50 м2, требуется выкачать воду на мостовую. Глубина воды в подвале h = 1,5 м, а расстояние от уровня воды в подвале до мостовой Н = 5 м. Найти работу, которую надо совершить при откачке воды.
3.4.Однородная цепочка длиной l = 1,2 м и массой т = 2,8 кг лежит на столе. Когда часть цепочки длиной l1 = 0,14 м спускают со стола, она начинает скользить. Коэффициент трения между столом и цепочкой l = 0,1. Найти работу по преодолению силы трения, совершаемую при соскальзывании всей цепочки.
3.5.Однородная цепочка длиной l лежит на горизонтальной плоскости так, что 1/3 ее длины находится на гладкой поверхности, а остальная – на шероховатой. Под действием постоянной горизонтальной силы F цепочку перетягивают с шероховатой поверхности на гладкую. Сила F равна минимальной силе, при которой цепочка начинает скользить; сила трения не зависит от скорости. Какую работу совершит сила трения, действующая на цепочку, при ее полном перемещении на гладкую поверхность?
3.6.Тело массой m бросили под углом α к горизонту с начальной скоростью v0. Найти среднюю мощность, развиваемую силой тяжести за все время движения тела, и мгновенную мощность этой силы как функцию времени.
3.7.Тело массой т под действием постоянной силы движется прямолинейно, причем зависимость координаты х тела от времени определяется равенством х = В + Ct + Dt2, где В, С, D - постоянные. Найти работу силы за интервал времени от 0 до 11.
3.8.Материальная точка массой т = 2 кг под действием постоянной силы тяги движется прямолинейно согласно уравнению х = Bt + Ct2 + Dt3, где В = -2 м/с, С = 1 м/с2, D = -0,2 м/с3. Найти мощность, развиваемую при движении точки в моменты t1 = 2 с и t2 = 5 с.
3.9.Частица совершила перемещение по некоторой траектории в плоскости ху из точки 1 с радиусом-вектором r1 = li + 2j в точку 2 с радиусом-вектором r2 = 2i - 3j под действием силы F = 3i + 4j. Найти работу, совершенную силой F на этом перемещении.
3.10.Тело массой т начинают поднимать с поверхности земли, приложив к нему силу, которую изменяют с высотой подъема у по закону F = 2(ау - 1)mg, где а - положительная постоянная. Найти работу этой силы на первой половине пути подъема.
3.11.Шарику, подвешенному на легкой нерастяжимой нити длиной l = 1 м, толчком сообщили скорость v = 6 м/с. Найти высоту, на которой нить ослабнет и шарик перестанет двигаться по окружности. Чему будет равна скорость шарика в этот момент?
3.12. 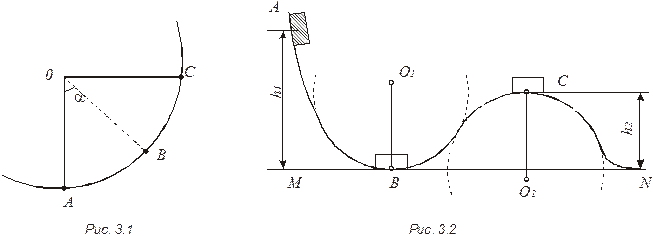 Груз массой т = 300 г подвешен на нити длиной l = 1 м, закрепленной в точке О (рис. 3.1). Нить отвели в сторону так, что она заняла горизонтальное положение, и отпустили. Найти силу натяжения нити в моменты прохождения грузом точек В и А, если угол α = 45°.
Груз массой т = 300 г подвешен на нити длиной l = 1 м, закрепленной в точке О (рис. 3.1). Нить отвели в сторону так, что она заняла горизонтальное положение, и отпустили. Найти силу натяжения нити в моменты прохождения грузом точек В и А, если угол α = 45°.
3.13.Небольшое тело массой т = 2 г соскальзывает без трения по искривленной поверхности из точки А (рис. 3.2). Точка А находится на высоте h1 = 50 см, а точка С – на высоте h2 = 30 см от горизонтальной плоскости MN. Радиусы кривизны поверхности в точках В и С одинаковы: R = 40 см. Найти модули сил давления на поверхность в точках В и С.
3.14.Тело массой т пустили вверх по наклонной плоскости, составляющей угол α с горизонтом. Начальная скорость тела v0, коэффициент трения μ. Найти: а) путь, пройденный телом до остановки; б) работу силы трения на этом пути.
3.15.  Небольшое тело начинает скользить с высоты h по наклонному желобу, переходящему в полуокружность радиусом R = h/2 (рис. 3.3). Пренебрегая трением, найти скорость тела в наивысшей точке его траектории (после отрыва от желоба).
Небольшое тело начинает скользить с высоты h по наклонному желобу, переходящему в полуокружность радиусом R = h/2 (рис. 3.3). Пренебрегая трением, найти скорость тела в наивысшей точке его траектории (после отрыва от желоба).
3.16.Небольшая шайба соскальзывает без начальной скорости с вершины гладкой горки высотой Н, имеющей горизонтальный трамплин (рис. 3.4). При какой высоте h трамплина шайба пролетит наибольшее расстояние L? Чему оно равно?
3.17.Гирька массой т = 0,5 кг, привязанная к резиновому шнуру длиной l0, описывает в горизонтальной плоскости окружность. Скорость движения гирьки соответствует частоте вращения п = 2 об/с. Угол отклонения резинового шнура от вертикали α = 30°. Найти длину нерастянутого резинового шнура. Для растяжения шнура на х1 = 1 см требуется сила F = 6 Н.
3.18.Тело массой т = 500 г, прикрепленное к резиновому шнуру длиной l0 = 9,5 см, отклоняют на угол α = 90° и отпускают. Коэффициент жесткости резинового шнура k = 9,8 Н/см. Найти длину l резинового шнура в момент прохождения телом положения равновесия.
3.19.Груз, положенный на чашку весов, сжимает пружину на х1 = 5 см. Найти величину сжатия пружины для случая, когда этот же груз падает на чашку весов с высоты h = 10 см.
3.20.Система состоит из двух последовательно соединенных пружинок с коэффициентами жесткости k1 и k2. Найти минимальную работу, которую необходимо совершить, чтобы растянуть эту систему на Δl.
3.21.Снаряд, летевший горизонтально со скоростью v = 100 м/с, разрывается на две равные части на высоте h = 40 м. Одна часть через τ = 1 с падает на землю точно под местом взрыва. Найти модуль и направление скорости второй части снаряда сразу после взрыва.
3.22.Определить, во сколько раз уменьшилась масса ракеты, если через некоторое время после запуска ее скорость составляла 57,5 м/с, а относительная скорость выхода продуктов сгорания из сопла и = 25 м/с. Сопротивлением воздуха и ускорением свободного падения пренебречь.
3.23.Начальная масса ракеты m0 = 200 г, масса заряда т = 180 г, начальная скорость ракеты равна нулю, относительная скорость выхода продуктов сгорания из сопла и = 30 м/с. Пренебрегая сопротивлением воздуха и ускорением свободного падения, найти скорость ракеты в момент полного выгорания заряда.
3.24.В баллистический маятник массой М = 4 кг попадает пуля массой т = 10 г, летящая с горизонтальной скоростью v = 400 м/с, и застревает в нем. Найти высоту, на которую поднимется, отклонившись, маятник, и долю кинетической энергии 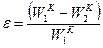 пули, израсходованной на пробивание маятника.
пули, израсходованной на пробивание маятника.
3.25.Навстречу друг другу летят два шара массами m1 и m2. Кинетическая энергия второго шара в 20 раз больше кинетической энергии первого. Между шарами происходит абсолютно неупругий удар. Найти, при каком соотношении m1\m2 шары после удара будут двигаться в сторону движения первого шара.
3.26.Частица массой m1 = 1 г, двигавшаяся со скоростью v1 = 3i — 2j, испытала абсолютно неупругое столкновение с другой частицей, масса которой m2 = 2 г и скорость v2 = 4i - 6j. Найти скорость u образовавшейся частицы.
3.27.Частица 1, двигавшаяся со скоростью v1 = 3i + 4j, испытала абсолютно неупругое соударение с частицей 2, скорость которой v2 = i + 2j. Скорость образовавшейся частицы оказалась равной u = 2i + 3j. Найти отношение масс m1/m2 частиц до соударения.
3.28.Частицы 1 и 2, отношение масс которых т1/т2 = 1/2, двигаясь в плоскости ху, испытали абсолютно неупругое столкновение. Радиусы-векторы частиц до соударения изменялись с течением времени по законам: r1 = 3ti +4tj; r2 = ti + 2tj. Найти скорость и образовавшейся частицы.
3.29.Частица 1 массой т, летящая со скоростью v, столкнувшись с неподвижной частицей 2 массой М, отскакивает от нее и летит в противоположном направлении со скоростью и1 = v/2. Найти: а) скорость частицы 2 после столкновения; б) энергию, которая пошла на нагревание и деформацию.
3.30.Частица 1 массой т, летящая со скоростью v, сталкивается с неподвижной частицей 2 массой 4m. После соударения частица 1 движется в противоположном направлении, а 1/4 часть ее первоначальной энергии уходит на нагревание и деформацию. Найти скорости и1 и u2 частиц после соударения.
3.31.Атом гелия массой т и атом пара ртути массой 50т движутся в вакууме по прямой навстречу друг другу. Скорость атома гелия 1·103 м/с, скорость атома ртути 2·102 м/с. Найти скорости и1 и и2 атомов после их соударения, считая удар упругим.
3.32.Нейтрон массой т ударяется о неподвижное ядро: а) атома углерода (mс = 12m); б) атома урана (mU = 235m). Считая удар центральным и упругим, найти, какую часть своей скорости ε = Δv/v потеряет нейтрон при ударе в каждом случае.
3.33.Во сколько раз уменьшится скорость атома гелия после упругого столкновения с неподвижным атомом водорода, масса которого в 4 раза меньше массы атома гелия?
3.34.Движущееся тело массой m1 ударяется о неподвижное тело массой m. Считая удар упругим и центральным, найти, какую часть первоначальной кинетической энергии первое тело передает второму при ударе. Задачу решить в общем виде, а затем рассмотреть случаи: а) m1 = т2, б) m1 = 9т2.
3.35.Какую максимальную часть 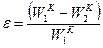 своей кинетической энергии может передать шарик массой m1 = 20 г, сталкиваясь упруго с неподвижным шариком массой т2 = 80 г?
своей кинетической энергии может передать шарик массой m1 = 20 г, сталкиваясь упруго с неподвижным шариком массой т2 = 80 г?
3.36.Частица 1 испытала абсолютно упругое столкновение с покоившейся частицей 2. Найти отношение их масс т1/m2, если: а) столкновение лобовое и частицы разлетелись в противоположных направлениях с одинаковыми скоростями; б) частицы разлетелись симметрично по отношению к первоначальному направлению движения частицы 1 и угол между их направлениями разлета Θ = 60.
3.37.На покоящийся шар налетает другой шар такой же массой, скорость которого v = 6 м/с. В результате упругого столкновения шар изменил направление своего движения на угол α = 30°. Найти скорости шаров после удара и угол β между вектором скорости второго шара и первоначальным направлением движения первого шара.
3.38.Частица 1 массой т1 с импульсом p1 налетает на покоящуюся частицу 2 массой т2 и испытывает с ней упругое столкновение. Найти импульсы 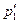 и
и 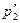 частиц после столкновения, в результате которого частица 2 отлетает под углом Θ к первоначальному направлению налетающей частицы 1.
частиц после столкновения, в результате которого частица 2 отлетает под углом Θ к первоначальному направлению налетающей частицы 1.
3.39.Маятник представляет собой легкий тонкий стержень длиной l = 1,5 м, на конце которого находится стальной шар массой М = 1 кг. В шар попадает летящий горизонтально со скоростью v = 50 м/с стальной шарик массой m = 20 г. Определить угол максимального отклонения маятника, считая удар упругим и центральным.
3.40.Два шара подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Масса первого шара т1 = 0,2 кг, второго – т2 = 0,1 кг. Первый шар отклоняют так, что его центр масс поднимается на высоту h = 4,5 см, и отпускают. На какую высоту поднимется каждый из шаров после соударения, если удар абсолютно упругий?
3.41.
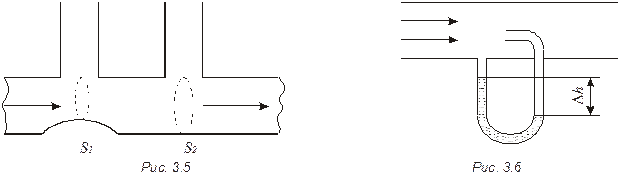 Две манометрические трубки установлены на горизонтальной трубе переменного сечения в местах, где сечения трубы равны S1 и S2 (рис. 3.5). По трубе течет вода. Найти объем воды, протекающей в единицу времени через сечение трубы, если разность уровней воды в манометрических трубках равна Δh.
Две манометрические трубки установлены на горизонтальной трубе переменного сечения в местах, где сечения трубы равны S1 и S2 (рис. 3.5). По трубе течет вода. Найти объем воды, протекающей в единицу времени через сечение трубы, если разность уровней воды в манометрических трубках равна Δh.
3.42. 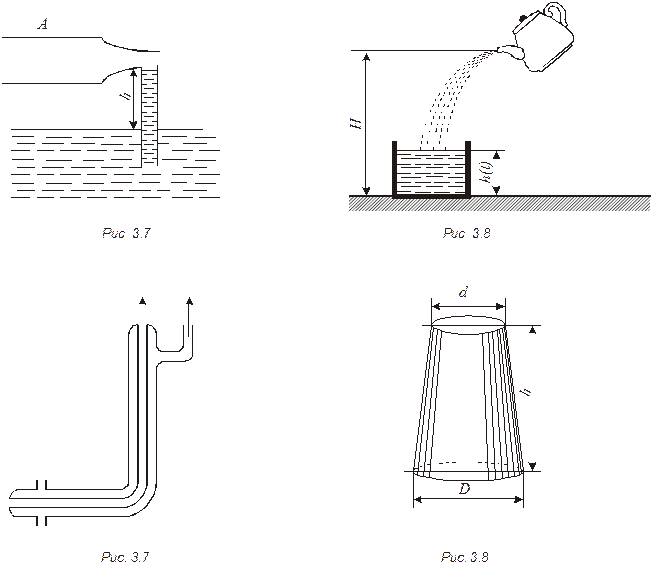 Трубка Пито (рис. 3.6) установлена по оси газопровода, площадь внутреннего сечения которого равна S. Пренебрегая вязкостью, найти объем газа, проходящего через сечение трубы в единицу времени, если разность уровней в жидкостном манометре равна Δh, а плотности жидкости и газа – соответственно ρ0 и ρ.
Трубка Пито (рис. 3.6) установлена по оси газопровода, площадь внутреннего сечения которого равна S. Пренебрегая вязкостью, найти объем газа, проходящего через сечение трубы в единицу времени, если разность уровней в жидкостном манометре равна Δh, а плотности жидкости и газа – соответственно ρ0 и ρ.
3.43.Схема устройства пульверизатора изображена на рис. 3.7. Определить максимальную высоту hmах, на которую он может засасывать жидкость плотностью ρ из резервуара, если давление перед входом в трубку А, где скорость очень мала, равно p0. Вязкостью пренебречь.
3.44.Найти зависимость от времени силы F, действующей на дно цилиндрического стакана площадью S, в который наливают воду из чайника (рис. 3.8). Известно, что за секунду в стакан наливается постоянное количество Q воды.
3.45.Шприц, применяемый для смазывания шарнирных соединений автомобиля, заполнили для промывки керосином. Радиус поршня шприца R = 2 см, ход поршня l = 25 см. Радиус выходного отверстия шприца r = 2 мм. Пренебрегая вязкостью керосина и трением поршня о стенки, определить время τ, за которое будет вытеснен керосин из шприца, если давить на поршень с постоянной силой F = 5 Н.
3.46.Какое давление р создает компрессор в краскопульте, если струя жидкой краски вытекает из него со скоростью v = 25 м/с? Плотность краски равна 0,8·103 кг/м3.
3.47.Устройство, называемое трубкой Пито-Прандтля, состоит из двух узких коаксиальных трубок (рис. 3.9). Внутренняя трубка открыта на нижнем конце, внешняя имеет боковые отверстия. Верхние концы трубок подключены к дифференциальному манометру, измеряющему разность давлений Δр. С помощью этого устройства можно измерять скорость жидкости (или газа). Для этого его погружают в жидкость, обратив открытым концом навстречу потоку, и отсчитывают Δр. При погружении трубки Пито-Прандтля в поток жидкости с плотностью р = 1,10·102 кг/м3 была обнаружена разность давлений Δр = 4,95·103 Па. Найти скорость v течения жидкости.
3.48.Сопло фонтана, дающего вертикальную струю высотой H, имеет форму усеченного конуса, сужающегося вверх (рис. 3.10). Диаметр нижнего сечения D, верхнего d, высота сопла h. Определить секундный расход V1 воды, подаваемой фонтаном, и избыточное давление Δр в нижнем сечении. Сопротивлением воздуха в струе и сопротивлением в сопле пренебречь.
3.49. 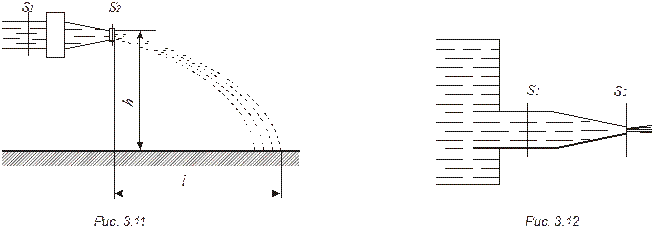 Струя воды площадью поперечного сечения S1 вытекает в горизонтальном направлении из брандспойта, расположенного на высоте h над поверхностью земли, и падает на эту поверхность на расстоянии l (рис. 3.11). Пренебрегая сопротивлением воздуха движению воды, определить избыточное давление Δр воды в рукаве, если площадь его поперечного сечения S2.
Струя воды площадью поперечного сечения S1 вытекает в горизонтальном направлении из брандспойта, расположенного на высоте h над поверхностью земли, и падает на эту поверхность на расстоянии l (рис. 3.11). Пренебрегая сопротивлением воздуха движению воды, определить избыточное давление Δр воды в рукаве, если площадь его поперечного сечения S2.
3.50.В боковой стенке широкого открытого бака вмонтирована суживающаяся трубка (рис. 3.12), через которую вытекает вода. Площадь сечения трубки уменьшается от S1 = 3,6 см2 до S2 = 1,2 см2. Уровень воды в баке на 4,9 м выше уровня в трубке. Пренебрегая вязкостью воды, найти горизонтальную составляющую силы F, действующую на трубку.
Задание 4. ДИНАМИКА ТВЕРДОГО ТЕЛА
 2015-02-14
2015-02-14 3205
3205
