Этап: формирование и решение задач с дополнительными ограничениями

В результате на основе исходной задачи с ослабленными ограничениями получают две самостоятельные задачи, отличающиеся от нее следующими дополнительными ограничениями:

1) 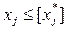; 2) .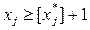

Решая полученные задачи, определяем их оптимальные решения.

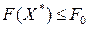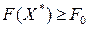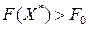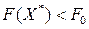Если в результате решения какой-либо задачи получен нецелочисленный оптимальный план, для которого (или в случае минимизации целевой функции), то данная задача исключается из списка. Если (или в случае минимизации целевой функции), то из данной задачи формируются новые две задачи в соответствии с этапами 2-3.

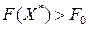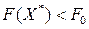Если полученное решение X^* удовлетворяет условию целочисленности и (или в случае минимизации целевой функции), то F ₀ присваивается оптимальное значение данной задачи 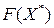, т.е. .

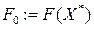Процесс продолжается до тех пор, пока список задач не будет исчерпан. В качестве оптимального решения исходной целочисленной задачи принимается решение задачи, которой соответствует максимальное .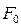

Пример 6.3. Решить следующую задачу целочисленного линейного программирования методом ветвей и границ:

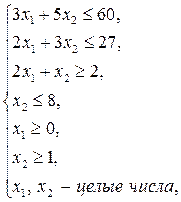
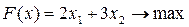
Решение: