2015-02-14
1491
Ферменный конечный элемент применяется для моделирования прямолинейных стержней конструкции, работающих на растяжение-сжатие (рис.1.2).
Рис. 1.2. Конечный элемент фермы: 1; 2 - локальные номера узлов; x- локальная ось, u1,u2- узловые перемещения в локальной системе координат.
В пределах каждого участка для случая для случая растяжения стержня формы перемещений задаются линейным полиномом:
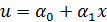(1.7)
Постоянные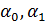 
определяются из условий:
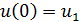
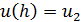
На основе выражения (1.7) получим два уравнения для нахождения 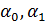через узловые перемещения:
,
;
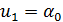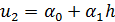Из которых определяем
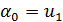
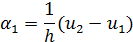
Тогда выражение (1.7) примет вид
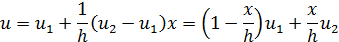
или в матричном представлении
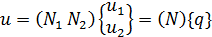(1.8)
где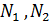 
функции Эрмита, отражающие форму перемещений в пределах конечного элемента:
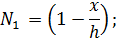
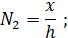
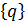- обобщенные координаты конечного элемента
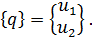
Равновесие элемента в обобщенных координатах имеет вид
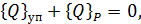
где
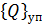- обобщенные силы от внутренних сил упругости элемента,
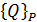- обобщенные силы от внешних активных сил.
Чтобы получить обобщенные силы от внутренних сил упругости и матрицу жесткости для ферменного элемента, запишем выражение потенциальной энергии внутренних сил элемента:
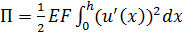; (1.9)
где
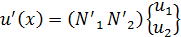(1.10)
причем
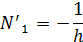
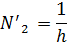
E- модуль упругости материала фермы, F - площадь поперечногосечения элемента.
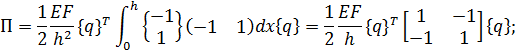
Обобщенные силы от внутренних сил упругости выражаются через потенциальную энергию
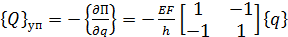(1.11)
Обозначим как матрицу жесткости элемента
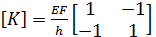. (1.12)
Обобщенные силы от внутренних сил упругости примут вид
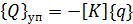(1.13)
где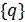 
– вектор-столбец обобщенных перемещений.
Обобщенные силы от внешних активных воздействий на элемент определим через возможную работу на обобщенных перемещениях
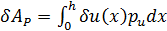(1.14)
где в соответствии с (8) вариация продольного перемещения
,
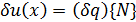а проекция распределенной нагрузки на продольное направление оси элемента при линейном законе распределения выражается через ее узловые значения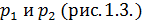 
:
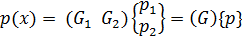, (1.15)
Рис. 1.3. Продольные распределенные внешние силы в элементе
При линейном законе распределения нагрузки
,
.
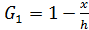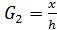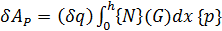(1.16)
где интеграл равен
,
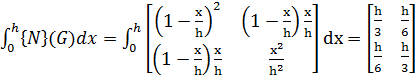Тогда
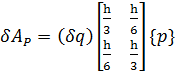. (1.17)
Коэффициенты в выражении возможной работы при соответствующих вариациях обобщенных координат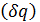 
называются обобщенными силами, то есть
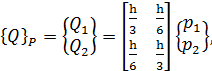(1.18)
где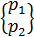 
- значения распределенной нагрузки в узловых точках.
В выражение (1.18) необходимо добавить сосредоточенные узловые активные силы, в проекции на направление обобщенных перемещений. Именно узловые силы как правило задаются для задачи о равновесии фермы.
Вернемся к условию равновесия в обобщенных координатах, представив его в виде
,
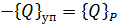Тогда для конечного элемента оно выглядит так:
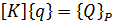(1.19)
При решении динамической задачи уравнения составляем на основе уравнений Лагранжа второго рода:
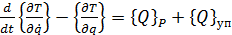(1.20)
где T – кинетическая энергия механической системы, которую необходимо выразить через обобщенные координаты:
,
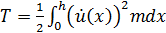где m – масса единицы длины стержневого элемента.
Выразим скорости точек элемента через обобщенные координаты и функции Эрмита, получим:
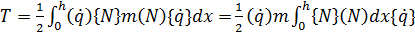(1.21)
Под интегралом в выражении (1.21) стоит квадратная матрица:
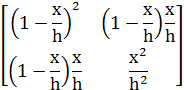
После вычисления интеграла получаем выражение кинетической энергии через произведение обобщенных скоростей и матрицы масс [ M ] размером 2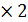 
.
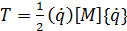, (1.22)
где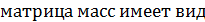 
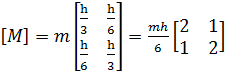(1.23)
Вычисляя производные в левой части уравнений Лагранжа второго рода (1.20), получим:
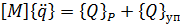
и с учетом соотношения (1.13) запишем
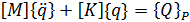(1.24)
Уравнение (1.24) определяет модель движения упругой динамической системы под действием внешних переменных сил.
