Формирование матриц жесткости и масс в глобальной системе координат для фермы

Узловые перемещения ферменного конечного элемента в локальной системе координат 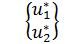выражаются через глобальные узловые обобщенные перемещения 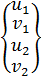и углы α и β рис.2.1 в виде

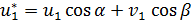
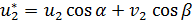
Рис. 2.1. Преобразование на плоскости узловых перемещений ферменного конечного элемента

В матричной форме это преобразование запишем так

где

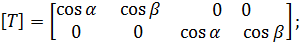(2.2)

;

Направляющие косинусы локальной оси 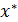определяются глобальными координатами узлов

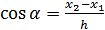, (2.3)

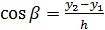, (2.4)

где

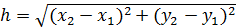(2.5)

длина элемента.

Матрица жесткости конечного элемента в глобальной системе координат преобразуется с учетом выражения (2.1) и зависимости для потенциальной энергии элемента, которая не зависит от выбора системы отсчета:

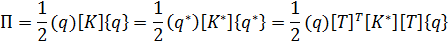
тогда

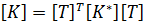(2.6)

Аналогично преобразуется и матрица масс конечного элемента 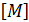, на основании того, что кинетическая энергия элемента не зависит от направления осей координат, по аналогии с потенциальной энергией получим:

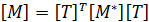(2.7)

Узловые силы приложены к узлам фермы и задаются в глобальной системе координат, поэтому в преобразованиях не нуждаются.

Рассмотрим, как формируется матрица жесткости и уравнения равновесия для механической системы, содержащей ферменные конечные элементы (рис. 2.2), к которой приложена сила P=300 кН. Известны размеры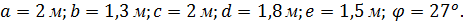

Без учета закрепления узлов необходимо ввести 12 обобщенных перемещений (по два на каждый из шести узлов). Матрица жесткости для такой системы будет иметь размер 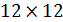, а матрица каждого элемента, приведенная к глобальной системе координат, имеет размер 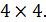Таким образом, конечные элементы, узлы которых совпадают должны вносить общий суммарный вклад в соответствующие элементы матрицы жесткости.

Рис. 2.2 Ферма с номерами узлов: 1...6 и номерами стержней 1...8 (в окружностях)

Рис. 2.3 Нумерация глобальных обобщенных координат для трех первых элементов с указанием в скобках номеров внутри элемента

Если условно обозначить матрицу жесткости первого элемента:

;

второго элемента:

;

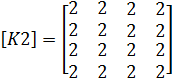третьего элемента:

;

то левый верхний угол общей матрицы жесткости без учета вклада других элементов примет вид

[K]=

2+1	2+1
2+1	2+1
		2+3	2+3
		2+3	2+3			...
				3+1	3+1
				3+1	3+1
		...

В качестве исходных данных для формирования матрицы жесткости потребуется координатная матрица для узлов и топологическая матрица для конечных элементов. Координатная матрица – это таблица, которая содержит информацию о номере узла и его координатах, а также о способе его закрепления и приложенных сосредоточенных силах. В соответствии с количеством узлов выбирается число обобщенных перемещений. Для конструкции рисунка 2.2 с учетом размеров 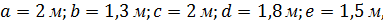координатная матрица имеет вид таблицы 2.1.