| № элемента | Номера перемещений начальный узел конечный узел | |||
По топологической и координатной матрицам вычисляются также направляющие косинусы и длины элементов (формулы (2.3),(2.4),(2.5)) и матрицы жесткости (1.12) и масс (1.23) для каждого элемента в отдельности. В строках матрицы индексов 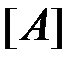 указаны глобальные номера узловых перемещений конечных элементов в порядке следования соответствующих им локальных номеров. Число строк в матрице
указаны глобальные номера узловых перемещений конечных элементов в порядке следования соответствующих им локальных номеров. Число строк в матрице 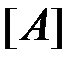 равно числу конечных элементов f1.m:
равно числу конечных элементов f1.m:
for (int i = 0; i < f1.m; i++)
{
// Формирование матрицы индексов
A[i, 0] = i + 1;
A[i, 1] = Convert.ToInt32(f1.MatrTop[i, 1]) * 2 - 1;
A[i, 2] = Convert.ToInt32(f1.MatrTop[i, 1]) * 2;
A[i, 3] = Convert.ToInt32(f1.MatrTop[i, 2]) * 2 - 1;
A[i, 4] = Convert.ToInt32(f1.MatrTop[i, 2]) * 2;
}
Затем с помощью матрицы индексов суммируем элементы отдельных матриц элементов в общую матрицу жесткости системы. Ниже приведен фрагмент программы на языке С# реализующий процесс сборки:
for (int ii = 0; ii < f1.m; ii++)
{
...//Формирование матрц элемента
for (int i = 1; i <= 4; i++)
{
int ig = A[ii, i];
for (int j = 1; j <= 4; j++)
{
int jg = A[ii, j];
K[ig - 1, jg - 1] = K[ig - 1, jg - 1] + Ke1[i - 1, j - 1];
M[ig - 1, jg - 1] = M[ig - 1, jg - 1] + Me1[i - 1, j - 1];
}
}
}
Обозначения в программе:
· ii – номер текущего конечного элемента;
· f1.m – число конечных элементов;
· A – матрица индексов перемещений;
· i, j – локальные индексы узловых перемещений конечного элемента;
· ig, jg – соответствующие им глобальные индексы, выбираемые из матрицы A;
· K –матрица жесткости конструкции;
· Ke1 – матрица жесткости текущего конечного элемента с номером ii, вычисленная в глобальной системе координат.
В этом же цикле формируется матрица масс M конструкции при решении динамической задачи.
 2015-02-14
2015-02-14 2489
2489
