Основные положения метода конечных элементов в механике упругого тела на примере плоской фермы

Метод конечных элементов основан на мысленном представлении сплошного тела в виде совокупности отдельных элементов, взаимодействующих между собой в конечном числе узловых точек (Рис.1.1). В этих точках прикладываются некоторые фиктивные усилия взаимодействия, характеризующие действие распределенных внутренних напряжений вдоль реальных границ стыков смежных элементов. Проблема определения напряженно-деформированного состояния сводится к расчету упругой системы с конечным числом степеней свободы.

Рис. 1.1 Стержневая механическая система.

Замена исходной физической системы совокупностью дискретных элементов подразумевает равенство энергий физической системы и ее дискретной модели. Характер взаимодействия между элементами должен быть таким, чтобы уменьшение размеров конечных элементов привело к получению решения, стремящегося к точному, если погрешность вычислений, связанная с увеличением размерности системы разрешающих уравнений, остается малой.

В пределах каждого конечного элемента перемещения аппроксимируются некоторыми функциями, которые должны удовлетворять следующим условиям:

- на границах между конечными элементами должны выполняться условия совместимости перемещений;

- в узлах конечных элементов эти функции должны давать перемещения, равные узловым перемещениям.

При решении статической задачи полная потенциальная энергия П системы, находящейся в равновесии, имеет минимум. Использование вариационного уравнения Лагранжа

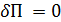(1.1)

дает уравнения равновесия для внешних и внутренних сил. Потенциальная энергия может быть представлена как функция узловых перемещений, поэтому уравнения равновесия, полученные по уравнению (1.1), связывают приведенные к узловым перемещениям внешние и внутренние силы

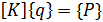, (1.2)

где 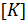- матрица жесткости механической системы; 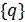- узловые перемещения (обобщенные координаты); {P}- вектор-столбец внешних узловых сил.

При решении динамической задачи, кроме потенциальной энергии П необходимо учесть кинетическую энергию системы T.

На основании общего уравнения динамики

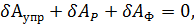
где 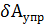- возможная работа упругих сил; 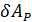- возможная работа внешних сил системы; 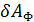- возможная работа сил инерции.

Если выбрать в качестве обобщенных координат узловые перемещения, то для голономной системы в соответствии с уравнениями Лагранжа второго рода можно записать

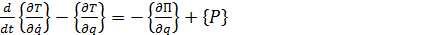(1.3)

где 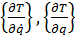- вектор-столбцы соответственно частных производных от кинетической энергии по обобщенным скоростям и координатам; 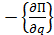- обобщенные потенциальные силы; 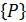- вектор столбец обобщенных активных сил. Для линейно-упругих систем уравнение (1.3) преобразуется к виду:

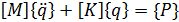, (1.4)

где 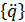- вектор столбец обобщенных ускорений; 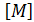- матрица масс системы, приведенных к узловым перемещениям. Матрицы масс и жесткостей определяются из выражений кинетической и потенциальной энергий системы соответственно

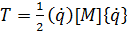; (1.5)

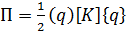. (1.6)

В случае малой упругой деформации элементы этих матриц считаются постоянными коэффициентами. Общая матрица 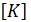составляется с помощью матриц жесткости каждого из элементов.