Исследование и оптимизация управляемой СМО

Очень важной, но до сих пор мало разработанной областью [18], является статистика систем массового обслуживания. Общая задача состоит в том, чтобы по наблюдениям за входящим и выходящим потоками требований управлять системой массового обслуживания. Оставаясь в рамках модели ВМ (глава 3), рассмотрим, каким образом происходит управление СМО. Так как ВМ СМО имеет конечное число приборов, то в системе возможна потеря заявок. Заявки, требующие для своего обслуживания больше приборов, чем имеется в системе свободных, теряются.

Вероятность потери заявки можно существенно уменьшить [8], если СМО допускает управляющие воздействия, состоящие в том, что в момент поступления заявки, требующей для своего обслуживания m приборов, ей может быть отказано даже при наличии i ³ m свободных приборов. Решение данной задачи предложено в работе [27], суть его состоит в следующем.

Математическая модель СМО. В качестве основы для построения математической модели управляемой системы СМО рассмотрим N -ли-нейную модель.

На вход системы поступает простейший поток с параметром l. Каждая заявка для своего обслуживания с вероятностью g (m) требует m приборов.

Пусть 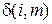– условная вероятность принять к обслуживанию поступившую заявку при условии, что она требует для своего обслуживания m приборов, а в системе имеется i свободных приборов. Очевидно, 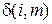= 0 при i < m, так как число требуемых приборов больше имеющегося числа свободных. Принятая заявка начинает обслуживаться одновременно на всех m выделенных для нее приборах. Заявка, получившая отказ в обслуживании, теряется и в дальнейшем не рассматривается.

Качество функционирования системы может оцениваться различными показателями, например вероятностью потери заявки, т.е. необходимо выбрать такие значения управляющих параметров 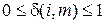, которые минимизируют вероятность потери заявки:

,

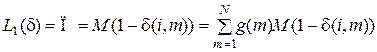где П – вероятность потери заявки с математическим ожиданием стационарного распределения P (i) состояний процесса i (t); i (t) – число свободных в момент t приборов.

Если заявки не равнозначны в смысле их потери, то показатель эффективности можно задать в виде:

,

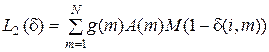где А (m)–коэффициент, определяющий значимость номера заявки, требующей для своего обслуживания m приборов.

Если необходимо минимизировать время простоя приборов, то показатель эффективности можно задать в виде

.

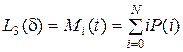Таким образом, показатель эффективности функционирования системы в общем виде можно определить как

,

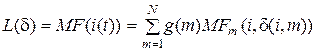где 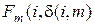) – величина издержек системы за единицу времени пребывания в i -м состоянии и принятие к обслуживанию в этом состоянии заявки, требующей m приборов.

Для исследования математической модели СМО рассмотрим случайный процесс i (t), состояниями которого является число приборов СМО, свободных в момент t. Этот процесс является марковским для любого заданного марковского уравнения .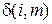

В стационарном режиме вероятности P (i) = P (i (t) = i)удовлетворяют системе уравнений:

;

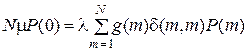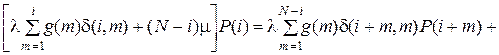(5.15)

,

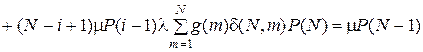решение которой для заданного управления 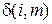не представляет труда. P (N) = S (N) – некоторое заданное число, например S (N) = 1, тогда из последнего уравнения системы (5.15) найдем значение S (N – 1) для P (N – 1). Далее из второго уравнения системы (5.15) при i = N – 1 определим S (N – 2) для P (N – 2), а при i = N – 2 найдем значение S (N – 3) и так далее до i = 1. При i = 1 определим значение S (0) для P (0). Найденные значения S (0), S (1), …, S (N) не противоречат первому уравнению системы (5.15), следовательно, являются решением этой системы.

Стационарное распределение вероятностей P (i) марковского процесса i (t) определяется следующим равенством:

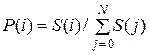, (5.16)

так как для P (i) выполняется условие нормировки 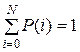и вектор Р (0), Р (1), …, Р (N) удовлетворяет системе (5.15).

Зная распределение (5.16), легко найти значения показателя эффективности функционирования системы при заданном управлении .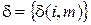

Например, пусть

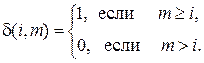(5.17)

Если N = 10, g (1) = 0,9; g (4) = 0,1 и 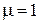, то .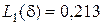

Заданное здесь уравнение (5.17) требует, чтобы принималась всякая заявка, для которой достаточно свободных приборов.

Функционирование управляемой СМО можно заметно улучшить, если выбрать оптимальные значения для управления 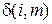. Как следует из работы [11], для нахождения оптимальных значений 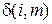достаточно решить систему нелинейных уравнений вида:

,

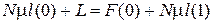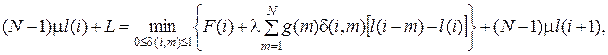
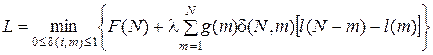, (5.18)

где .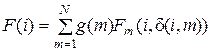

Методом последовательных преобразований в пространстве стратегий [28] решение системы (5.18) сводится к решению системы линейных алгебраических уравнений (СЛАУ).

Зададим произвольное управление d{d⁽¹⁾(i, m)}, например, в виде (5.17) и решим СЛАУ.

,

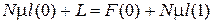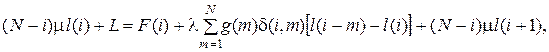(5.19)

,

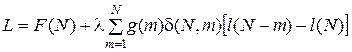где .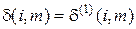

Зная решение 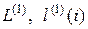этой системы, построим второе приближение в пространстве стратегий 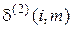, значения которых минимизируют выражения

.

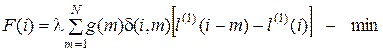Так как

,

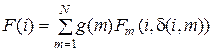то минимизация (5.19) – функции N переменных 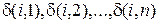– сводится к минимизации N функций вида

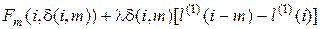(5.20)

одной переменной .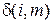

Там как во всех трех приведенных показателях эффективности – L ₁(d), L ₂(d), L ₃(d) – величины d(i, m) входят в функцию 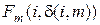линейно, то минимум выражения (5.20) достигается на границе интервала изменения 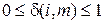, т.е. второе приближение 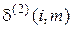принимает либо 0, либо 1.

Например, для критерия 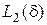второе приближение имеет вид

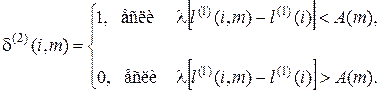
Подставляя 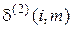в систему (5.18) и решая ее, определим 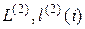. Зная 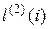, найдем следующее приближение в пространстве стратегий.

В работе [11] показано, что последовательность 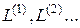монотонно убывает. Таким образом, алгоритм последовательных приближений в пространстве стратегий сходится. Как показывают результаты численных расчетов, достаточно 3–5 итераций для получения оптимального управления 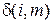и нахождения минимального значения .

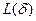В системе (5.19) число неизвестных l (0),…, l (N), L на единицу больше числа управлений, но l (i) определяется лишь с точностью до произвольного слагаемого, поэтому одну из неизвестных l (i) можно выбирать произвольно, тогда число уравнений становится достаточным для нахождения всех неизвестных. Но при численной реализации величину L удобнее находить, используя решение системы (5.15).

В самом деле, определив для заданного уравнения 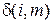величину L и положив 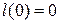, из первого уравнения (5.19) найдем l (1). Из второго уравнения системы (5.19), положив i = 1, определим l (2),а при i = 2 найдем l (3) и так далее. При i = N – 1 найдем значение l (N). Полученное значение L, l (0),…, l (N) не противоречит последнему уравнению системы (5.15), поэтому является ее решением.

Так как решение системы (5.15) и (5.19) сведено к рекуррентным процедурам пересчета, то их размерность не может служить существенным ограничением для применения предлагаемого подхода к решению поставленной задачи.

При тех же параметрах, что и ранее (N = 10, g (1) = 0,9, g (4) = 0,1 и 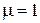), оптимальное значение 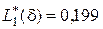, а выигрыш составляет 7 % по сравнению с неуправляемой системой.

Применяя указанную процедуру, можно уменьшить вероятность отказа заявки, несущественно усложняя процедуру функционирования СМО. Поэтому, с точки зрения системных характеристик, системы с управлением являются более эффективными (и экономически, и качественно), чем системы без управления.