2015-02-14
1379
Рассмотрим один из возможных оригинальных вариантов приоритетной модели СМО.
Предположим, что в СМО поступают два пуассоновских потока заявок с интенсивностями l1 и l2, причем l = l1 + l2. Заявки первого потока, являющиеся приоритетными, будем в дальнейшем называть 1-заявками, второго потока – 2-заявками. Кроме того, заявки требуют для своего обслуживания с вероятностью g (m) m обслуживающих приборов одновременно, g(0) = 0. Все обслуживающие приборы однородны в том смысле, что обслуживание на любом из них экспоненциальное с параметром m, а их число равно N. Освобождение приборов, занятых одной заявкой, происходит независимо друг от друга. Приоритет 1-заявок заключается в преимущественном праве на выделение требуемого числа обслуживающих приборов, которое осуществляется по следующему правилу: в случае, если пришедшая 2-заявка требует выделения такого числа приборов, которое в сумме с уже задействованными превышает некоторое заранее выбранное число n (n £ N), то она получает отказ в обслуживании. 1-заявке может быть отказано в обслуживании лишь в том случае, когда в наличии нет необходимого числа свободных приборов. Рассмотрим нахождение вероятностей отказа в обслуживании заявок обоих типов, которые обозначим соответственно П1 и П2.
|
|
|
Основное упрощение, облегчающее анализ, состоит в предположении наличия неограниченного числа приборов.
Рассмотрим случайный процесс, состоянием которого является число занятых приборов. Процесс является марковским, поэтому для него возможно построение стохастического графа переходов. Пусть Р (i) – вероятность того, что занято i приборов. Для нахождения Р (i), i = 0, 1, 2,…, n +1, с помощью стандартного метода сечений [9] получим систему (n + 1) уравнения с (n + 2) неизвестными:
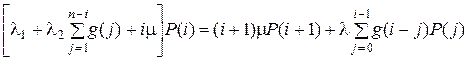, i = 0,1.
В качестве недостающего уравнения системы будем использовать условие нормировки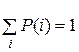 
, для нахождения которого необходимо рассмотреть вторую часть стохастического графа. Система уравнений, аналогичная вышеприведенной, запишется в следующем виде:
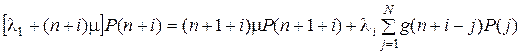, (5.4)
.
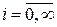Введем производящие функции:
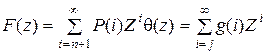. (5.5)
После суммирования уравнений (5.4) по i с использованием (5.5) получим
,
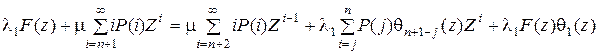откуда после некоторых преобразований имеем
,
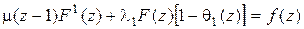где
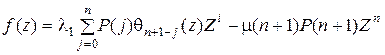
или в более компактном виде
.
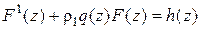Здесь
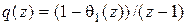, (5.6)
; 
.
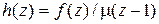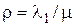Известно, что общее решение (5.6) может быть записано в виде
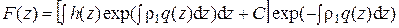, (5.7)
где С – произвольная постоянная.
Покажем, что Z = 1 является корнем f (z) и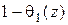 
, и найдем общий вид q (z) и h (z), удобный для использования в качестве подынтегрального выражения.
В силу определения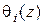 
выполняется 
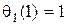. Далее имеем
;
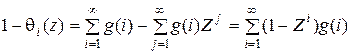следовательно,
.
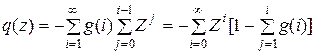Справедливость соотношения f (1) = 0 подтверждается тем, что оно в точности совпадает с уравнением сечения, проведенным между состояниями n и n + 1 стохастического графа. Теперь вычтем f (1) и f (z) и получим
|
|
|
.
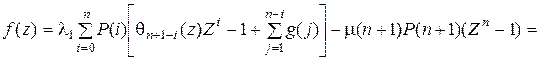
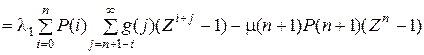Становится очевидным, что f (z) имеет единственный корень и выражение для h (z) приобретает следующий вид:
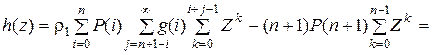
(5.8)
.
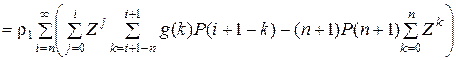Нетрудно заметить, что коэффициент при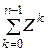 
представляет уравнение сечения между состояниями n и n + 1, поэтому, полагая его равным нулю, окончательно имеем
,
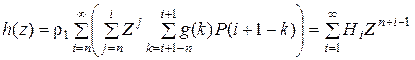где
.
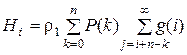Возвратимся теперь к анализу выражения (5.7). Обозначая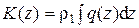 
и учитывая, что
,
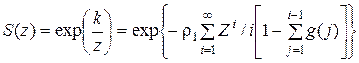осуществим разложение экспоненты в ряд по Z, взяв интеграл от произведения рядов h (z) и S (z). Так как
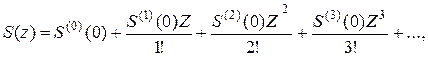
где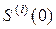 
– производная i -го порядка S (z) по Z в точке «0», то проблема заключается лишь в нахождении удобного соотношения для вычисления 
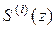, которое удается получить в виде
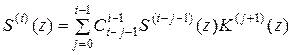, (5.9)
где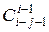 
– число сочетаний из i – 1 по i – j – 1; 
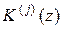– производная j -го порядка K (z) по Z, для которой имеет место
.
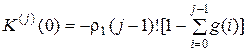Несколько первых значений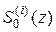 
, вычисляемых в соответствии с вышеприведенными формулами, имеют следующий вид:
,
,
,
.
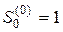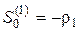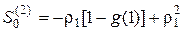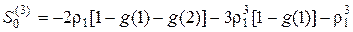С учетом (5.8) и (5.9) можно записать:
.
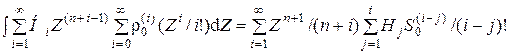Из условия F (0) = 0 определяем в выражении (5.7) С = 0. Таким образом, окончательно получаем
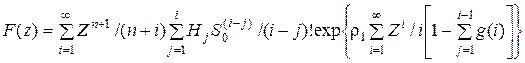. (5.10)
Это дает возможность добавить к исходной системе нормировочное условие
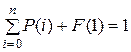
и найти все вероятности P (i), i = 0, …, n +1. Для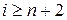 
вероятности P (i) легко определяются с помощью уравнений (5.4). Заметим, что выражение (5.10) для расчета F (1) представляет собой сумму бесконечного числа слагаемых, поэтому при реализации численного алгоритма рекомендуется использовать их конечное число, достаточное для того, чтобы решение системы не зависело от дальнейшего увеличения суммы ряда.
В качестве вероятностей блокировки потока i -го типа П i предлагается использовать следующие величины:
, 
,
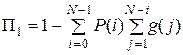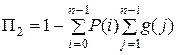которые, естественно, не совпадают точно с аналогичными характеристиками реальной системы, но являются вполне удовлетворительными их оценками. Проиллюстрируем изложенное на примерах.
Пример 5.1. Предположим, что число приборов, требуемое заявкой для обслуживания, распределено по геометрическому закону с параметрами q, т.е.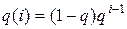 
, i = 1, …, 
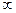. Тогда из соотношения (5.10) для F (1) получим:
.
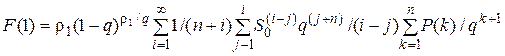В табл. 5.1 (столбец «Приближенно») приведены значения вероятностей блокировок, вычисленные с применением полученных соотношений, причем в выражении для F (1) использованы только первые четыре слагаемых в бесконечной сумме. В качестве критерия точности (столбец «Точно») предлагается взять результаты решения системы алгебраических уравнений, полученных стандартным методом сечения (что возможно лишь при небольших N). Варьирование входных параметров не оказывает существенного влияния на близость результатов.
Таблица 5.1
| Геометрическое распределение q = 0,5 | «Точно» | «Приближенно» | Равномерное распределение q = 0,2 | «Точно» | «Приближенно» |
| П1 | 0,010 | 0,012 | П1 | 0,034 | 0,038 |
| П2 | 0,191 | 0,196 | П2 | 0,446 | 0,453 |
Пример 5.2. Предположим теперь, что число требуемых приборов распределено равномерно на некотором интервале. Возьмем q (i) = 0,2, i = = 1, 2, …, 5. Из табл. 5.1 видно, что хорошее совпадение точных и приближенных результатов характерно и для этого типа распределения.
Отметим, что во всех случаях приближенное значение вероятности блокировки является пессимистической оценкой, что легко объяснимо на качественном уровне.
