2015-02-15
850
Теперь построим аппроксимирующую функцию дробно–рационального типа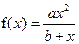 
. Для этого воспользуемся функцией genfit. Функция имеет следующие параметры:
· x, y – векторы, содержащие координаты заданных точек,
· F – функция, задающая искомую функциональную n –параметрическую зависимость и частные производные этой зависимости по параметрам.
· v – вектор, задающий начальные приближения для поиска параметров.
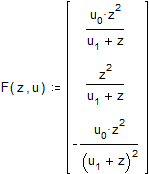
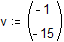
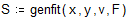
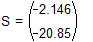
Поскольку нулевой элемент функции F содержит искомую функцию, определяем функцию следующим образом: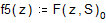 
Вычисляем среднее квадратичное отклонение
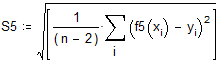
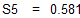
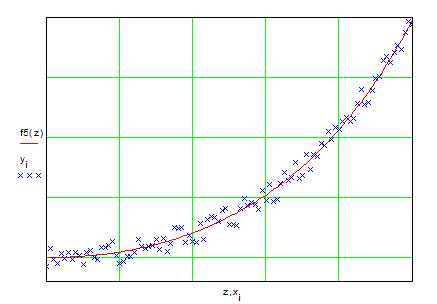
Функция genfit имеется не во всех реализациях Mathcad 'а. Возможно, однако, решить задачу, проведя линеаризацию.
Заданная функциональная зависимость может быть линеаризована введением переменных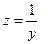 
и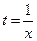 
. Тогда 
.
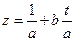Определим матрицы коэффициентов нормальной системы (см. книгу [8] из списка литературы)
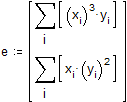
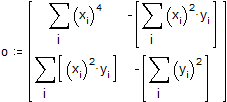
Находим коэффициенты функции, решая систему матричным методом,
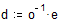
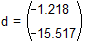
Определяем функцию: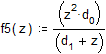 
Вычислим стандартное отклонение
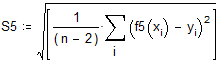
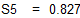
Обратите внимание! Мы получили другие коэффициенты! Вспомните, задача на нахождение минимума нелинейной функции, особенно нескольких переменных, может иметь несколько решений.
Стандартное отклонение больше, чем в случае аппроксимации полиномами, поэтому следует остановить свой выбор на аппроксимации полиномом.
Представим результаты аппроксимации на графиках
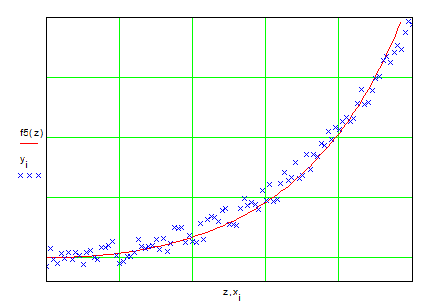
В тех случаях, когда функциональная зависимость оказывается достаточно сложной, может оказаться, что самый простой способ нахождения коэффициентов – минимизация функционала Ф "в лоб".
