 С.К.Клини
С.К.Клини
| Формализация понятия алгоритма в терминах рекурсивных функций предложена в 1936 году в работах А.Черча (общерекурсивные функции) и работах С.К.Клини (частично рекурсивные функции, 1938). |  А.Черч
А.Черч
|
Функция непосредственно следующее натуральное число, обозначаемая штрихом, позволяет по числу 0 построить любой начальный отрезок множества натуральных чисел. Обозначения при этом таковы: 0, 0/=1, 0//=1/,=2, …
Функции выбора аргумента определяются равенствами:
Wk(x1,x2, xk,…, xn)=xk (1£k£n).
Функция непосредственно следующее натуральное число, и функции выбора аргумента образуюттак называемое множество базисных функций. Функции, входящие в это множество всюду определены на множестве натуральных чисел.
Говорят, что функция может быть построена при применении оператора суперпозиции к функциямнескольких переменных, если она может быть определена в результате следующих действий:
1) подстановки функции в функцию;
2) переименовывания переменных;
3) отождествления переменных;
4) исключения переменных замещением их константами.
Пример 4.1.1. Даны функции g(y1,y2), w(x1, x2, x3). Говорят, что функция f(x1, y1, y2, x3)=w(x1, g(y1,y2), x3) построена путем подстановки функции g(y1,y2) в функцию w(x1, x2, x3).
Пример 4.1.2. Даны функции g(t), w(x1, x2, x3). Говорят, что функция f(x1,t,x3)=w(x1, g(t), x3) построена путем переименовывания переменных.
Пример 4.1.3. Даны функции g1(t), g2(t), w(x1, x2, x3). Говорят, что функция f(x1,t)=w(x1, g1(t), g2(t)) построена путем отождествления переменных.
Пример 4.1.4. Дана функция w(x1, x2, x3). Говорят, что функция f(x1,x3)= w(x1, m, x3) построена путем исключения переменных замещением их константами.
Оператор примитивной рекурсии применяется к двум функциям n-1 и n+1 переменных для построения функции n переменных.
Определяющие соотношения оператора примитивной рекурсии записываются так.
1. При n=1 по натуральному числу m и функции двух переменных h(u,v) строится функция одной переменной f(y):
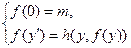 .
.
2. При n>1 по заданным функциям q(x1, x2, …, xn-1) и h(x1, x2, …, xn+1) строитсяфункция n переменных f(x1, x2,, xn–1, xn):
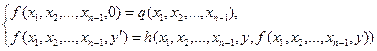 .
.
Определение 4.1.1. Функция называется примитивно рекурсивной, если она есть базисная функция или может быть построена исходя из базисных функций конечным числом применений операторов суперпозиции и примитивной рекурсии.
Пример 4.1.5. Функция g(x)=x – базисная. Функция h(x1, x2, x3)=x3 / может быть получена применением оператора суперпозиции двух базисных функций x3 / и w(x1, x2, x3)=x3. Исходяиз функций g(x)=x, h(x1, x2, x3) построим функцию двух переменных f(x,y) с применением оператора примитивной рекурсии:
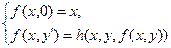
Таким образом, согласно определению эта функция является примитивно рекурсивной. В то же время, исходя из определения функции h(x1,x2,x3) запись функции f(x,y) можно сделать более наглядной:
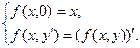
Или совсем простой – f(x,y)=x+y.
Последнее утверждение проверяется просто:
f(x,0)=x+0=x, f(x,y+1)=x+(y+1)=(x+y)+1= f(x,y)+1=(f(x,y))/.
Фактически в примере 5 мы доказали примитивную рекурсивность функции f(x,y)=x+y.
Аналогично доказывается примитивная рекурсивность функций:
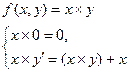 ,
, 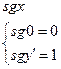
А также функций f(x,y)=xy, f(x)=x!.
Определение 4.1.2. Транзитивное замыкание множества базисных функций относительно операторов суперпозиции функций и примитивной рекурсии называется классом примитивно рекурсивных функций.
Определение 4.1.3. Говорят, что функция f(x1,x,2,…xn) получена из функций g(x1,x,2,…xn, z) и a(x1,x,2,…xn) с помощью ограниченного оператора минимизации (ограниченного m-оператора) и обозначают:
f(x1,x,2,…xn)= m z£a [ g(x1,x,2,…xn, z)= 0],
если f(x1,x,2,…xn)= z£a(x1,x,2,…xn)
тогда и только тогда, когда:
g(x1,x,2,…xn, k)¹0 при k =0, 1, 2, … z–1, и g(x1,x,2,…xn, z)= 0.
Теорема 4.1.3. Применение ограниченного m- оператора не выводит из класса примитивно рекурсивных функций.
 2015-02-18
2015-02-18 520
520








