Перечислимость и вычислимость

Определение 5.2.1. График функции y=f(x) – множество

F(x,y)={(x,y): y=f(x), x, y ÎN}

перечислим, если существует алгоритм, перечисляющий входящие в него пары, то есть существуют такие общерекурсивные функции s(s), t(s), что: F(x,y)={(x,y): x= s(s), y= t(s), s ÎN}.

Теорема 5.2.1. Функция y=f(x) с непустойобластьюопределения вычислима тогда и только тогда, когда ее график F(x,y)={(x,y): y=f(x), x, y ÎN} является перечислимым множеством.

Доказательство. Пусть график F(x,y) некоторой функции y=f(x) является перечислимым множеством. Тогда перечислимым множеством является P – область определения функции y=f(x): P={ x: x= s(s), s ÎN}.

Для вычисления f(n) в данной точке n ÎP необходимо.

1. Вычисляя последовательно s(0), s(1) …, найти первое по порядку число s ÎN такое, что s(s)= n. Так как n ÎP, то такое число s обязательно найдется и будет равно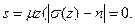

2. Вычислить значение m= t(s) и положить f(n)=m.

Таким образом, если график F(x,y) – перечислимое множество, то y=f(x) – вычислимая функция, которая определяется так:

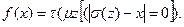
Заметим, что вычисление значения функции в точке, не принадлежащей области определения, приводит к бесконечным вычислениям последовательности s(0), s(1) ….

Предположим теперь, что функция y=f(x) – вычислима. В этом случае найдется машина Тьюринга T, такая что T(x)= f(x). Тогда в точках, принадлежащих области определения функции, она будет останавливаться и давать точки, принадлежащие графику F(x,y). В точках, не принадлежащих области определения функции, эта машина Тьюринга будет работать бесконечно. Так что график будет перечислимым множеством.

¨Теорема доказана.