2015-02-18
387
1 Признак сравнения.
Даны два знакоположительных ряда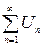 
и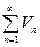 
. Пусть, начиная с некоторого n, может быть и с n= 1, выполняется 
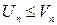, тогда:
а) если 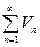сходится, то сходится и ;
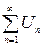б) если 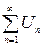расходится, то расходится и 
.
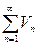Следствие: если существует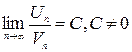 
, конечное число, то ряды сходятся или расходятся одновременно.
Для использования этого признака удобно выбирать ряд, составленный из членов геометрической прогрессии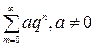 
, который сходится при 
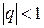и расходится при 
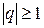, а также обобщенный гармонический ряд 
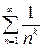, который сходится при 
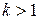и расходится при 
.
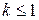2 Признак Даламбера.
Пусть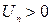 
и существует 
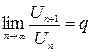. Тогда при q <1 ряд сходится, при q >1 – расходится, при q =1 – сомнительный случай (нужно исследовать с помощью других признаков).
3 Радикальный признак Коши.
Пусть 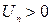и существует 
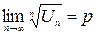. Тогда при p <1 ряд сходится, при p >1 – расходится, при p =1 – сомнительный случай.
4 Интегральный признак Коши.
Дан знакоположительный ряд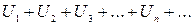 
| (1) |
Пусть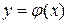 
– непрерывная, положительная, монотонно убывающая функция, определенная при 
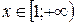и такова, что члены ряда являются значениями функции при 
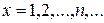, т. е. 
, 
, …, 
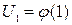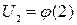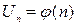,…, тогда ряд (1) и несобственный интеграл 
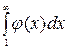сходятся или расходятся одновременно.
План исследования знакоположительных рядов
1. Находим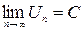 
. Если 
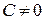, то ряд расходится, исследование закончено.
2. Если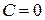 
, применяем один (подходящий) из достаточных признаков сходимости.
3. Делаем вывод о сходимости ряда.
Примеры.
1) 
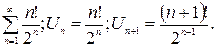
Напоминаем, что
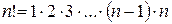; 0!=1;
.
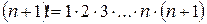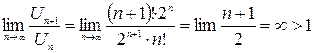– ряд, расходящийся по признаку Даламбера.
2) 
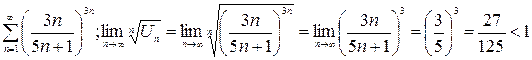– ряд сходится по радикальному признаку Коши.
3) 
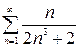сравним с 
– сходящимся (как обобщенный гармонический 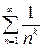при k >1). Используем следствие из признака сравнения: 
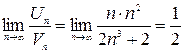– конечное, не равное нулю число, тогда ряды ведут себя одинаково, т. е. сходятся.
