Степенным рядом называется ряд вида:
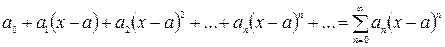 ,
,
где 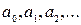 – постоянные величины, коэффициенты ряда, число a – центр ряда.
– постоянные величины, коэффициенты ряда, число a – центр ряда.
При a =0 имеем
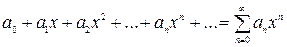
| (1) |
При 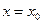 степенной ряд (1) принимает вид
степенной ряд (1) принимает вид
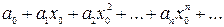
| (2) |
Это уже числовой ряд. он может сходиться или расходиться.
Если ряд (2) сходится, то 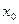 – точка сходимости степенного ряда (1). Если ряд (2) расходится, то
– точка сходимости степенного ряда (1). Если ряд (2) расходится, то 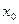 – точка расходимости. Совокупность точек сходимости называется областью сходимости степенного ряда.
– точка расходимости. Совокупность точек сходимости называется областью сходимости степенного ряда.
Теорема Абеля. Для любого степенного ряда (1) существует интервал 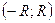 , внутри которого ряд сходится абсолютно, вне его расходится, а на границах может иметь различный характер сходимости.
, внутри которого ряд сходится абсолютно, вне его расходится, а на границах может иметь различный характер сходимости.
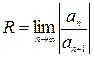 – радиус интервала сходимости.
– радиус интервала сходимости.
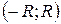 – интервал сходимости.
– интервал сходимости.
Если R =0, то точка x =0 – единственная точка сходимости.
Если R =¥, то ряд сходится на всей числовой оси.
Пример.
1) Найти радиус и интервал сходимости степенного ряда. Исследовать сходимость ряда на концах интервала.
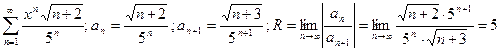 .
.
Тогда (-5; 5) – интервал, внутри которого ряд сходится абсолютно. Исследуем характер сходимости ряда на границах.
1) x =–5, тогда степенной ряд примет вид
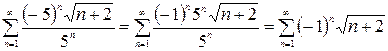 .
.
Это знакочередующийся ряд. Для него применим признак Лейбница:
1) 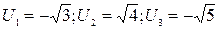
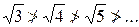 – не выполнено первое условие признака Лейбница, тогда ряд
– не выполнено первое условие признака Лейбница, тогда ряд
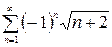 расходится, точка
расходится, точка 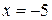 – точка расходимости.
– точка расходимости.
2) x =5; 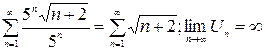 – ряд расходится по следствию из необходимого признака, тогда x =5 – точка расходимости.
– ряд расходится по следствию из необходимого признака, тогда x =5 – точка расходимости.
(-5; 5) – область сходимости данного степенного ряда.
2) 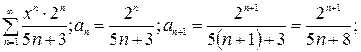
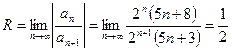 .
.
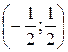 – интервал сходимости данного степенного ряда. Исследуем на границах:
– интервал сходимости данного степенного ряда. Исследуем на границах:
1) 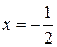 , тогда степенной ряд примет вид:
, тогда степенной ряд примет вид:
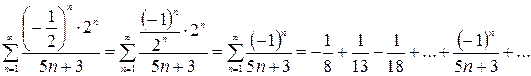 – это знакочередующийся ряд. Проверим два условия:
– это знакочередующийся ряд. Проверим два условия:
1) 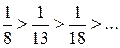 ;
;
2) 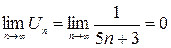 , тогда ряд
, тогда ряд 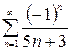 сходится по признаку Лейбница, точка
сходится по признаку Лейбница, точка 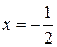 – есть точка сходимости первоначального степенного ряда, она входит в область сходимости.
– есть точка сходимости первоначального степенного ряда, она входит в область сходимости.
2) 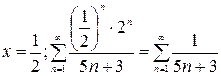 . Сравним этот ряд с гармоническим
. Сравним этот ряд с гармоническим 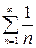 , который, как известно, расходится.
, который, как известно, расходится.
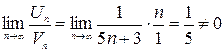 – конечное число, тогда по следствию из признака сравнения ряды ведут себя одинаково, т. е. оба расходятся, поэтому точка
– конечное число, тогда по следствию из признака сравнения ряды ведут себя одинаково, т. е. оба расходятся, поэтому точка 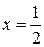 – точка расходимости начального степенного ряда.
– точка расходимости начального степенного ряда.
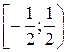 – область сходимости степенного ряда.
– область сходимости степенного ряда.
 2015-02-18
2015-02-18 431
431








