2015-02-18
585
Сложное высказывание будем назвать тождественно истинным или тавтологией, если оно принимает значение истины для всех наборов значений входящих в него простых высказываний.
Два сложных высказывания будем называть равносильными, если их значения совпадают при одних и тех же наборах значений входящих в них простых высказываний.
Доказательство приведенных ниже основных равносильностей алгебры высказываний выполняется при помощи составления таблиц истинности.
1. Закон тождества: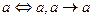 
;
2. Закон непротиворечия: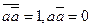 
;
3. Закон исключенного третьего: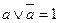 
;
4. Закон двойного отрицания: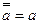 
;
5. Законы ассоциативности: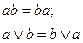 
;
6. Законы коммутативности: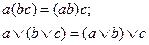 
;
7. Законы дистрибутивности: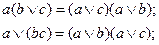 
8. Законы поглощения: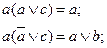 
9. Законы де Моргана: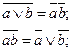 
10. Связь конъюнкции, дизъюнкции, импликации и отрицания: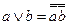 
;
11. 
:
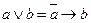12. 
;
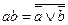13. 
;
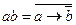14. 
;
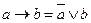15. 
;
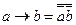16. Модусы (разновидности схемы утверждений):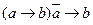 
-утверждающий модус;
17. 
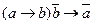- отрицающий модус;
18. Отрицающе-утверждающий модус: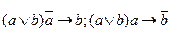 
;
19. Законы транзитивности: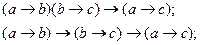 
20. Законы контрапозиции: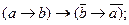 
21. 
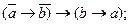
22. 
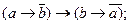
23. 
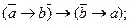
24. 
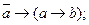
25. 
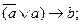
26. Законы косвенного доказательства: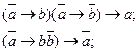 
27. Законы Клавия: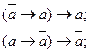 
В качестве примера докажем, что, например, формулы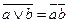 
и 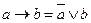являются тождественно истинными (тавтологиями), построив для их левых и правых частей таблицы истинности и используя табличные определения основных логических операций
1.
| 
| 
| 
| 
| 
| 
|
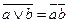
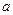
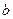
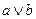
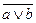
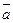
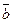
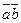
В четвертом и седьмом столбцах полученной таблицы содержаться истинностные значения, соответствующие левой и правой частям рассматриваемой формулы, и принимаемые этими выражениями значения одинаковы для всех наборов простых переменных, входящих в состав сложного высказывания. Значит, данная формула является тавтологией.
2.
|
|
| 
|
| 
|
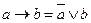
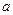
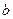
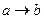
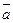
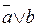
В третьем и пятом столбцах полученной таблицы содержатся истинностные значения, соответствующие левой и правой частям рассматриваемой формулы, и принимаемые этими выражениями значения одинаковы для всех наборов простых переменных, входящих в состав сложного высказывания. Значит, данная формула также является тавтологией.
Пример:
