Задача: В замке есть две комнаты, в каждой из которых может находиться либо тигр, либо принцесса. На дверях комнат имеются таблички следующего содержания: табличка I - «По крайней мере в одной из комнат находится принцесса», табличка II – «Принцесса находится в другой комнате».
Если в первой комнате находится принцесса, то утверждение на табличке I истинно, если тигр – то ложно. Для второй комнаты наоборот, если там находится принцесса, то утверждение на табличке II ложно, а если там находится тигр – то это утверждение истинно. Определить, в какой из комнат находится принцесса.
Решение:
Введем обозначения для простых высказываний, необходимые для формализации условия задачи, обозначив соответственно через П1 высказывание «принцесса находится в первой комнате», через П2 - высказывание «принцесса находиться во второй комнате», тогда высказывание «тигр находится в первой комнате» есть отрицание переменной П1, а высказывание «тигр находится во второй комнате» - отрицание высказывания П2.
Тогда надпись на первой двери (обозначим это сложное суждение через А) можно представить в виде конъюнкции высказываний П1 и П2 (А=П1 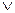 П2), а надпись на второй двери (обозначим его через В) совпадает с высказыванием П1, т.е. В=П1.
П2), а надпись на второй двери (обозначим его через В) совпадает с высказыванием П1, т.е. В=П1.
Учитывая условие, что при нахождении в первой комнате принцессы утверждение на табличке I истинно, тигра – то ложно, а для второй комнаты при нахождении в ней принцессы утверждение на табличке II ложно, нахождения в ней тигра это утверждение истинно, получим в формализованном виде следующую запись условия нашей задачи:
(П1*А 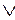 П1*А)*(П2*В
П1*А)*(П2*В 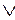 П2*В)=
П2*В)=
=(П1*(П1 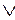 П2)
П2) 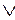 П1* (П1
П1* (П1 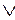 П2))(П2*П1
П2))(П2*П1 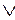 П2*П1)=
П2*П1)=
= П1* П2.
1. П1*(П1 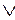 П2)
П2) 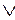 П1* (П1
П1* (П1 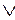 П2)= П1*П2
П2)= П1*П2 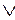 П1
П1 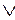 П1* П1*П2=
П1* П1*П2=
= П1*П2 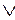 П1
П1 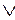 П1*П2=П1
П1*П2=П1 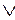 П2;
П2;
2. (П2*П1 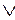 П2*П1)* (П1
П2*П1)* (П1 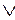 П2) =
П2) =
= П2*П1*П1 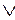 П2*П1*П2
П2*П1*П2 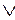 П2*П1*П1
П2*П1*П1 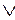 П2*П1*П2=
П2*П1*П2=
= П1* П2.
Замечание: жирным шрифтом здесь отмечены нулевые конъюнкции, 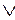 - знак операции дизъюнкция, * - знак операции конъюнкция, - знак операции отрицания.
- знак операции дизъюнкция, * - знак операции конъюнкция, - знак операции отрицания.
С учетом введенных обозначений для переменных П1 и П2 (П1- «принцесса находится в первой комнате», П2 – «принцесса находится во второй комнате») и полученной в результате преобразований формуле П1* П2 можем сформулировать ответ на вопрос задачи – принцесса находится в первой комнате.
Примеры:
а) Проверьте равносильность двумя способами:
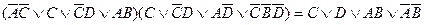
Первый способ проверки равносильностей - при помощи построения таблиц истинности ля левой и правой части формулы. Если истинностные значения в соответствующих столбцах совпадают при любых наборах значений составляющих простых суждений, то равносильность считается доказанной, в противном случае она не имеет места.
Составим таблицы истинности для левой и правой частей приведенной формулы (табл. 2, табл.3):
Таблица 2
| А | B | C | D | А B | 5+3 | 3D | AB | 6+7 | 9+6+8 | 6+11+12 | 13*10 | ||||||
|
| А | B | C | D | А B | AB | 3+4+5+6 |
Второй способ проверки равносильностей алгебры логики- преобразование исходной формулы на основании известных. Ранее доказанных основных равносильностей алгебры высказываний.
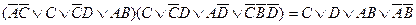
Используем для доказательства метод приведения левой части фрмулы к правой:
1) 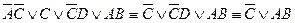 ;
;
2) 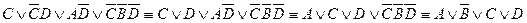 ;
;
3) 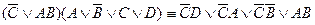 ;
;
4) 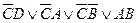 ≠
≠ 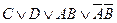 .
.
Так как левая часть в результате равносильных преобразований не эквивалентна правой, можно сделать вывод, о том, что данная формула не является равносильностью алгебры высказываний.
в) Найдите отрицание приведенного сложного высказывания:
Если урок будет интересным, никто из мальчиков — Петя, Ваня, Коля — не будет смотреть в окно;
Ведем обозначения для простых суждений, входящих в состав приведенного сложного суждения и воспользуемся общим правилом отрицания сложных суждений. Пусть П - суждение «Петя посмотрит в окно», В - суждение «Ваня посмотрит в окно», К - суждение «Коля посмотрит в окно», И – «урок будет интересным». Тогда, формализуя исходное сложное суждение и учитывая, что нужно найти его отрицание, получим:
(И→ ПВК)↔ И*(П+В+Л)
Следовательно, отрицание исходного сложного суждения можно сформулировать в виде: «Урок будет интересным, но хотя бы один их мальчиков (Петя, Ваня, Коля) будет смотреть в окно».
 2015-02-18
2015-02-18 794
794








