Перевод некоторых (наиболее часто встречающихся) выражений естественного языка на символический язык алгебры логики
| Форма высказывания естественного языка | Соответствующая формула языка алгебры логики |
| Не А; неверно, что А; А не имеет места | 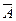
|
| A и В; как А, так и В; не только А, но и В; А вместе с В; А, несмотря на В; А, в то время как В | 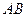
|
| А, но не В; не В, а А | 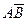
|
| А или В; А, или В, или оба | 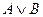
|
| А либо В; А, разве что В; либо А, либо В; не А, разве что не В; либо не А, либо не В; А или В, но не оба | 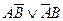
|
| Либо А, либо В и С; А, разве что В и С | 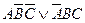
|
| Либо А и В, либо С и D | 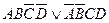
|
| Если А, то В; В, если А; А, только если В; А только тогда, когда В; А достаточно для В; А только при условии, что В; В необходимо для А; А. значит В; для В достаточно А; А влечет В; для А необходимо В; все А есть В; из А следует В; В тогда, когда А | 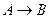
|
| А эквивалентно В; А тогда и только тогда, когда В; А если и только если В; А необходимо и достаточно для В | 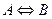
|
 2015-02-18
2015-02-18 460
460








