Выполним суммирование слева направо в порядке записи (как ЭВМ):
+ 0,476 + 0,887 + 2,36 + 28,6
0,411 1,47 26,2 83,




0,887»0,887 2,357»2,36 28,56»28,6 111,6» 112.
Пусть теперь выражение записано в обратном порядке:
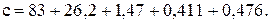
Выполним суммирование как ЭВМ:
+ 83 + 109 +110 + 110
26,2 1,47 0,411 0,476
 |  |  |  |
109,2»109 110,47»110 110,411»110 110,476» 110
От перестановки слагаемых сумма изменилась, то есть
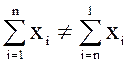
Пример 2.2
Требуется перемножить 100 чисел, причем первая половина из них равна 0,1, вторая 10 (числа упорядочены по возрастанию значений).
Если в программе на языке Pascal последовательно перемножать числа, начиная с первого, то результат будет равен 0 (самое маленькое по модулю значение переменной типа Real на языке Pascal ± 2,9 ·10-39 ).
Если же последовательно перемножать с конца, то произойдет переполнение (самое большее по модулю значение переменной типа Real на языке Pascal 1,7·10 38 ).
Если же эти значения чередуются, то независимо от порядка умножения результат будет равен 1,0.
Следовательно, от перестановки мест сомножителей значение произведения в рассмотренном случае меняется.
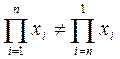
В машинной арифметике законы коммутативности ( переместительный ) и дистрибутивности ( распределительный ) не всегда соблюдаются.
Рекомендации для снижения ошибок округления:
1. При сложении и вычитании последовательности чисел действия необходимо начинать с наименьших по абсолютной величине значений.
2. Следует избегать вычитания двух близких чисел, преобразуя выражения.
3. Количество арифметических действий для решения задачи нужно сводить к минимуму.
4. Для уменьшения ошибки округления расчеты следует проводить с повышенной разрядностью (doubleprecisionв Pascal).
При выборе численного метода решения задачи необходимо учитывать следующее:
1. Погрешность метода должна быть на порядок меньше неустранимой погрешности. Увеличение погрешности метода снижает точность, уменьшение – увеличивает время решения задачи.
2. Погрешность округления должна быть значительно меньше (на два порядка) погрешности метода и неустранимой погрешности.
Для оценки погрешности решения на практике можно использовать следующие приемы:
1. Решить задачу различными численными методами и результаты сравнить.
2. Незначительно изменить исходные данные и повторно решить задачу. Результаты сравнить. Если они различаются сильно, задача или метод ее решения являются неустойчивым – выбрать другой.
Тема 3
Численное решение алгебраических и трансцендентных урав нений.
Решение уравнений – это одна из древнейших математических задач. Ещё в Древней Греции умели решать линейные и квадратные алгебраические уравнения. В эпоху Возрождения (XV век) Джироламо Кардано и его ученик Луиджи Феррари получили точные решения для алгебраических многочленов 3 и 4 степени. Позднее много усилий было затрачено на получение точного решения многочленов 5 степени и выше. Но только в 20-х годах XIX века было доказано, что решение алгебраического многочлена n-ой степени
an x n + an-1xn-1 +...+ a0 = 0, где an ¹ 0
при n ³ 5 нельзя выразить через коэффициенты с помощью арифметических действий и операций извлечения корня.
Известно, что алгебраический многочлен n-ой степени имеет n корней, причём они могут быть вещественными и комплексными (теорема Гаусса).
Решение трансцендентных уравнений в явном виде также может быть получено в редких, простейших случаях. Трансцендентные уравнения, включающие алгебраические, тригонометрические, экспоненциальные функции от неизвестного x, как правило, имеют неопределённое число корней. Необходимость решения трансцендентных уравнений возникает, например, при расчёте устойчивости систем, расчете парожидкостного равновесия и т.п.
Достаточно распространенной задачей является так же нахождение некоторых или всех решений системы из n нелинейных алгебраических или трансцендентных уравнений с n неизвестными.
Рассмотрим вначале методы решения нелинейных уравнений с одним неизвестным.
Пусть задана непрерывная функция f(x) и требуется найти корни уравнения
f(x)=0 (3.1)
на всей числовой оси или на некотором интервале 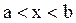 .
.
Всякое значение 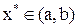 , удовлетворяющее условию
, удовлетворяющее условию 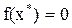 , называется корнем уравнения (6.1), а способ нахождения этого значения
, называется корнем уравнения (6.1), а способ нахождения этого значения 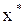 и есть решение уравнения (3.1).
и есть решение уравнения (3.1).
Методы решения уравнений:
· Прямые (формула Виета для квадратного уравнения и Кардано для кубического и другие)
· Итерационные – для решения любого уравнения
Численное решение уравнения проводится в два этапа:
1 этап. Отделение корней уравнения.
2 этап. Уточнение интересующих корней с заданной точностью ε.
3.1. Отделение корней нелинейного уравнения.
Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a,b], которому он принадлежит.
На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.
В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается аналитическими и графическими методами.
Аналитические методы основаны на функциональном анализе.
Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида
Pn(x) = an x n + an-1xn-1 +...+a1x+ a0 = 0, (an >0) (3.2)
верхняя граница положительных действительных корней 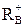 определяется по формуле Лагранжа (Маклорена):
определяется по формуле Лагранжа (Маклорена):
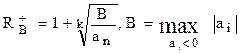 , (3.3)
, (3.3)
где: k ³ 1 – номер первого из отрицательных коэффициентов полинома;
B – максимальный по модулю отрицательный коэффициент.
Нижнюю границу положительных действительных корней 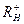 можно определить из вспомогательного уравнения
можно определить из вспомогательного уравнения
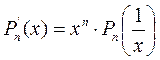 (3.4)
(3.4)
Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то
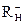 =
= 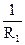 (3.5)
(3.5)
Тогда все положительные корни многочлена лежат в интервале
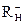 ≤x+≤
≤x+≤ 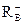 .
.
Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.
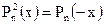 и
и 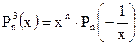 .
.
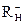 ≤x–≤
≤x–≤ 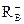
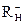 =
= 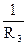
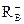 =
= 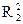 .
.
Рассмотрим пример отделения корней с использованием этого аналитического метода.
Методом Лагранжа определим границы положительных и отрицательных корней многочлена.
3x8 – 5x7 – 6x3 – x – 9 = 0
k = 1 B = |– 9| an = 3
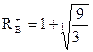 = 4
= 4
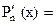 9x8 + x7 + 6x5 + 5x – 3 = 0
9x8 + x7 + 6x5 + 5x – 3 = 0
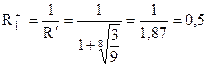 |
k = 8 B = 3 an = 9
Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4
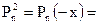 3x8 + 5x7 + 6x3 + x – 9 = 0
3x8 + 5x7 + 6x3 + x – 9 = 0
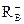 =
= 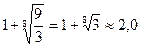
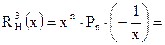 9x8 – x7 – 6x5 – 5x – 3 = 0
9x8 – x7 – 6x5 – 5x – 3 = 0
k = 1 B = 6 an = 9
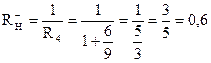 |
Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6
Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.
Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.
На практике получил большее распространение графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.
Графически корни можно отделить 2-мя способами:
1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.
|
|
|
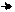

|


|
|
|
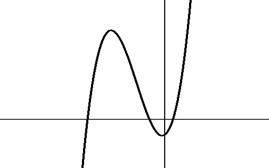
Рис. 3.1 Отделение корней на графике f(x).
|
2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.
| |||
 | |||

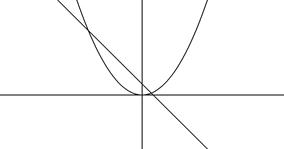
Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).
Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.
Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.
Рассмотрим схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.
Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.
Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.
Недостаток метода – использование большого количества машинного времени.
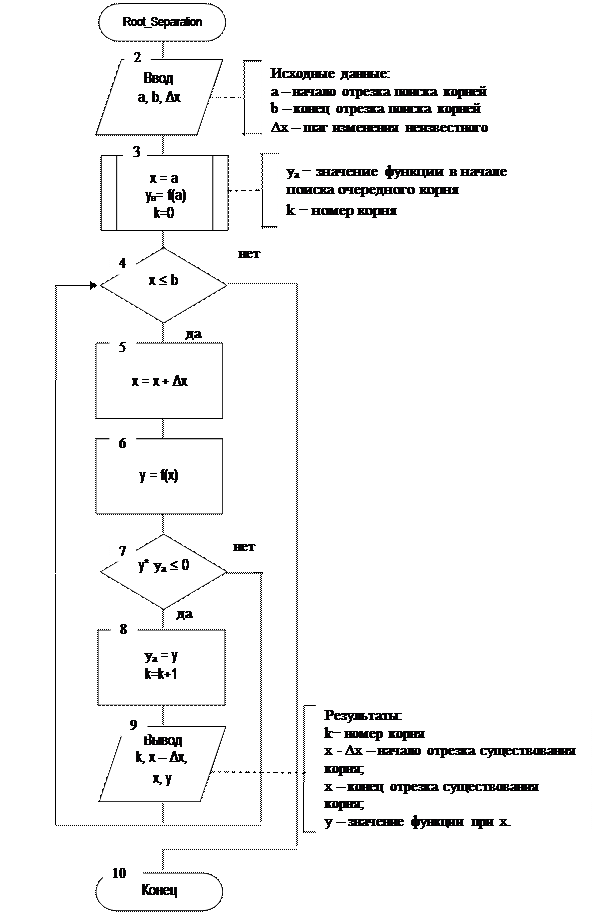 |
Рис. 3.3 Схема алгоритма отделения корней.
3.2. Алгоритмы уточнения корней уравнения.
Уточнение корня – это вычисление интересующего корня с заданной точностью e.
Приближённые значения корней уравнения, полученные на предыдущем этапе, уточняются различными итерационными методами.
Рассмотрим некоторые из них.
3.2.1. Метод дихотомии (половинного деления, бисекций).
Постановка задачи:
Дано нелинейное уравнение ¦(x) = 0.
Корень отделен, т.е. известно, что x* Î [a,b].
Требуется вычислить корень с заданной точностью ε.
Метод реализует стратегию постепенного уменьшения отрезка существования корня, используя факт изменения знака функции в окрестности корня.
Алгоритм метода.
1. Вычислить координату середины отрезка [a,b] x = (a+b)/2 и значение ¦(x) в этой точке.
2. Уменьшить отрезок, отбросив ту его половину, на которой корня нет.
Если знак функции в начале отрезка и в его середине одинаков, то корень находится на второй половине, первую половину можно отбросить, переместив начало отрезка в его середину:
если ¦(a) ·¦(x)>0 => x*Î [x,b] => a=x, иначе x*Î [a, x] => b=x
3. Проверить условие завершения вычислений: длина отрезка не превышает заданную точность и значение функции близко к 0 с заданной точностью:
b-a ≤ ε ∩ |¦(x)| ≤ ε.
Если условие достигнуто, расчет завершен, иначе повторить алгоритм сначала.
 |
|
|
|
|
|
|

Рис. 3.4 Геометрическая иллюстрация метода бисекций.
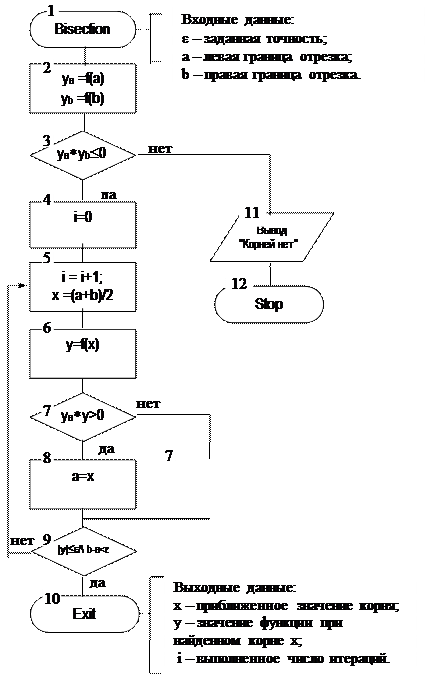
|
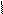
Рис. 3.5 Схема алгоритма метода бисекций (дихотомии)
Количество итераций n, требуемых для достижения требуемой точности ε можно оценить заранее из соотношения
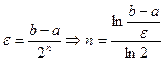 (3.6)
(3.6)
Метод дитохомии − простой и надежный метод поиска простого корня любой функции, устойчивый к погрешности округления. Даже если на отрезке есть несколько корней (нечетное количество),то будет найден один из них.
Недостатки метода: скорость сходимости низкая, не обобщается на систему уравнений.
 Метод дихотомии нельзя использовать для уточнения не простого корня − корень совпадает с точкой экстремума функции, т.к. в этом случае функция не изменяет свой знак в окрестности корня.
Метод дихотомии нельзя использовать для уточнения не простого корня − корень совпадает с точкой экстремума функции, т.к. в этом случае функция не изменяет свой знак в окрестности корня.
Рис. 3.6. Непростой корень уравнения.
Пример 3.1. Требуется решить уравнение x3+2x=1
Сначала нужно отделить решения.
 Удобно записать уравнение в виде x3=1-2x и построить графики двух элементарных функций ¦1(x)= x3 и ¦2(x)=1-2x
Удобно записать уравнение в виде x3=1-2x и построить графики двух элементарных функций ¦1(x)= x3 и ¦2(x)=1-2x
Рис. 3.7 Отделение корней уравнения x3 = 1 - 2 x.
Из графика следует, что корень один: x* Î [0;1].
Проверим наличие корня на отрезке
¦(a) = ¦(0) = 03+2·0 = -1, ¦(b) = ¦(1) = 13+2·1 = 2
Знаки на концах отрезка разные, следовательно, корень отделен верно.
Выполним несколько итераций уточнения корня.
1 итерация. Середина отрезка x = (0 + 1) / 2 = 0,5
Значение функции в середине ¦(x)=¦(0,5)= 0,53+2·0,5-1=0,125>0
Функция меняет свой знак на первой половине отрезка, следовательно, корень на первой половине, поэтому отбросим вторую половину, переместив конец отрезка в середину: x* Î [0;0,5]
2 итерация. Середина отрезка x = (0 + 0,5) / 2 = 0,25
Значение функции в середине
¦(x)=¦(0,25)= 0,253+2·0,25-1=0,0115625-0,5=-0,484375
Функция не меняет свой знак на первой половине отрезка, поэтому отбросим ее: x* Î [0,25;0,5]
Вычисления следует продолжить до достижения требуемой точности. Например, если ε=0,001 то потребуется не менее 10 итераций:
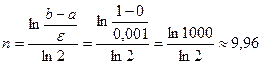
3.2.2. Метод простых итераций (метод последовательных приближений).
Метод реализует стратегию постепенного уточнения значения корня.
Постановка задачи. Дано нелинейное уравнение (3.1). Корень отделен x* Î [a;b]. Требуется уточнить корень с точностью ε.
Уравнение (3.1) преобразуем к эквивалентному виду x=φ(x), (3.7)
что можно сделать всегда и притом множеством способов.
Выберем начальное приближение x0Î [a;b].
Вычислим новые приближения:
x1=φ(x0)
x2=φ(x1)
………..
xi=φ(xi-1), i=1,2,… где i − номер итерации. (3.8)
Последовательное вычисление значений xi по формуле (3.8) называется итерационным процессом метода простых итераций, а сама формула - формулой итерационного процесса метода.
Если 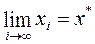 , то итерационный процесс сходящийся.
, то итерационный процесс сходящийся.
Условие сходимости 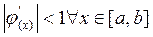 (3.9)
(3.9)
Точное решение x* получить невозможно, так как требуется бесконечный итерационный процесс.
Можно получить приближенное решение, прервав итерационный (3.8) при достижении условия
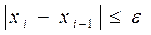 , (3.10)
, (3.10)
где ε - заданная точность; i - номер последней итерации.
В большинстве случаев условие завершения итерационного процесса (3.10) обеспечивает близость значения xi к точному решению:
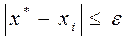
Рассмотрим геометрическую иллюстрацию метода простых итераций.
Уравнение (3.7) представим на графике в виде двух функций: y1 = x и y2= φ(x).
 Возможные случаи взаимного расположения графиков функций, и соответственно, видов итерационного процесса показаны на рис. 3.7 – 3.10.
Возможные случаи взаимного расположения графиков функций, и соответственно, видов итерационного процесса показаны на рис. 3.7 – 3.10.

Рис. 3.7 Итерационный процесс для случая 0< 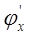 <1
<1 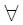 xÎ[a,b].
xÎ[a,b].
 |
Рис. 3.8 Итерационный процесс для случая -1< 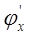 <1
<1 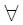 xÎ[a,b].
xÎ[a,b].
 |
Рис. 3.9 Итерационный процесс для случая 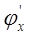 >1
>1 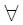 xÎ[a,b].
xÎ[a,b].
 |
Рис. 3.10 Итерационный процесс для случая 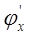 £ - 1
£ - 1 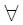 xÎ[a,b].
xÎ[a,b].
Из анализа графиков следует, что скорость сходимости растет при уменьшении значения 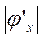
Метод достаточно прост, обобщается на системы уравнений, устойчив к погрешности округления (она не накапливается).
При разработке алгоритма решения нелинейного уравнения методом простых итераций следует предусмотреть защиту итерационного процесса от зацикливания: использовать в качестве дополнительного условия завершения итерационного процесса превышение заданного максимального числа итераций.
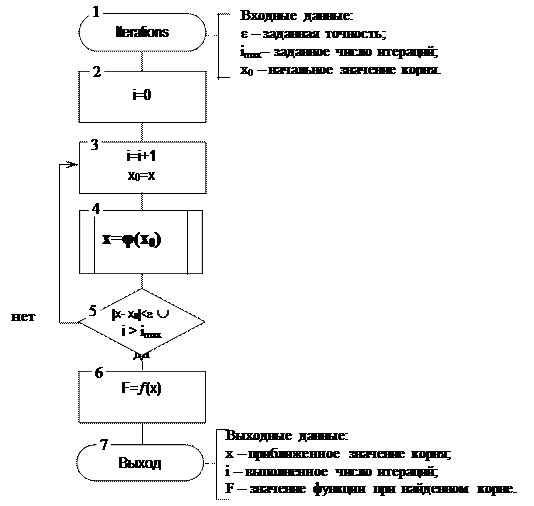 |
Рис 3.11. Алгоритм решения нелинейного уравнения методом
простых итераций:
Основной проблемой применения метода является обеспечение сходимости итерационного процесса: нужно найти такое эквивалентное преобразование (3.1) в (3.7), чтобы обеспечивалось условие сходимости (3.9).
Простейшие эквивалентные преобразования, например:
f(x) = 0 => x+f(x) = x, т.е. φ(x) = x + f(x)
или выразить явно x из (3.1)
f(x) = 0 => x - φ(x) = 0 => x = φ(x)
не гарантируют сходимость.
Рекомендуется следующий способ получения формулы сходящегося итерационного процесса.
Пусть 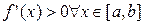 .
.
Если это не так, переписать уравнение (3.1) в виде
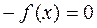
Умножить обе части уравнения на 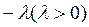 и к обеим частям прибавить x:
и к обеим частям прибавить x:
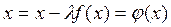
Константу l вычислить по формуле:
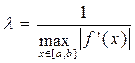 (3.11)
(3.11)
Такое значение λ гарантирует сходящийся итерационный процесс по формуле
xi = xi+1− λ f(x) (3.12)
где i=1,2,… - номер итерации, x0Î[a,b] – начальное приближение.
Пример 3.2.
Методом простых итераций уточнить корень уравнения x3=1-2 x с точностью ε=0,001. Корень отделен ранее (см. пример 3.1), x* Î [0;1].
Сначала нужно получить формулу сходящегося итерационного процесса.
Из уравнения выразим явно x:
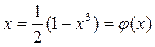
Проверим условия сходимости для полученной формулы:
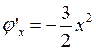 ,
, 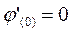 ,
, 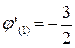
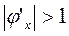 для x Î (0;1].
для x Î (0;1].
Условие сходимости не соблюдается, полученная формула не позволит уточнить корень.
Воспользуемся описанным выше способом получения формулы итерационного процесса (формулы 3.11, 3.12).
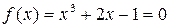 ,
, 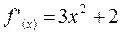 ,
, 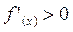 для всех x Î [0;1].
для всех x Î [0;1].
Наибольшее значение 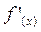 принимает при x = 1, т.е.
принимает при x = 1, т.е.
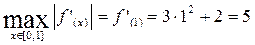
Следовательно 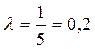 .
.
Формула сходящегося итерационного процесса
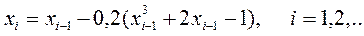
Уточним корень с помощью данной формулы.
Выберем начальное приближение на [0;1], например x0=0,5 (середина отрезка).
Вычислим первое приближение 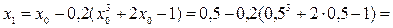
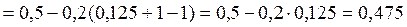
Проверим условие завершения итерационного процесса
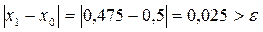
Расчет следует продолжить.
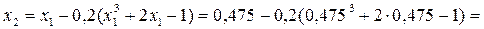
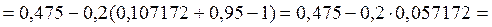
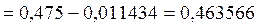
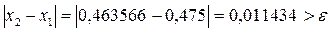
x3 = 0,458216
x4 = 0,455688
x5 = 0,454488
x6 = 0,453917 − ответ, т.к. 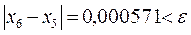
Проверим полученное значение, подставив в исходное уравнение:
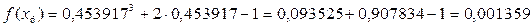
Значение f(x) близко к 0 с точностью, близкой к ε, следовательно, корень уточнен правильно.
3.2.3 Метод Ньютона (касательных).
Постановка задачи.
Дано нелинейное уравнение (3.1) f(x)=0. Корень отделен x* Î [a;b]. Требуется уточнить корень с точностью ε.
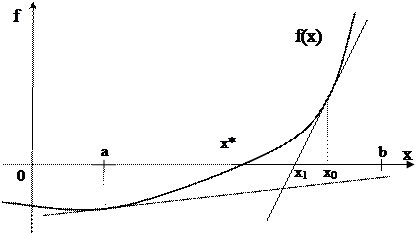
Метод основан на стратегии постепенного уточнения корня. Формулу уточнения можно получить из геометрической иллюстрации идеи метода.
 |
Рис. 3.12. Геометрическая иллюстрация метода Ньютона.
На отрезке существования корня выбирается начальное приближение x0. К кривой f(x) в точке А с координатами (x0, f(x0)) проводится касательная. Абсцисса x1 точки пересечения этой касательной с осью ОХ является новым приближением корня.
Из рисунка следует, что x1 = x0 − CB
Из ∆ABC: CD= 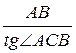 . Но
. Но 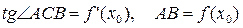 .
.
Следовательно, 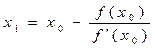
Аналогично, для i-го приближения можно записать формулу итерационного процесса метода Ньютона:
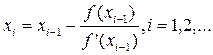 , где x0 Î [a;b]. (3.13)
, где x0 Î [a;b]. (3.13)
Условие окончания расчета: 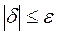 , (3.14)
, (3.14)
где 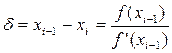 −корректирующее приращение или поправка.
−корректирующее приращение или поправка.
Условие сходимости итерационного процесса:
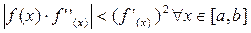 (3.15)
(3.15)
Если на отрезке существования корня знаки 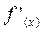 и
и 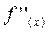 не изменяются, то начальное приближение, обеспечивающее сходимость, нужно выбрать из условия
не изменяются, то начальное приближение, обеспечивающее сходимость, нужно выбрать из условия
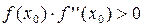 , x0Î[a;b]. (3.16)
, x0Î[a;b]. (3.16)
 т.е. в точке начального приближения знаки функций и ее второй производной должны совпадать.
т.е. в точке начального приближения знаки функций и ее второй производной должны совпадать.
Рис. 3.13. Геометрическая иллюстрация выбора начального приближения: график f(x) вогнутый, 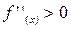 , тогда x0=b, т.к. f(b)>0.
, тогда x0=b, т.к. f(b)>0.
 Если же выбрать x0=a, то итерационный процесс будет сходиться медленнее или даже расходиться (см. касательную для x0=a).
Если же выбрать x0=a, то итерационный процесс будет сходиться медленнее или даже расходиться (см. касательную для x0=a).
●
Рис. 3.14. Геометрическая иллюстрация выбора начального приближения: график f(x) выпуклый, f ’’(x)<0, тогда x0 =a, т.к. f(a)<0.
Метод Ньютона в отличие от ранее рассмотренных методов используют свойства функции в виде значения производной, что значительно ускоряет итерационный процесс. При этом, чем больше значение модуля производной в окрестности корня (чем круче график функции), тем быстрее сходимость.
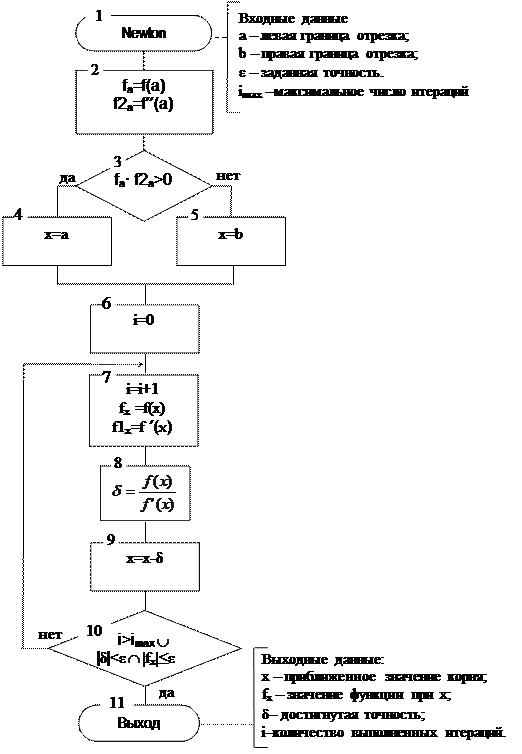 |
Рис 3.15. Схема алгоритма метода Ньютона:
Достоинства метода: высокая скорость сходимости; обобщается на системы уравнений.
Недостатки: сложный, т.к. требуется вычисление производных; сильная зависимость сходимости от вида функции и выбора начального приближения.
Пример 3.3.
Методом Ньютона уточнить корни уравнения x3 = 1− 2x с точностью ε=0,001. Корень отделён ранее (пример 3.1), x* Î [0,1].
Сначала нужно выбрать начальное приближение.
f(x) = x3+ 2 x−1
f ’(x) = 3 x2 +2
f ’’(x) = 6 x
Производные имеют постоянный знак на отрезке (0,1], поэтому для выбора начального приближения достаточно использовать условие (3.16).
Знак второй производной на отрезке положительный, следовательно
x0 = b = 1, т.к. f(b) = f(1) = 13+2·1−1 = 2 > 0
Вычислим несколько приближений:
x1 = 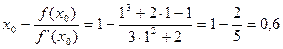
x2 = 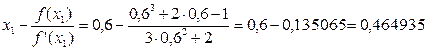
x3 =0,464935−0,011468=0,453467
x3 =0,453463−0,0000695=0,453398
Решение получено за 4 итерации, так как поправка стала меньше заданной точности: 0,0000695 < ε.
Тема 4
Решение систем линейных уравнений.
|
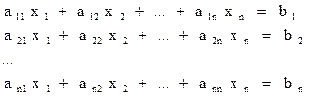 |
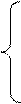 Дана система линейных уравнений (СЛУ) с n неизвестными:
Дана система линейных уравнений (СЛУ) с n неизвестными:
В матричной форме записи система (4.1) имеет вид:
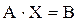 (4.2)
(4.2)
где: n – порядок системы;
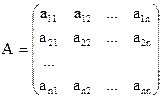 – матрица коэффициентов системы;
– матрица коэффициентов системы;
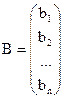 – вектор свободных членов;
– вектор свободных членов; 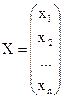 – вектор неизвестных;
– вектор неизвестных;
В свернутой форме записи СЛУ имеет вид:
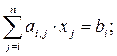
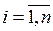 (4.3)
(4.3)
Система называется обусловленной (не вырожденной, не особенной), если определитель системы DA ¹ 0, и тогда система (4.1) имеет единственное решение.
Система называется не обусловленной (вырожденной, особенной), если DA = 0, и тогда система (4.1) не имеет решений или имеет бесконечное множество решений.
На практике коэффициенты системы aij и свободные члены bi часто задаются приближенно, с некоторой неустранимой погрешностью. Поэтому, кроме существования и единственности решения СЛУ, важно еще знать, как влияет такая погрешность на получаемое решение.
Система называется плохо обусловленной, если неустранимая погрешность оказывает сильное влияние на решение; у таких систем определитель близок, но не равен 0.
Рассмотрим пример плохо обусловленной системы.
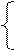 Дана система
Дана система 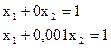
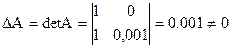
Решение 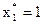 ;
; 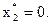
Пусть b2 имеет неустранимую погрешность 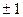 %.
%.
Если b2 = 1,01, то 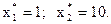
Если b2 = 0,99, то 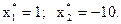
Решение изменяется очень сильно, следовательно, система плохо обусловлена, о чем говорит значение её определителя.
Рассмотрим геометрическую иллюстрацию обусловленности СЛУ на примере системы двух уравнений с двумя неизвестными:
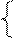 a11 x1+ a12 x2 = b1 уравнение (I)
a11 x1+ a12 x2 = b1 уравнение (I)
a21 x1+ a22 x2= b2 уравнение (II)
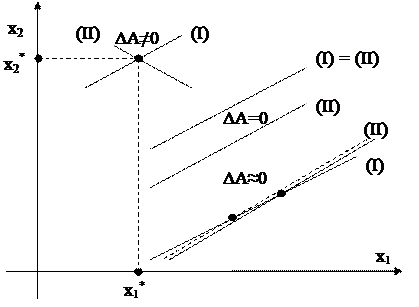 |
Рис. 4.1. Геометрическая иллюстрация обусловленности СЛУ.
Каждому уравнению в плоскости (x1,x2) соответствует прямая, а точка пересечения этих прямых является решением этой системы. Если ΔA = 0, то наклоны прямых одинаковы, и они либо параллельны (т.е. не имеют решения), либо совпадают (имеют бесконечное множество решений). Если ΔA ¹ 0, то прямые имеют единственную точку пересечения.
Но если система плохо обусловлена (∆А≈0), даже незначительное изменение одного из коэффициентов приведет к сильному изменению решения системы, т.к. прямые почти параллельны.
Для решения СЛУ широко применяться прямые и итерационные методы. Область применения некоторых из них показана в таблице.
| Тип | Название метода | Число арифметических действий (при n = 20) | Область примененения |
| Прямые | Формулы Крамера | ~ 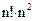 ( (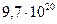 ) )
| n<5 |
| Исключения Гаусса | ~ 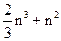 (5733) (5733)
| n<200 | |
| Итерационные | Простых итераций | ~ n² на каждой итерации (400n) | до 105 |
| Гаусса-Зейделя |
Современная супер-ЭВМ имеет производительность 30 терафлоп – 30·1012 операций с вещественными числами в секунду. Такой машине для решения СЛУ для n=20 по формуле Крамера требуется:
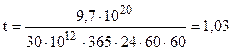 года.
года.
На решение СЛУ прямым методом сильное влияние оказывает погрешность округления, т.к. требуется огромное количество арифметических действий.
На решение СЛУ итерационным методом погрешность округления практически не влияет, но не всегда удается обеспечить сходимость итерационного процесса.
4.1. Формулы Крамера.
xi* = DAi / DA, i = 1, n, 1 (4.4)
где Ai – вспомогательная матрица, полученная из A заменой i-го столбца вектором свободных членов.
Пример 4.1. Решить СЛУ, используя формулы Крамера.
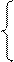 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
x1 2×x3 = -1
2×x1 - x2 – 3×x3 = 5
Вычислим определители по правилу треугольников:
DA = 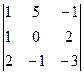 = 0 + 1 + 20 + 0 + 15 + 2 = 38 – система обусловлена.
= 0 + 1 + 20 + 0 + 15 + 2 = 38 – система обусловлена.
DA1 = 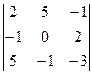 = 0 + 50 - 1 - 0 + 4 - 15 = 38
= 0 + 50 - 1 - 0 + 4 - 15 = 38
DA2 = 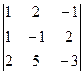 = 3 + 8 – 5 – 2 + 6 - 10 = 0
= 3 + 8 – 5 – 2 + 6 - 10 = 0
DA3 = 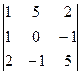 = 0 - 10 – 2 – 0 -25 - 1 = -38
= 0 - 10 – 2 – 0 -25 - 1 = -38
Вычислим решения:
x1* = DA1 / DA = 38/38 = 1;
x2* = DA2 / DA = 0/38 = 0;
x3* = DA3 / DA =-38/38 = -1.
Проверим полученное решение подстановкой в исходную систему.
1 + 5×0 – (-1) = 2
1 + 2×(-1) = -1
2×1 – 0 – 3×(-1) = 5
Система обращается в тождество, решение верное.
Формулы Крамера применяться редко, только для n≤4.
4.2. Метод исключений Гаусса.
Решим рассмотренную ранее систему (пример 4.1) методом исключения Гаусса.
Пример 3.2. Решение проводиться в два этапа.
1 этап Прямой ход - матрица A преобразуется к треугольному виду: путем эквивалентных линейных преобразований уравнений системы поддиагональные коэффициенты матрицы А обнуляются.
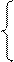 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
x1 2×x3 = -1
2×x1 - x2 – 3×x3 = 5
Исключим x1 из 2-го и 3-го уравнения: ко 2-му уравнению прибавим 1-ое, умноженное на (-1); к 3-му уравнению прибавим 1-ое, умноженное на (-2).
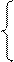 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
- 5×x2 + 3×x3 = -3
- 11×x2 – x3 = 1
Исключим x2 из 3-го уравнения: к 3-му уравнению прибавим 2-ое, умноженное на (-11/5). Полученный вид системы после прямого хода
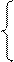 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
- 5×x2 + 3×x3 = -3
– 38/5×x3 = 38/5
2 этап Обратный ход - вычисляются значения неизвестных, начиная с последнего уравнения:
x3* = -1
-5×x2 + 3×x3*=-3 Þ x2*=(3 + 3×x3*)=(3 + 3×(-1))=0
x1 +5×x2* - x3*=2 Þ x1*=2 + 5×x2* + x3*=2 + 5×0 + (-1)=1
Полученное решение нужно обязательно проверить, подставив в исходную систему!
Словесное описание алгоритма метода исключения Гаусса. Схема алгоритма приведена на рисунках 4.1-4.6.
Алгоритм прямого хода:
Шаг 1. Примем k=1
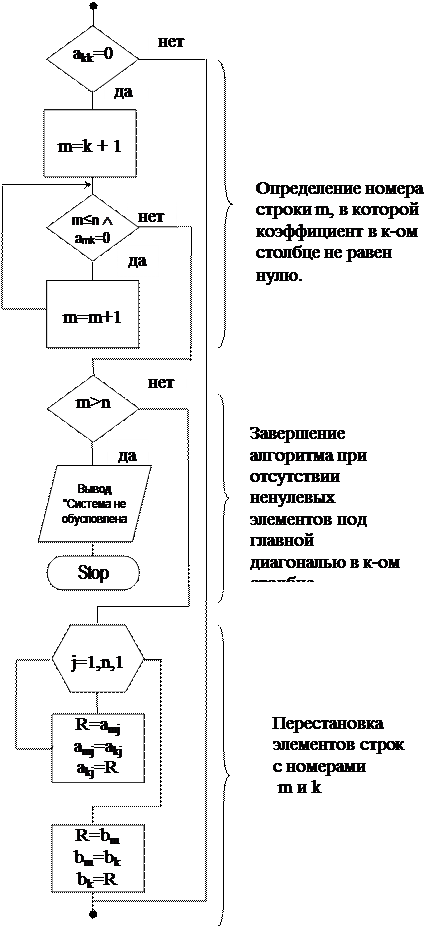
Шаг 2. Выбираем рабочую строку.
Если akk ≠ 0, то k-ая строка – рабочая.
Если нет, меняем k-ю строку на m-ю (n≥m>k), в которой amk ≠ 0, 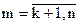 . Если такой строки нет, система вырожденная, решение прекратить.
. Если такой строки нет, система вырожденная, решение прекратить.
Шаг 3. Для строк i=k+1, k+2, …, n вычисляются новые значения коэффициентов.
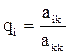 ,
, 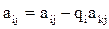 ,
, 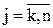 и новые правые части
и новые правые части 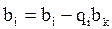
Шаг 4. Увеличиваем k = k + 1. Если k = n, прямой ход завершен, иначе алгоритм повторяется со второго шага.
Получаем верхнюю треугольную матрицу А:
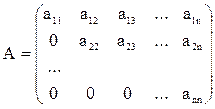 ,
, 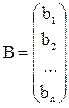
Алгоритм обратного хода:
Шаг 1. Вычислим 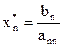
Шаг 2. Вычислим:
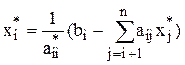 ,
, 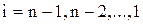
 |
Рис. 4.1. Основной алгоритм решения СЛУ методом исключения Гаусса.
Для контроля правильности решения нужно считать невязки δi по формуле (4.5).
δi 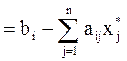 ,
, 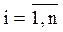 (4.5)
(4.5)
Если невязки велики, задача решена неверно. Причиной может быть сбой машины (крайне редко), ошибки в программе, погрешность округления (при большом n и когда DA = detA = 0- система плохо обусловлена).
Разновидности метода исключения:
а) Метод исключения Гаусса с выбором главного элемента в столбце.
В алгоритме прямого хода на шаге 2 рабочая строка выбирается из условия
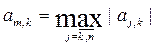 ,
,
т.е. рабочей выбирается та строка, в которой находится наибольший по модулю коэффициент k-го столбца, расположенный на главной диагонали и под ней.
б) Метод Гаусса-Жордана.
В алгоритм прямого хода нужно внести следующие изменения:
- на шаге 3 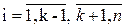
- на шаге 4 прямой ход завершиться при достижении условия k>n.
Вид матрицы коэффициентов после прямого хода
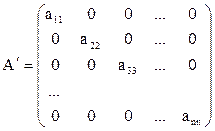
Упрощается обратный ход: xi =bi / ai,i, i =1,2,…,n
Недостаток метода – увеличение общего числа действий, и соответственно, влияния погрешности округления.
 | |||
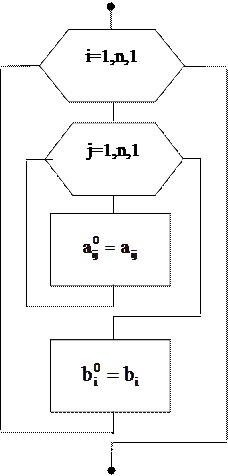 | |||
Рис. 3. Алгоритм запоминания коэффициентов.
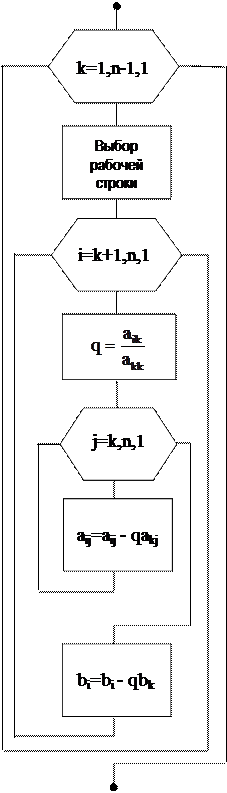
Рис. 4.2. Алгоритм прямого хода
 | |||
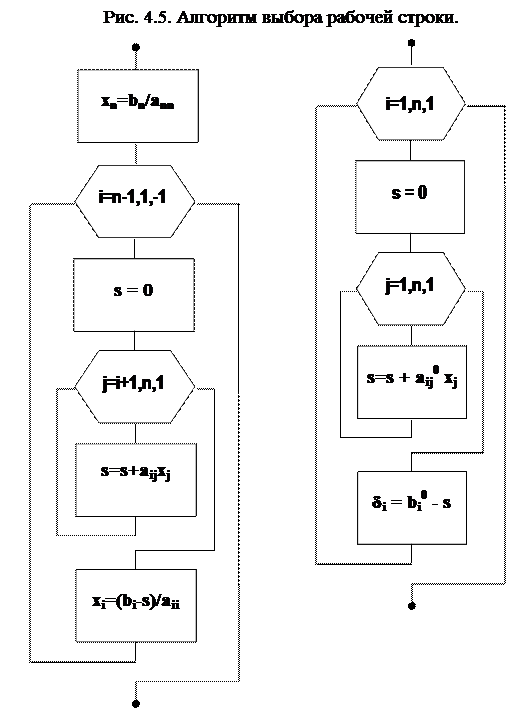 |
Рис. 4.6. Алгоритм расчета невязок
Рис. 4.5. Алгоритм обратного хода.
Нужно подчеркнуть, что для вычисления значения определителя квадратной матрицы можно использовать алгоритм прямого хода: для треугольной или диагональной квадратной матрицы определитель равен произведению элементов главной диагонали.
4.3. Метод простых итераций.
Рассмотрим особенности решения СЛУ методом простых итераций на примере.
Пример 4.3. Требуется найти решение системы с точностью ε=0,001.
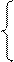 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
x1 2×x3 = -1
2×x1 - x2 – 3×x3 = 5
Приведем систему к новому, каноническому виду метода простых итераций. Для этого нужно преобразовать исходную систему так, чтобы в каждой строке новой матрицы А коэффициент, расположенный на главной диагонали, превышал по абсолютной величине сумму абсолютных значений остальных коэффициенты в этой сроке.
При выполнении эквивалентных линейных преобразований системы нужно соблюдать следующие требование: каждое уравнение исходной системы должно участвовать хотя бы в одном преобразовании.
В первом уравнении исходной системы коэффициент при х2 больше суммы модулей других коэффициентов: 5> 1+1. Поэтому это уравнение в новой системе нужно записать вторым уравнением. Для получения нового первого уравнения можно второе уравнение умножить на 2 и сложить с третьим уравнением. Для получения нового третьего уравнения можно из третьего уравнения вычесть второе.
В итоге описанных преобразований получиться следующая система:
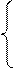
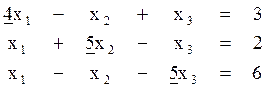
Важно отметить, что подобные преобразования не меняют решения системы.
Выразим явно из каждого нового уравнения очередное неизвестное – получим формулы итерационного процесса.
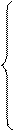
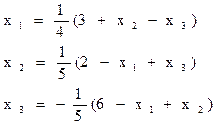
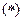
Возьмем любое начальное приближение 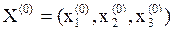 , например
, например 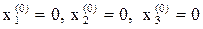 .
.
Вычислим новое приближение решения 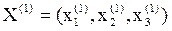 , подставив в правую часть
, подставив в правую часть 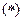 начальное приближение:
начальное приближение:
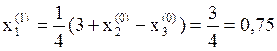
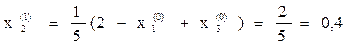
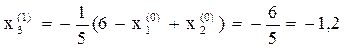
Оценим достигнутую точность δ по формуле:
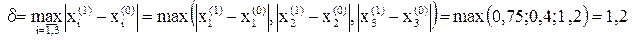
Итерационный процесс нужно продолжить, т.к. δ > ε.
Вычислим второе приближение 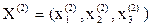 , подставив в правую часть
, подставив в правую часть 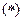 первое приближение:
первое приближение:
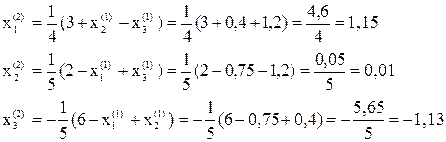
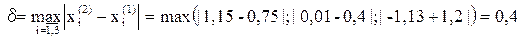
Третье приближение:
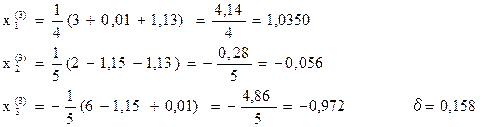
Четвертое приближение:
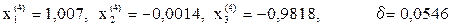
Очевидно, что итерационный процесс сходиться, т.к. значение δ монотонно убывает. Для достижения требуемой точности ε=0,001 потребуется еще несколько итераций.
Скорость сходимости зависит от уровня преобладания значений диагональных коэффициентов.
Основные расчетные зависимости метода простых итераций:
Формула итерационного процесса:
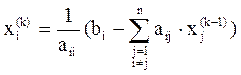 ,
, 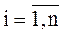 (4.6)
(4.6)
где: k = 1, 2, … – номер приближения.
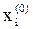 – начальное приближение,
– начальное приближение, 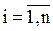 ;
;
Условия завершения итерационного процесса:
d£e (4.7)
где e – требуемая точность;
d – оценка достигнутой точности, 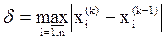 (4.8)
(4.8)
или 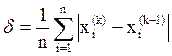 (4.9)
(4.9)
Условие сходимости итерационного процесса (условие преобладания диагональных коэффициентов):
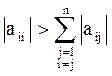
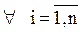 (4.10)
(4.10)
Схема алгоритма метода представлена на рис. 4.7.
Если в полученных результатах значения δ > e и k > kmax, то задача не решена, т.е. x(1:n) не является решением системы. Необходимо проверить условия сходимости или увеличить kmax.
4.4 Метод Гаусса-Зейделя
В формуле итерационного процесса метода простых итераций (4.6) к моменту вычисления xi(k) уже вычислены значения x1(k),x2(k),...,xi-1(k).
Очевидно, что эти значения в большинстве случаев ближе к решению и их можно использовать для вычисления xi(k). Исходя из этого, Гаусс и Зейдель предложили видоизмененную формулу итерационного процесса
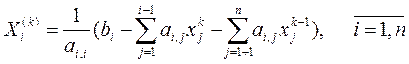 (4.11)
(4.11)
Условие завершения итерационного процесса (4.7) и условия сходимости (4.10) справедливы и для данного метода. Поэтому схема алгоритма Гаусса-Зейделя отлична только формулой расчета нового приближения:
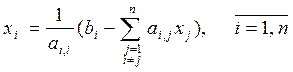
Метод этот, как правило, позволяет достичь требуемой точности ε за меньшее число итераций, т.е. имеет лучшую сходимость.
Достоинства итерационных методов:
1. Погрешность округления не накапливается от итерации к итерации.
2. Число итераций при n>100 обычно меньше n, поэтому общее число действий меньше n3, т.е. меньше, чем в методе исключений Гаусса.
3. Не требуется больший объем памяти.
4. Итерационные методы особенно выгодны для систем с большим количеством нулевых коэффициентов (систем с разряженной итерацией). Методы исключения наоборот: чем больше нулей, тем чаще требуется выбирать новую рабочую строку.
Недостаток - не всегда можно обеспечить сходность итерационного процесса. С увеличением размерности системы труднее выполнить линейные преобразования для обеспечения сходимости.
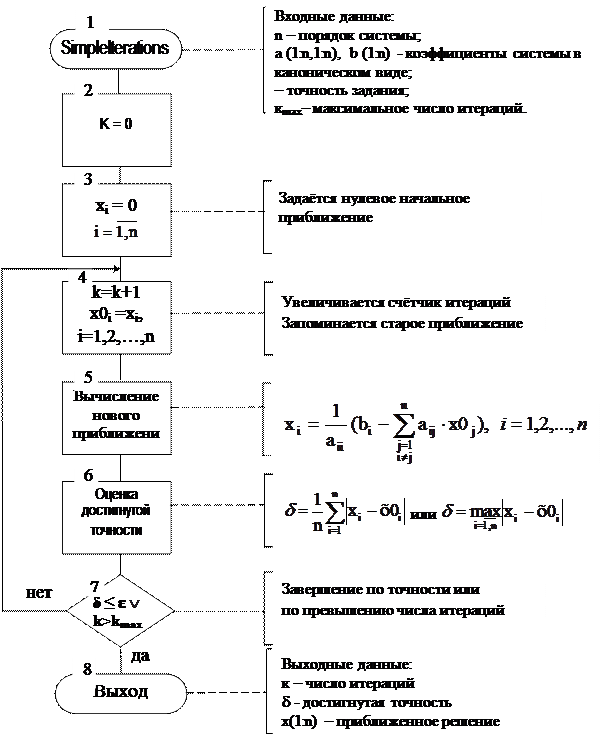 |
Рис. 4.7. Схема алгоритма метода простых итераций
Тема 5
Решение систем нелинейных уравнений (СНУ).
При моделировании задача нахождения решения системы алгебраических или трансцендентных уравнений является распространенной вычислительной задачей. Например, к решению таких систем сводятся расчеты фазового и химического равновесия многокомпонентных смесей, расчеты статических режимов многих технологических процессов и др.
Запишем систему n нелинейных уравнений с n неизвестными (СНУ) в общем виде:
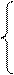 f1(x1, x2, …, xn) = 0
f1(x1, x2, …, xn) = 0
f2(x1, x2, …, xn) = 0 (5.1)
…
fn(x1, x2, …, xn) = 0
Эту систему можно записать в компактной, операторной форме:
F(X) = 0 (5.2)
где
|
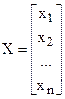
|
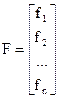
Решением системы называется набор значений 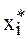 ,
, 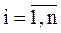 (вектор X*), при которых все функции fi равны 0 (система (5.1) обращается в тождество.)
(вектор X*), при которых все функции fi равны 0 (система (5.1) обращается в тождество.)
СНУ могут иметь единственное решение, множество решений или вообще не иметь его. Поэтому численное решение СНУ проводят в два этапа:
1 этап – отделение решений.
2 этап – уточнение всех или только нужных решений.
5.1. Отделение решений.
Отделить решения – значит установить количество решений, определить приближенные значения каждого из них или указать область, в которой решение существует и является единственным.
Задача отделения решений достаточно просто решается только для системы двух уравнений с двумя неизвестными.
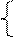 f1(x1, x2) = 0
f1(x1, x2) = 0
f2(x1, x2) = 0
Для этого необходимо в координатах (x1, x2) построить кривые
f1(x1,х2) = 0, f2(x1,х2) = 0.
Точки пересечения этих кривых являются решениями системы. Так как координаты точек пересечения определяются приближенно, целесообразно говорить об области существования решения D. Эта область задается интервалами по каждой координате, внутри которых находятся искомые значения неизвестных.
 |
Рис. 5.1. Графическое отделение решений СНУ.
Для систем с большим числом неизвестных (n ³ 3) удовлетворительных общих методов определения области существования решения нет. Поэтому при решении СНУ эта область обычно определяется при анализе решаемой задачи, например, исходя из физического смысла неизвестных.
Отделение решений позволяет:
1. Выявить число решений и область существования каждого из них.
2. Проанализировать возможность применения выбранного метода решения СНУ в каждой области.
3. Выбрать начальное приближение решения X(0) из области его существования, так что X(0)ÎD.
При отсутствии информации об области существования решения СНУ выбор начального приближения X(0) проводиться методом проб и ошибок (методом “тыка”).
Пример 5.1. Отделить решения системы
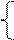 x2 + y2=1
x2 + y2=1
ln(x)+2y=-1
Запишем систему в стандартном виде (5.1).
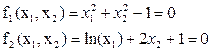
Область определения функций
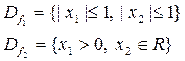
Очевидно, что решения могут быть только в общей области определения этих функций.
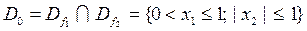
Решения существуют, т.к. D0 ≠ Æ.
Для отделения решения нужно построить графики функций в общей области определения.
График первой функции – окружность единичного радиуса с центром в начале координат.
Для построения графика второй функции нужно вычислить значение
 2015-02-18
2015-02-18 616
616







