2015-02-18
411
Задача. При испытании на крепость отобраны в случайном порядке 400 отрезков пряжи одиночной нити (основа – 65 кордная) были получены следующие результаты[20]:
Таблица 19
Расчет основных выборочных характеристик (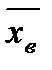
и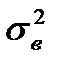 
).
Крепость пряжи (гр.)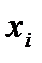 
| Число испытанных образцов m |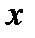 
(середина интервала)
| 
| 
| 
| 
|
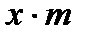
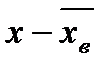
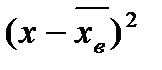
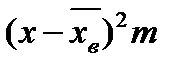
| A |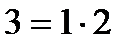 
| 
| 
| 
| ||
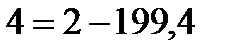
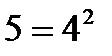
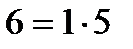
| 105-125 | -84,4 | 7123,36 | 56986,88 | |||
| 125-145 | -64,4 | 4147,36 | 99536,64 | |||
| 145-165 | -44,4 | 1971,36 | 78854,4 | |||
| 165-185 | -24,4 | 595,36 | 21432,96 | |||
| 185-205 | -4,4 | 19,36 | 2013,44 | |||
| 205-225 | 15,6 | 243,36 | 29203,2 | |||
| 225-245 | 35,6 | 1267,36 | 44357,6 | |||
| 245-265 | 55,6 | 3091,36 | 61827,2 | |||
| 265-285 | 75,6 | 5715,36 | 40007,52 | |||
| 285-305 | 95,6 | 9139,36 | 54836,16 | |||
| Итого |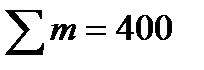 
| 
|
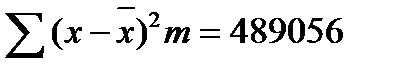
Определите с вероятностью 0,97 среднюю крепость пряжи во всей партии.
Для определения основных характеристик (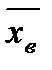 и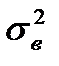 
) выборочной совокупности необходимо найти графы с 3-ей по 6-ую в таблице 19.
Выборочная средняя крепость пряжи равна:
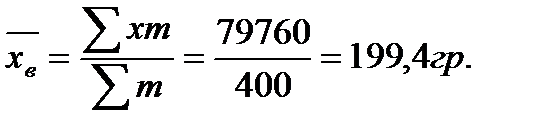
Выборочная дисперсия составляет:
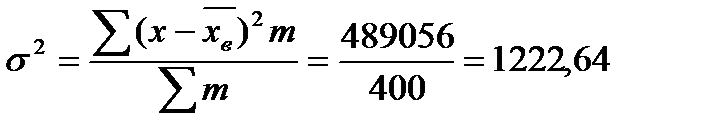
Итак, на основе следующих данных определим среднюю крепость пряжи во всей партии.
|
|
|
Дано:
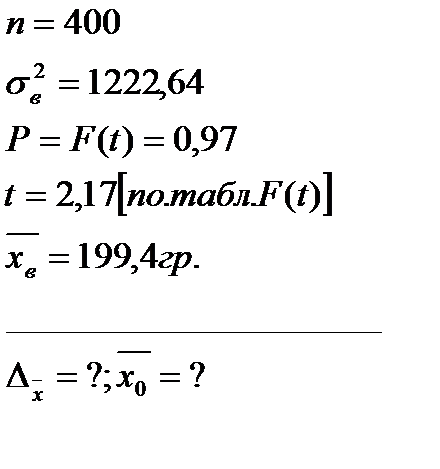[21]
Решение:
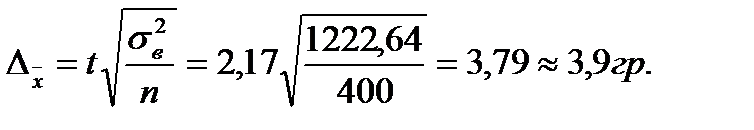
Тогда средняя крепость пряжи во всей партии будет находиться в следующих пределах:
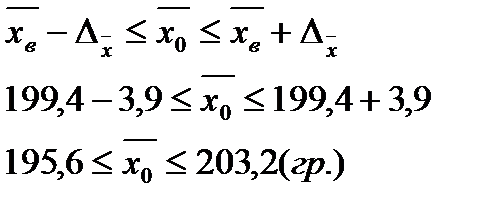
Вывод: С вероятностью 0,97 можно утверждать, что средняя крепость во всей пряжи в генеральной совокупности будет не менее 195,6 гр. и не более 203,2 гр.
