Разветвляющиеся алгоритмы. Команда ветвления

Существует широкий круг задач, при решении которых необходимо сделать определенный выбор в зависимости от выполнения некоторых условий. Процесс решения таких задач описывается алгоритмом, тип которого определяется как ветвящийся (разветвляющийся). В разветвляющихся алгоритмах принцип линейного автоматического перехода от команды к команде, от действия к действию в порядке естественного следования не является всеобщим, так как иногда возникает необходимость произвольного перехода к предписанию, то есть нарушения линейности переходов. Ветвящиеся алгоритмы допускают два способа представления - графический и словесный.

При графическом представлении алгоритма ветвление (развилка, выбор дальнейших действий) организуется с помощью логического элемента (ромб с записанным внутри условием), имеющего один вход и несколько (в простейшем случае - два) выходов. Назначение логического элемента - проверка заданного условия. В зависимости от выполнения (истинности) или невыполнения (ложности) проверяемого условия возможен выход соответственно на ветвь "Да" или "Нет". Пример:

Задача: вычислить y=|x|.

Дано: х – значение аргумента.

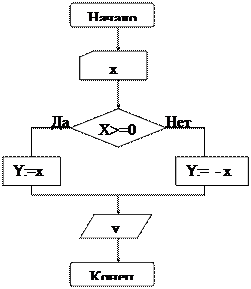
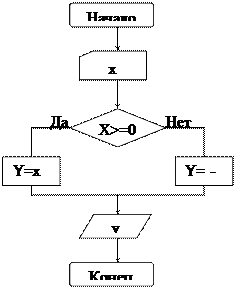Требуется: у – значение функции. Связь: y =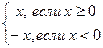

Словесное представление:

Прочесть значение x.

Если х>=0 то

y:= х

иначе

у:=– х

Конец ветвления

Записать значение у

Упражнение. Какое значение примет Z в результате выполнения алгоритма

X:=3; Y:=4

ЕСЛИ X>Y, ТО Z:=X*X+Y

ИНАЧЕ Z:= Y*Y+X

Конец ветвления

Z:=2*Z

Вид получившейся графической схемы объясняет, почему алгоритм, соответствующий ей, назвали ветвящимся. Кроме того, на схеме наглядно проявляется важное свойство ветвящихся алгоритмов: их исполнение всегда проходит только по одному из возможных путей, который определяется конкретными текущими условиями, причем в каждом случае от начала алгоритма (входа) до его конца (выхода). Это свойство присуще всякому логически правильно составленному алгоритму и является признаком правильной организации ветвлений.

Составляя алгоритм решения задачи о вычислении абсолютной величины заданного значения переменной, мы получили так называемую полную условную конструкцию. Общий вид полной условной конструкции, реализующей ветвление при графическом представлении алгоритма, изображен на рисунке

Здесь Q - проверяемое условие; P₁, P₂, …, P_n - действия, которые должны быть выполнены в случае истинности условия Q (положительная ветвь ветвления); T₁, T₂, …, T_m - действия, выполняемые, если условие Q ложно (отрицательная ветвь ветвления).

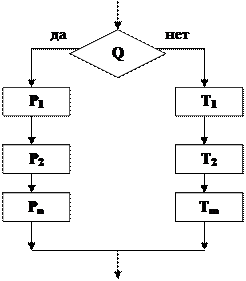При словесном представлении алгоритма полная условная конструкция реализуется командой ветвления вида:

Если Q то

P₁

P₁

…

P_n

иначе

T₁

T₂

…

T_m

Конец ветвления