2015-03-20
643
Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академика Колмогорова, совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. Или иначе: При большом числе случайных величин их средней результат перестает быть случайным и может быть предсказан с большой степенью определенности.
Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
| Наименование показателя | Вид выборки | |
| повторная | бесповторная | |
| Случайная выборка Средняя (стандартная) ошибка |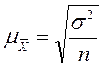 
| 
|
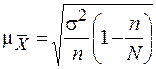
| Средняя ошибка доли признака |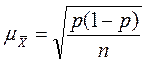 
| 
|
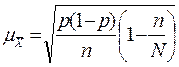
| Объем выборки |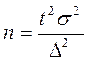 
| 
|
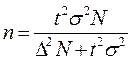
| Типическая выборка Средняя ошибка |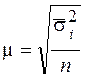 
| 
|
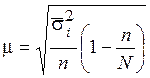
| Объем выборки |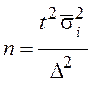 
| 
|
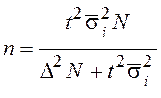
| Серийная выборка Средняя ошибка |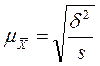 
| 
|
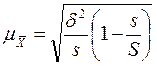
| Объем выборки |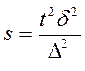 
| 
|
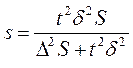
Величина ошибки зависит от колеблемости признака в генеральной совокупности и от объема выборки. Т.е. чем больше вариация, тем больше ошибка, чем больше выборка, тем меньше ошибка. Величину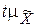 
называют предельной ошибкой выборки. Следовательно, предельная ошибка выборки 
, т.е. предельная ошибка равна t -кратному числу средних ошибок выборки.
t – коэффициент доверия
n – объем выборки;
N – объем генеральной совокупности;
s - число отобранных серий;
S – общее число серий;
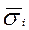- средняя из групповых дисперсий;
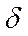- межгрупповая дисперсия.
Цель практического занятия:
уметь:
- формировать выборочную совокупность;
- определять объем выборочной совокупности;
- рассчитывать среднюю и предельную ошибки выборки.
Рекомендуемая литература:
Статистика. Под ред. В.С. Мхитаряна, с. 143-181.
Практикум по теории статистики. Под ред. Проф. Р.А. Шмойловой, с. 105 – 110.
Пример
Исходя требований ГОСТа необходимо установить оптимальный размер выборки из партии изделий 2000 штук, чтобы с вероятностью 0,997 предельная ошибка не превысила 3% от веса 500 гр. Изделия (батона).
