Степенью свободы механизма называется независимое перемещение одного или нескольких звеньев его кинематической цепи относительно стойки.
В инженерной практике различают два типа механической системы: механизм и конструкция. Механизм имеет хотя бы одну степень свободы, тогда как конструкция обладает нулевым либо отрицательным числом степеней свободы. При проектировании и изготовлении механизма важно обеспечить требуемое число его степеней свободы; при проектировании и изготовлении жесткой конструкции, напротив, важно не допустить возникновения степеней свободы и превращения конструкции в механизм.
Для определения числа степеней свободы по схемам механизмов существуют так называемые универсальные структурные формулы. Пусть имеется механизм, число звеньев которого равно n и в нем есть кинематические пары всех пяти классов. Так как в механизме всегда есть стойка, то число подвижных звеньев 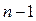 . Наибольшее возможное число степеней свободы такой системы в пространстве составит
. Наибольшее возможное число степеней свободы такой системы в пространстве составит 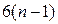 . Если считать, что связи в кинематических парах – независимые, то общее число связей, ограничивающих перемещение звеньев, выразится равенством:
. Если считать, что связи в кинематических парах – независимые, то общее число связей, ограничивающих перемещение звеньев, выразится равенством:
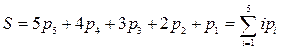 ,
,
где i – класс кинематической пары, pi – число кинематических пар, имеющих класс i. Тогда число степеней свободы механизма определится в виде разности:
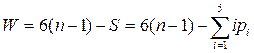 .
.
Полученное равенство известно в теории механизмов под названием структурная формула Сомова – Малышева.
Задача 1
Определить число степеней свободы манипулятора, схема которого изображена на рис. 6.
Решение
Манипулятор содержит 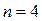 звена, имеет две вращательные и одну поступательную кинематические пары. Все указанные пары имеют пятый класс, поэтому
звена, имеет две вращательные и одну поступательную кинематические пары. Все указанные пары имеют пятый класс, поэтому 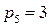 и
и 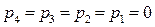 . Тогда число степеней свободы манипулятора
. Тогда число степеней свободы манипулятора
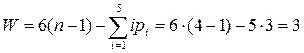 .
.
Задача 2
Определить число степеней свободы плоского шарнирного четырехзвенного механизма (рис. 7,а).
Решение
Механизм содержит четыре звена и четыре вращательные кинематические пары: 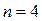 ,
, 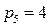 ,
, 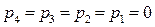 . Число степеней свободы механизма
. Число степеней свободы механизма
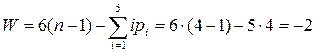 .
.
Полученный результат означает, что четырехзвенник с произвольно ориентированными в пространстве осями шарниров является не механизмом, а дважды статически неопределимой конструкцией. Для возникновения одной степени свободы требуется, чтобы три независимые связи в механизме стали повторяющимися (избыточными). Это достигается обеспечением параллельности осей шарниров, т.е. механизм должен быть обязательно плоским.
Для плоских механизмов существует структурная формула Чебышева:
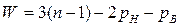 ,
,
где pH – число низших, pB – число высших кинематических пар. Решая задачу 2 по формуле Чебышева (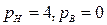 ), получим
), получим
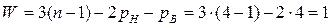 .
.
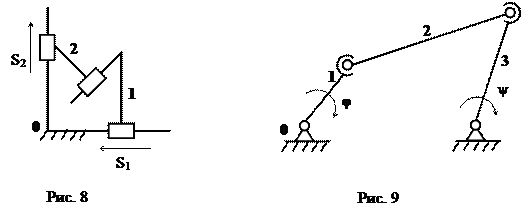
Существуют плоские механизмы, в которых звенья кинематической цепи движутся только поступательно. Такие механизмы называют клиновыми: наиболее часто они используются в ригельных замках. Схема трехзвенного клинового механизма изображена на рис. 8.
 |
Для определения числа степеней свободы клиновых механизмов используется структурная формула Добровольского:
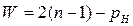 .
.
Число степеней свободы механизма (Рис. 8): 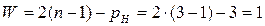 .
.
 2015-03-07
2015-03-07 3474
3474
