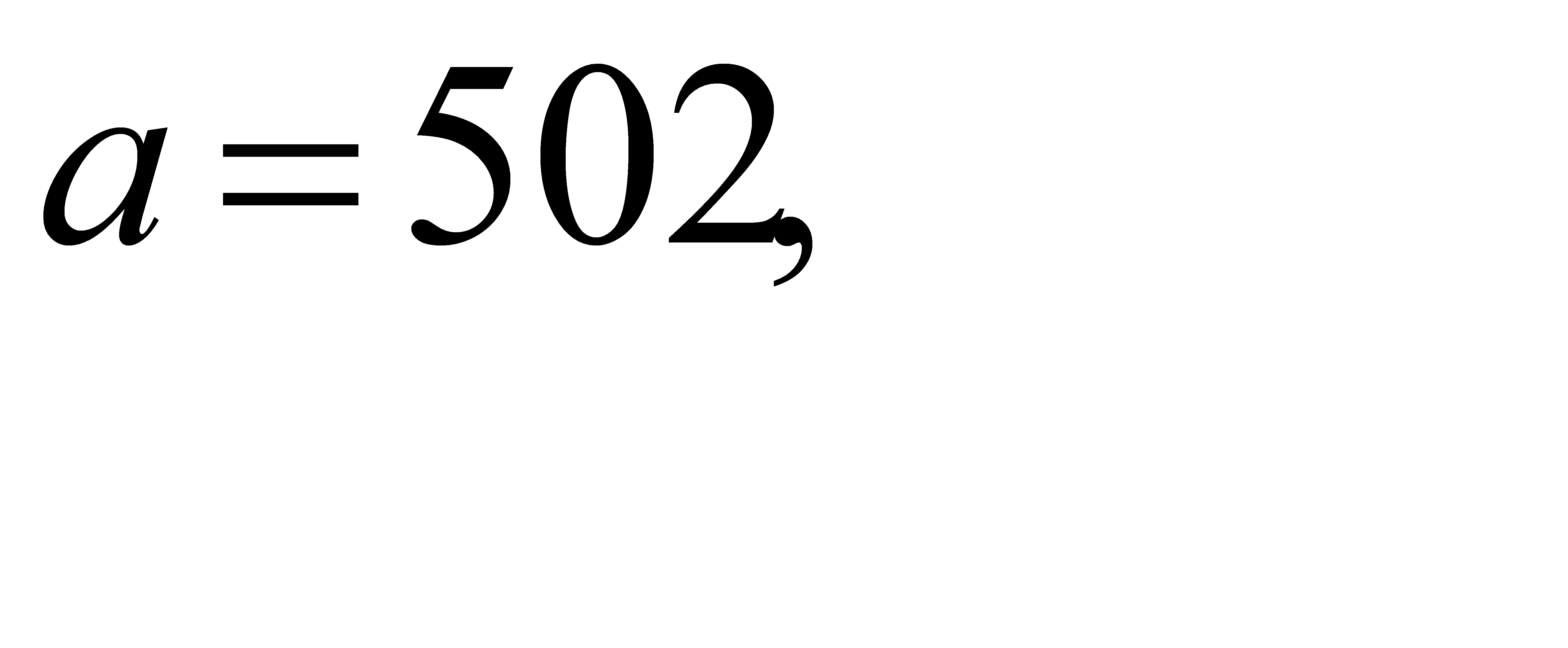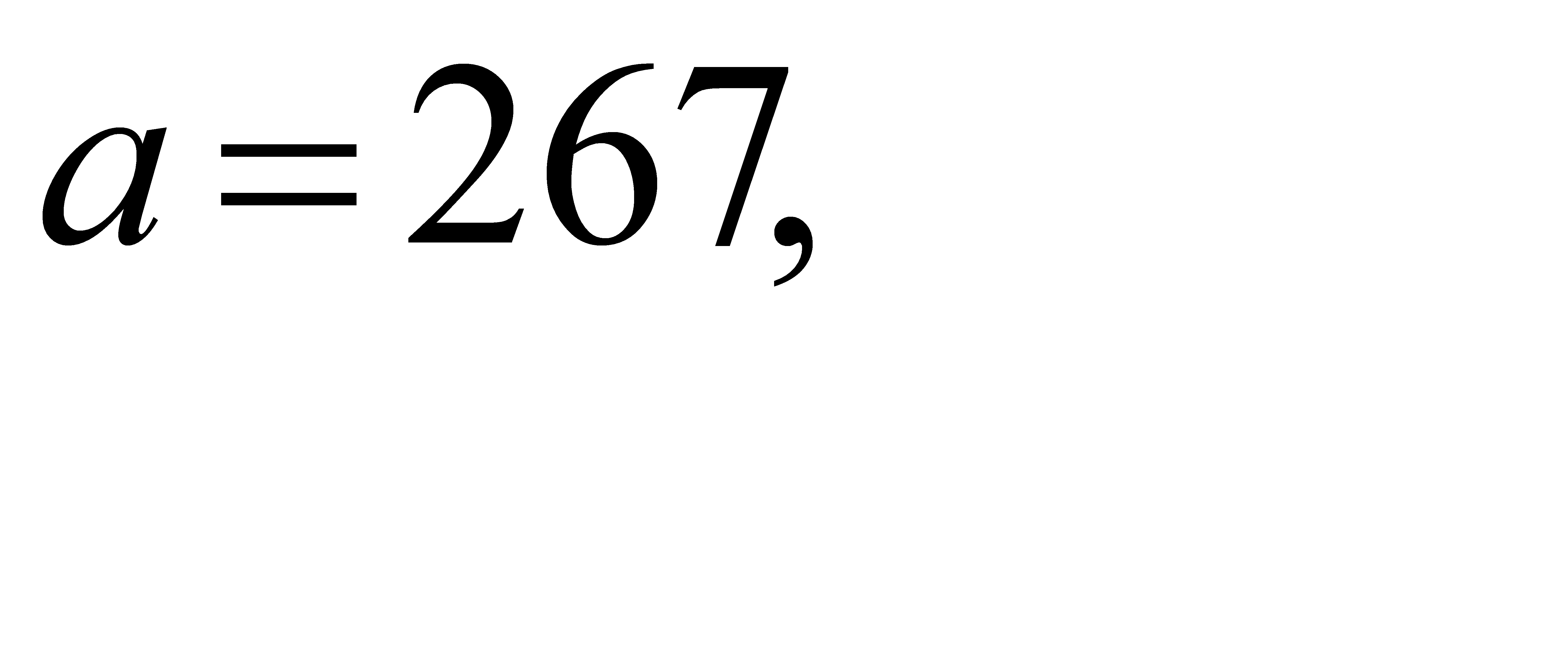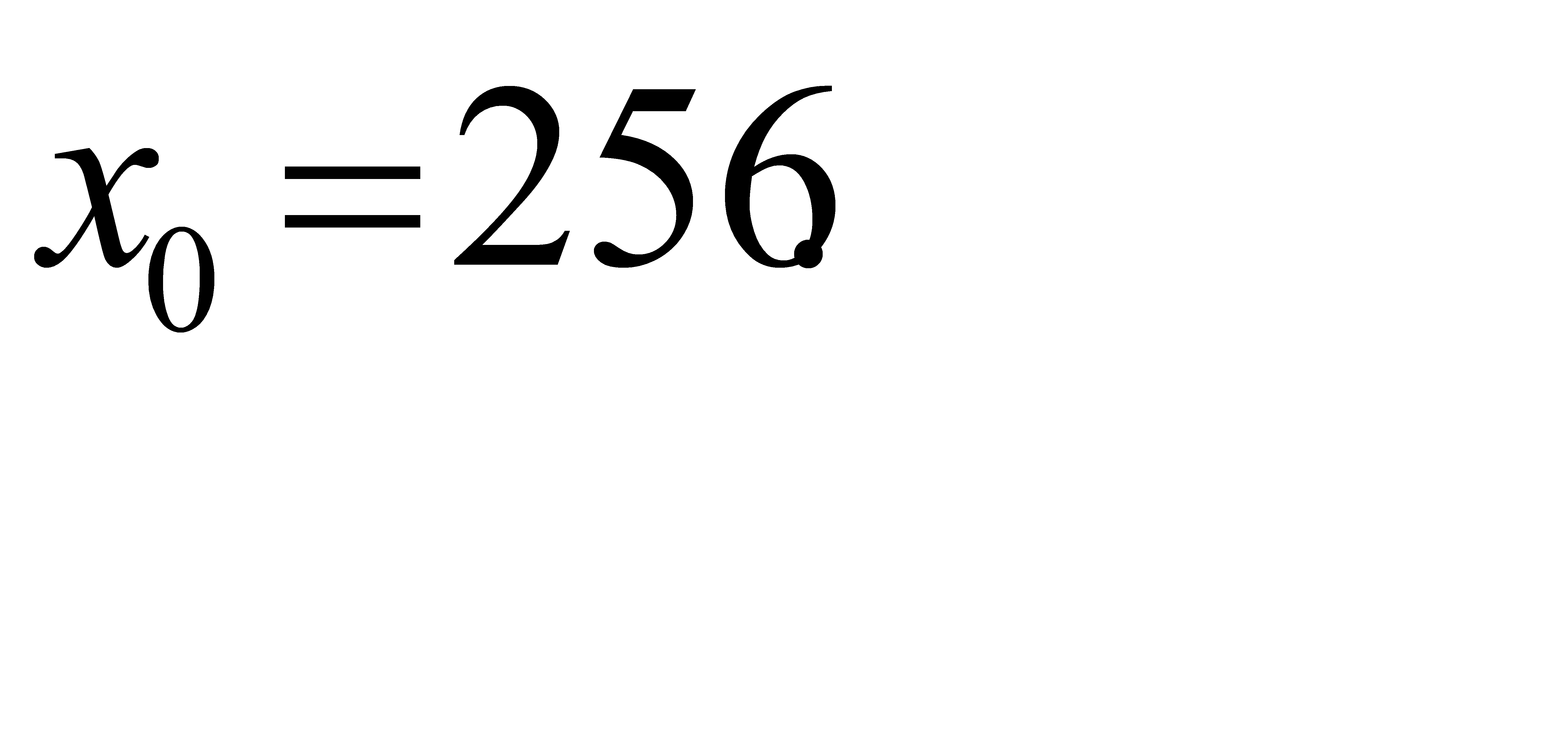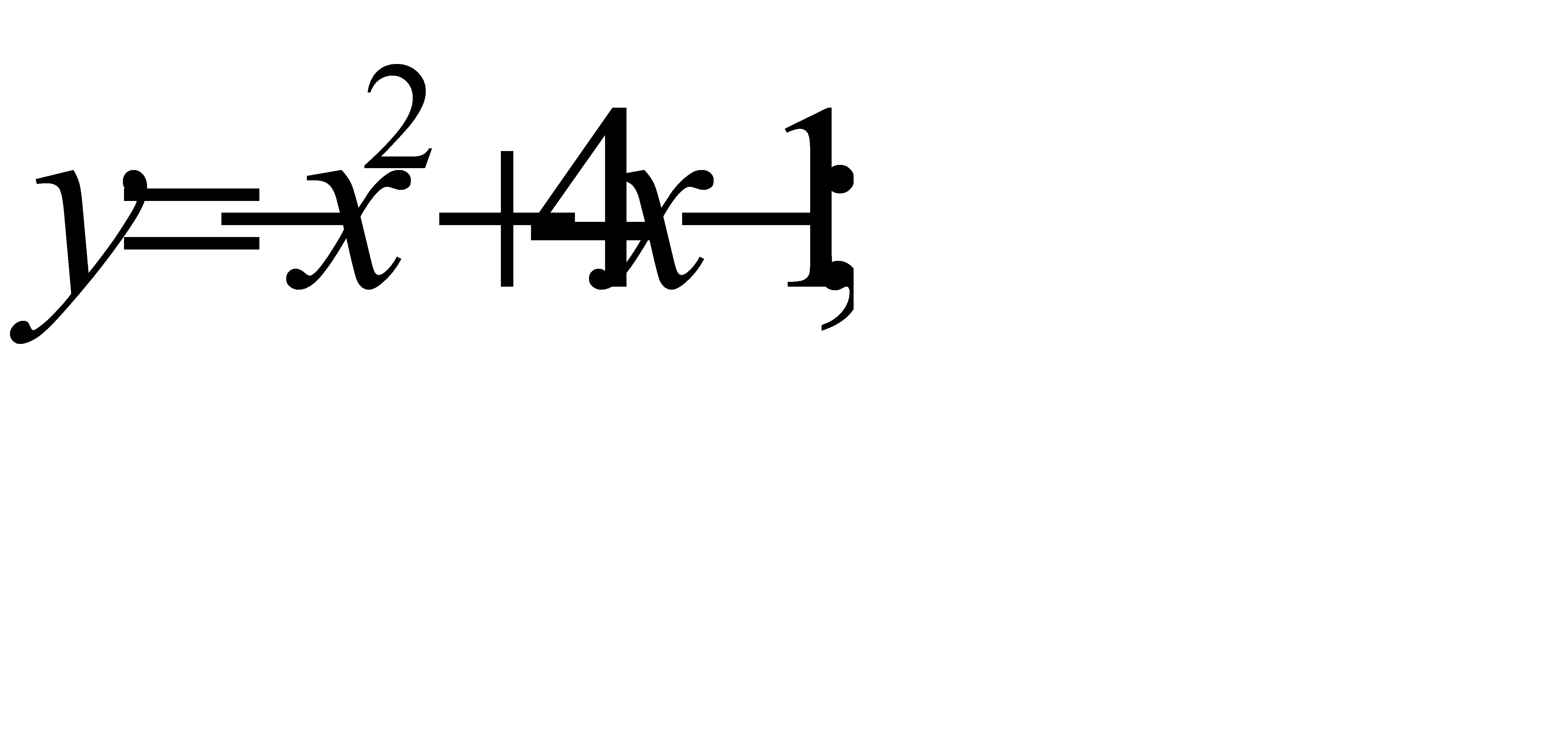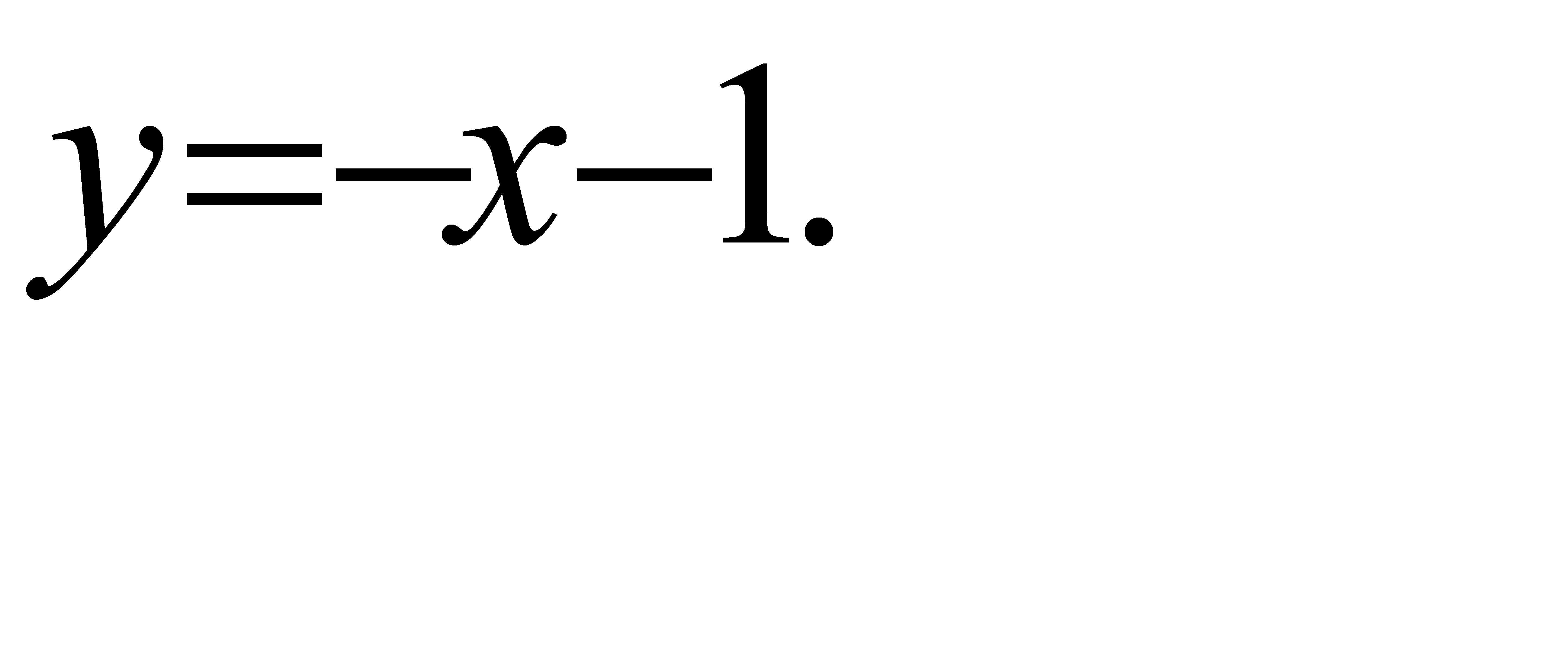1-10. Найти пределы функций.
1. 1) 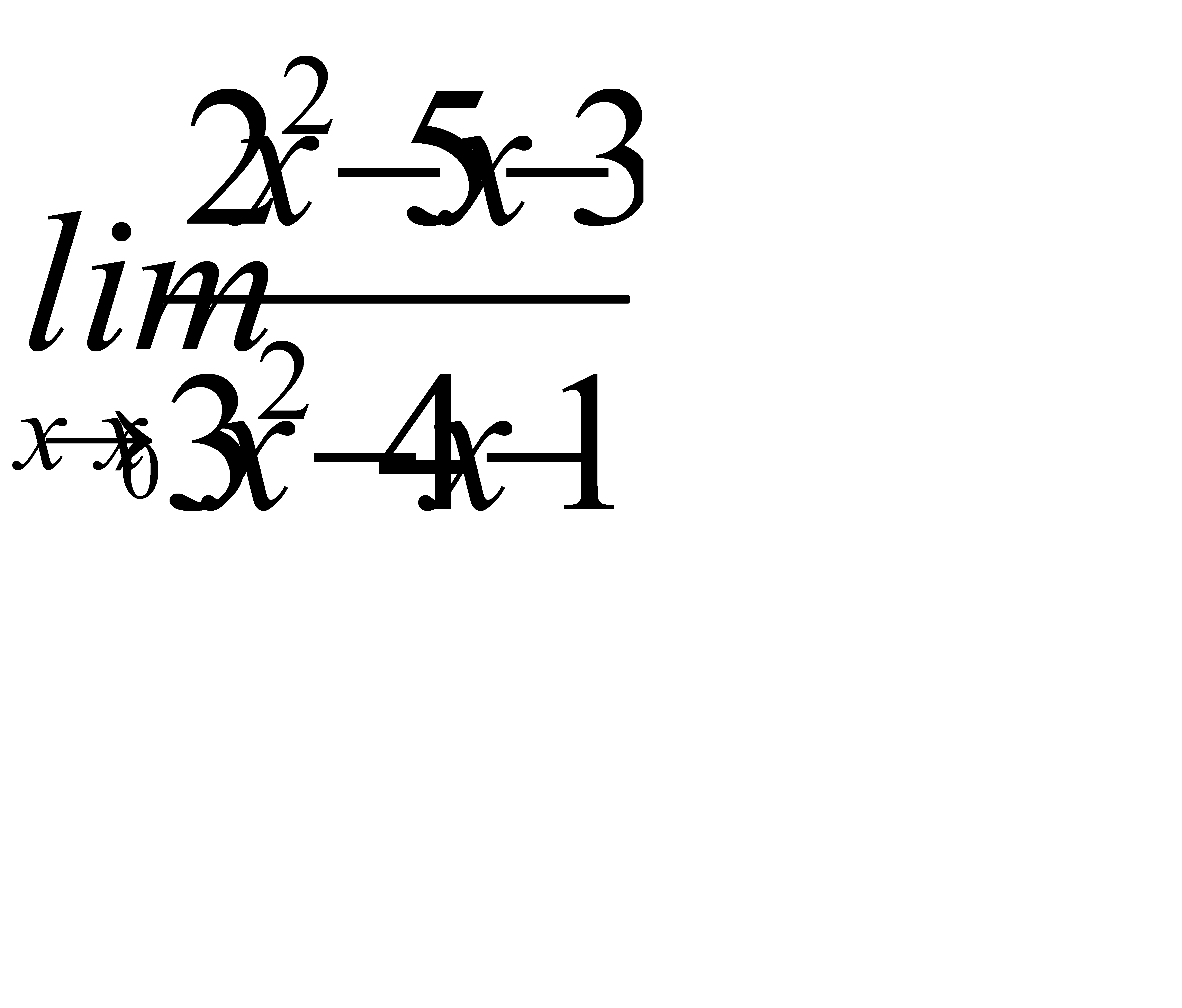 при a)
при a) 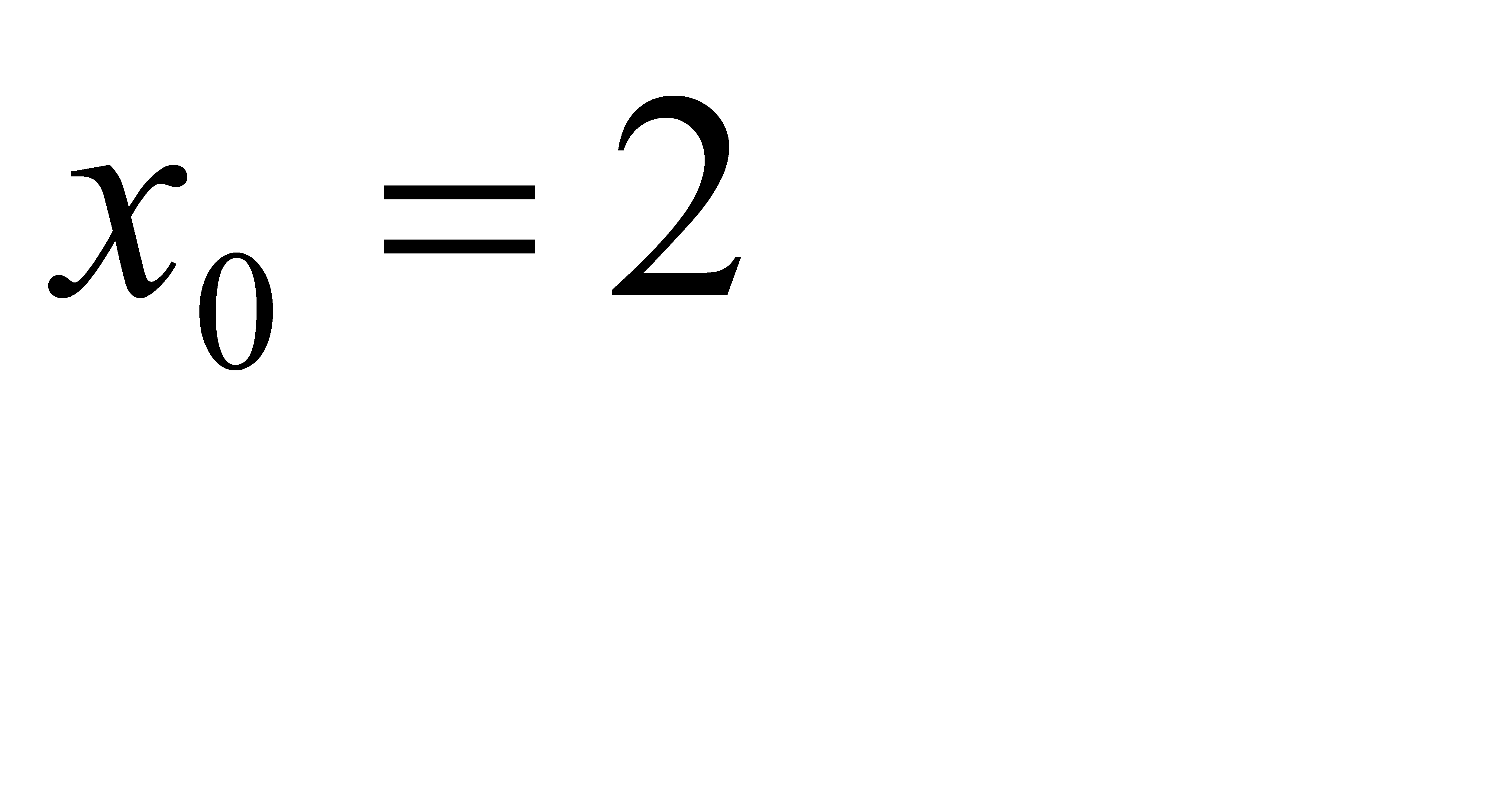 , b)
, b) 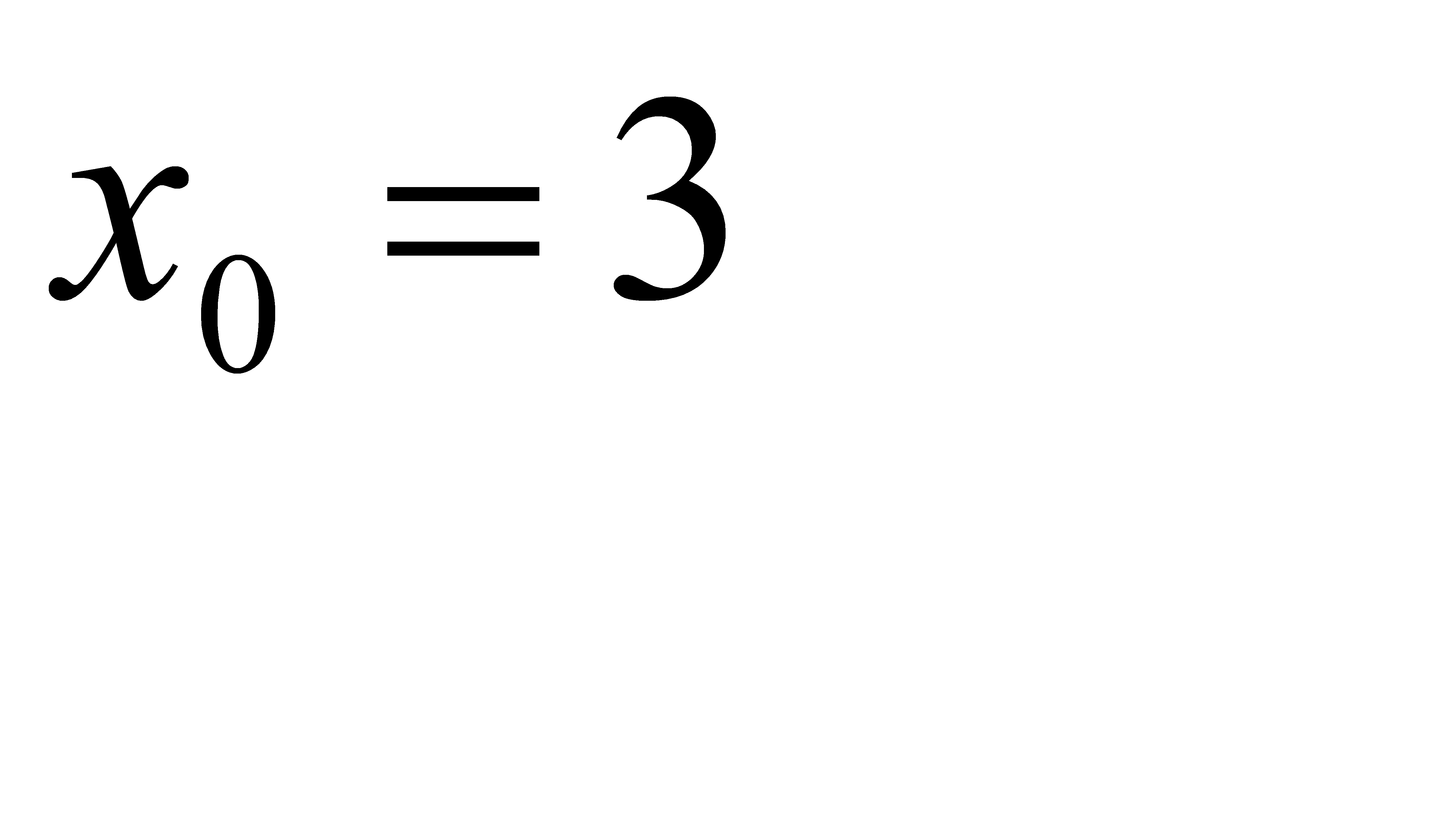 , c)
, c) 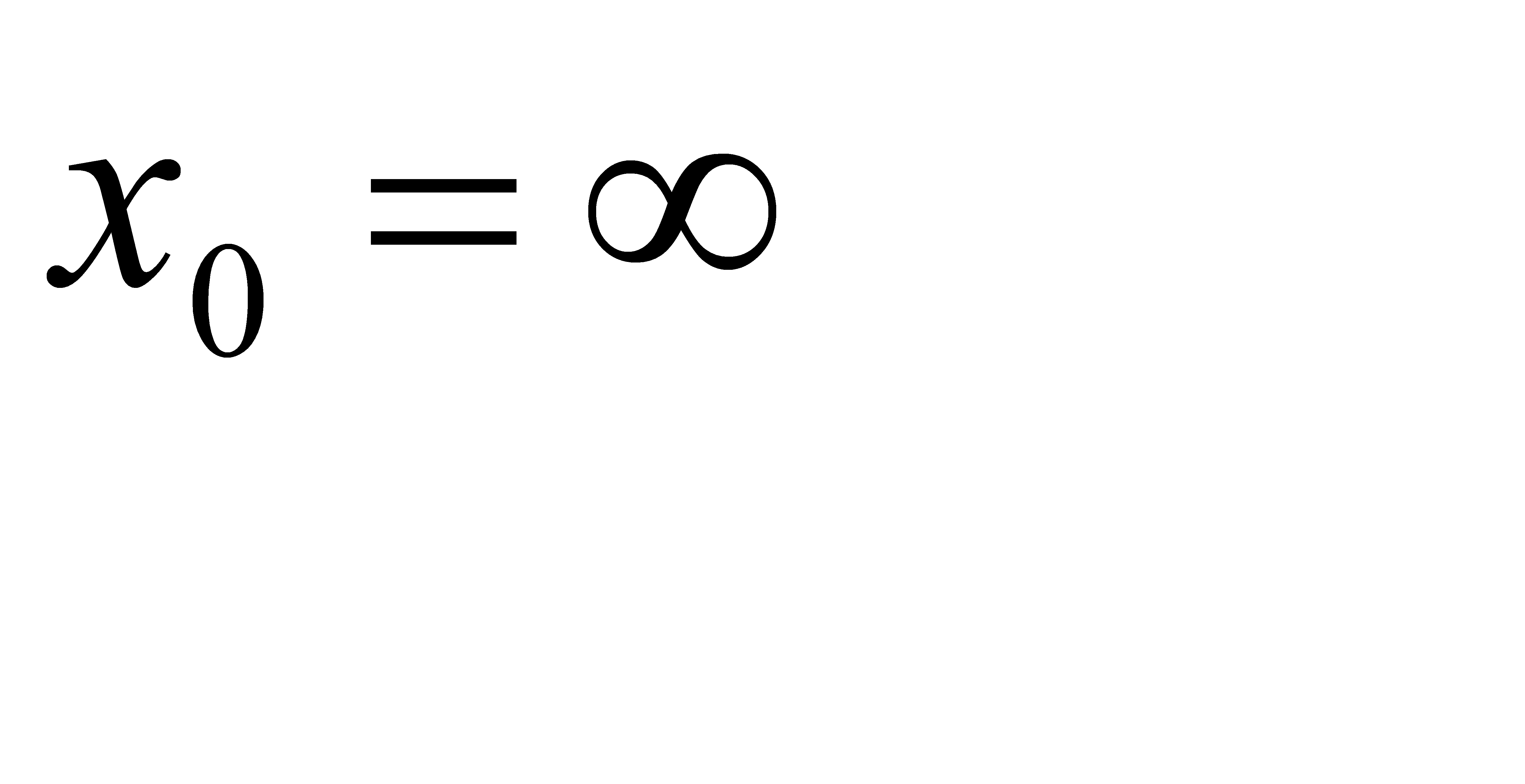 ;
;
2) 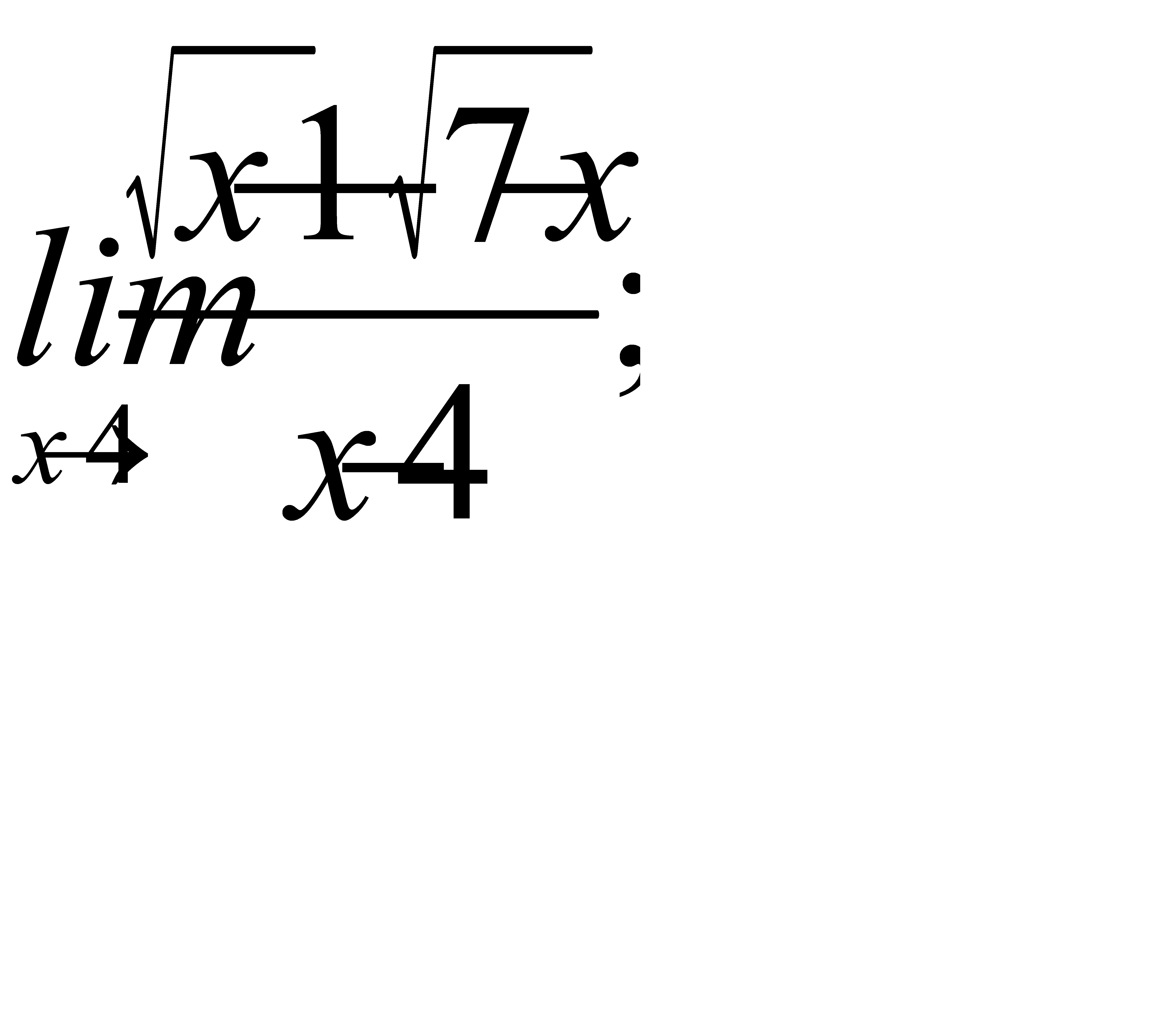 3)
3) 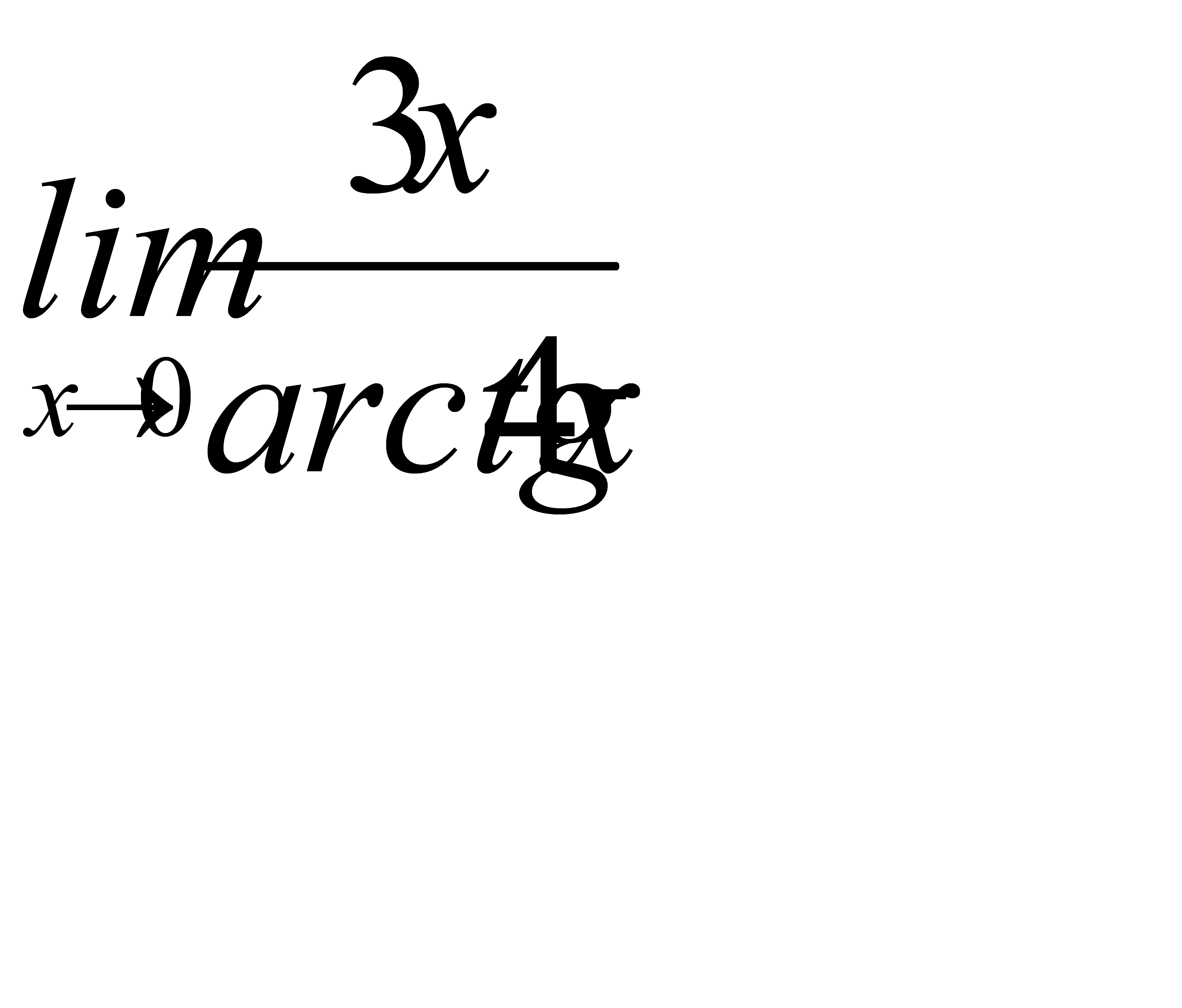 ;
;
4) 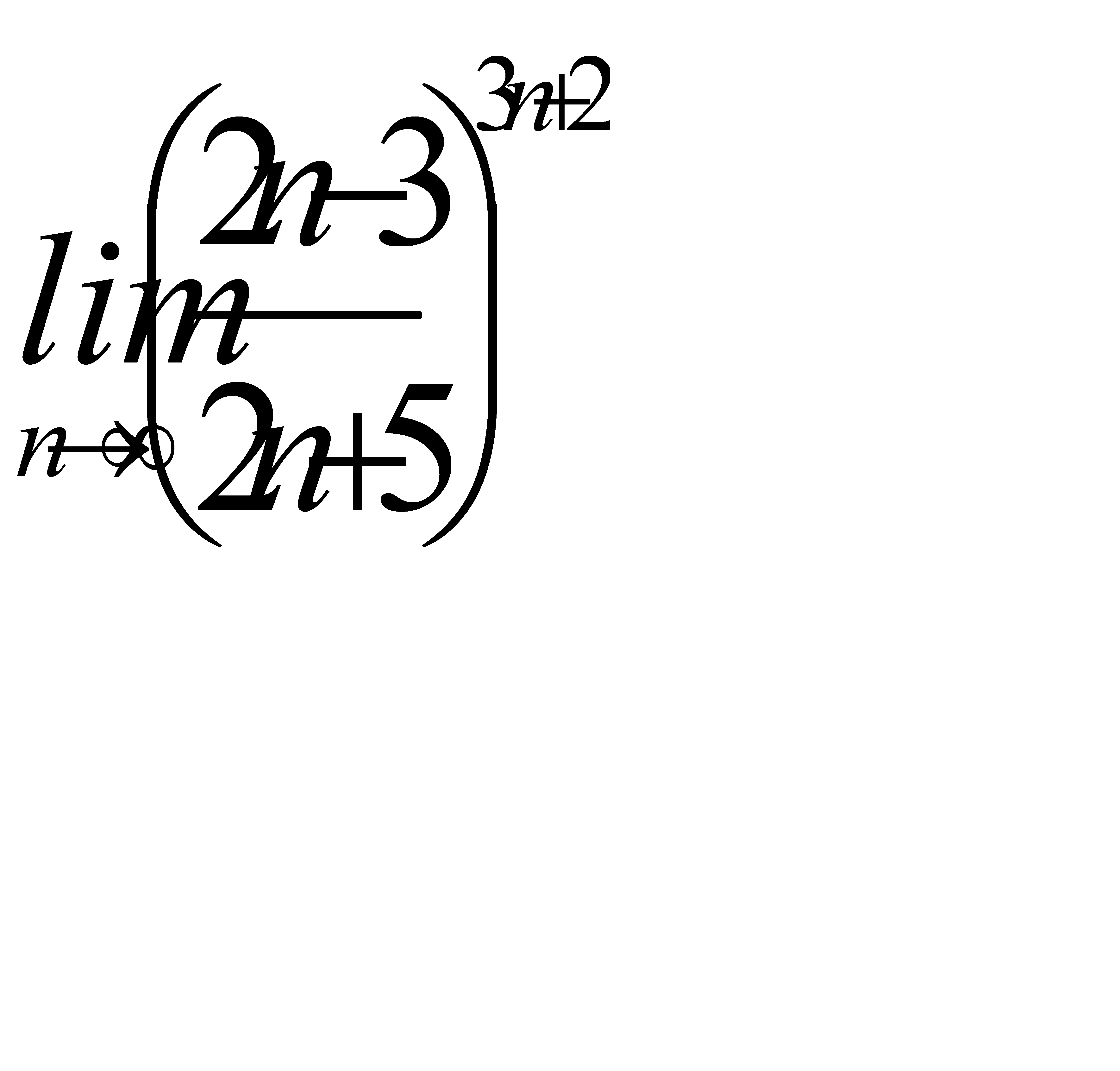
2. 1) 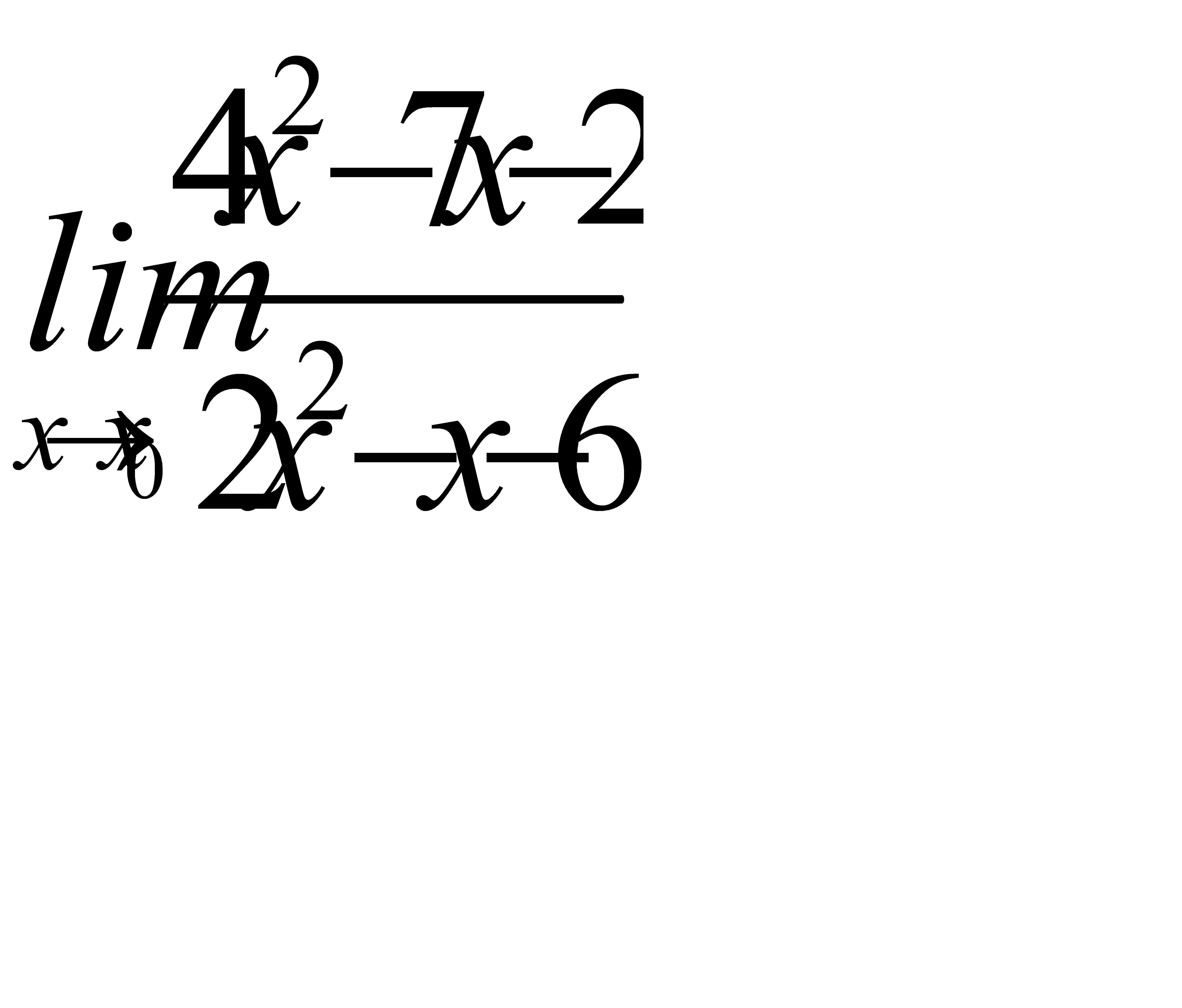 при a)
при a) 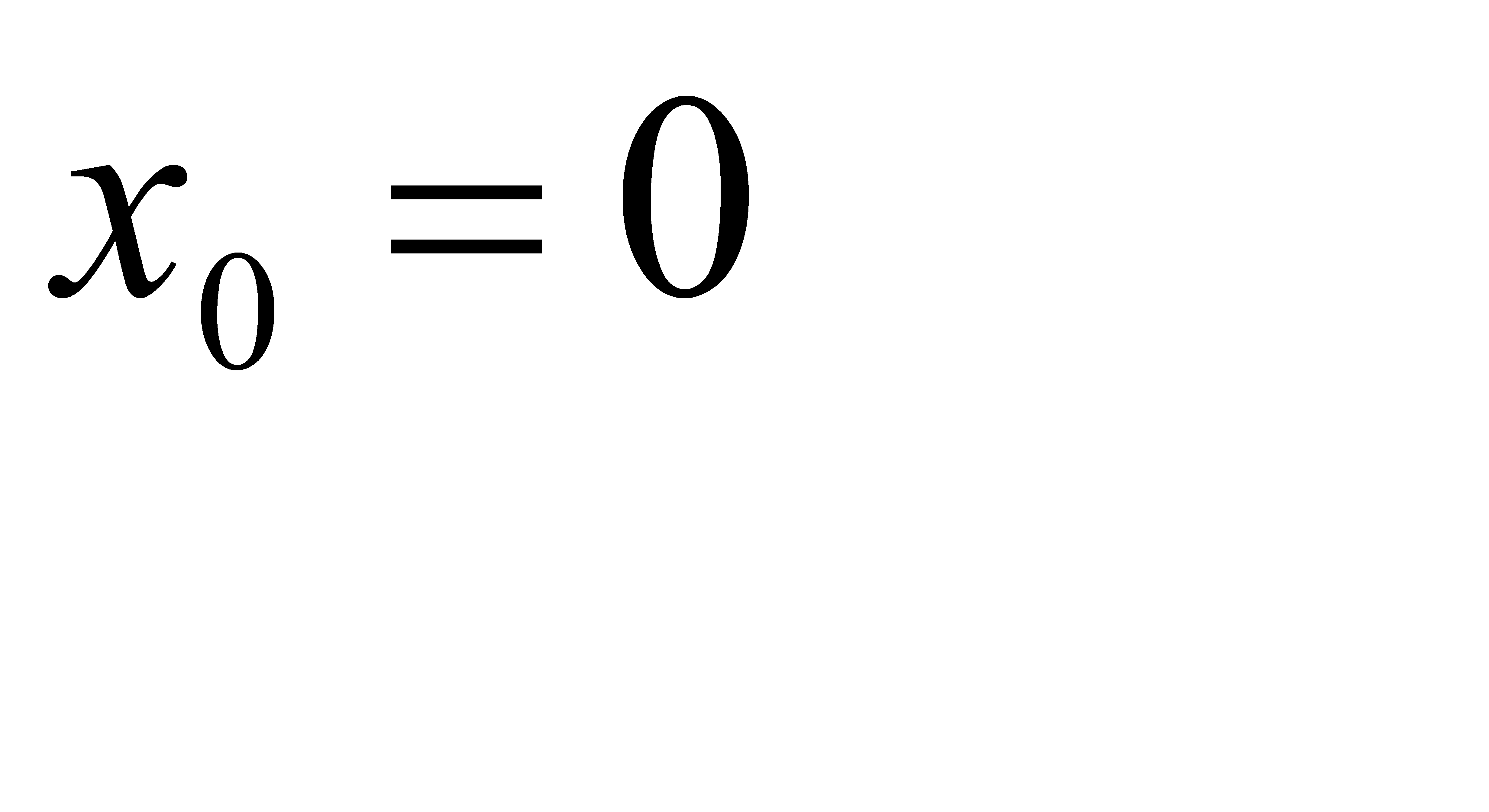 , b)
, b) 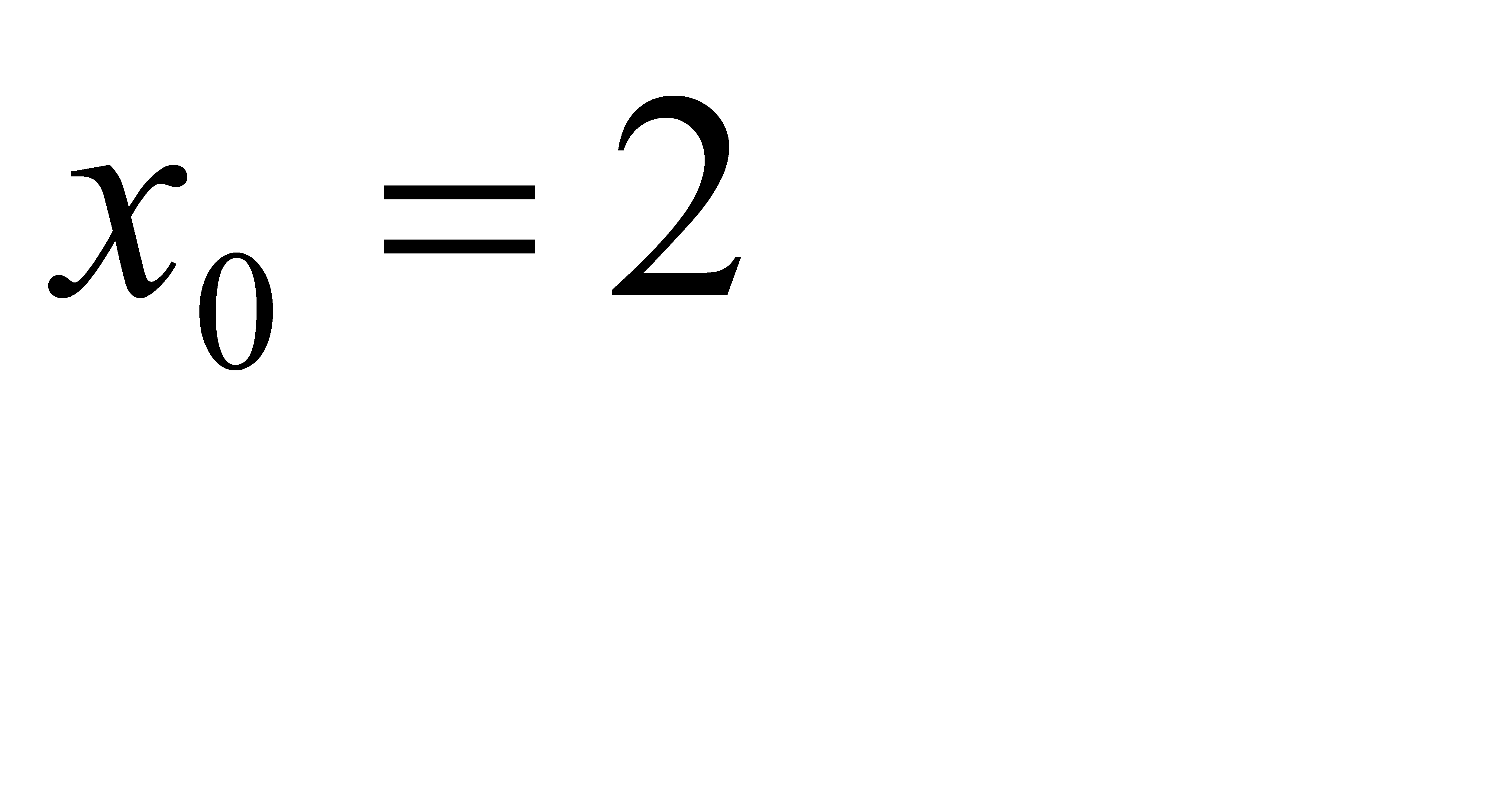 , c)
, c) 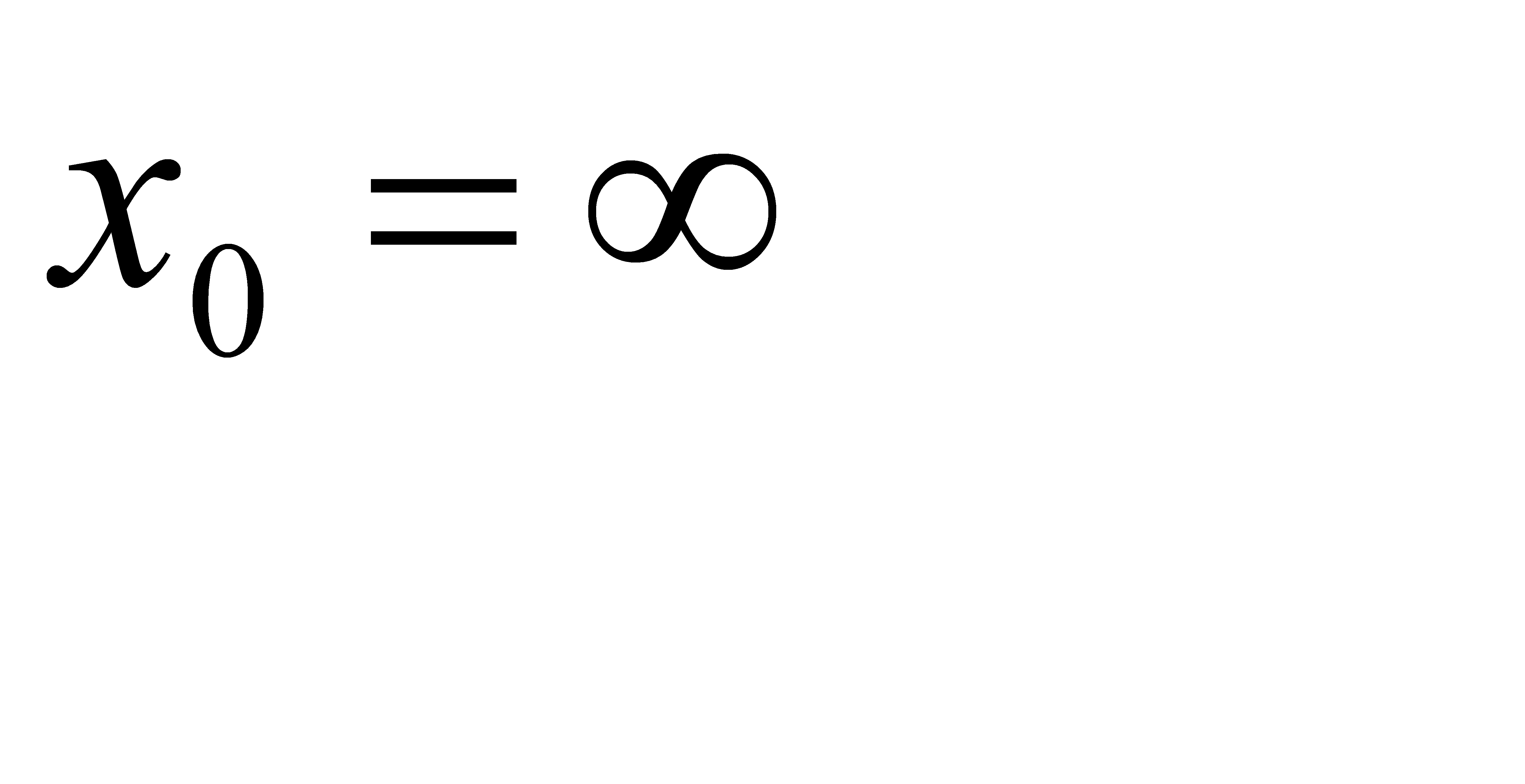 ;
;
2) 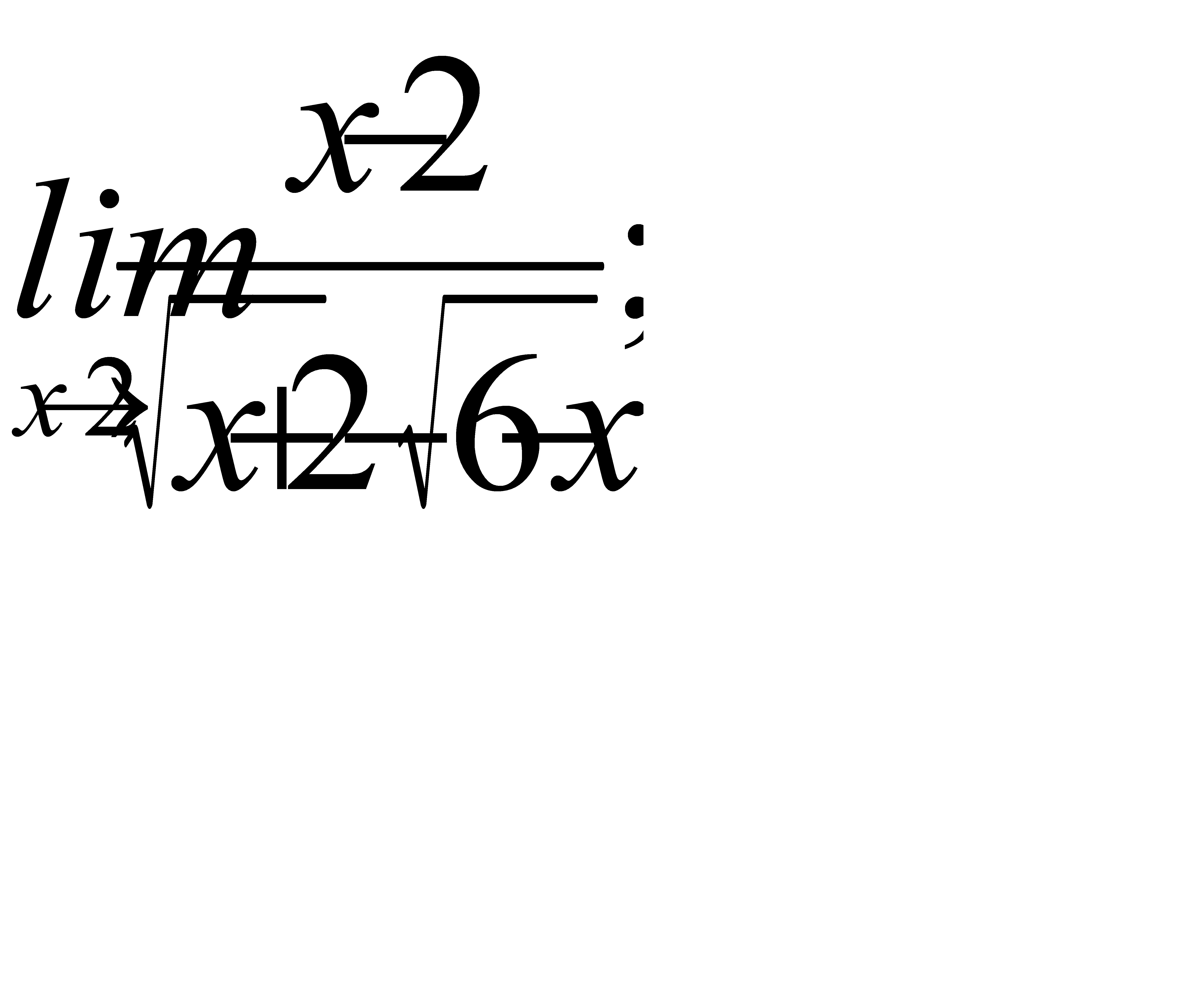 3)
3) 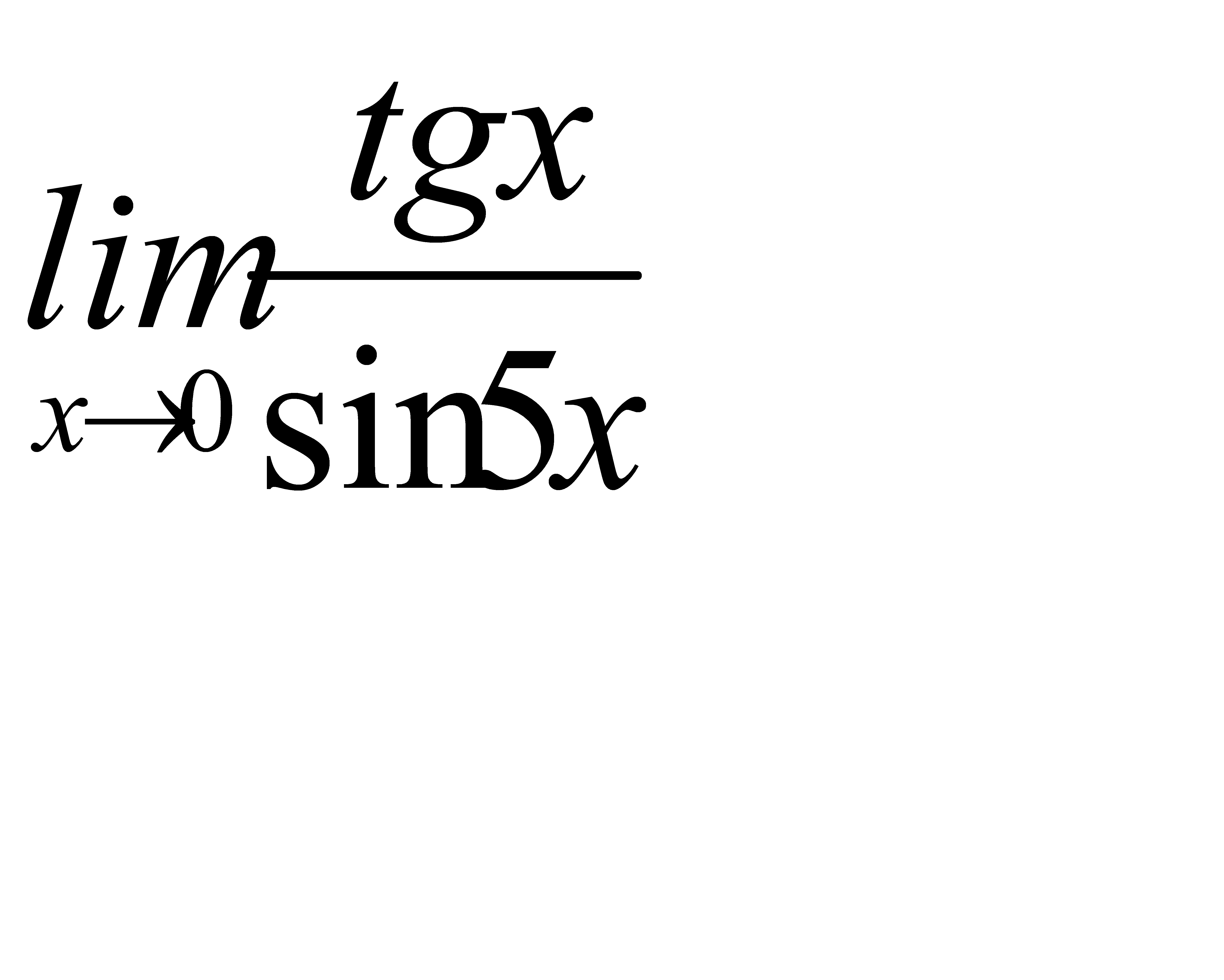 ;
;
4) 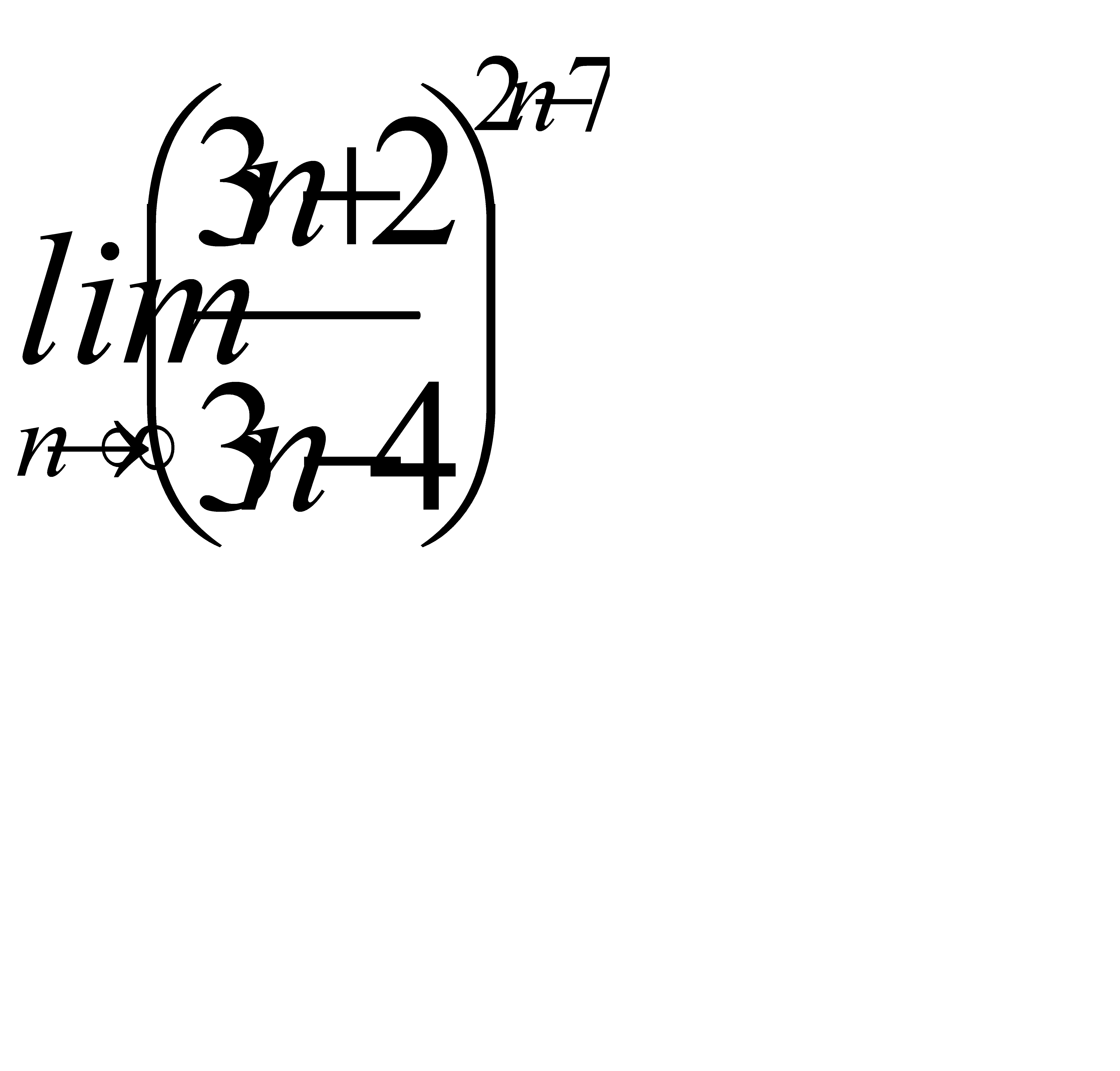
3. 1) 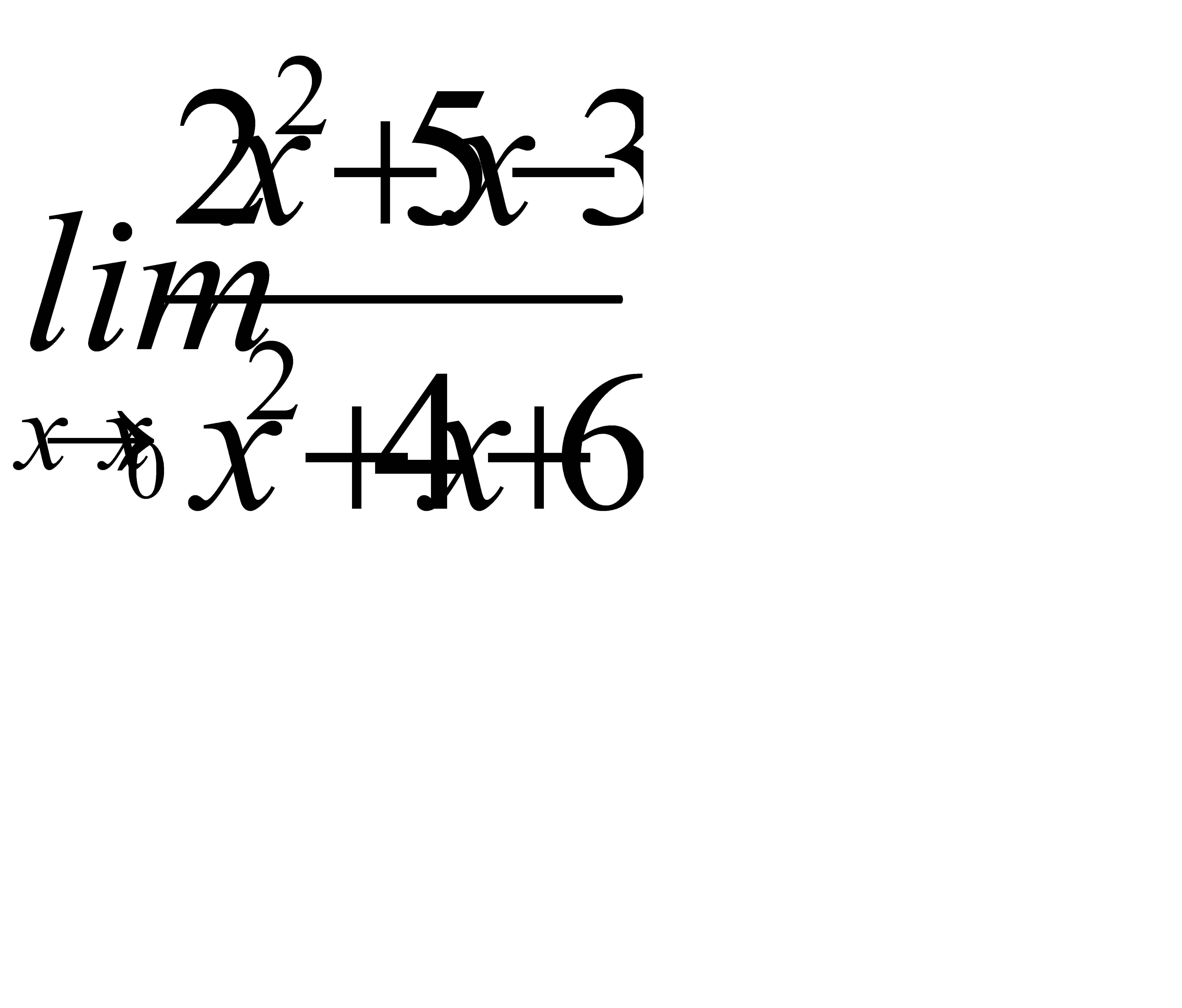 при a)
при a) 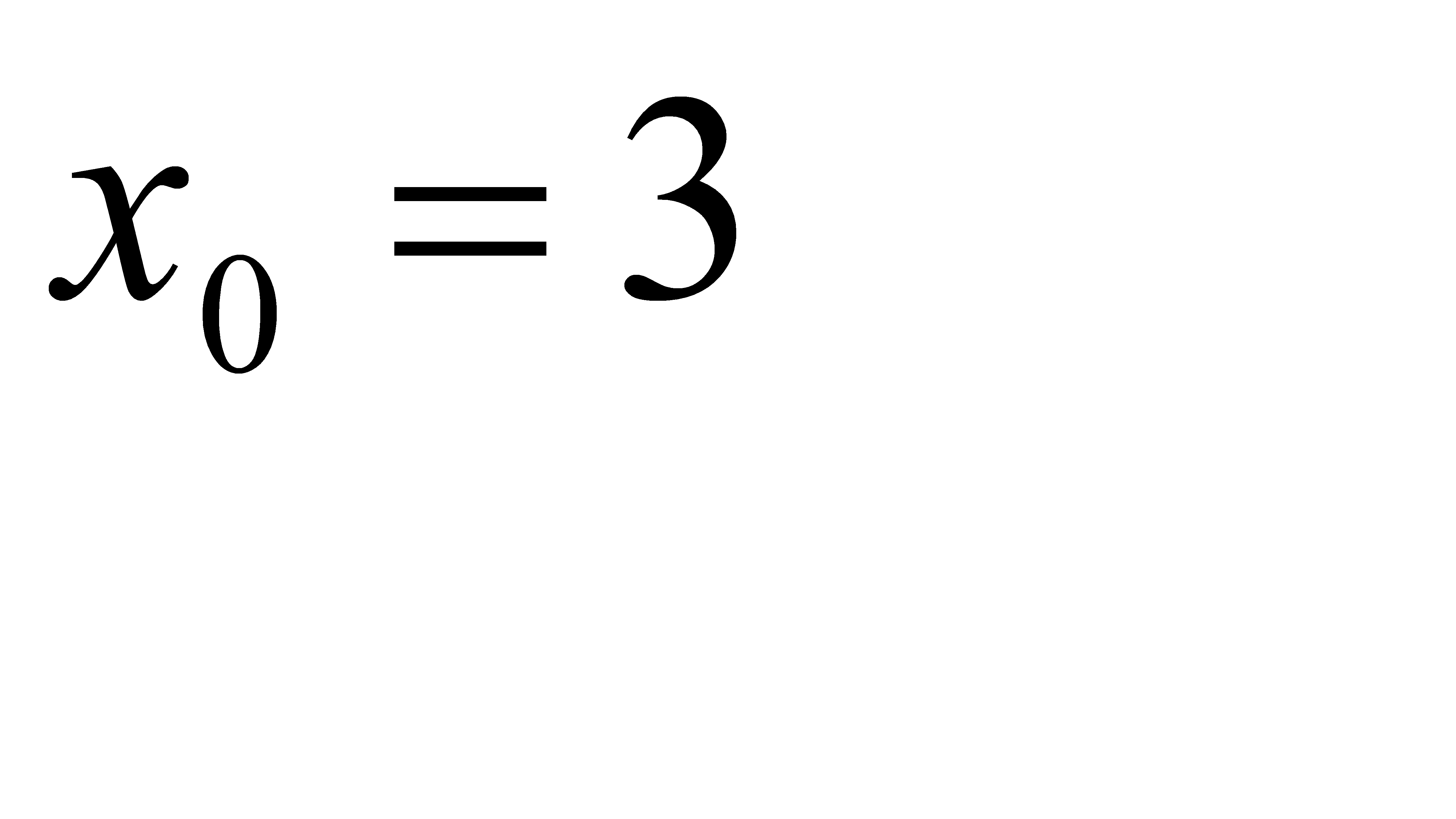 , b)
, b) 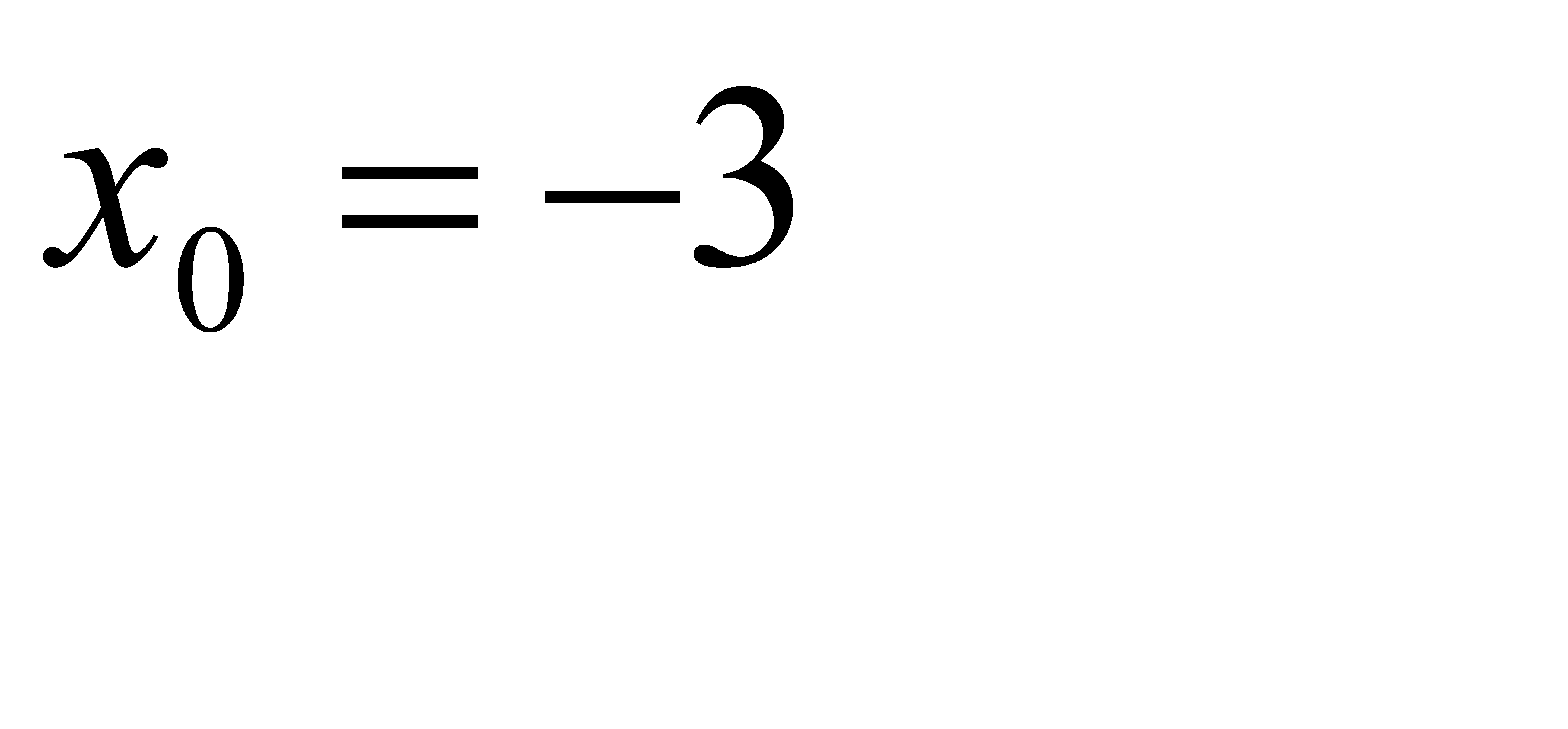 , c)
, c) 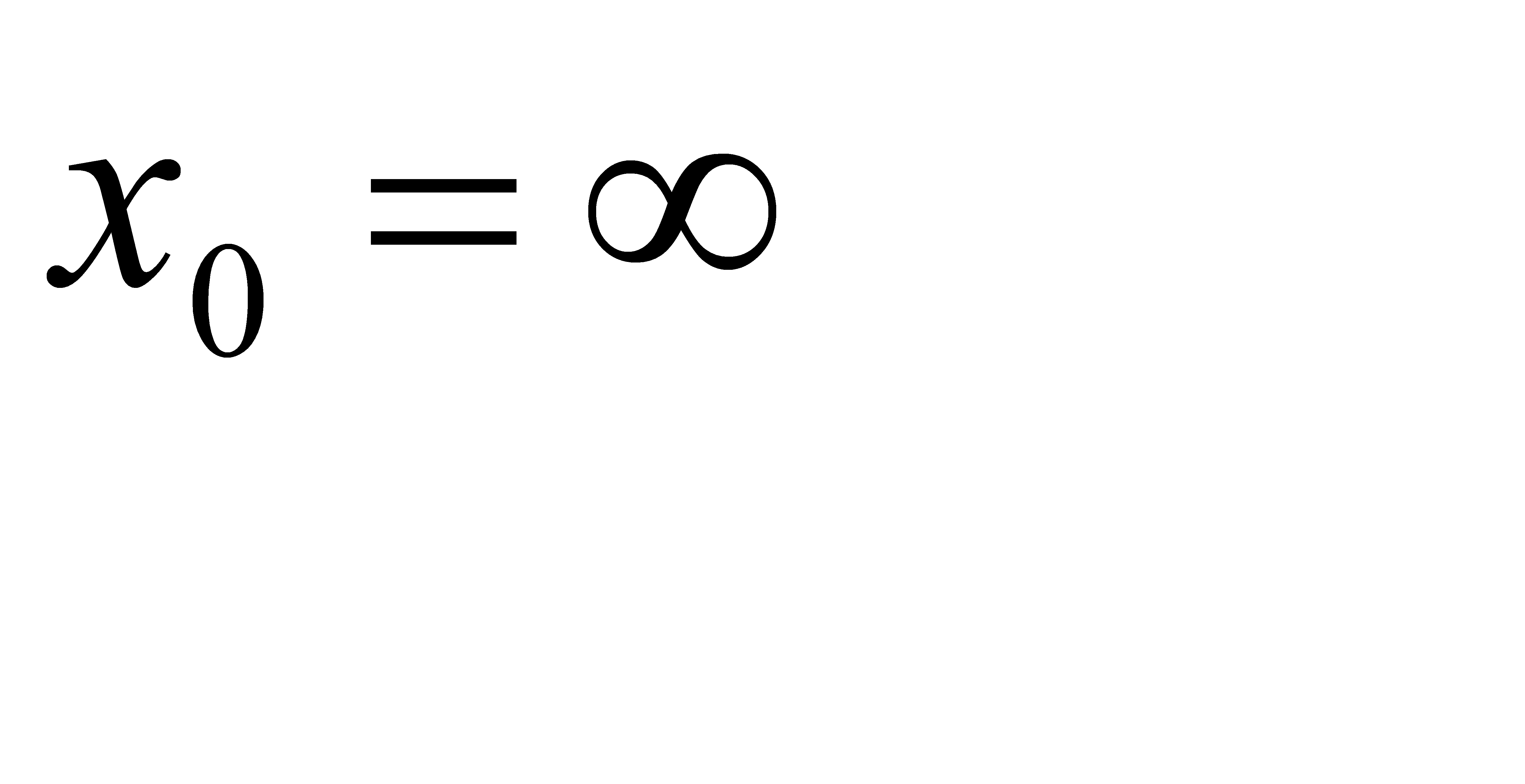 ;
;
2) 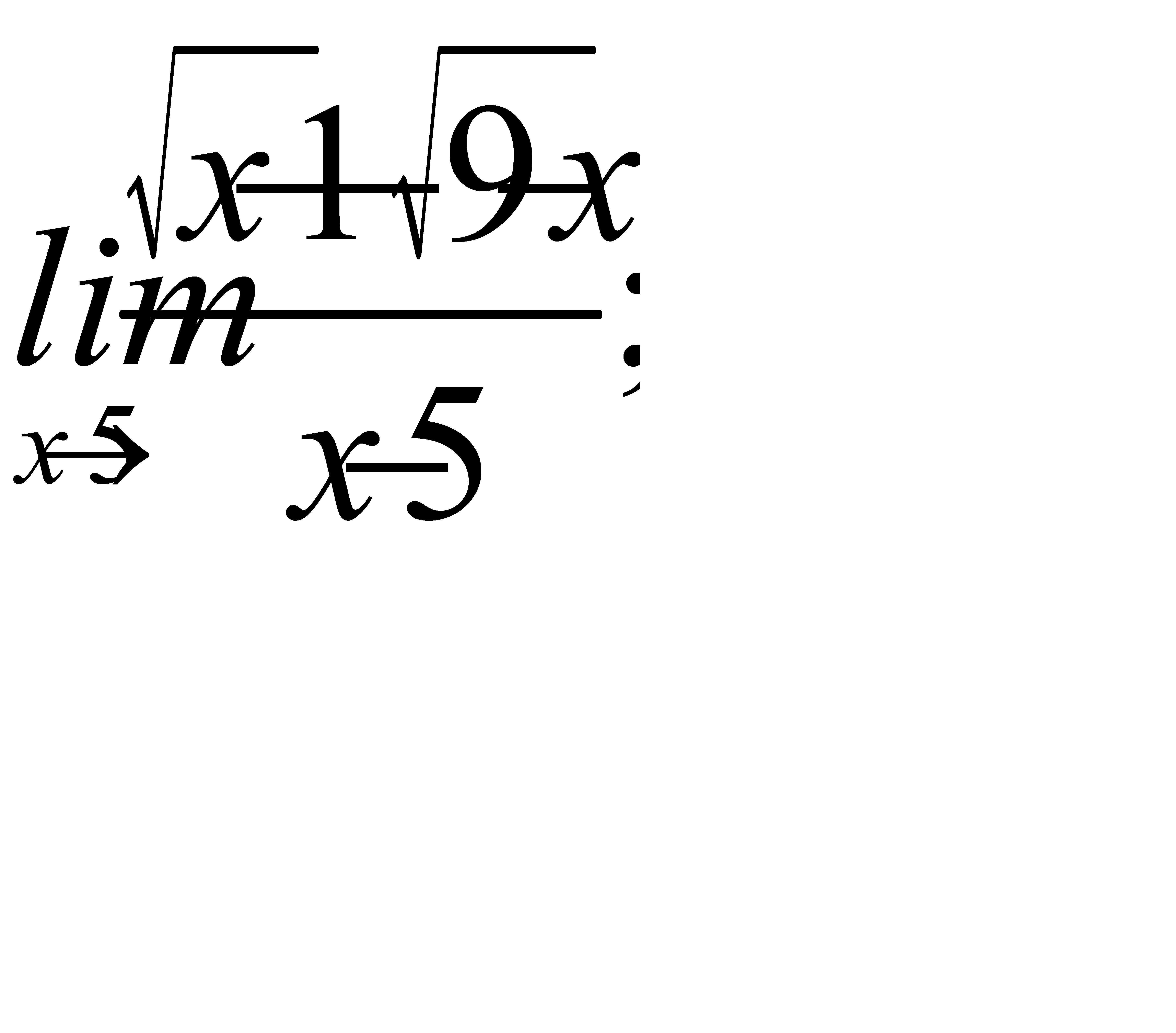 3)
3) 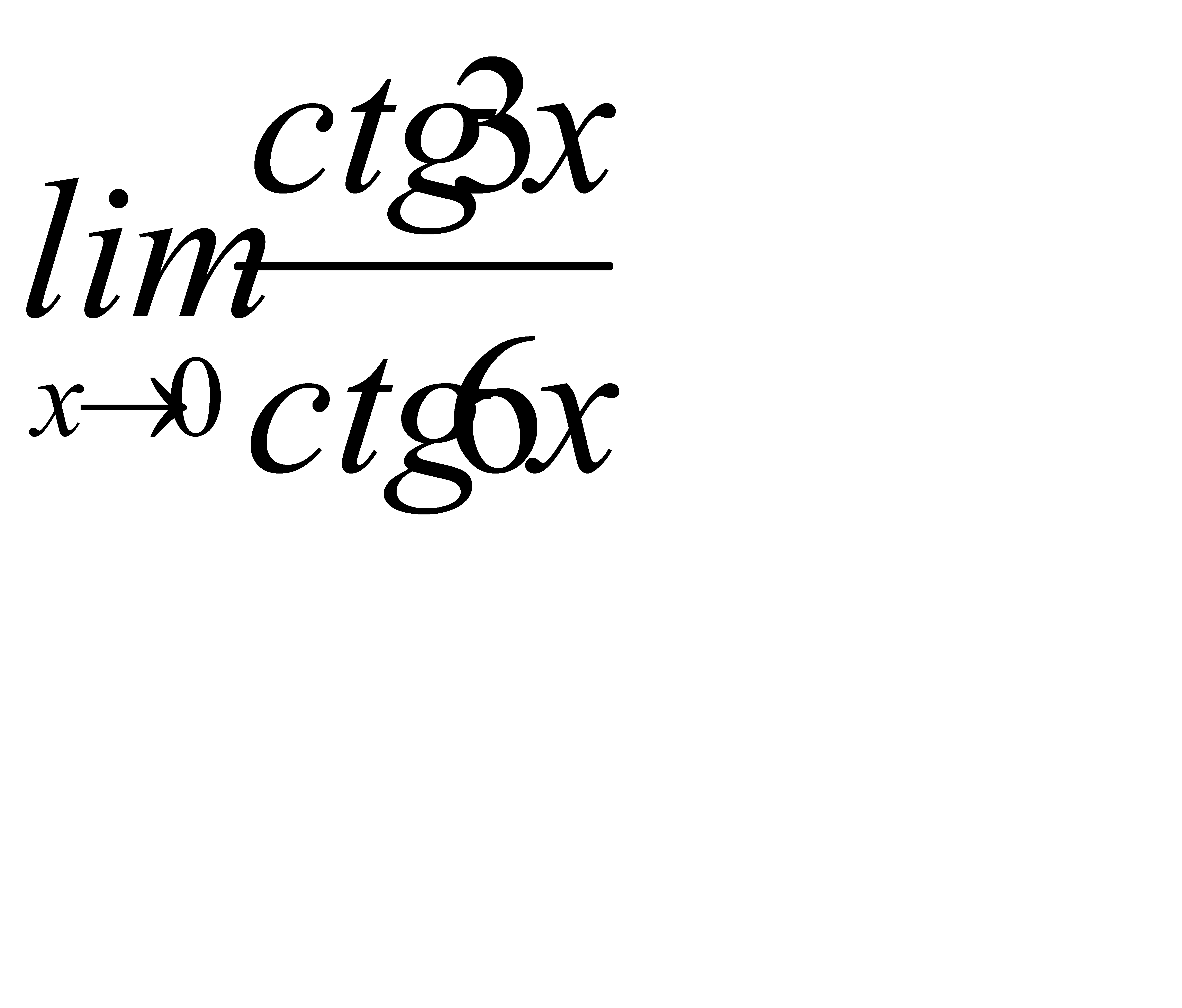 ;
;
4) 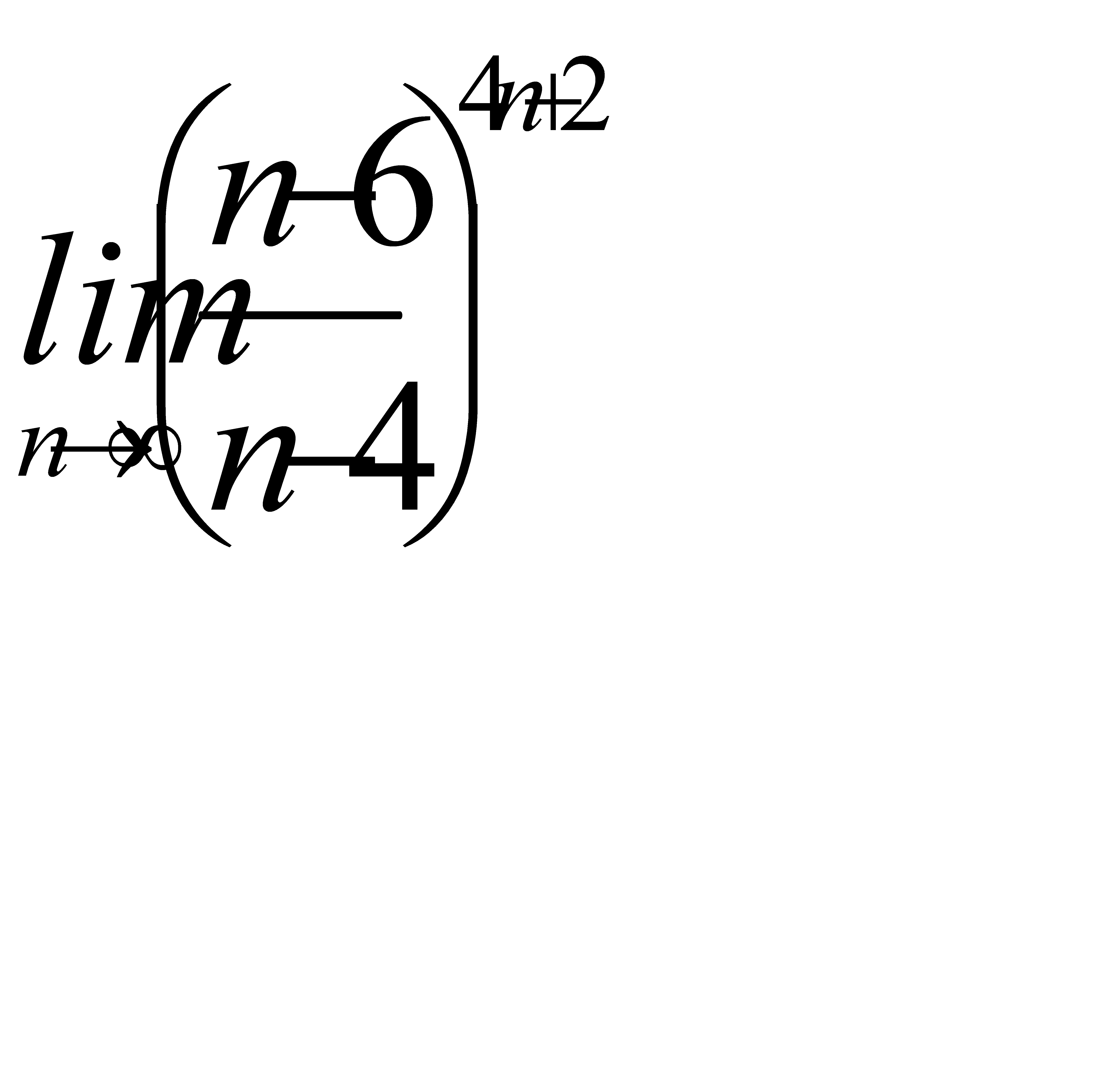
4. 1) 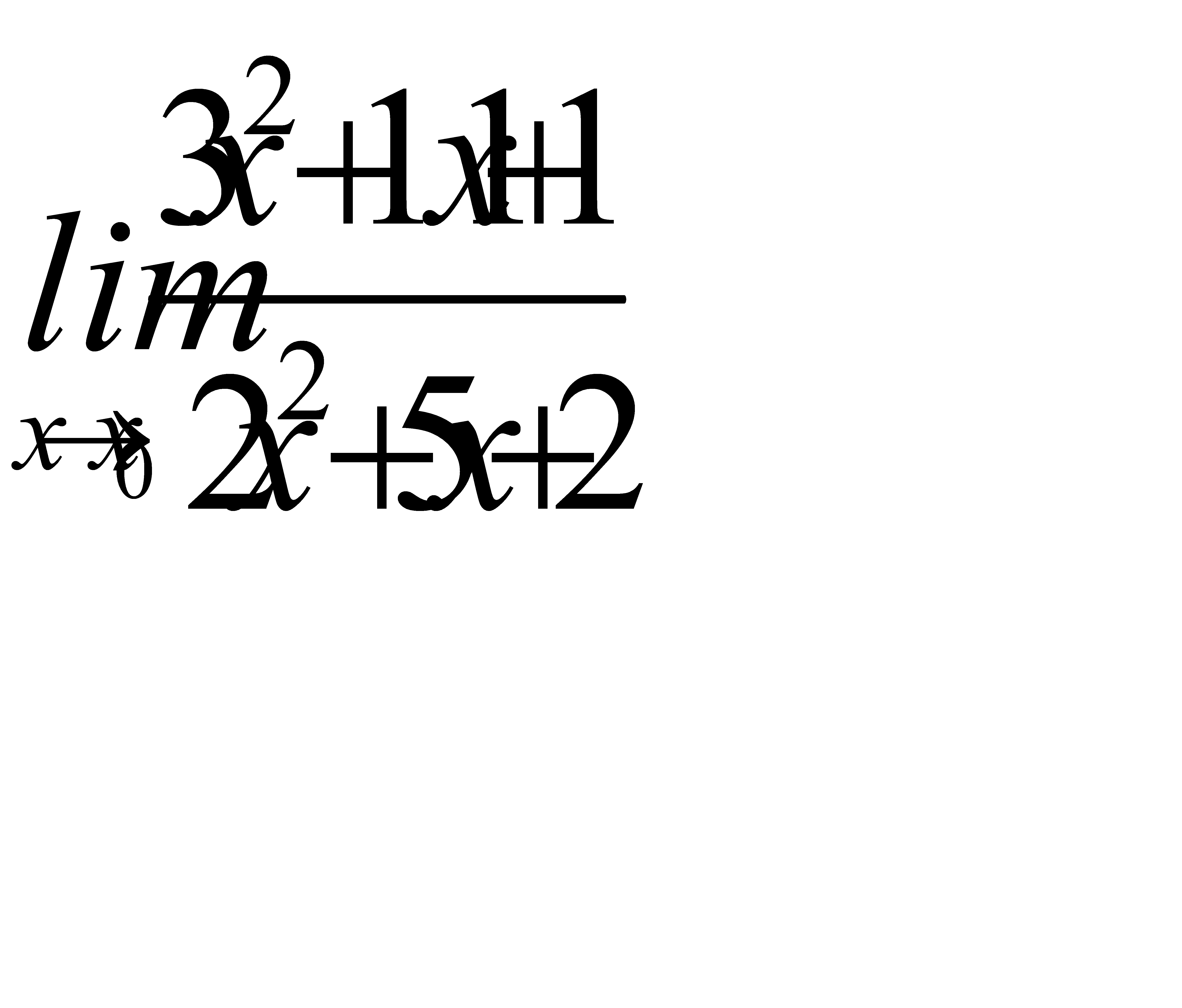 при a)
при a) 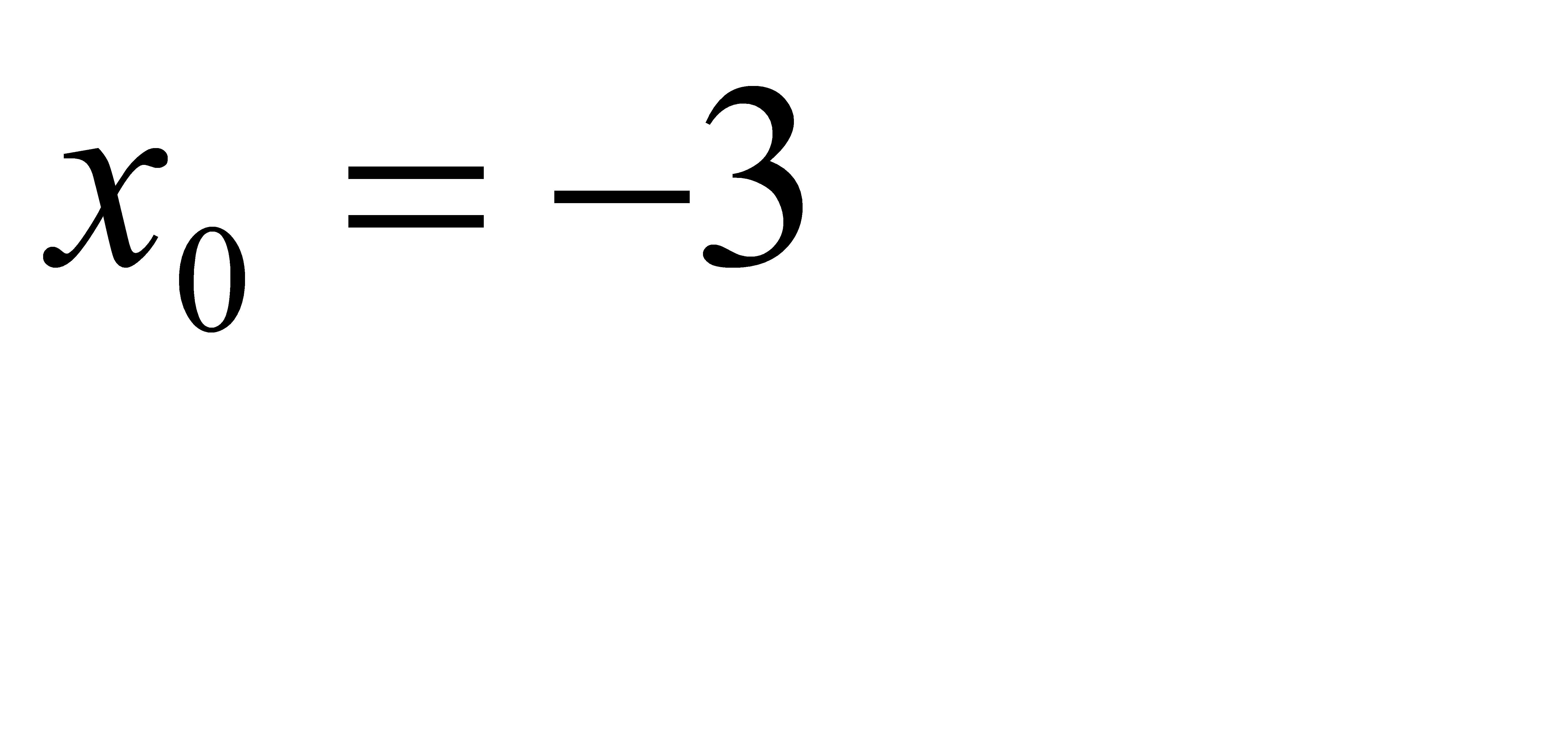 , b)
, b) 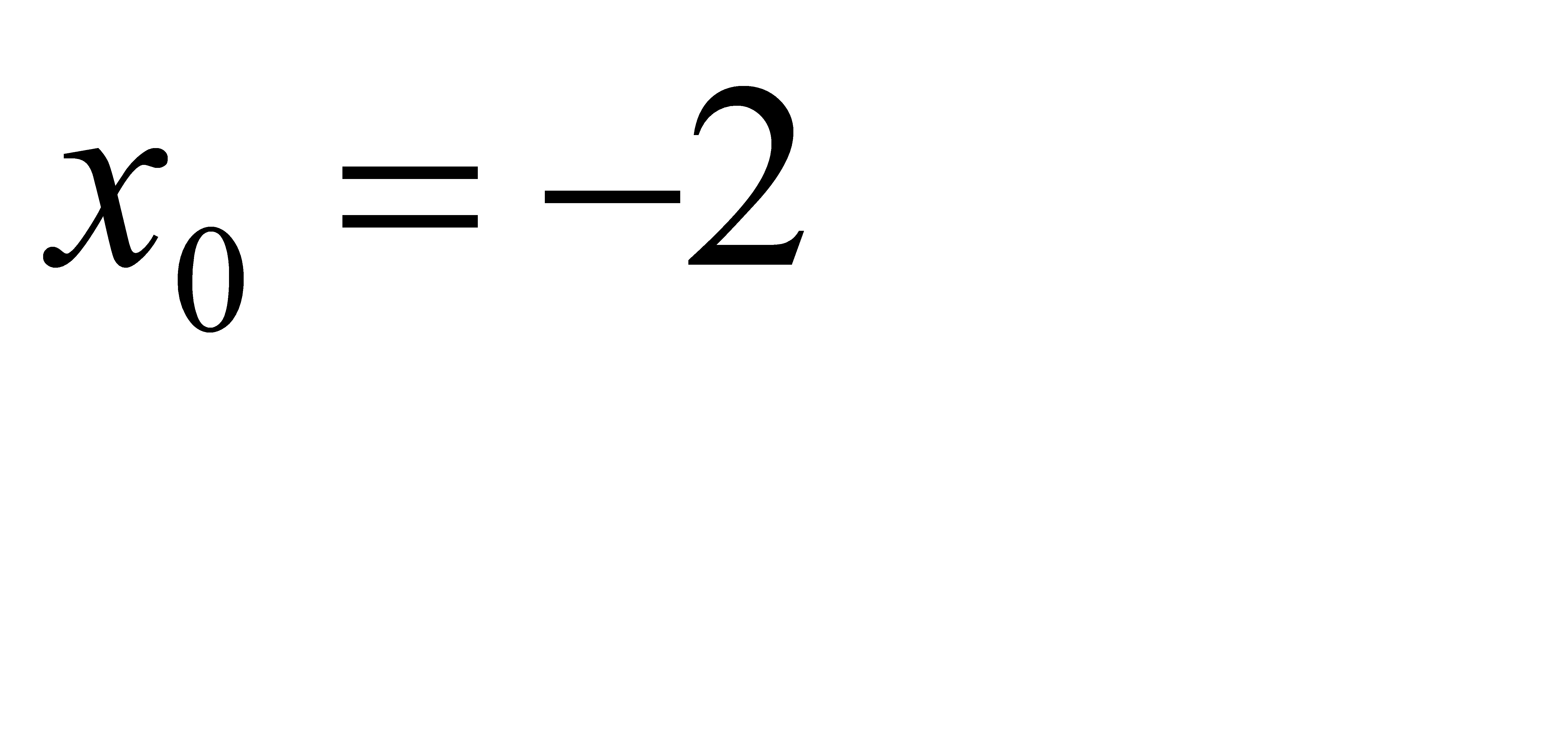 , c)
, c) 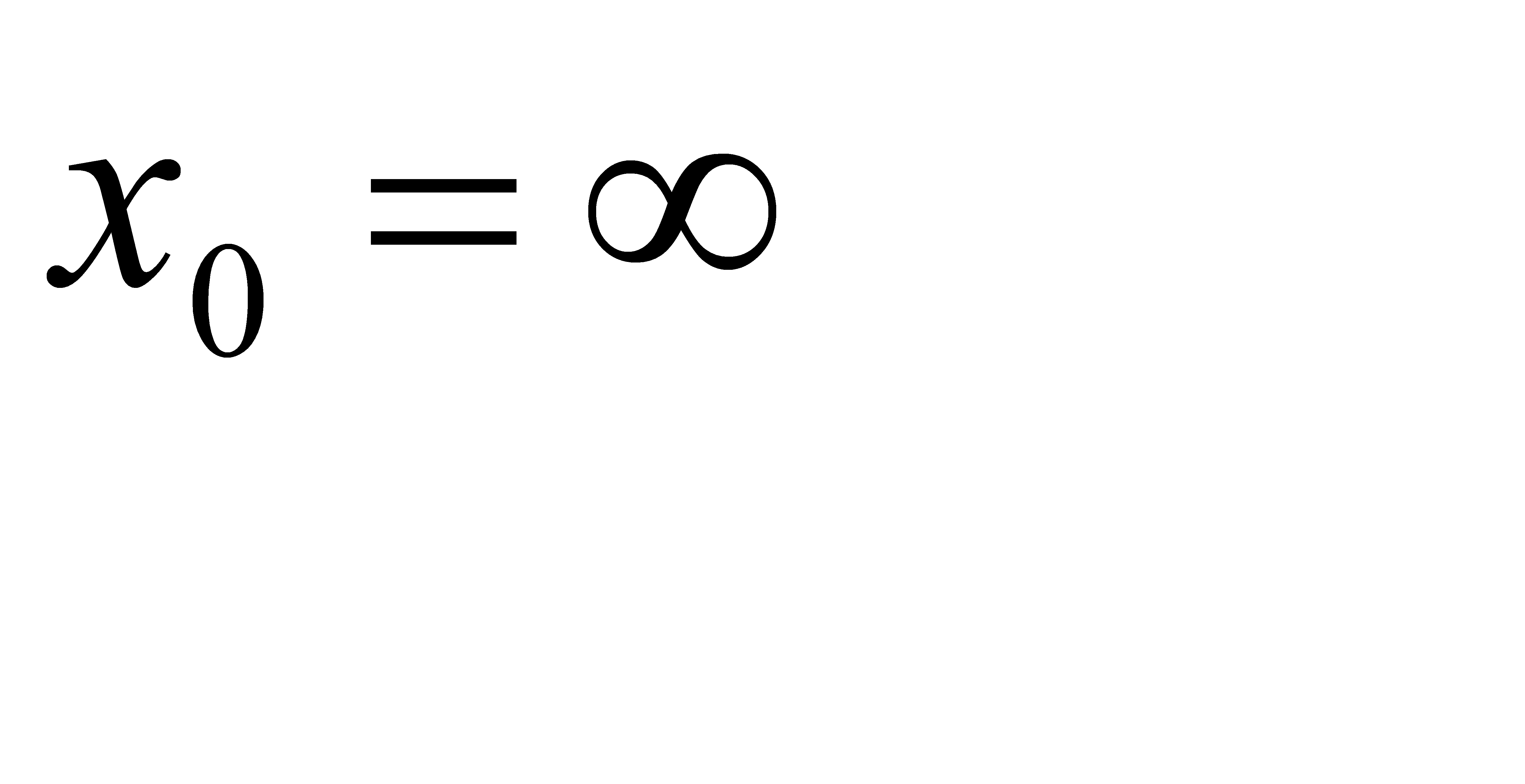 ;
;
2) 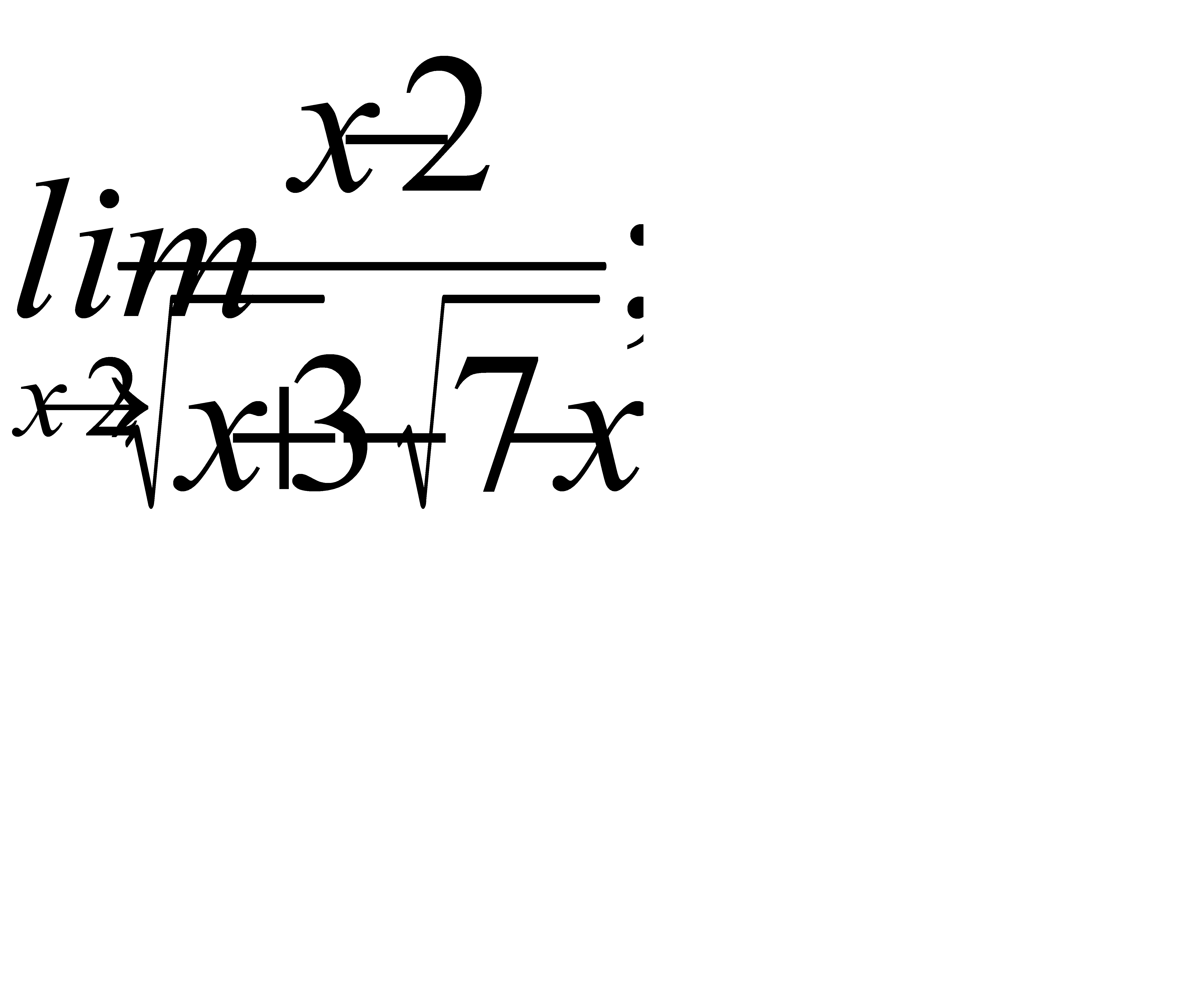 3)
3) 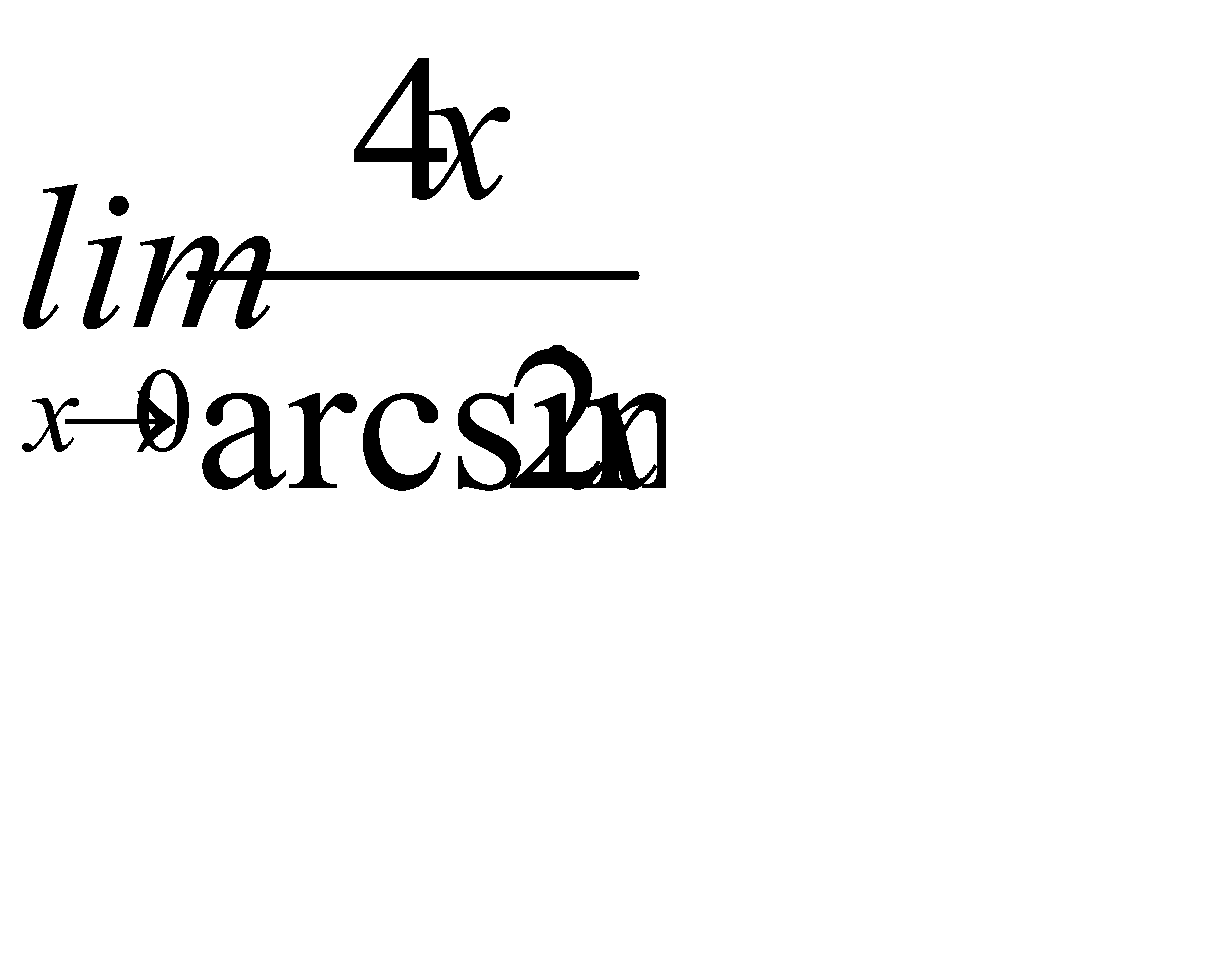 ;
;
4) 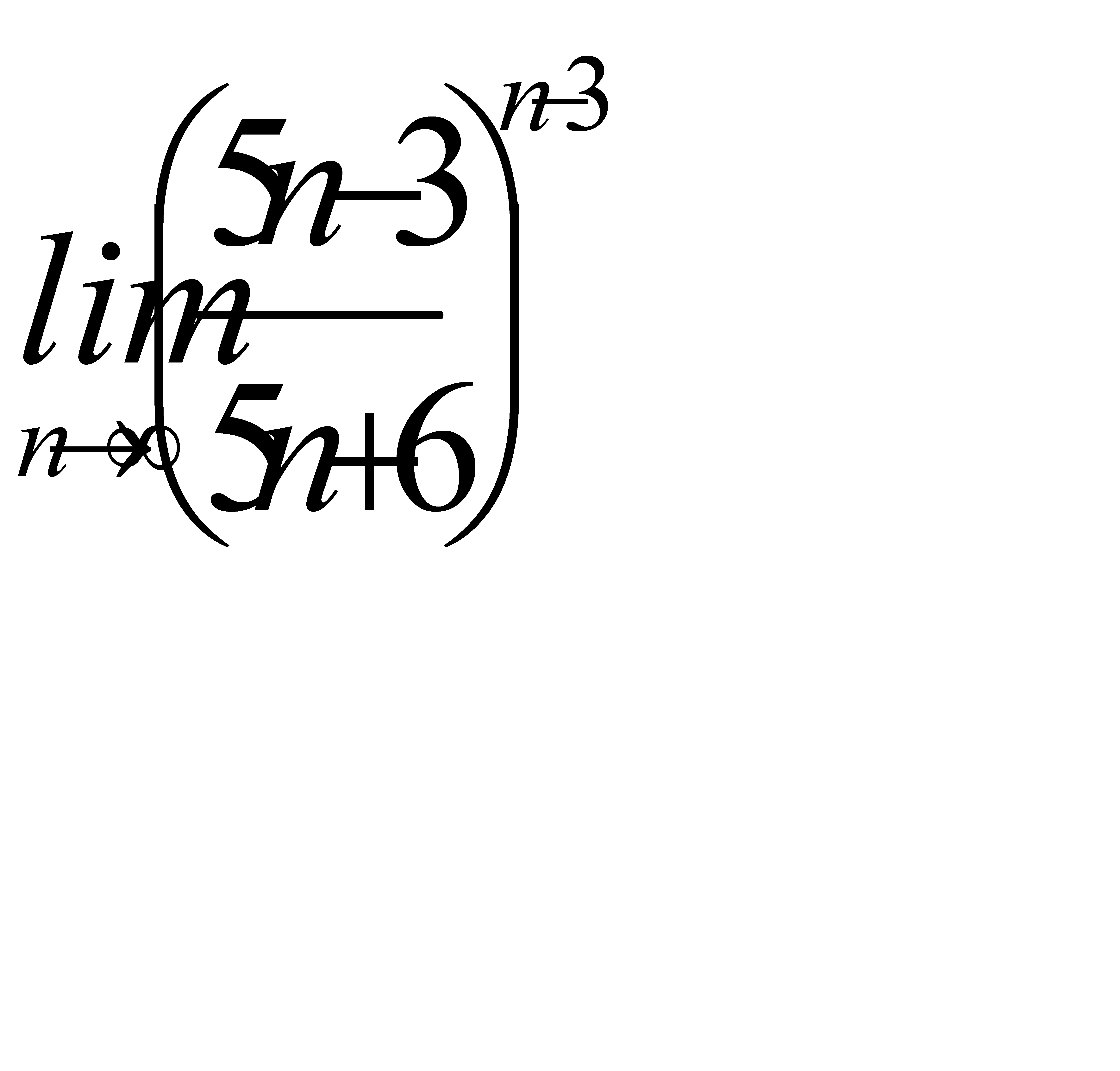
5. 1) 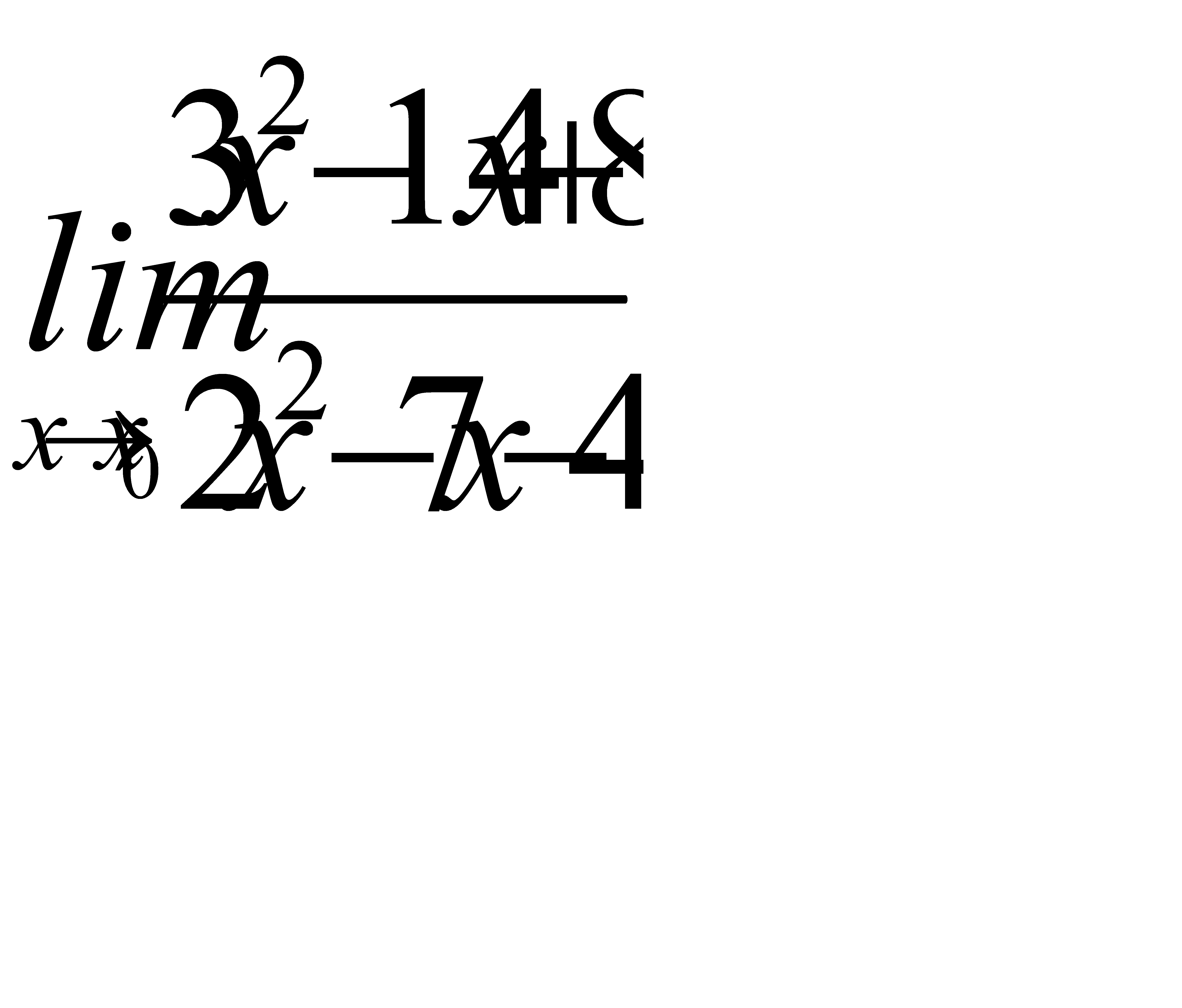 при a)
при a) 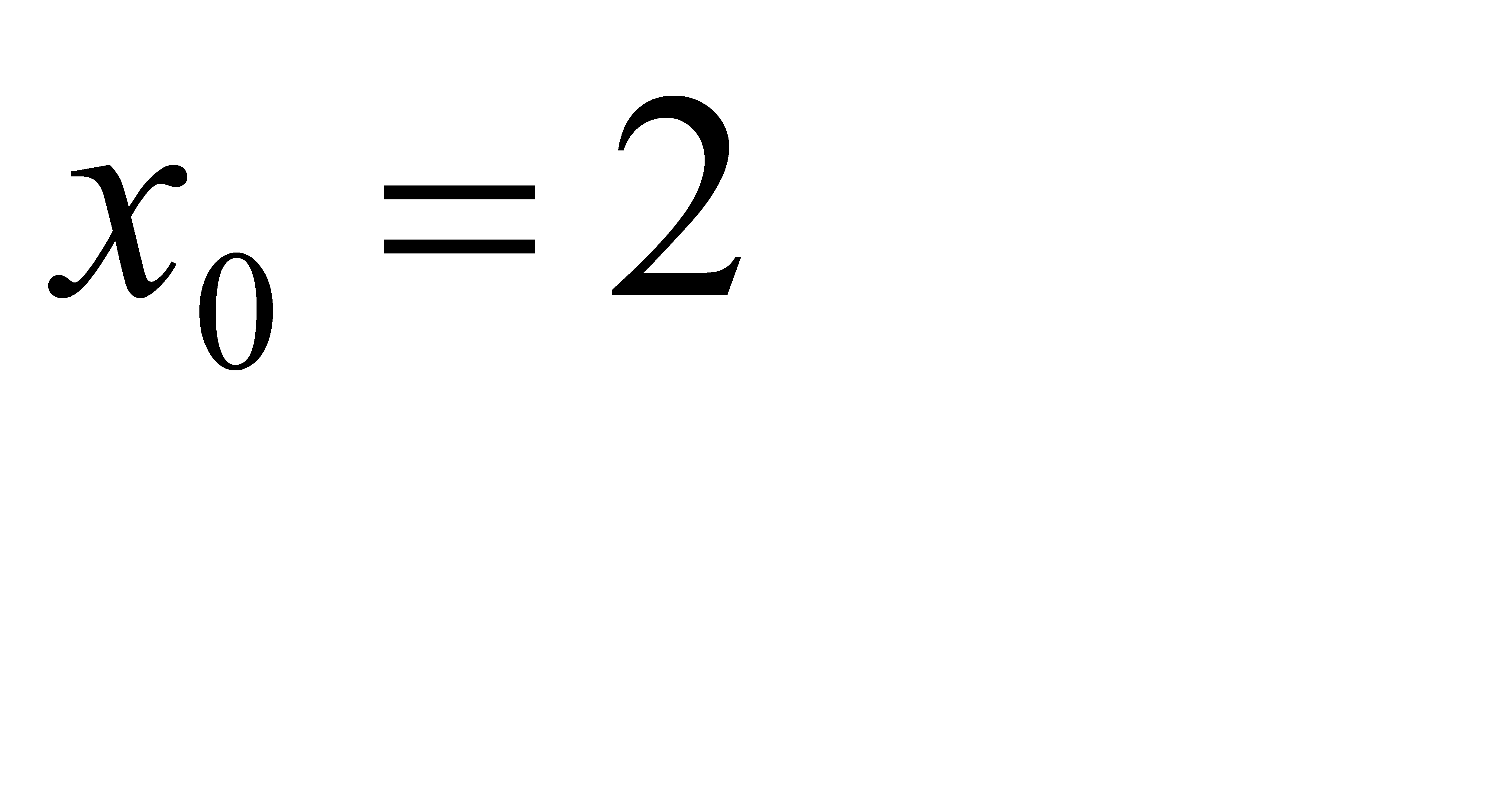 , b)
, b) 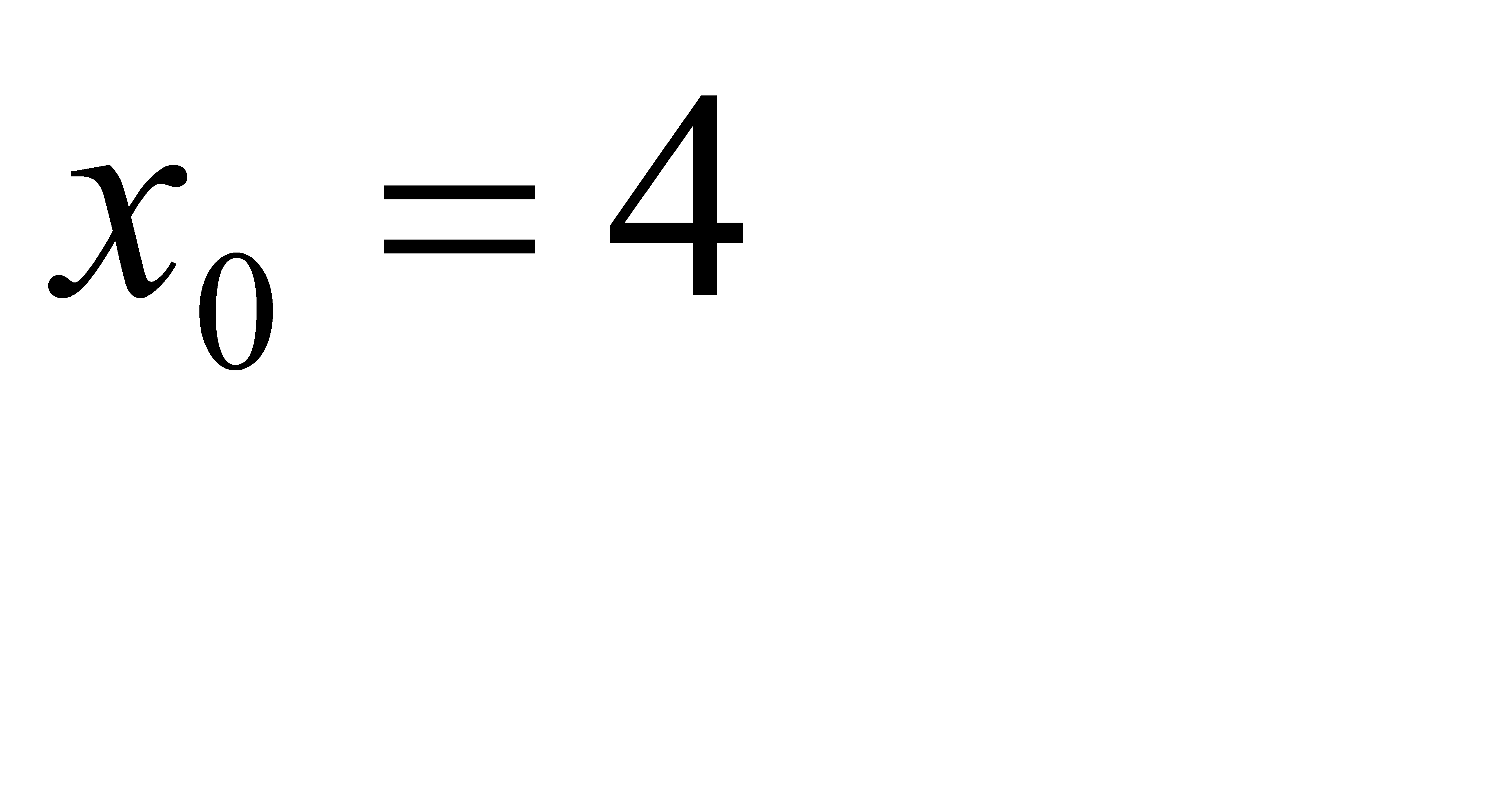 , c)
, c) 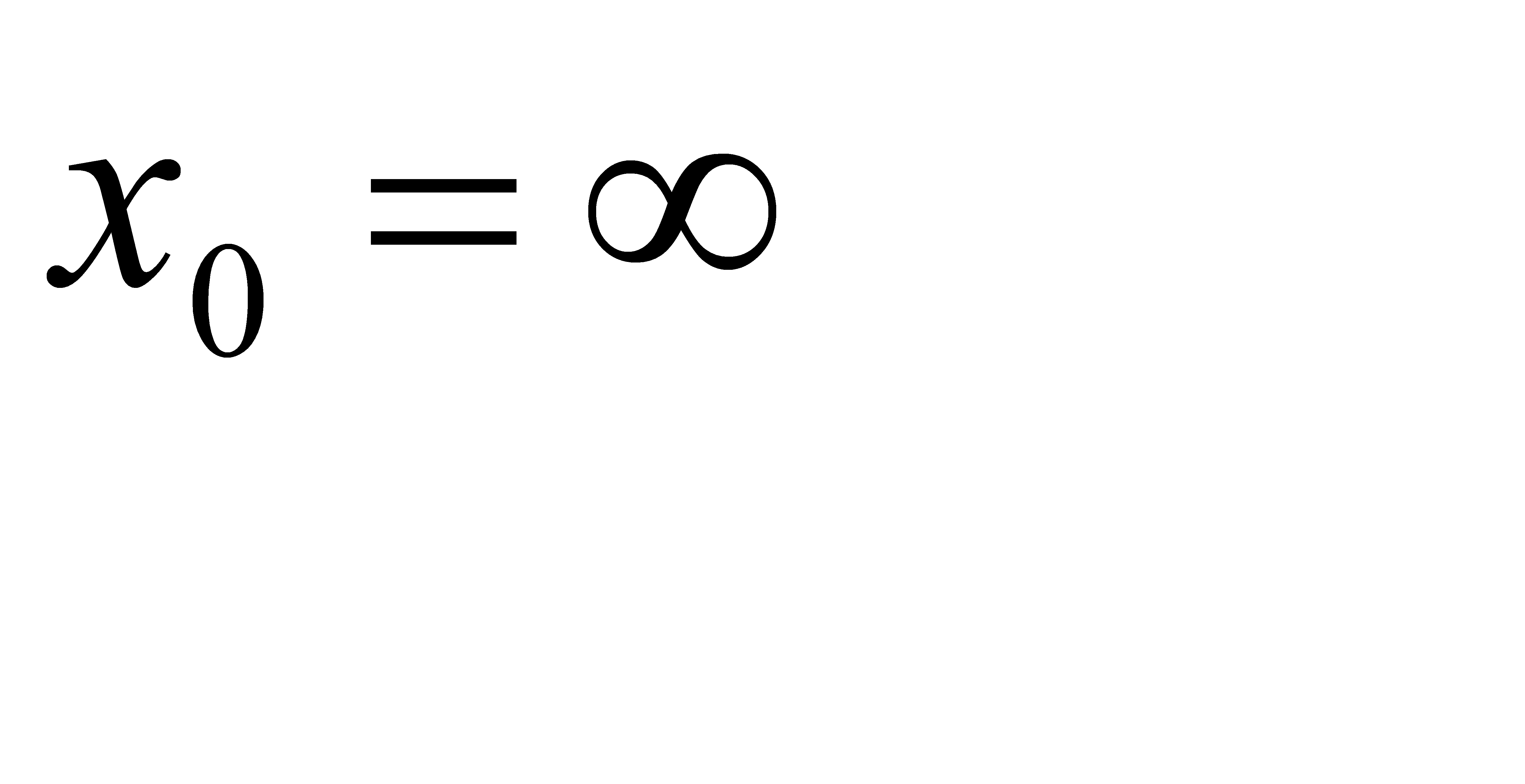 ;
;
2) 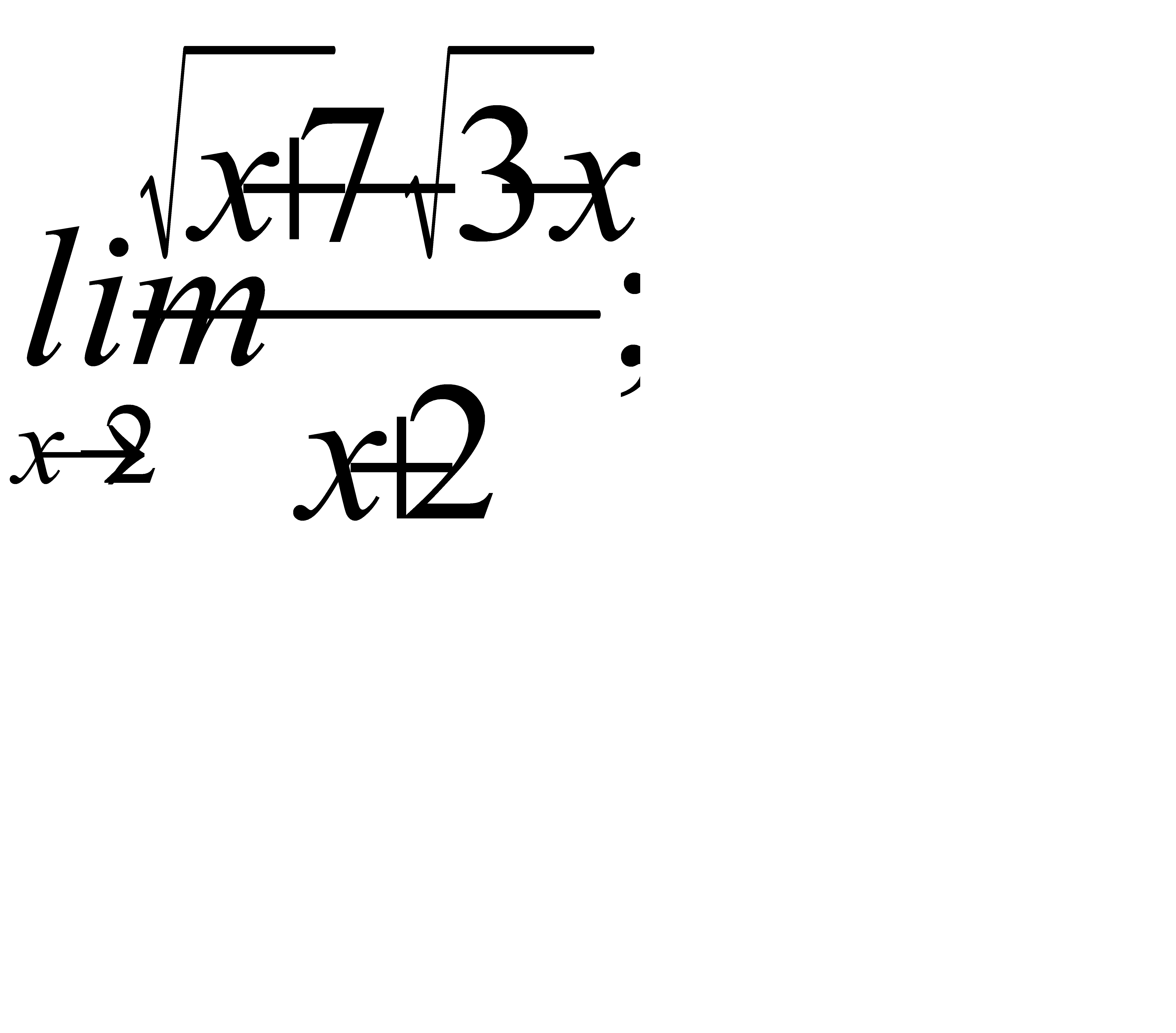 3)
3) 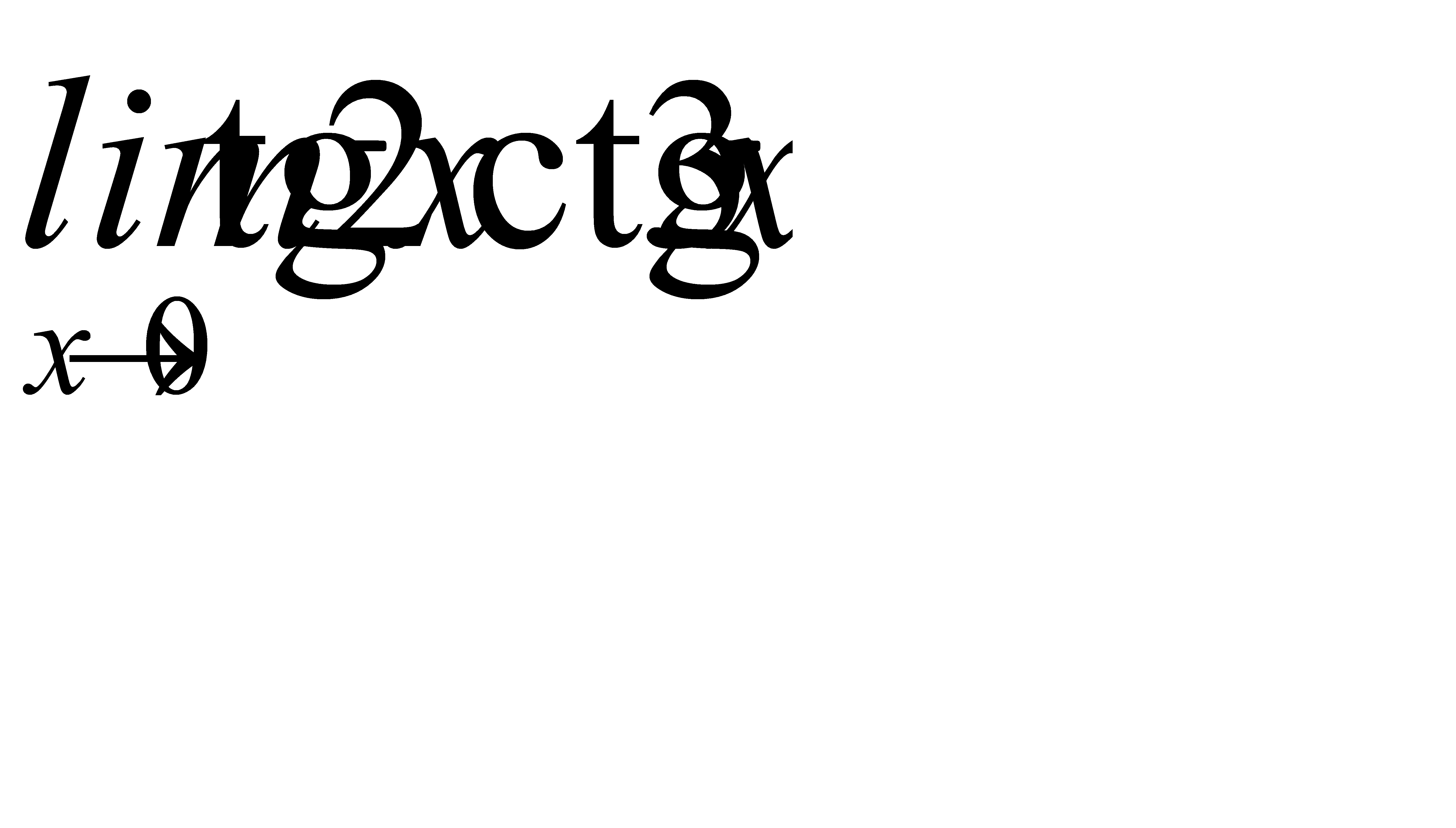 ;
;
4) 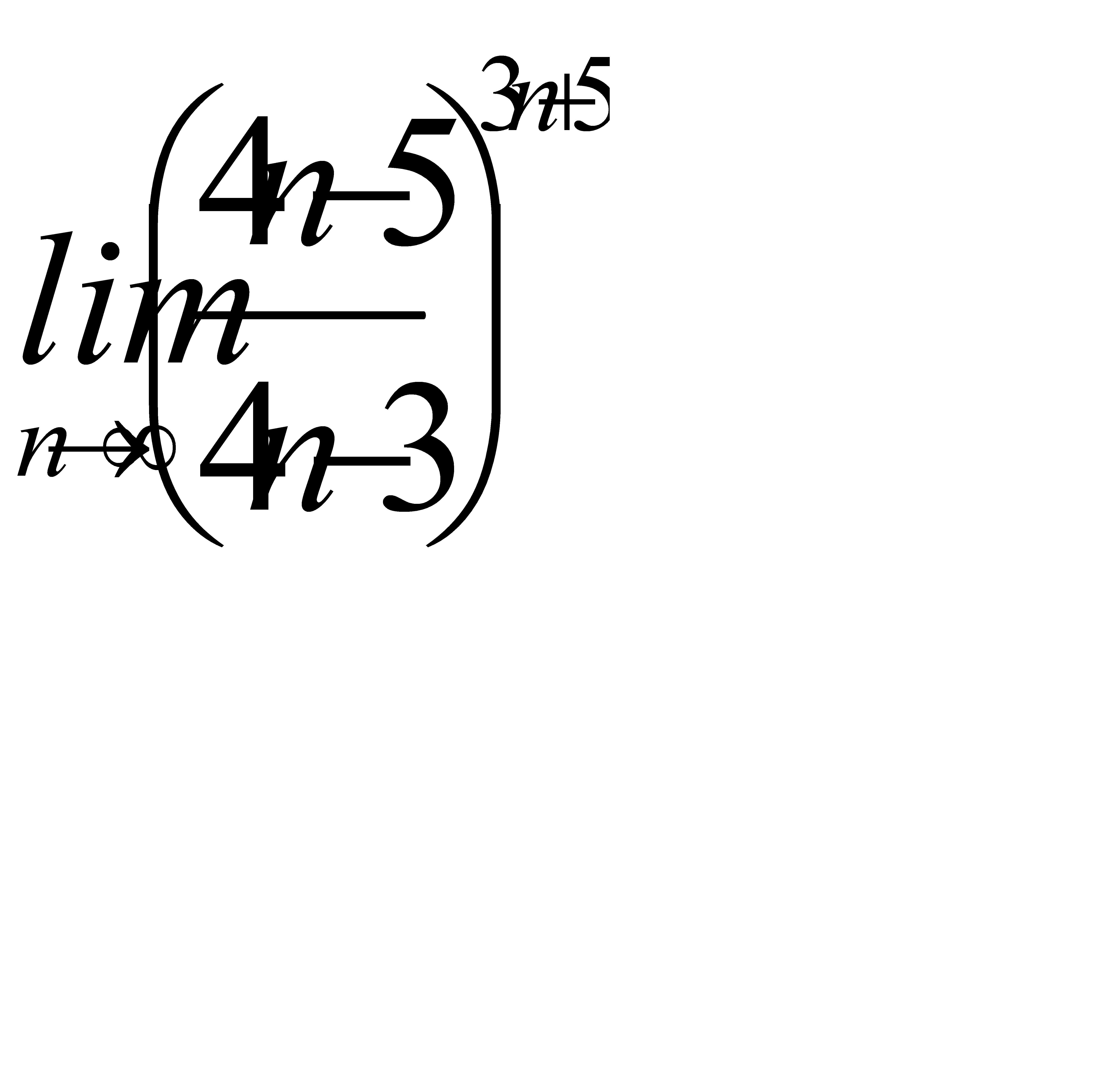
6. 1) 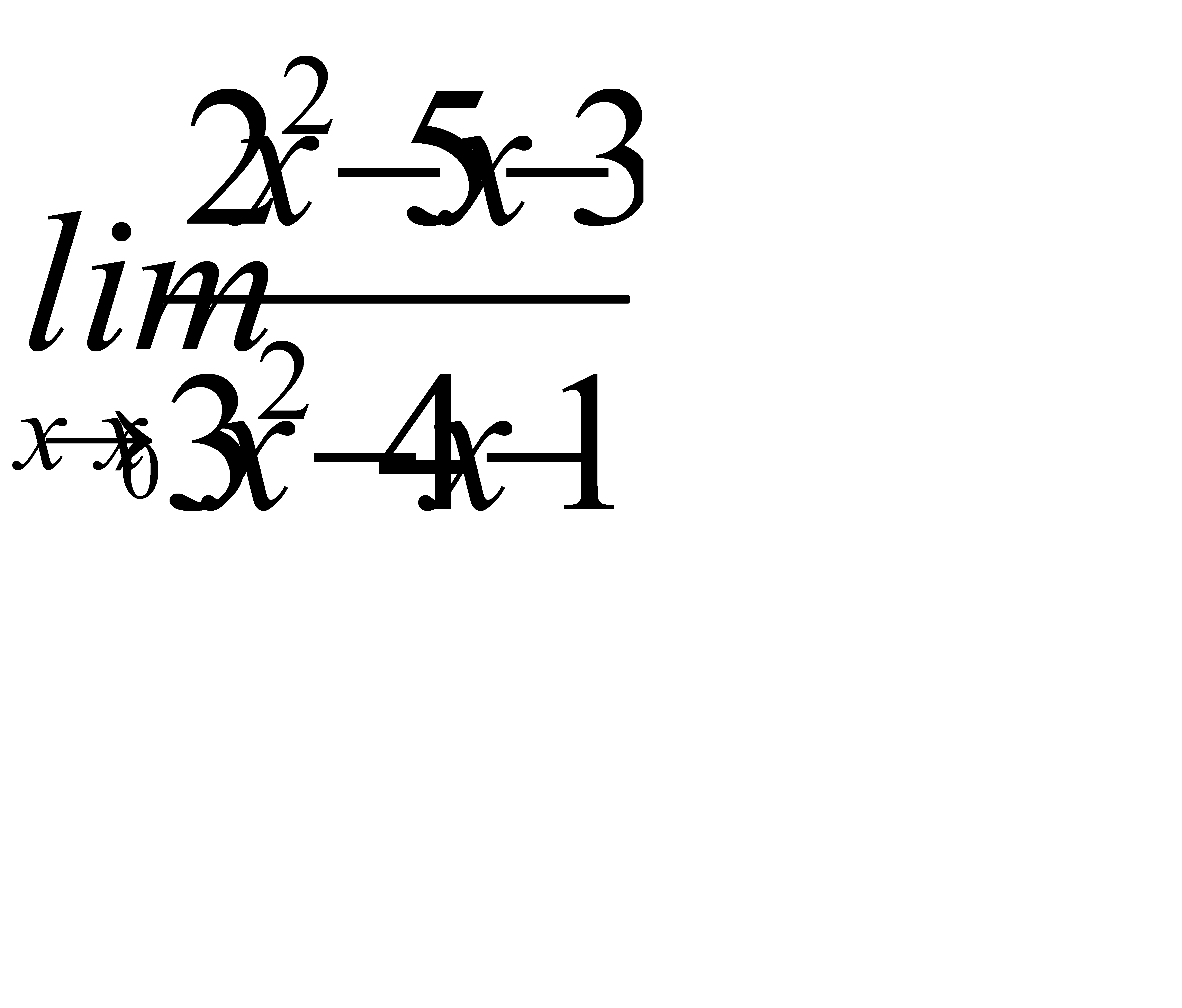 при a)
при a) 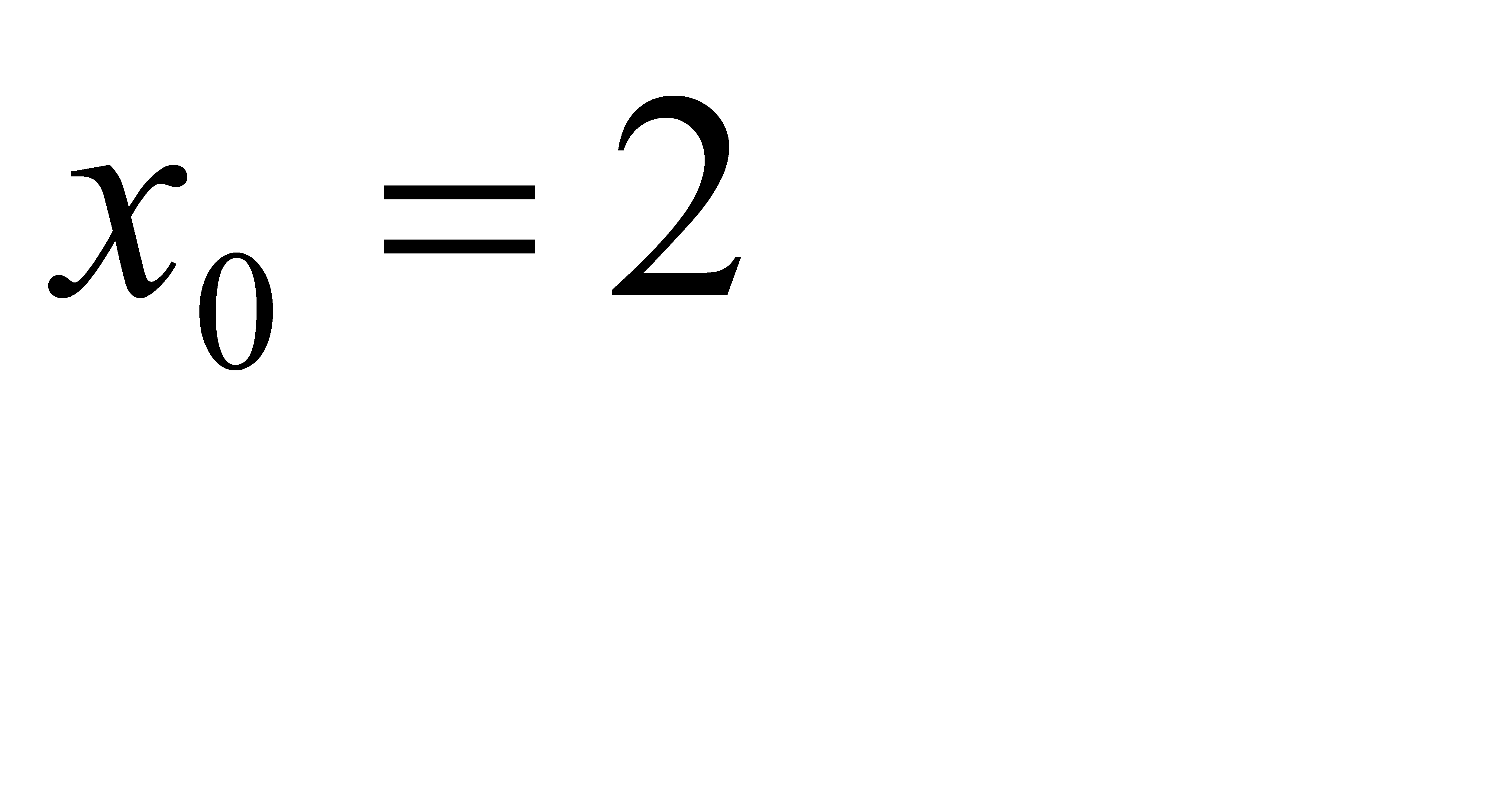 , b)
, b) 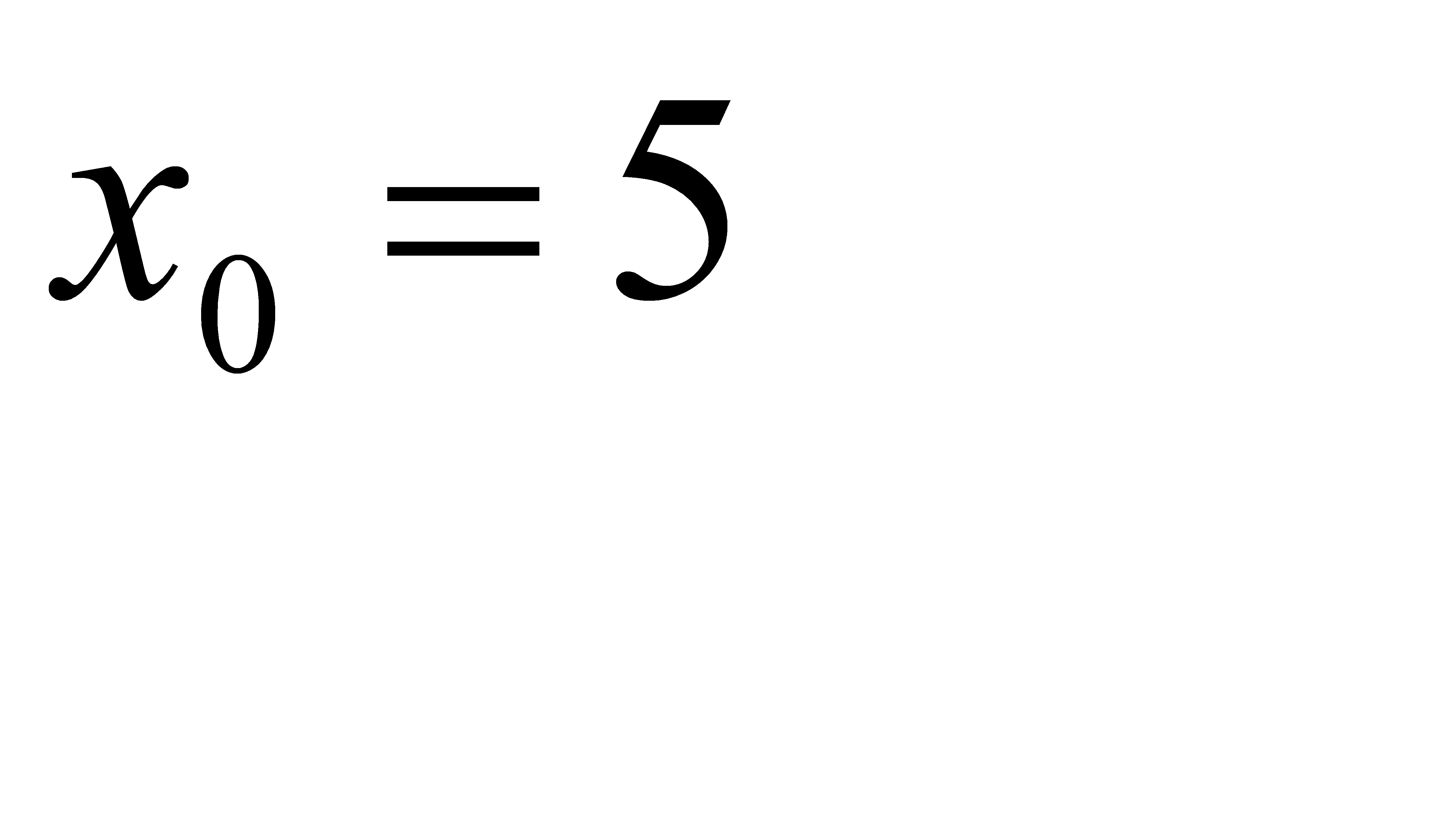 , c)
, c) 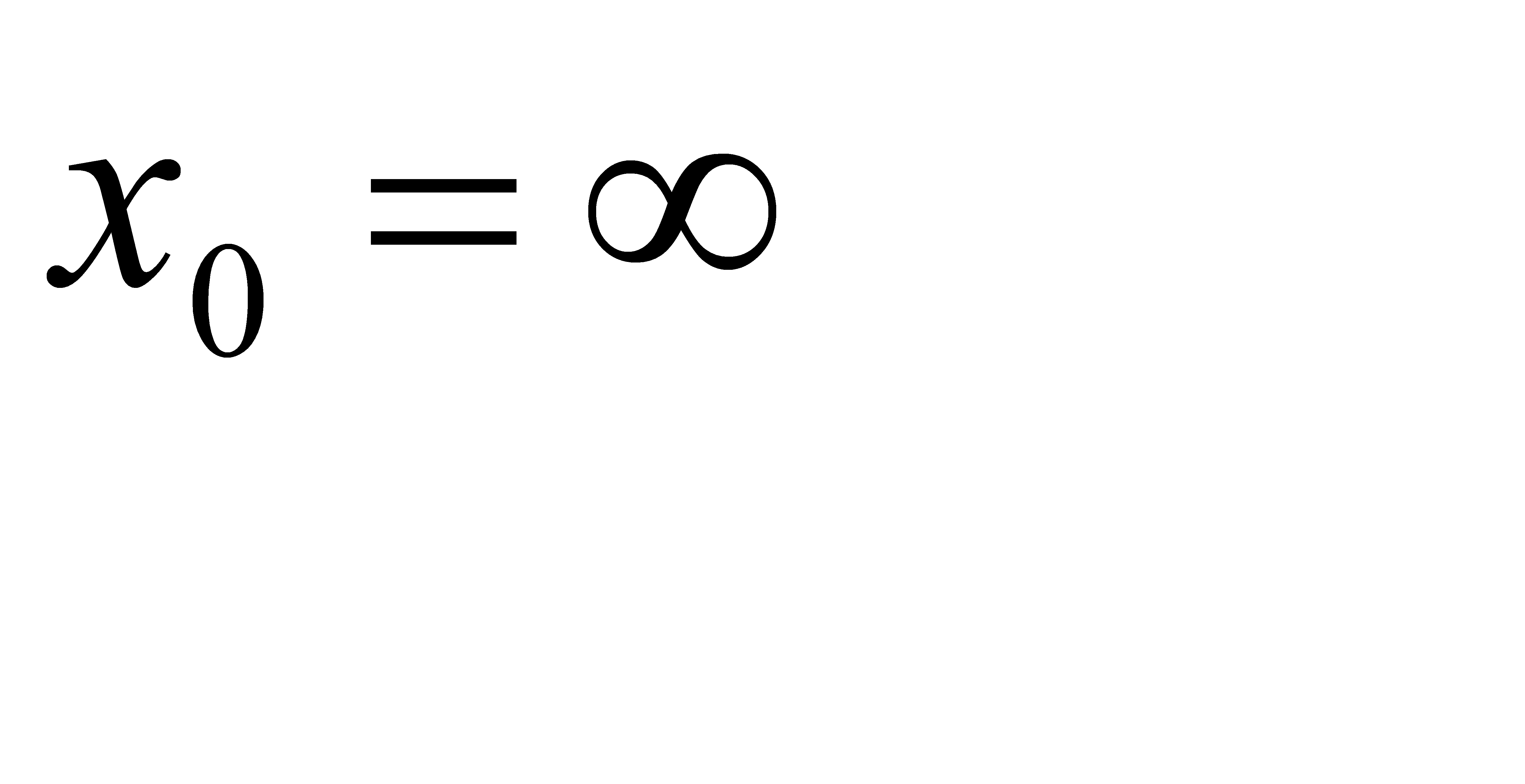 ;
;
2) 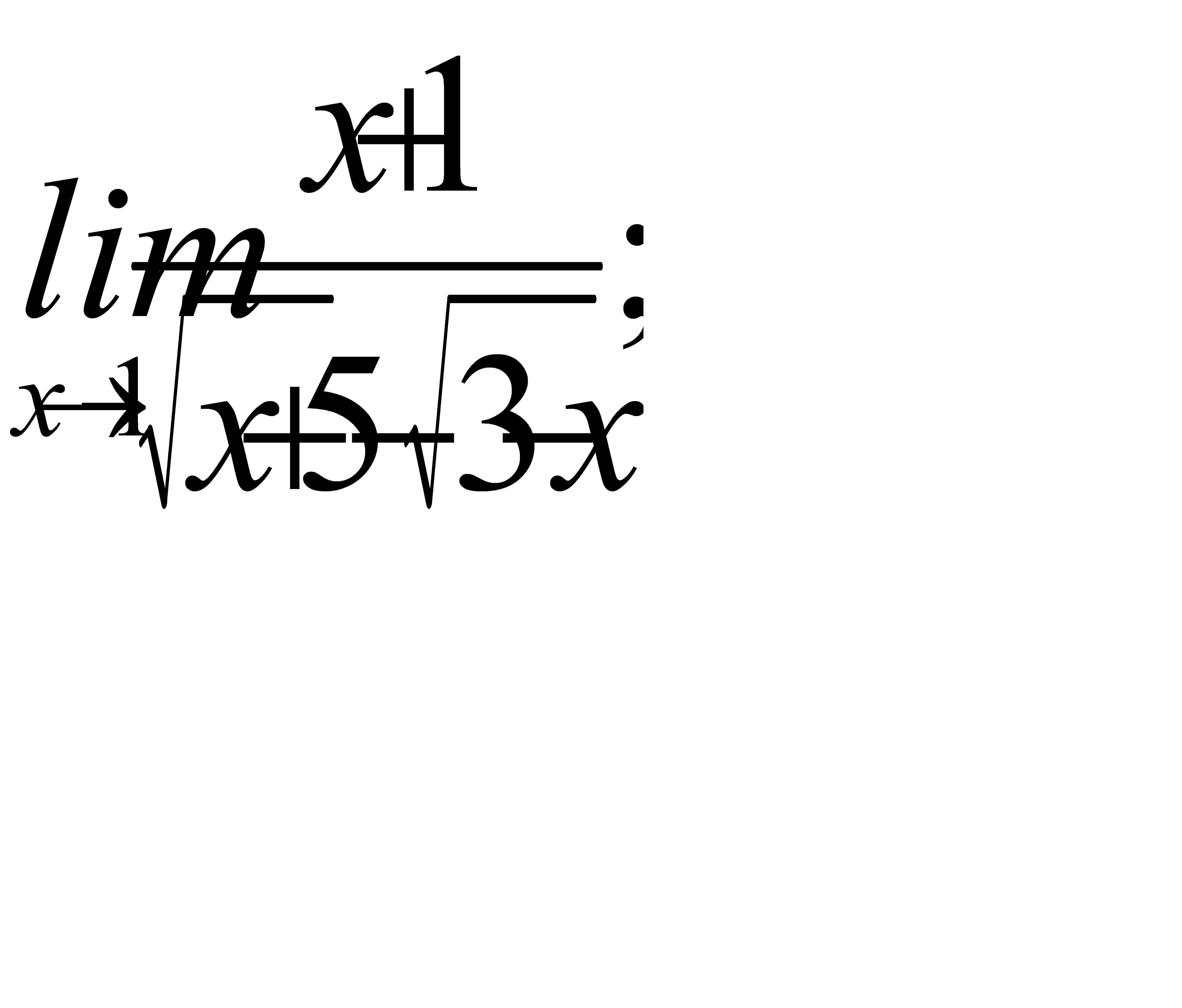 3)
3) 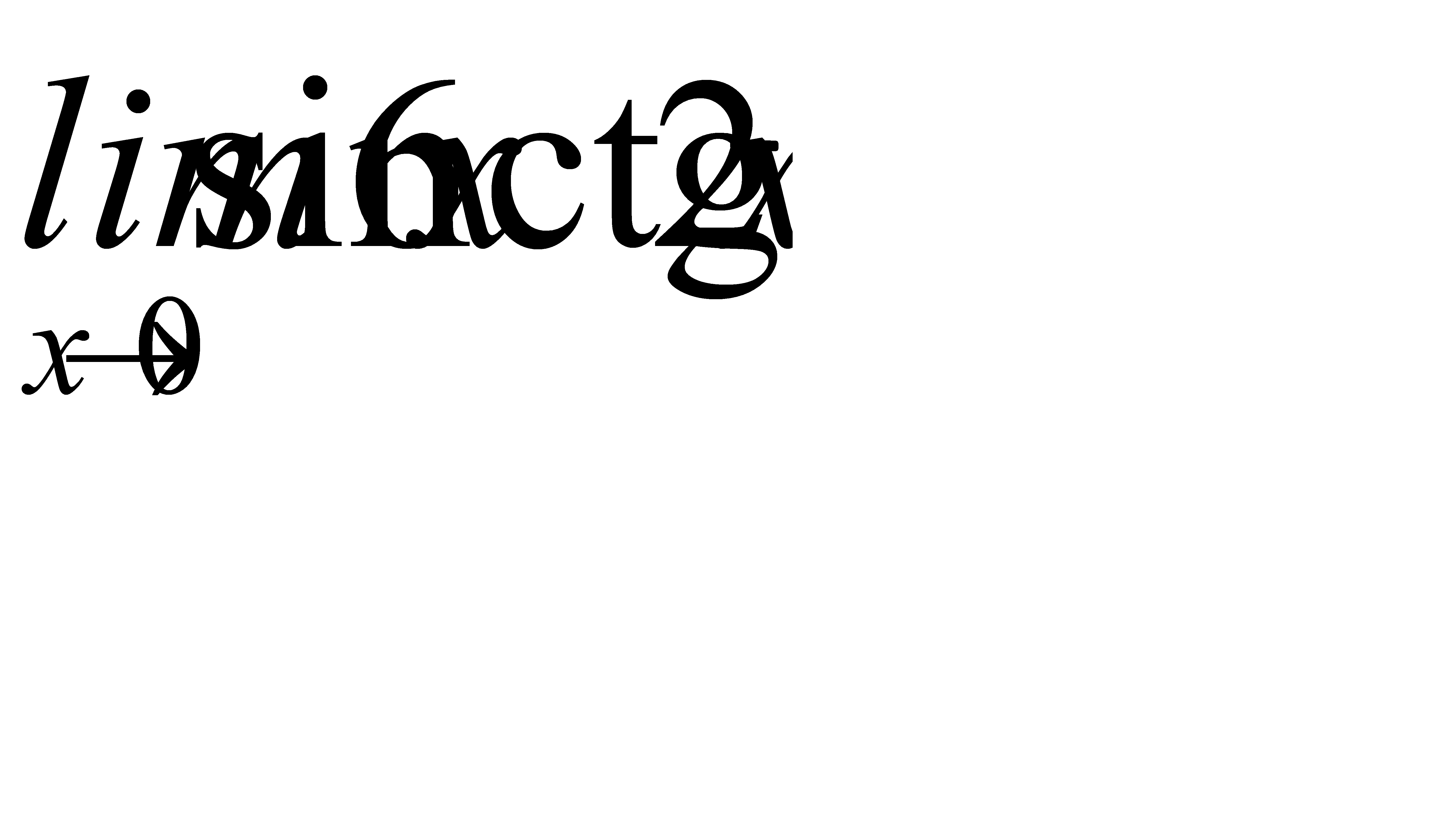 ;
;
4) 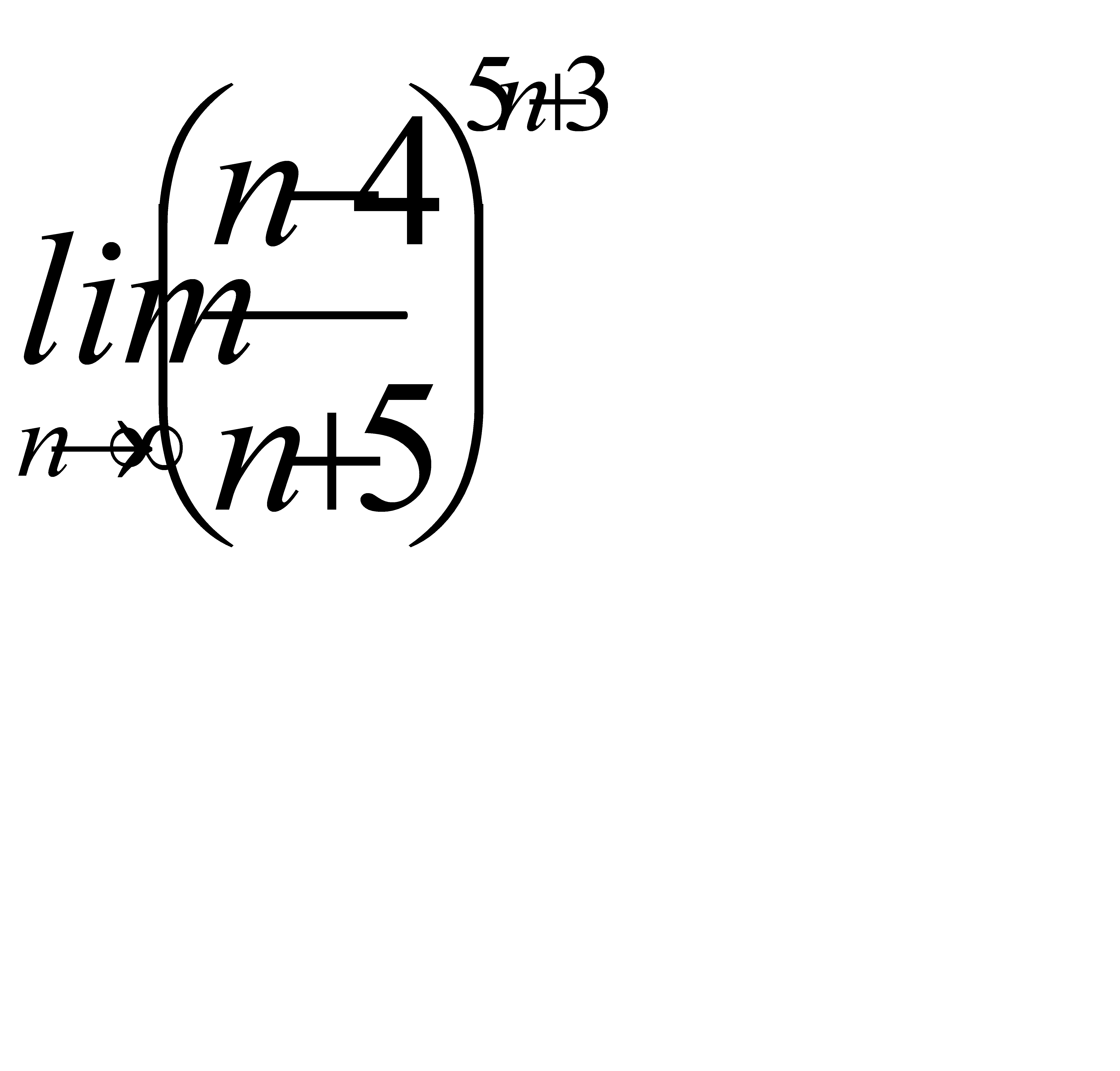
7. 1) 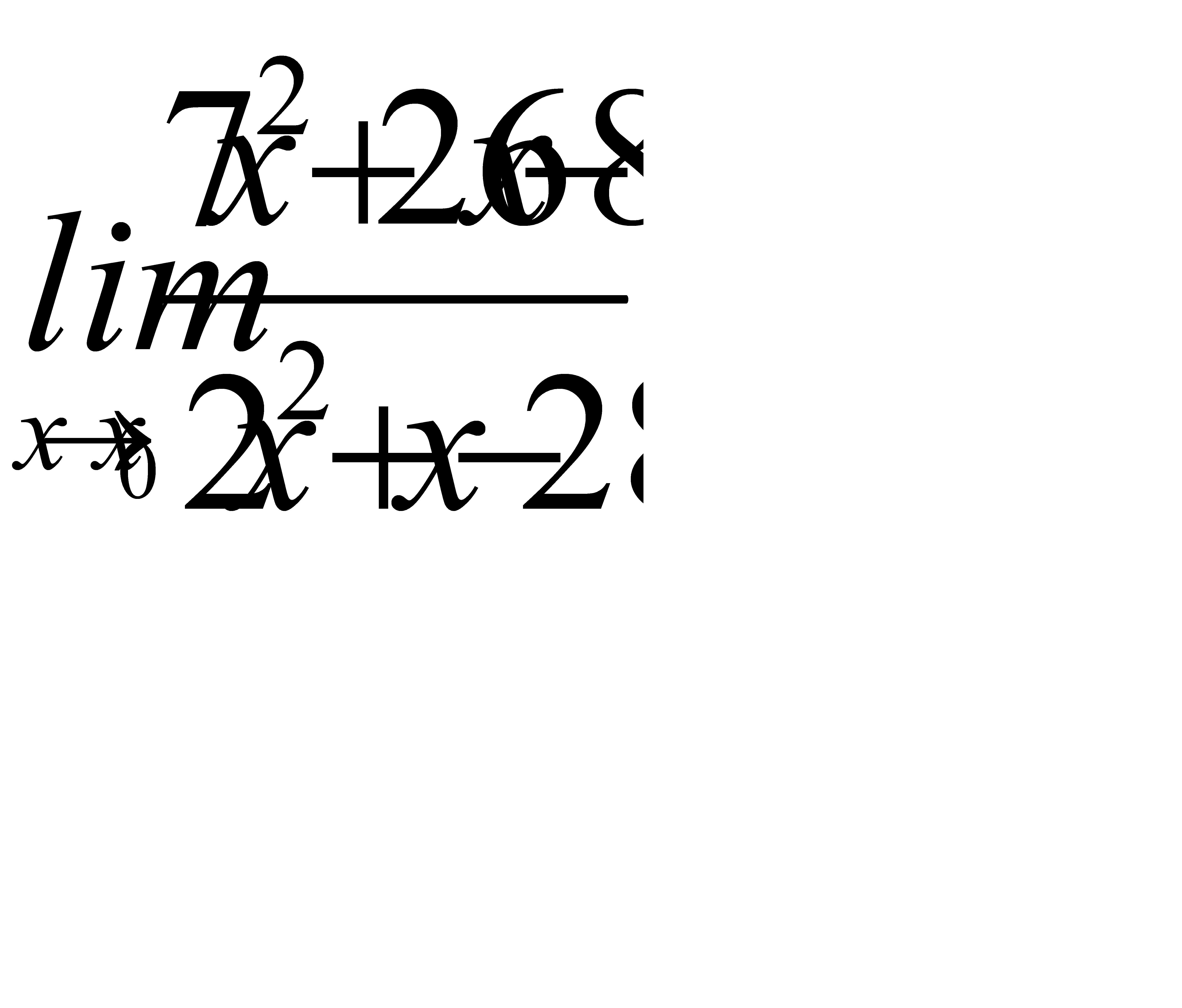 при a)
при a) 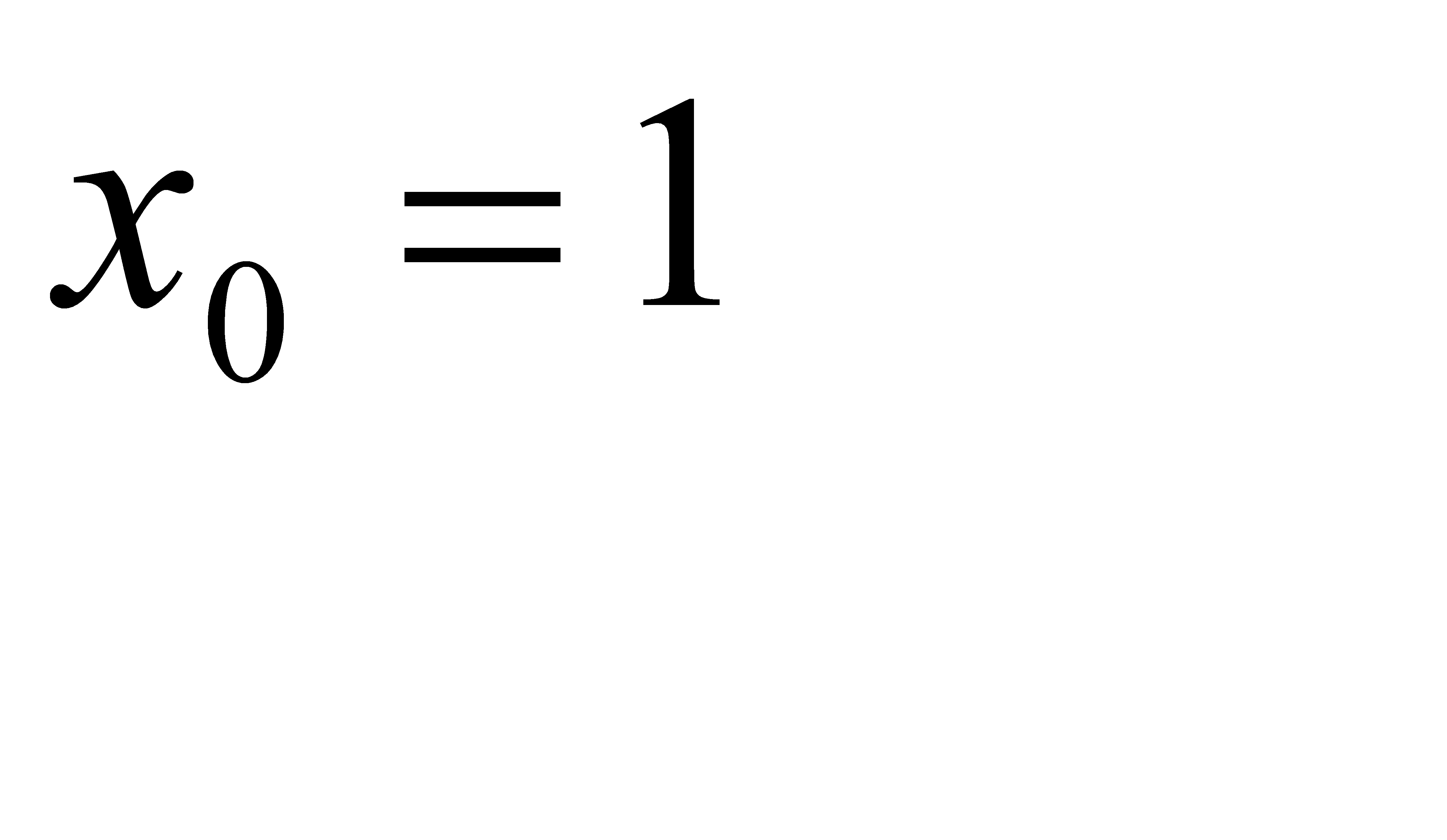 , b)
, b) 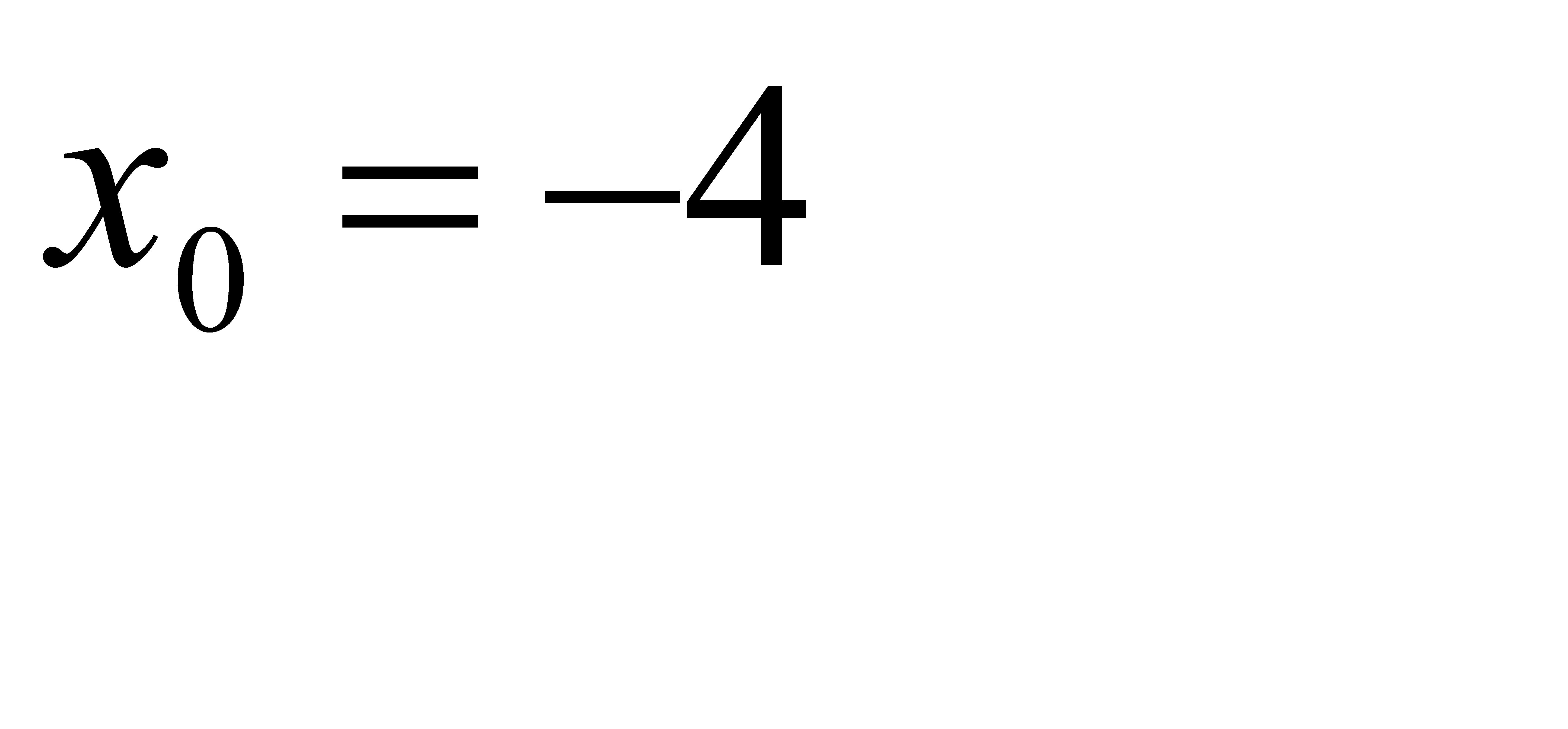 , c)
, c) 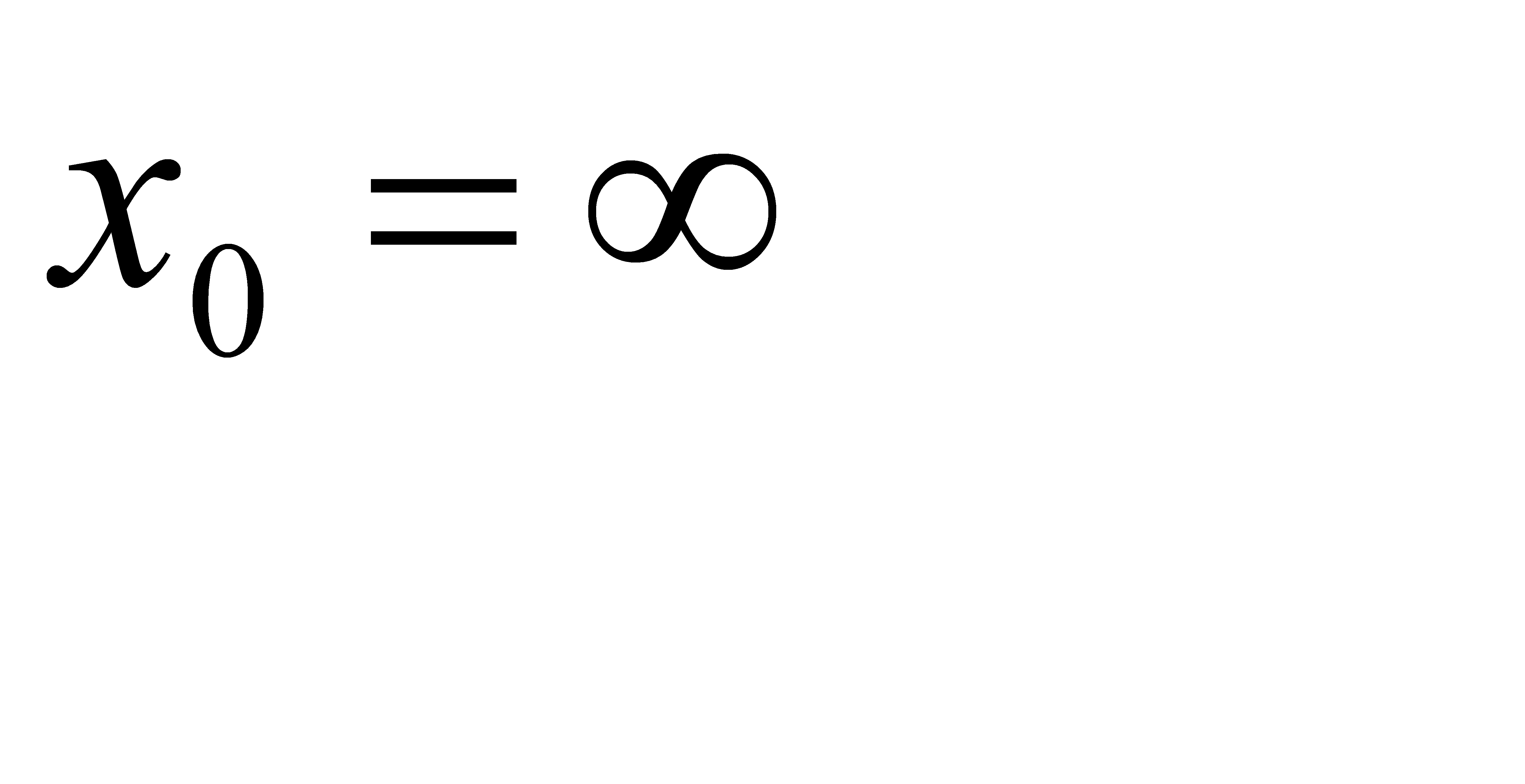 ;
;
2) 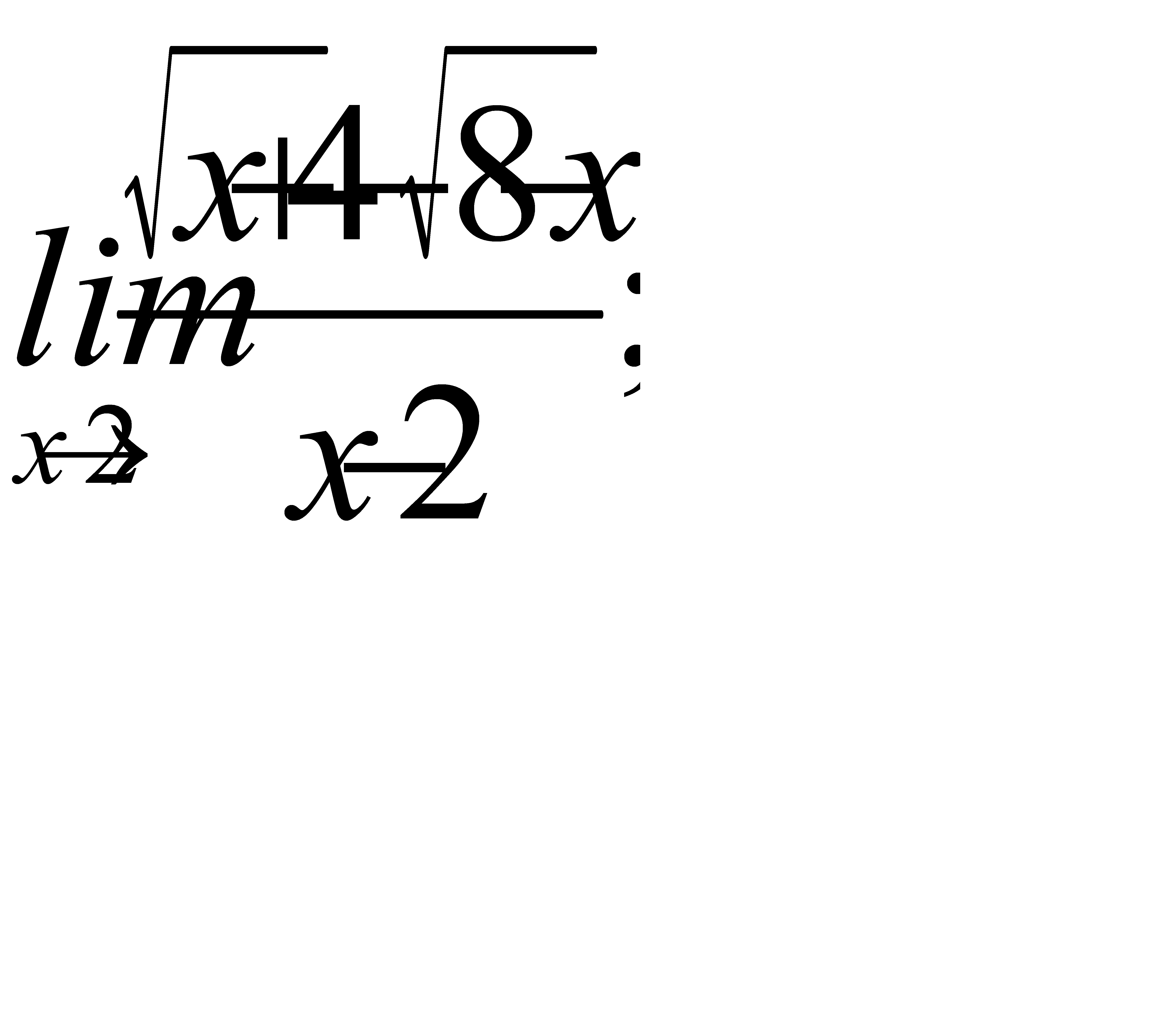 3)
3) 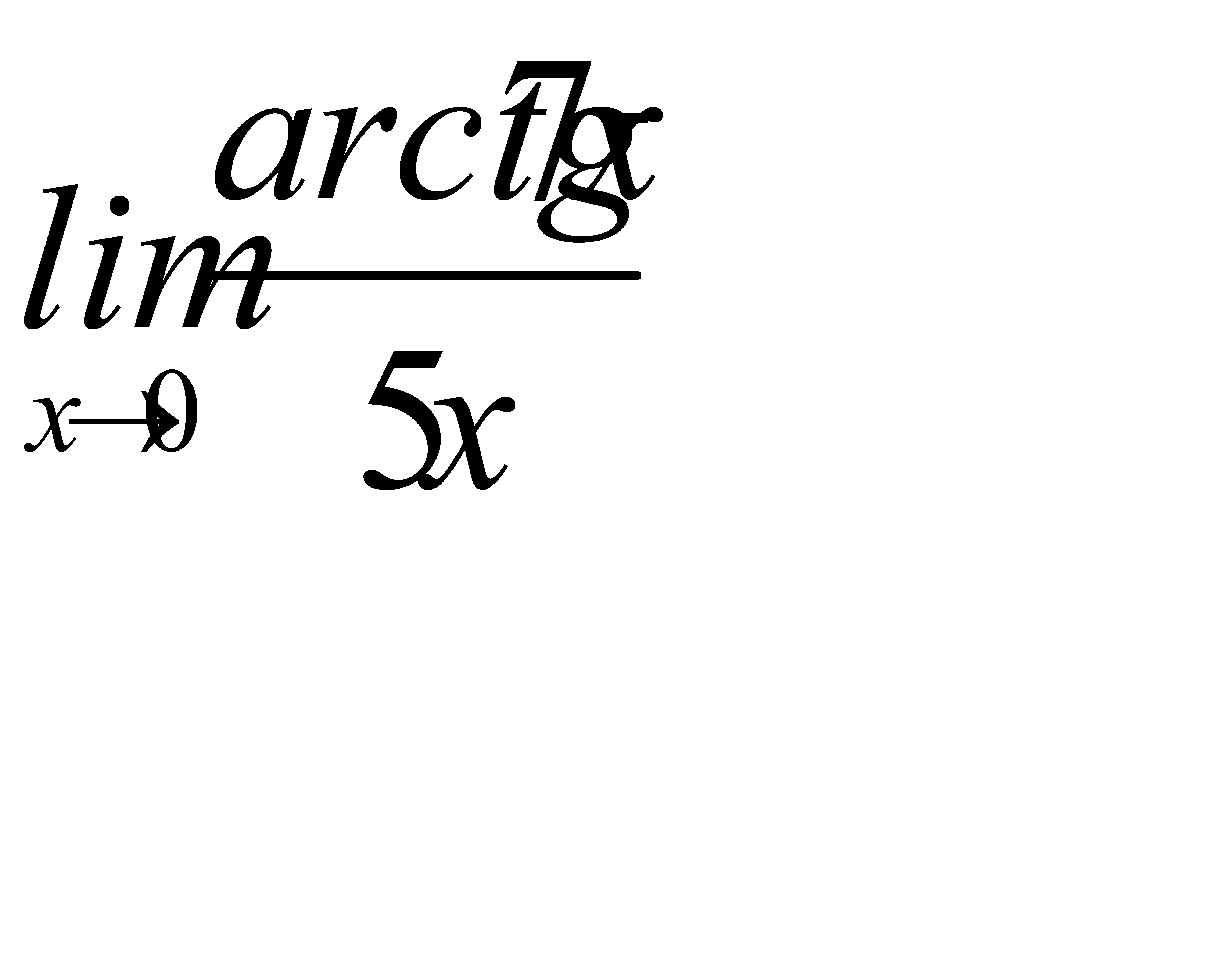 ;
;
4) 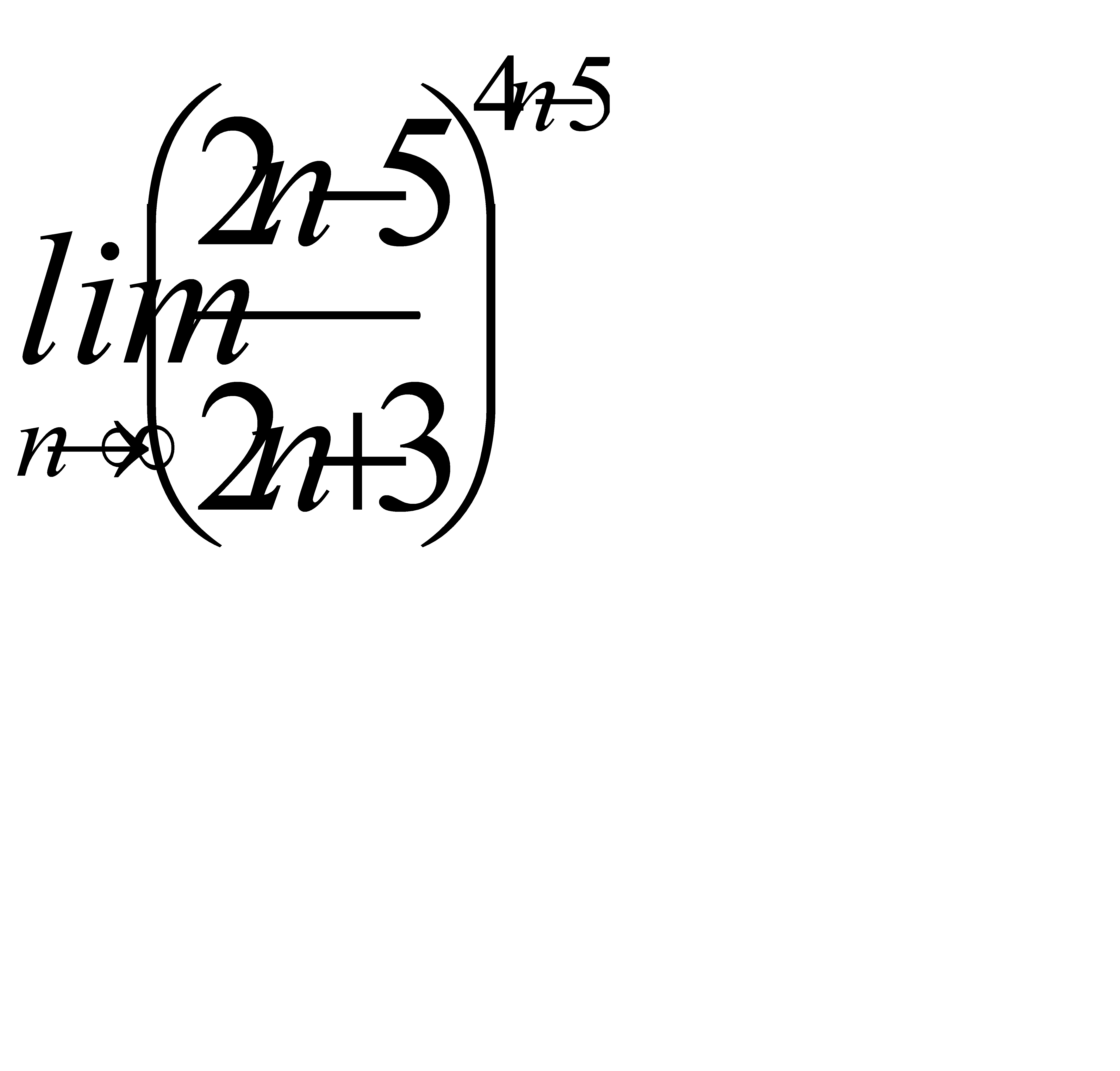
8. 1) 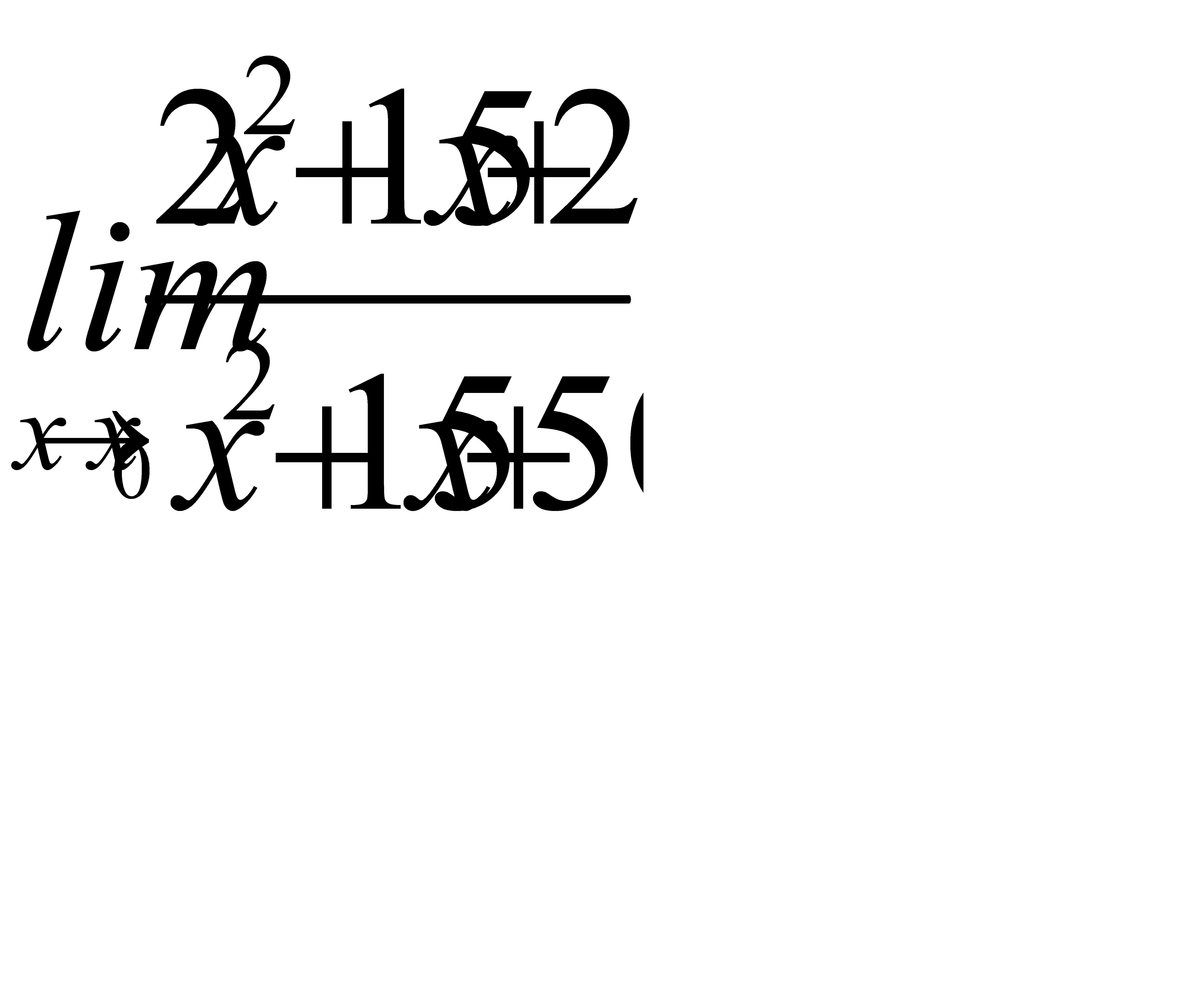 при a)
при a) 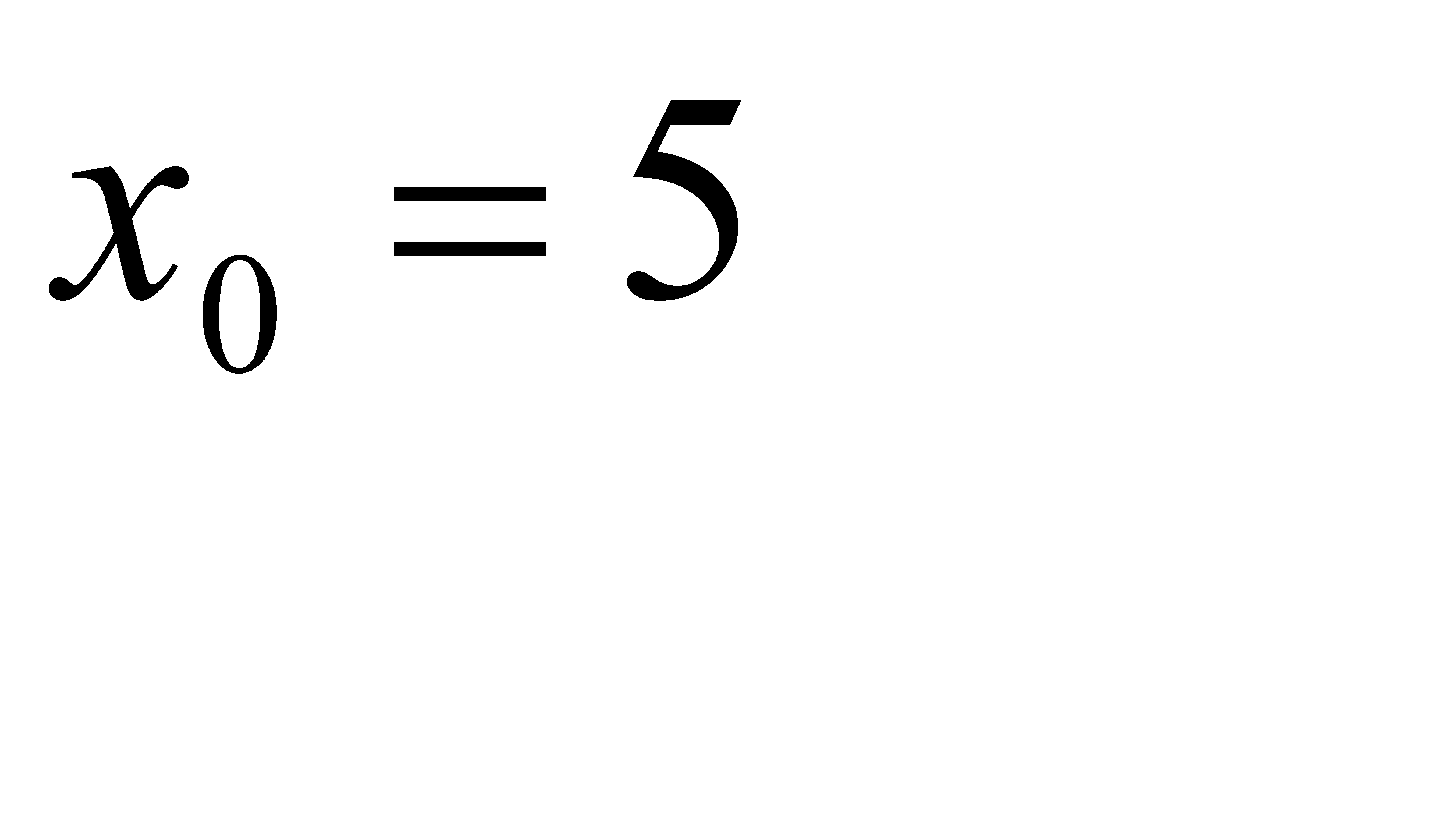 , b)
, b) 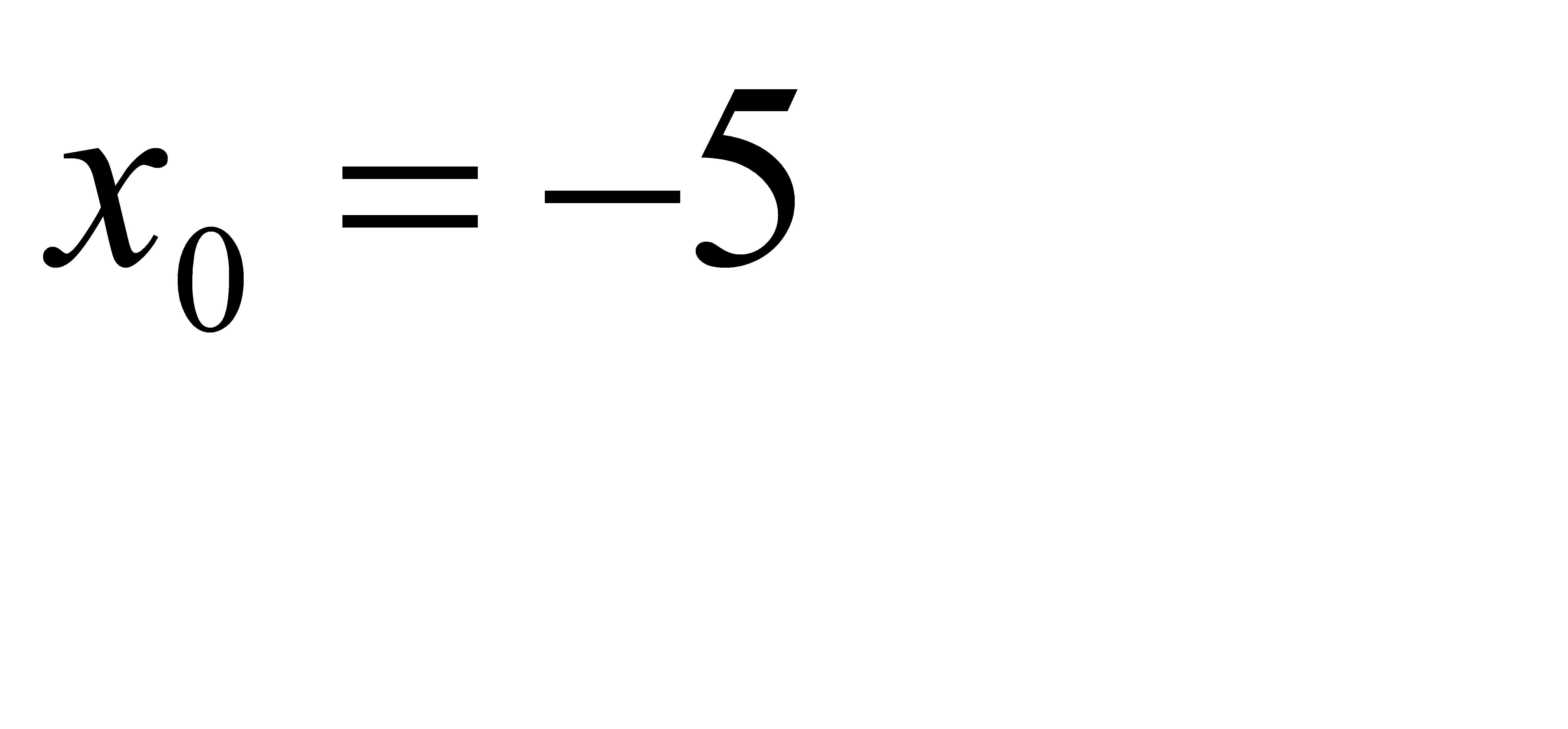 , c)
, c) 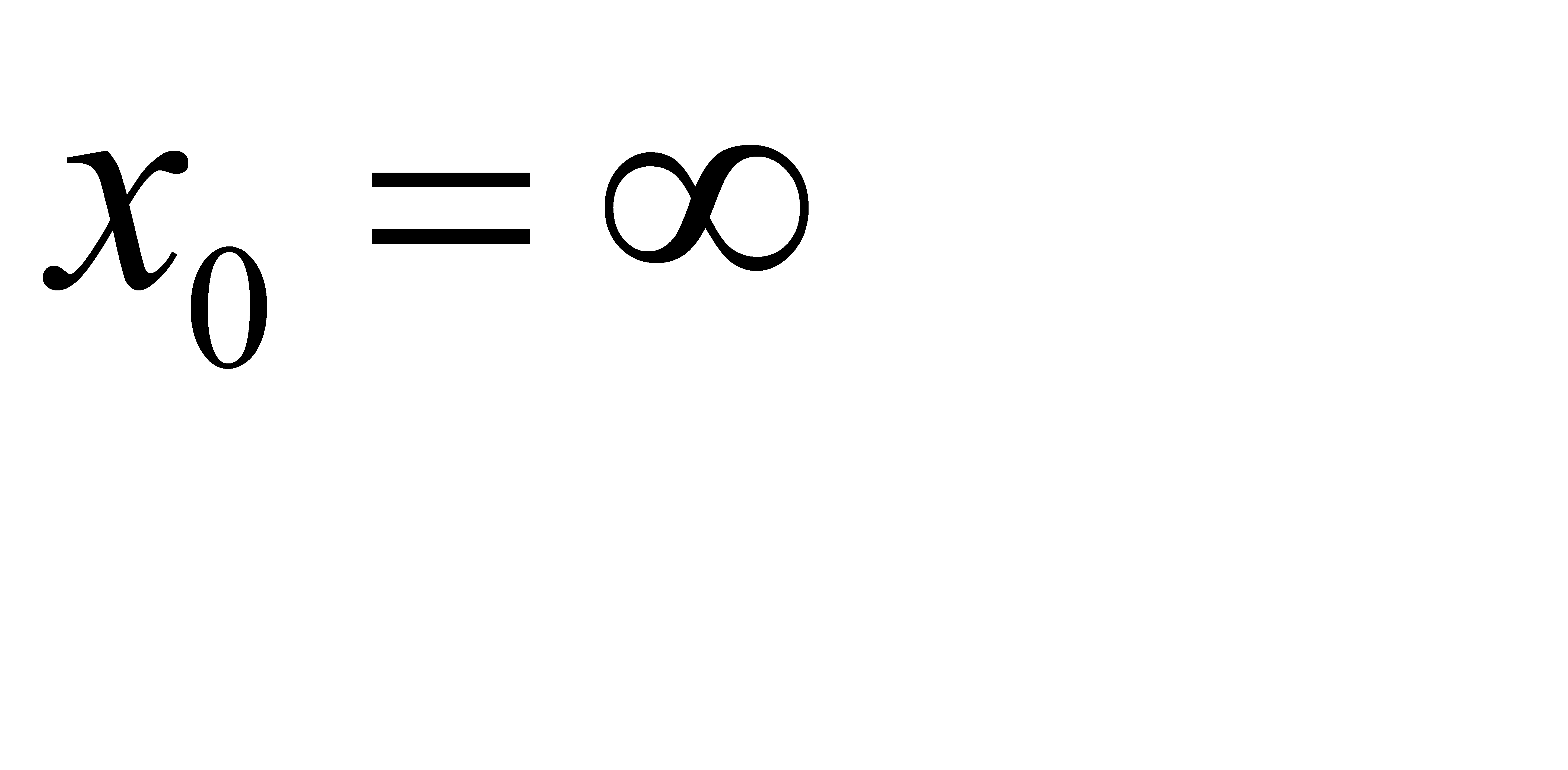 ;
;
2) 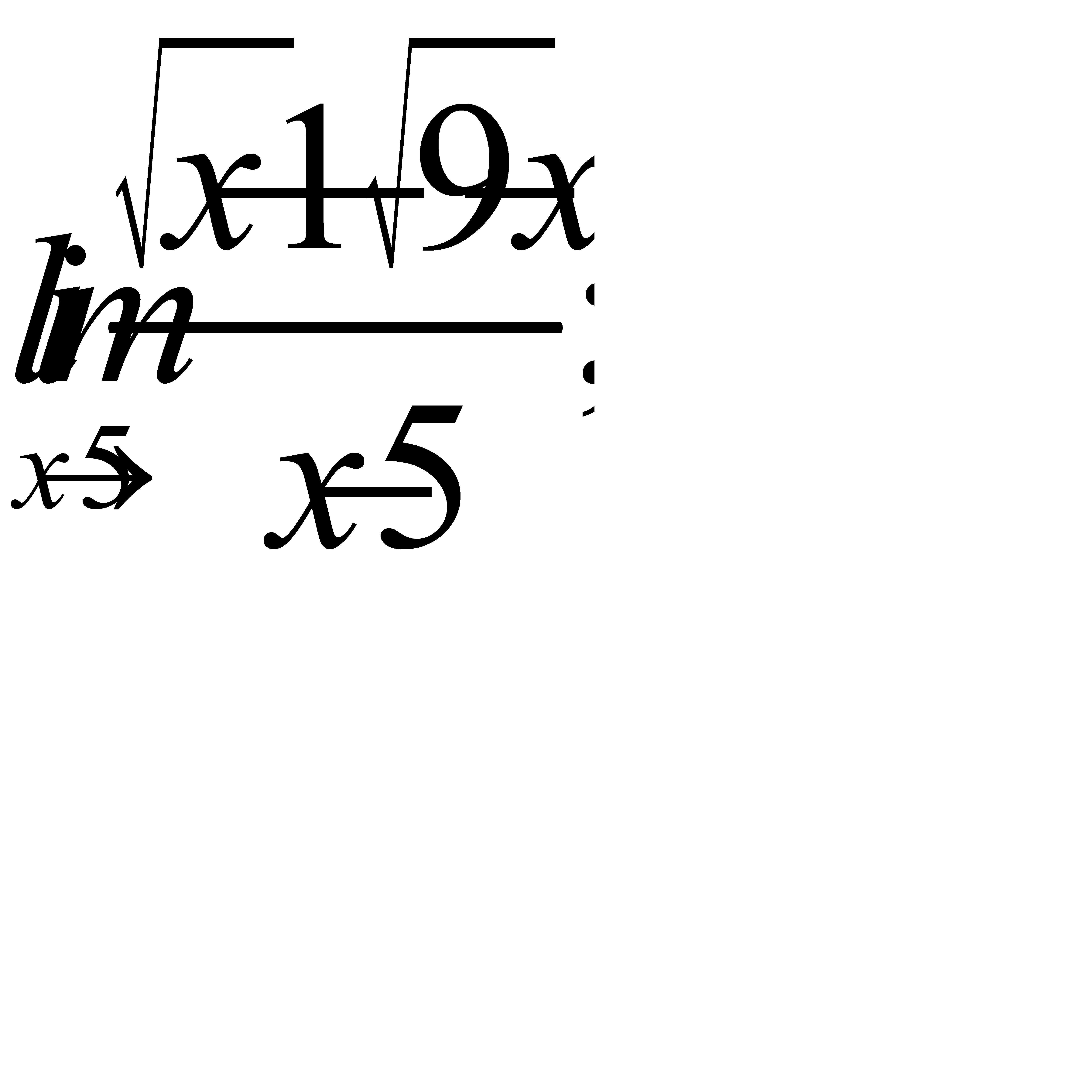 3)
3) 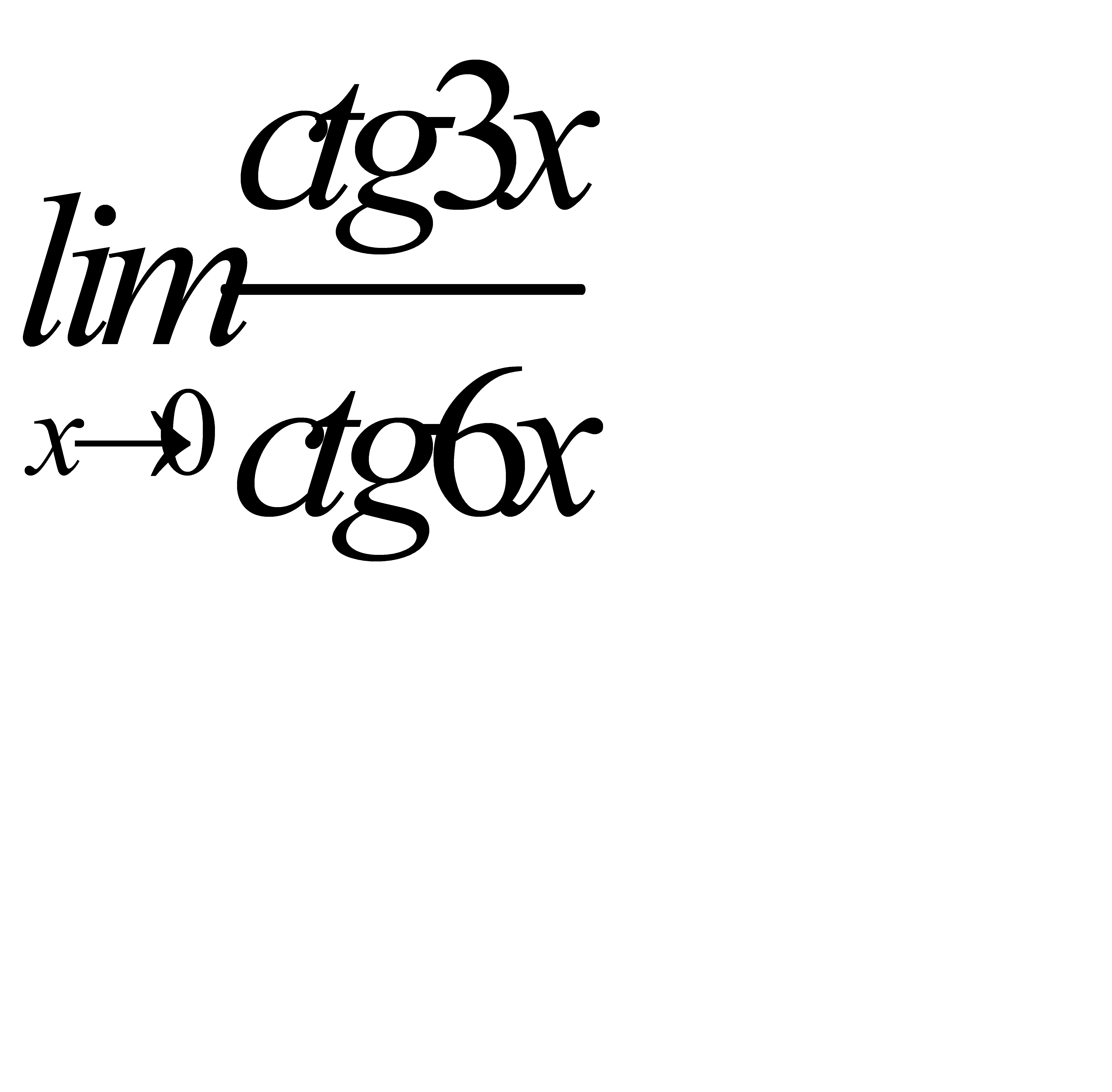 ;
;
4) 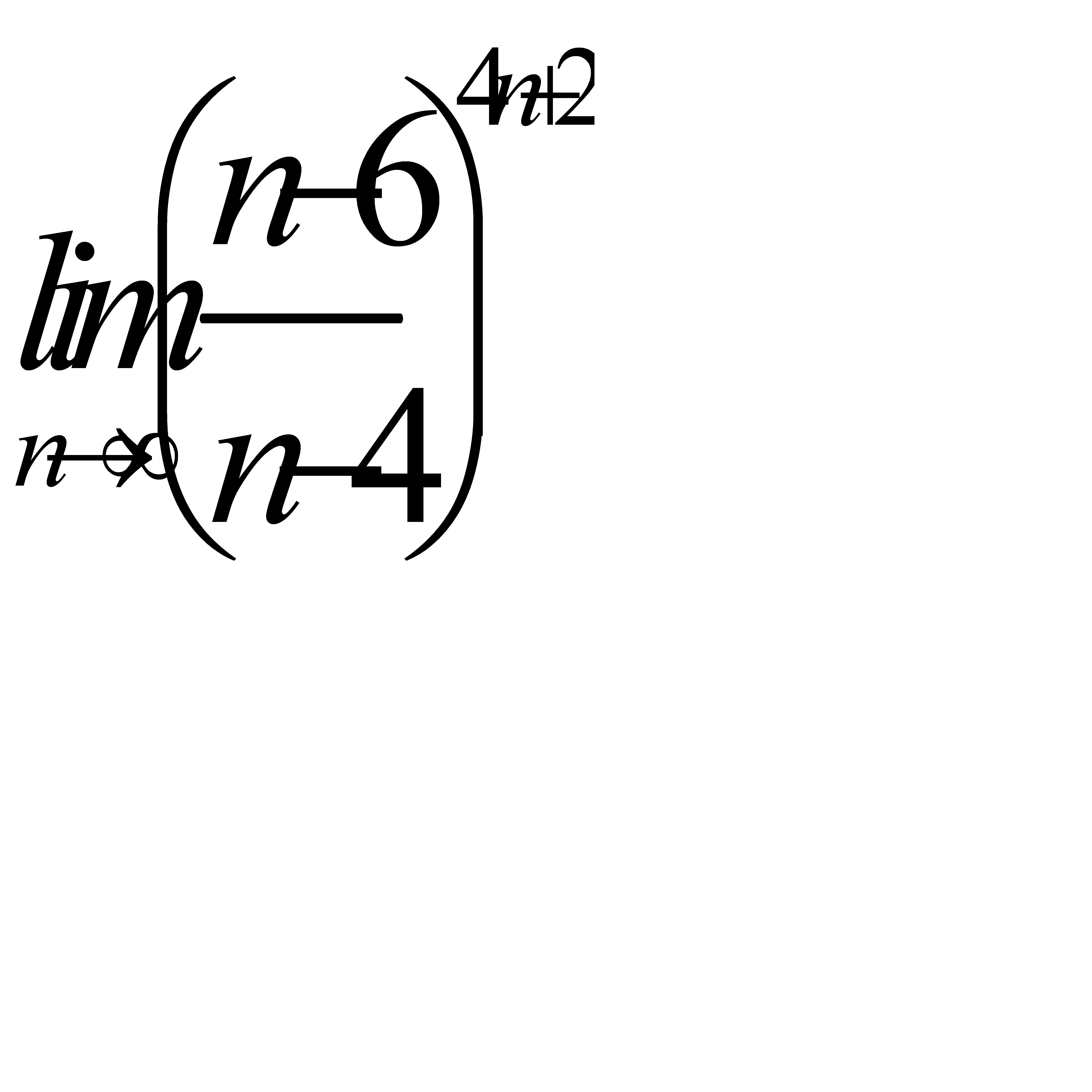
9. 1) 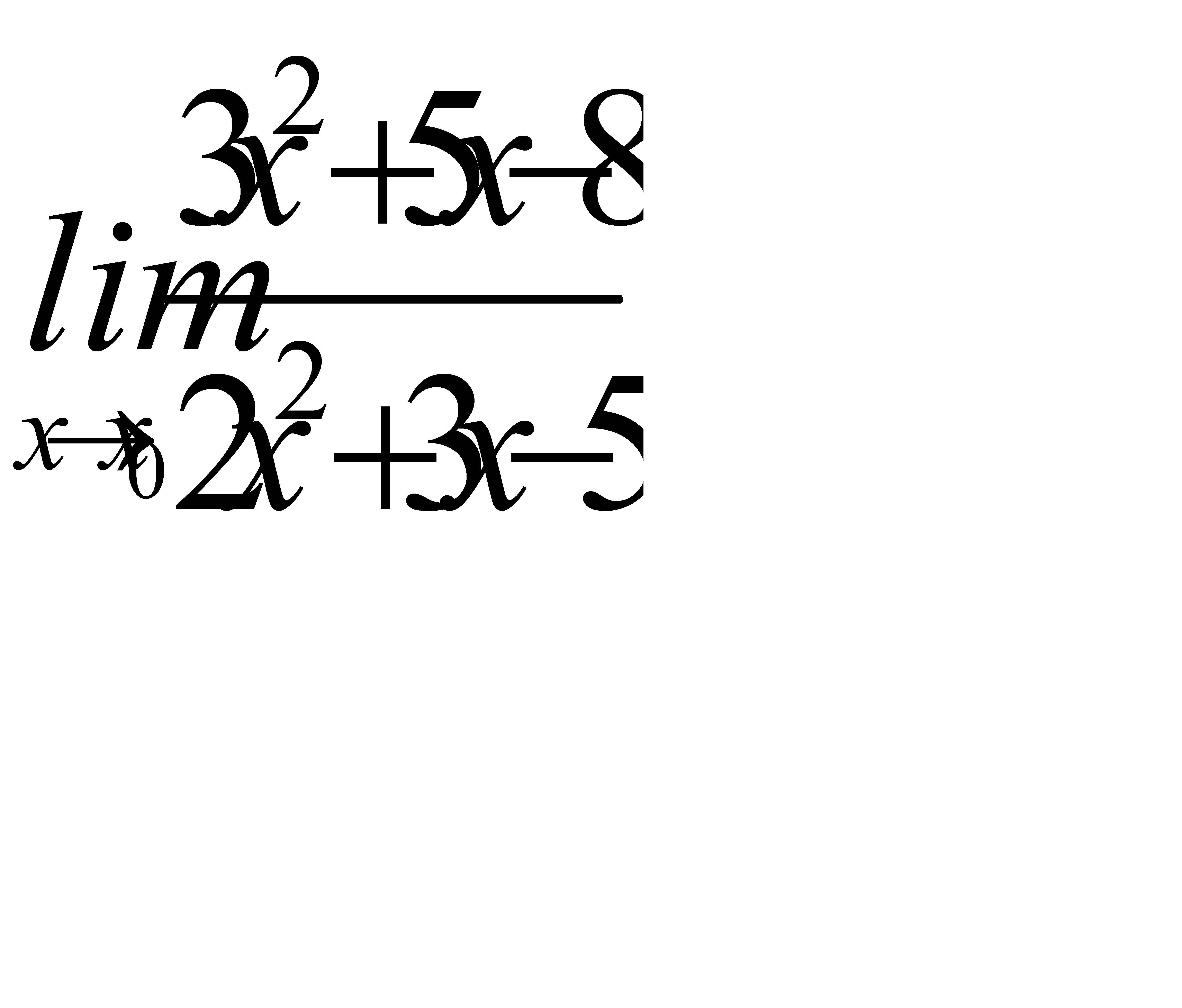 при a)
при a) 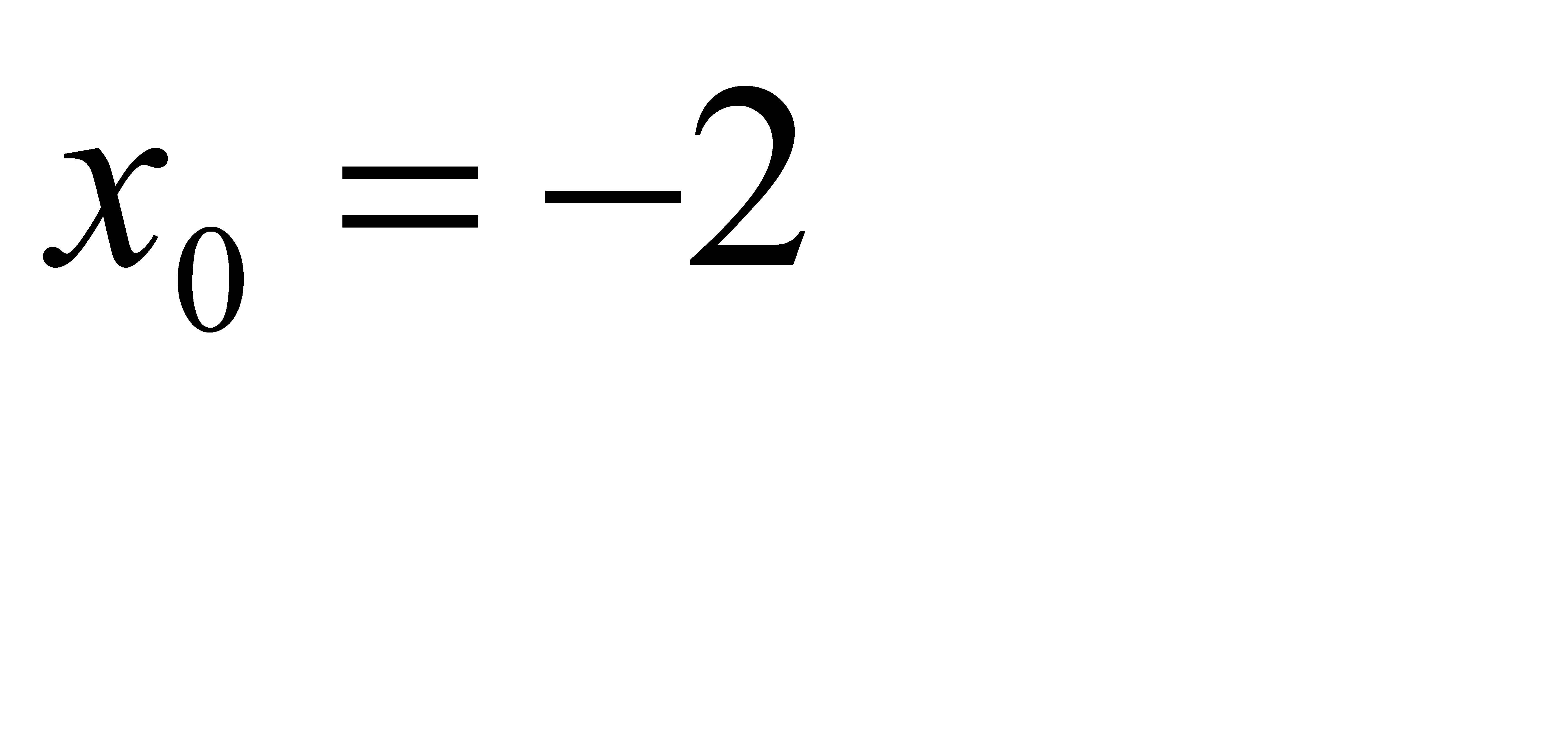 , b)
, b) 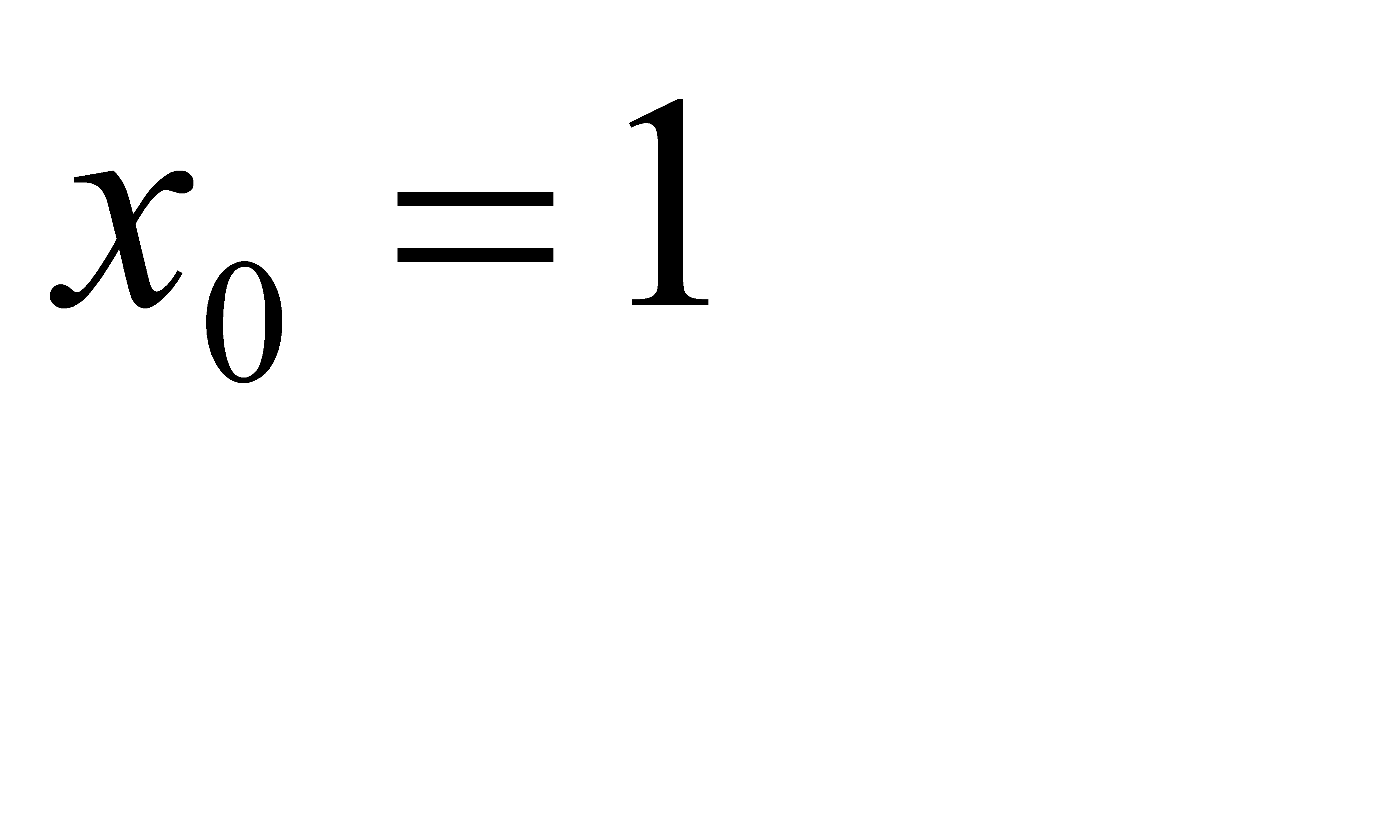 , c)
, c) 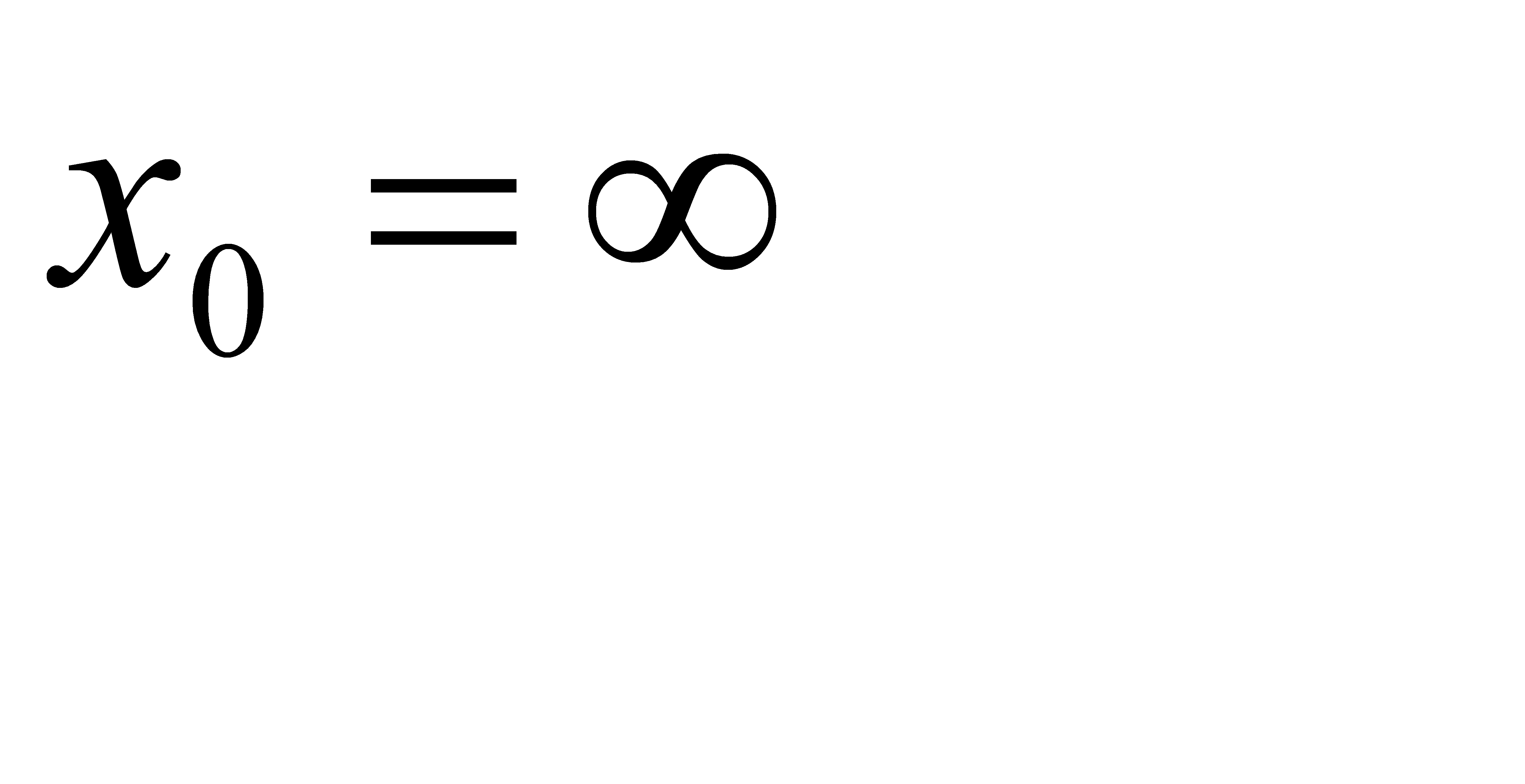 ;
;
2) 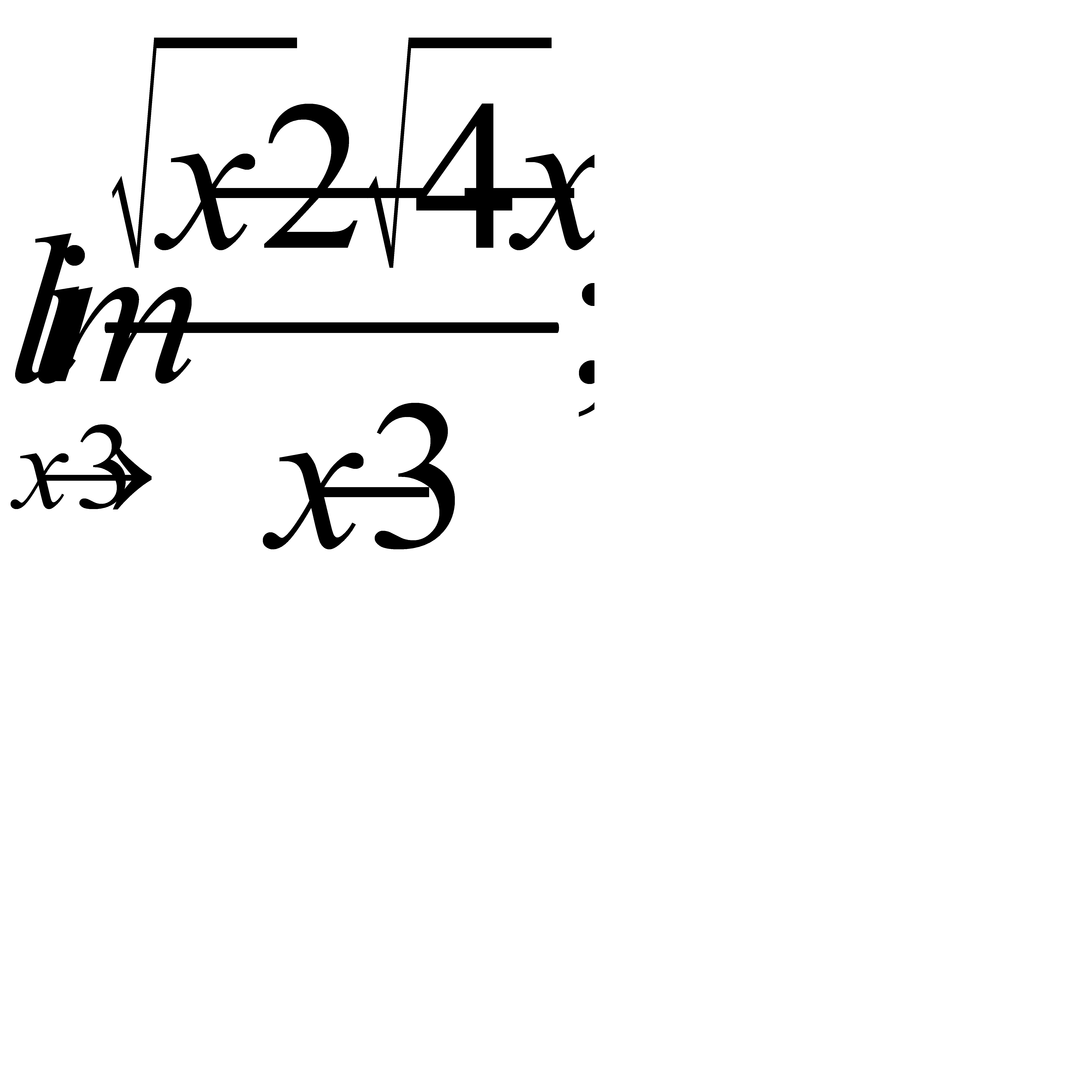 3)
3) 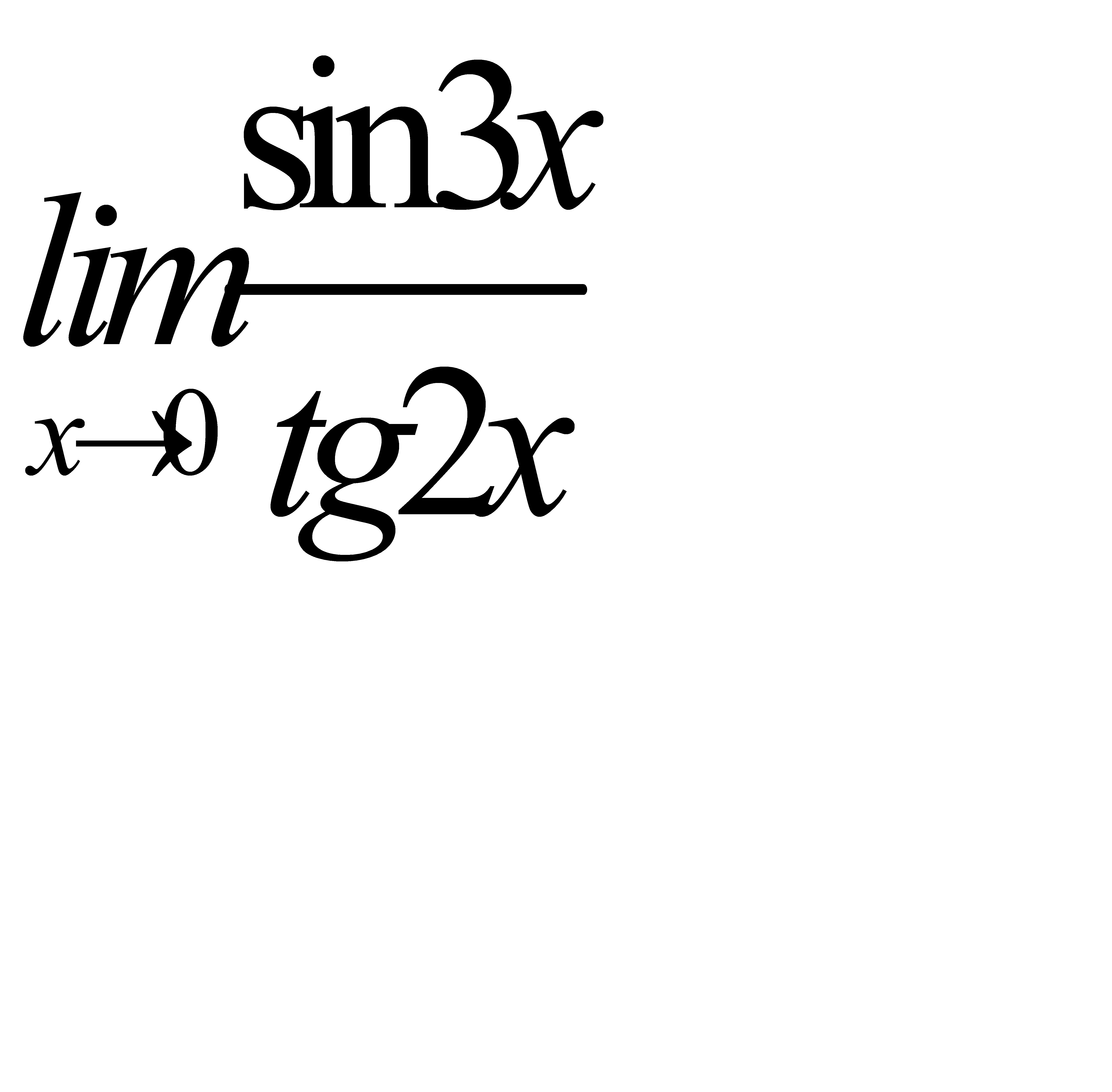 ;
;
4) 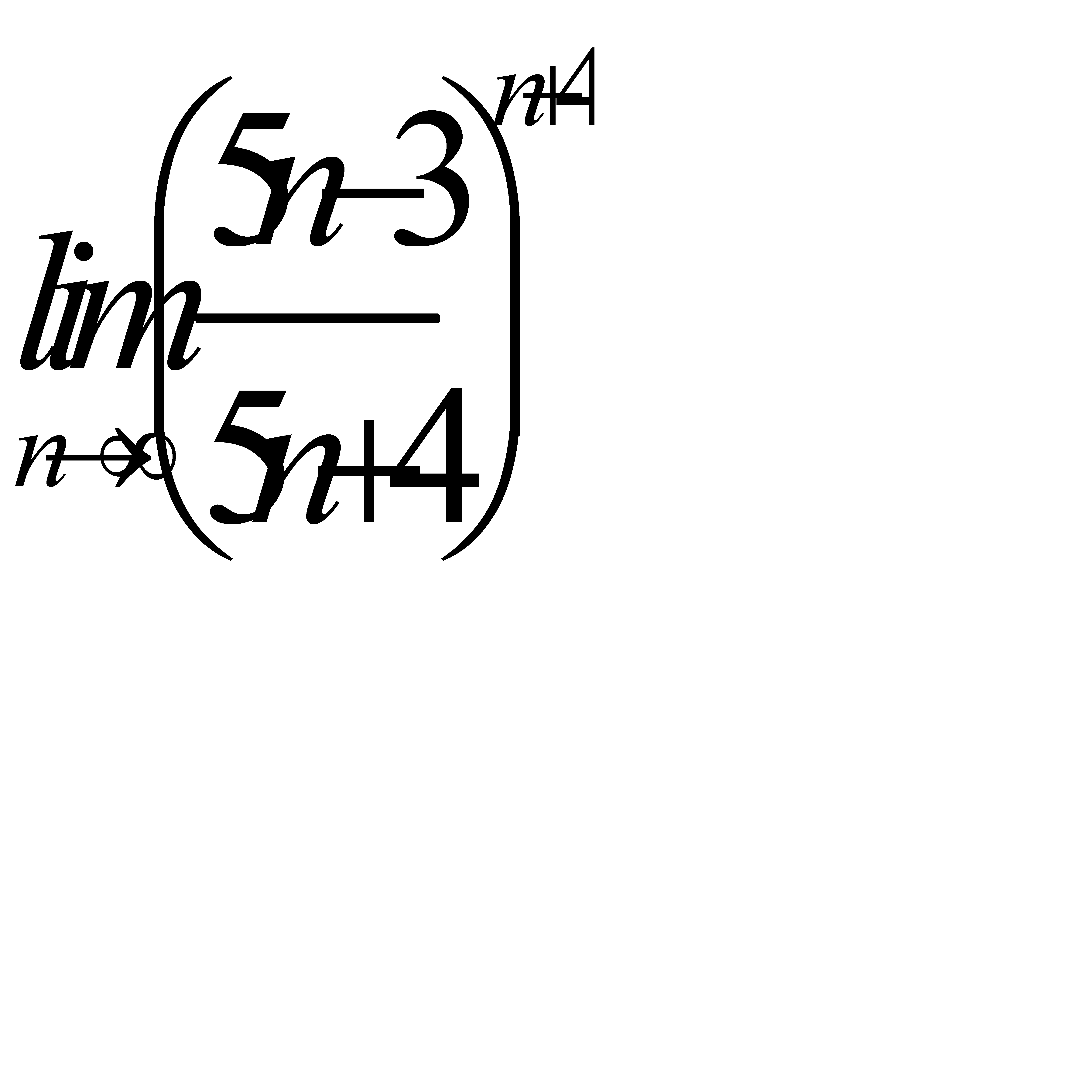
10. 1) 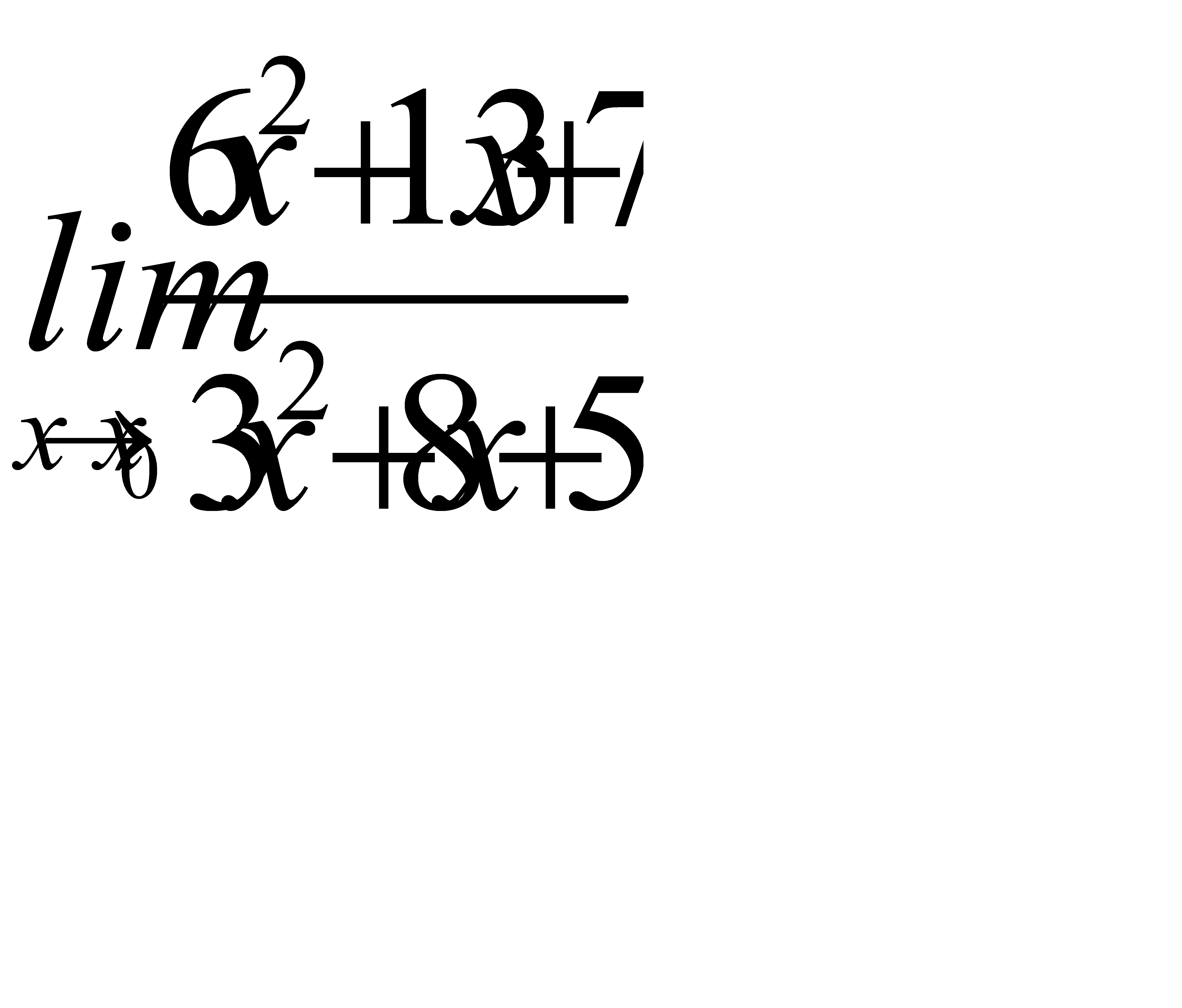 при a)
при a) 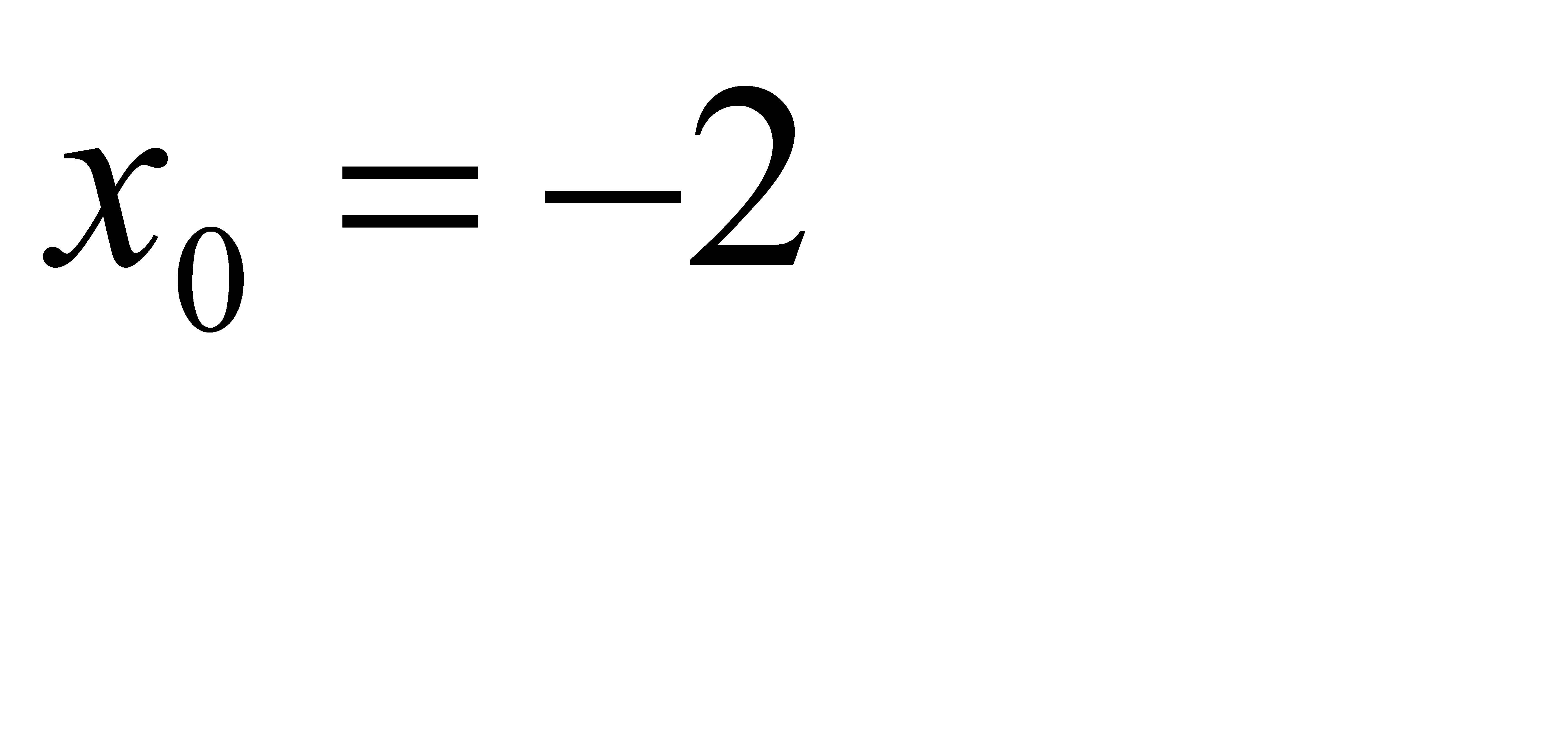 , b)
, b) 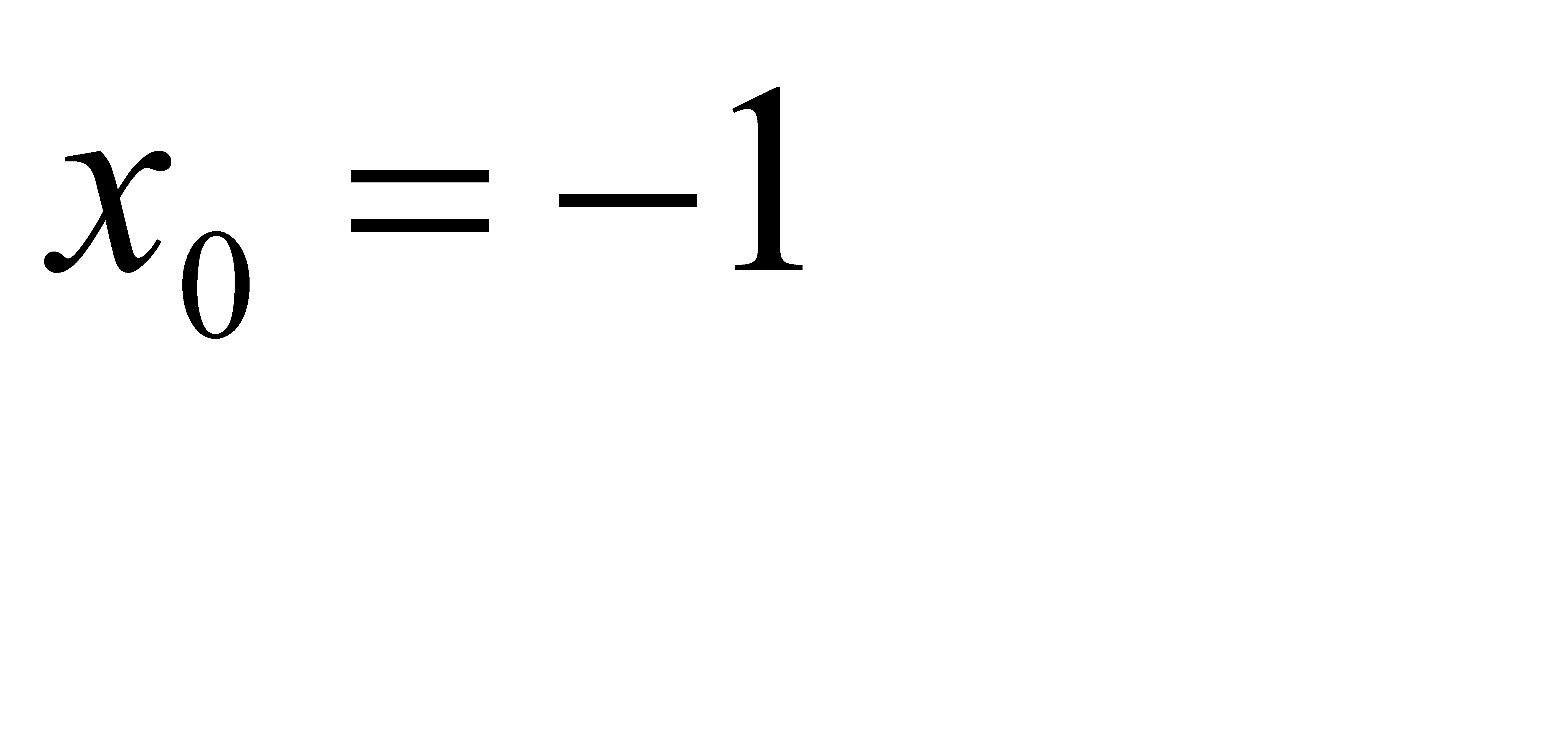 , c)
, c) 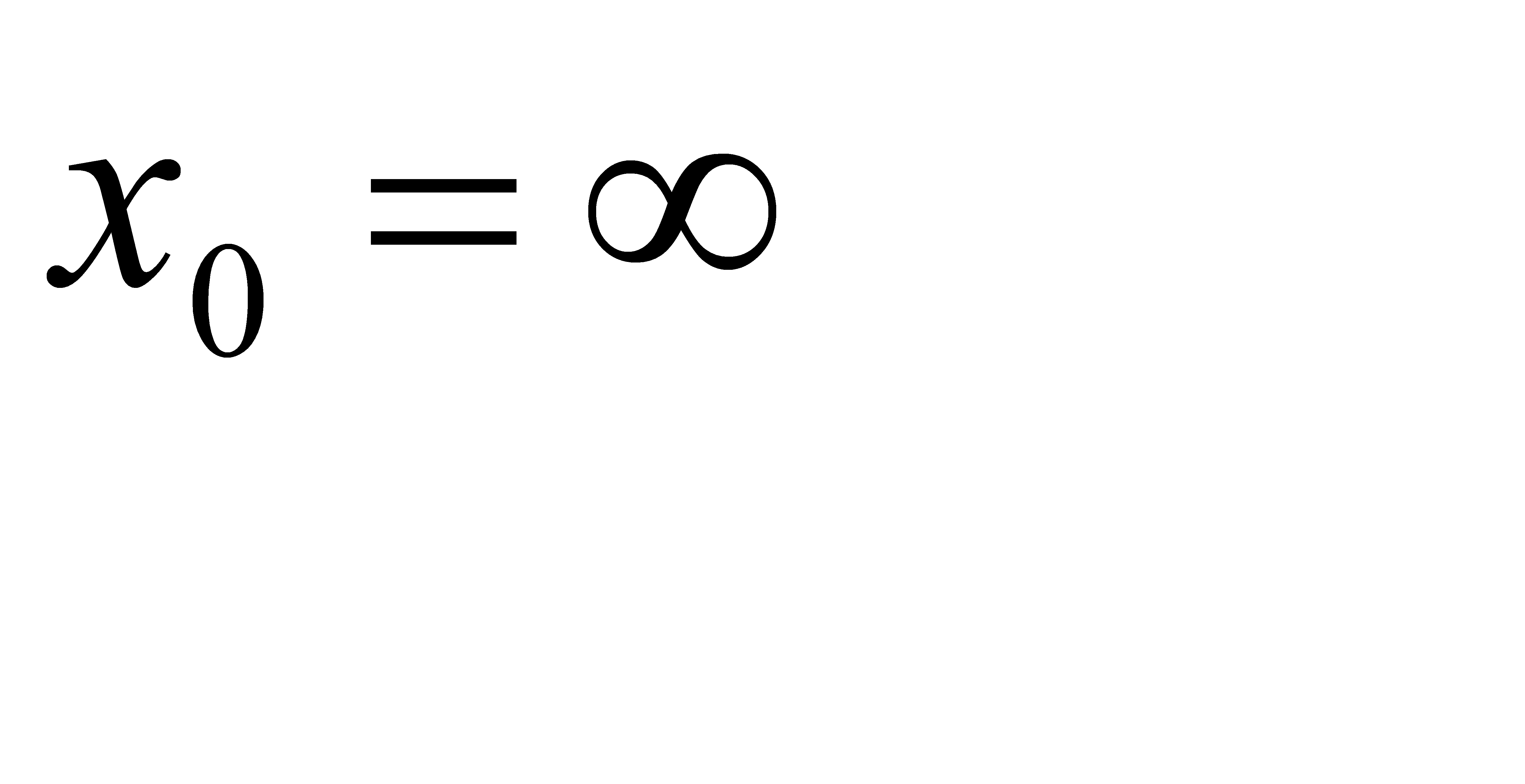 ;
;
2) 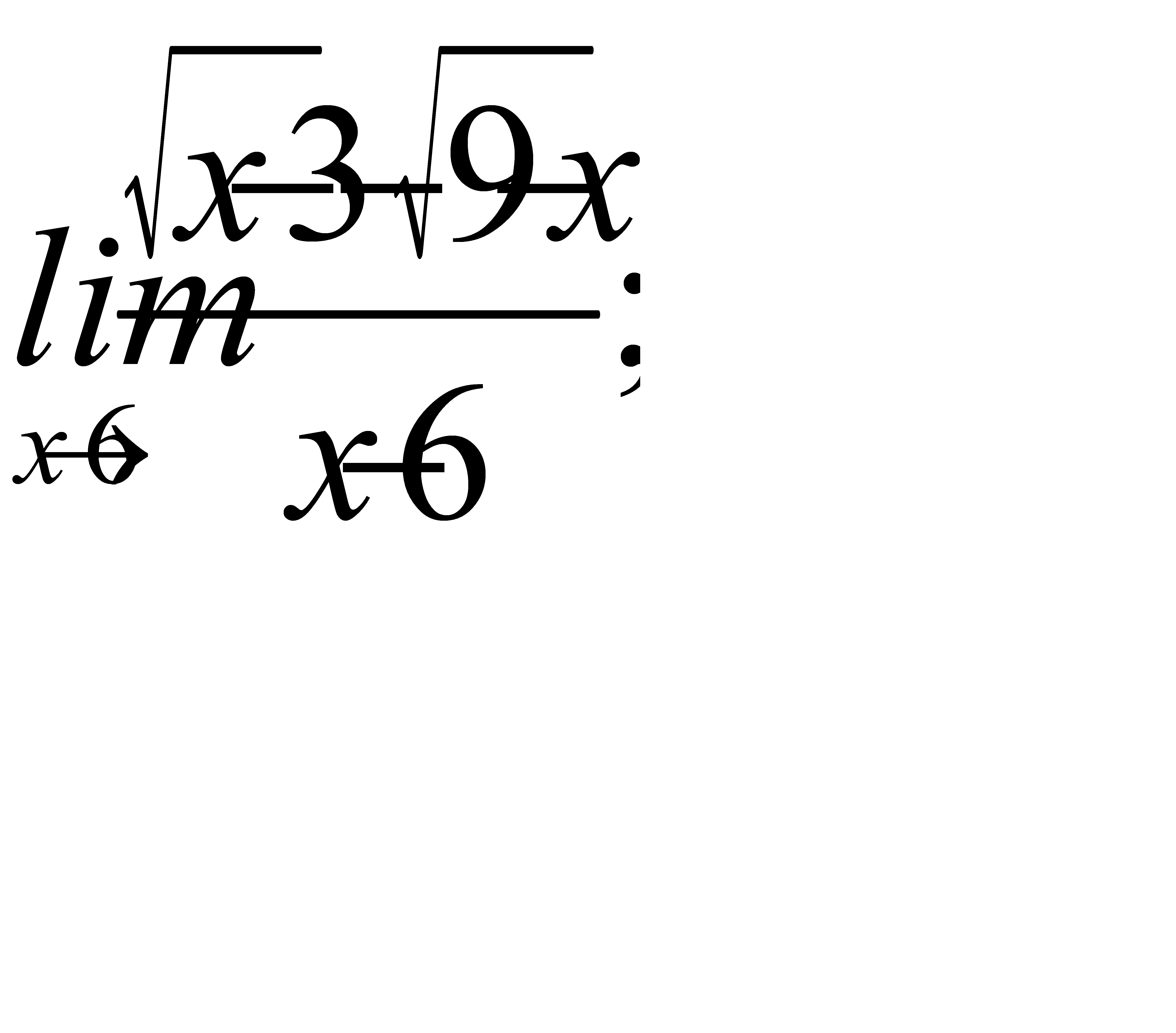 3)
3) 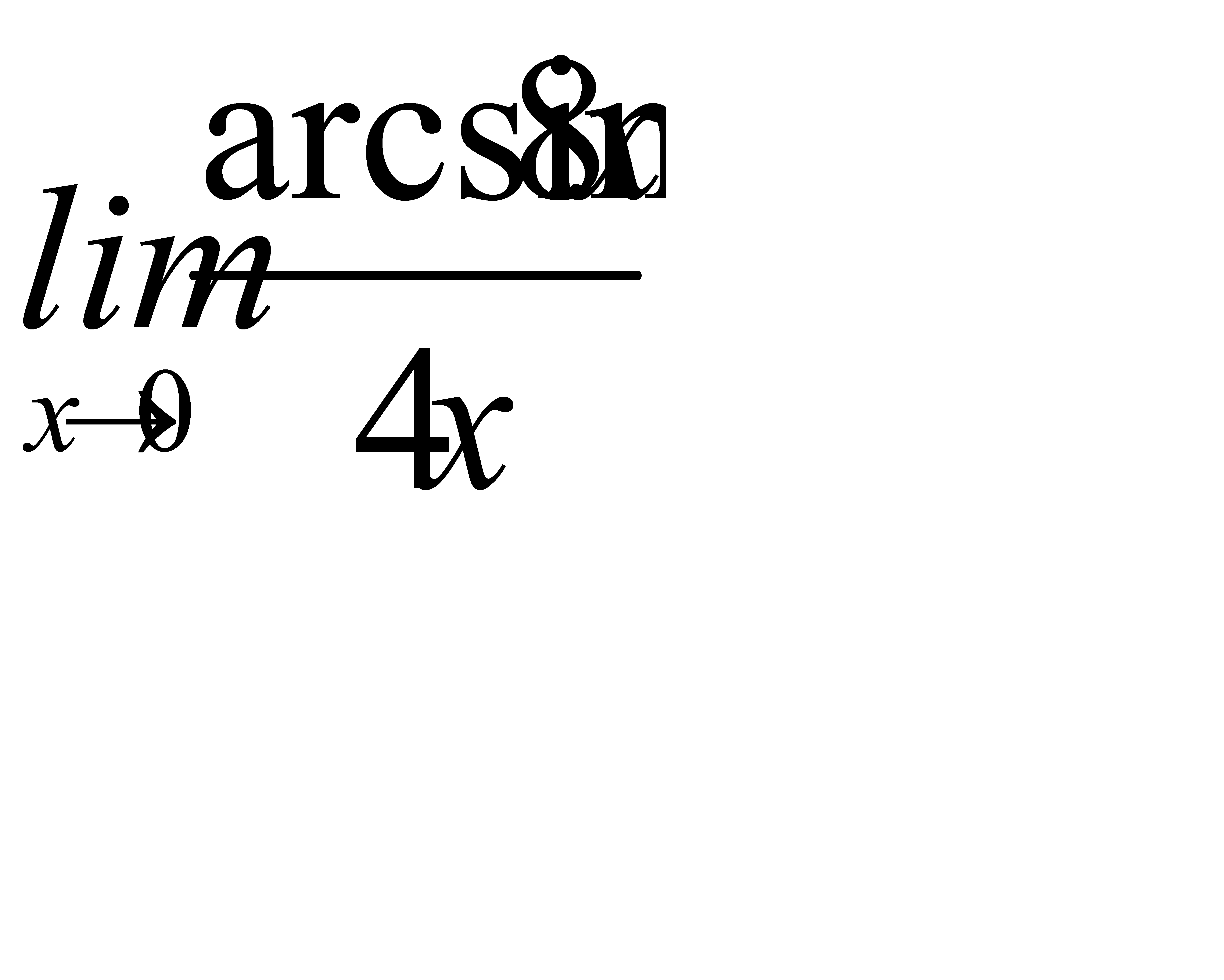 ;
;
4) 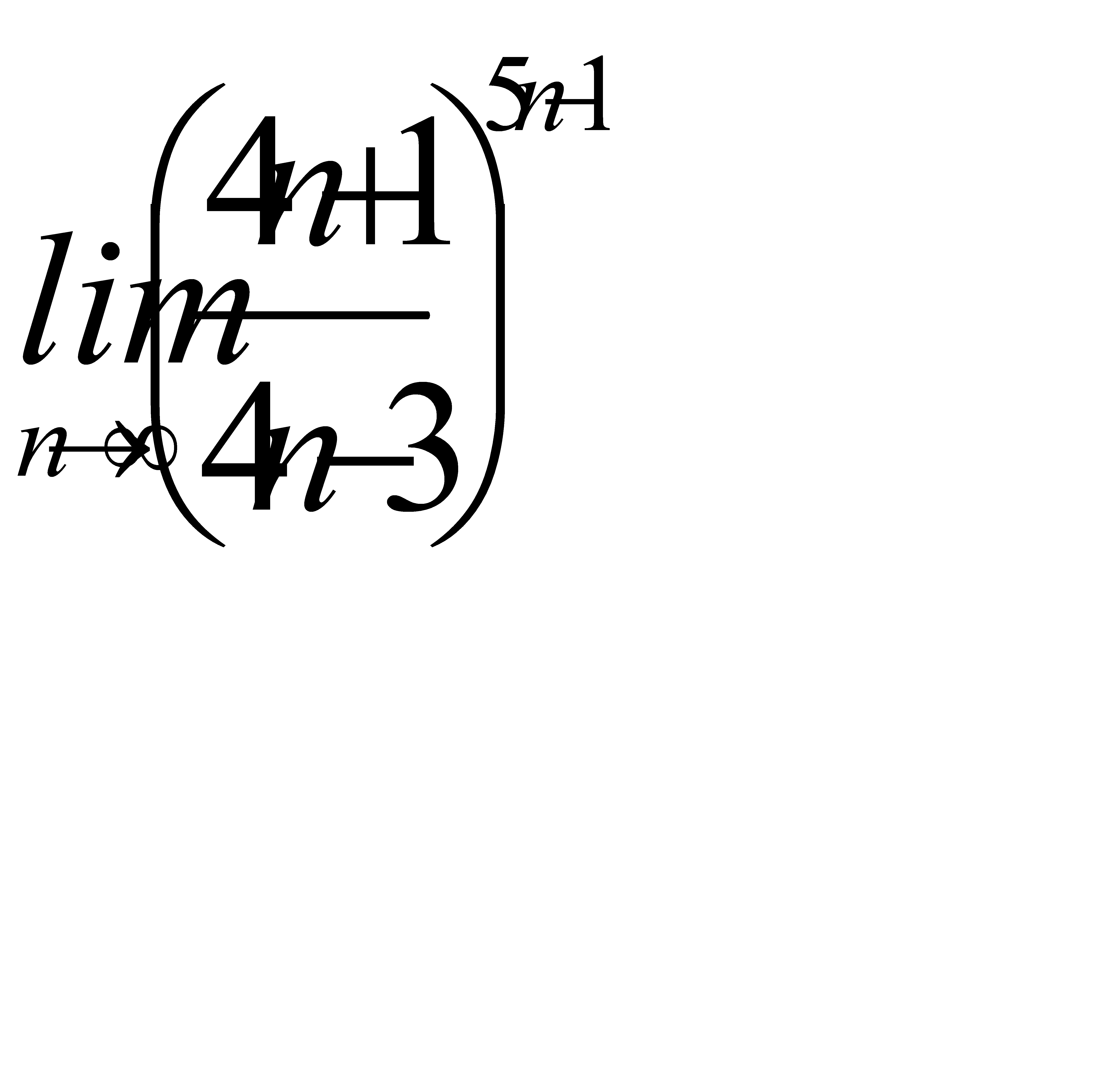
11-20. Найти производные заданных функций.
11. а) 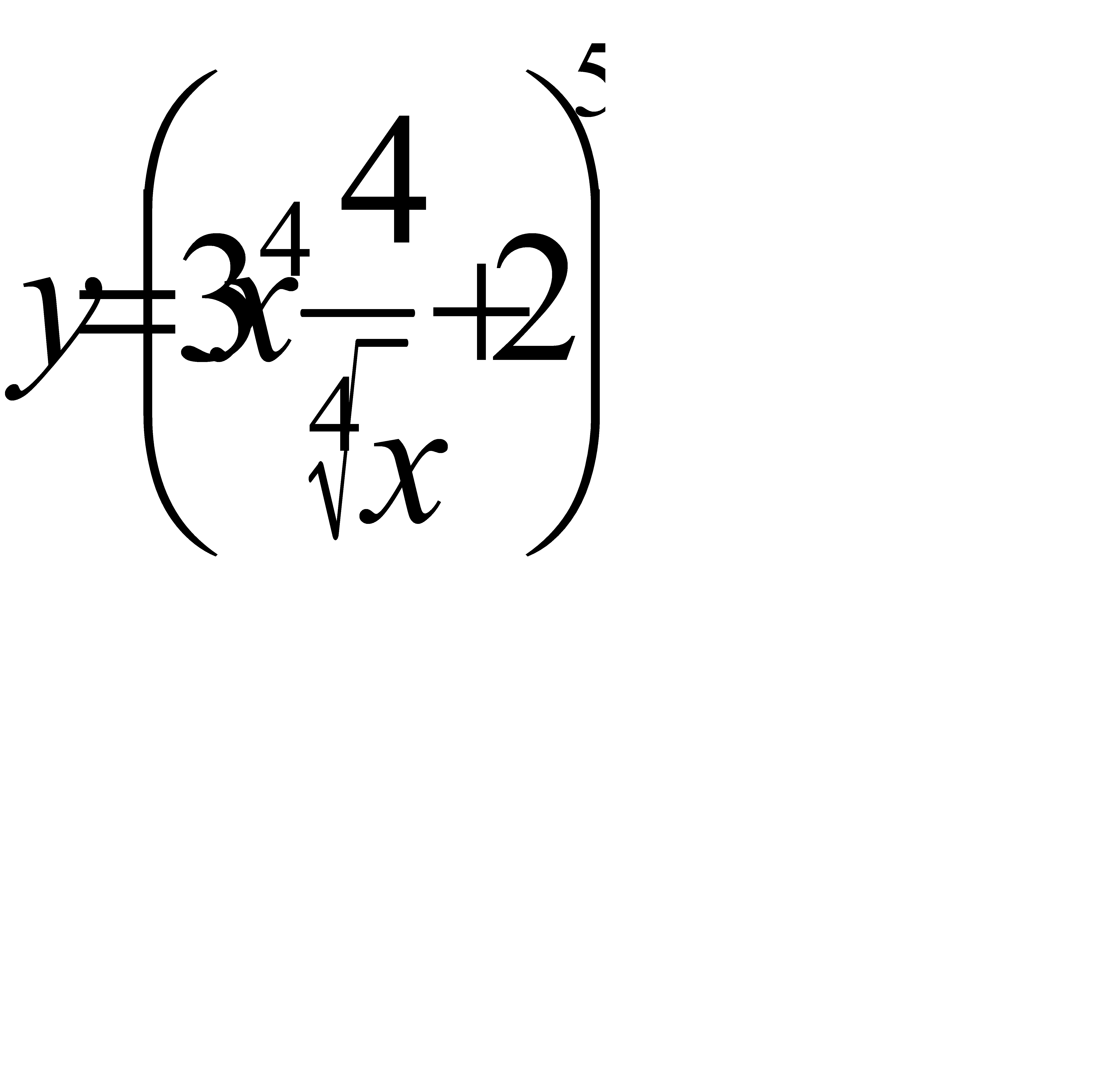 ; б)
; б) 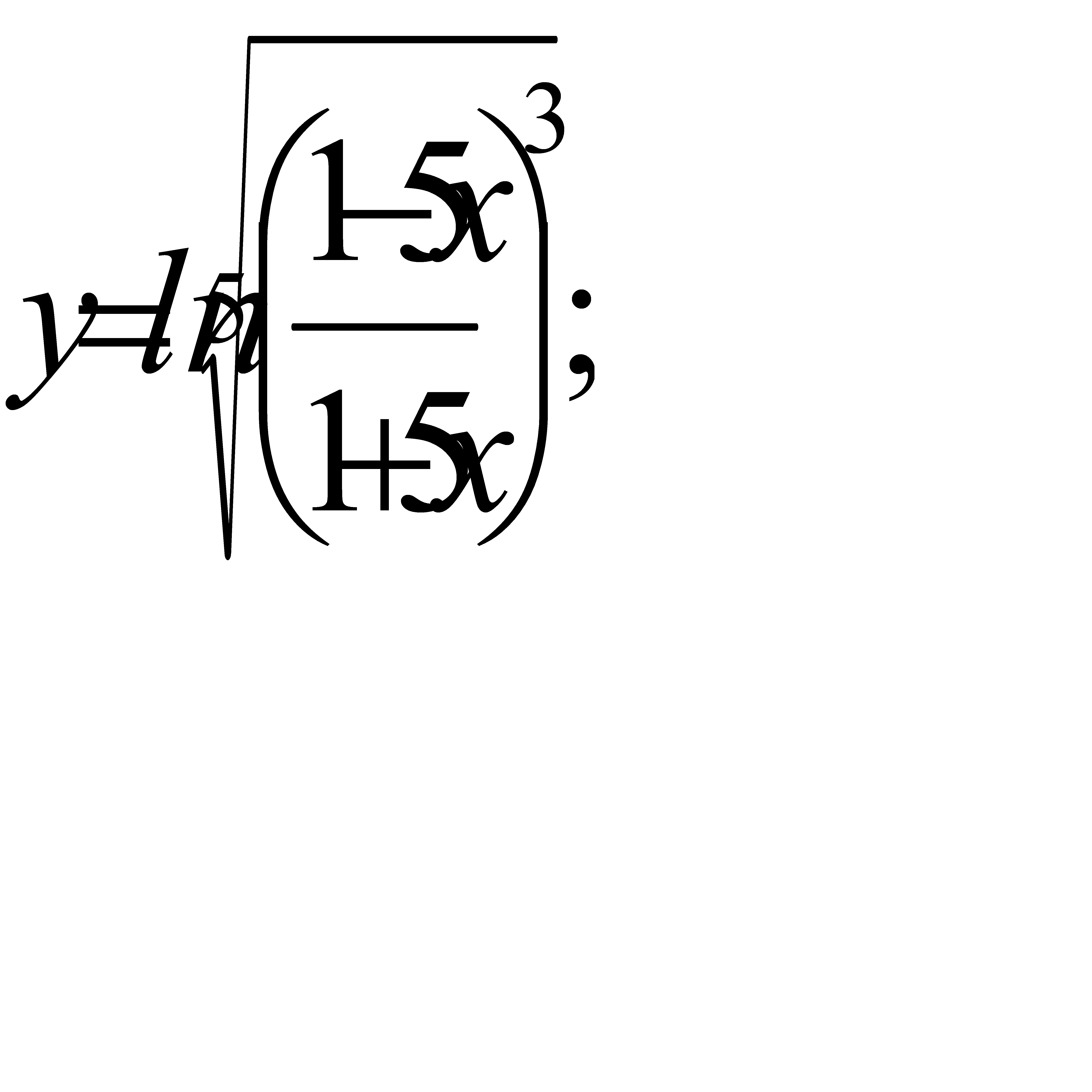
в) 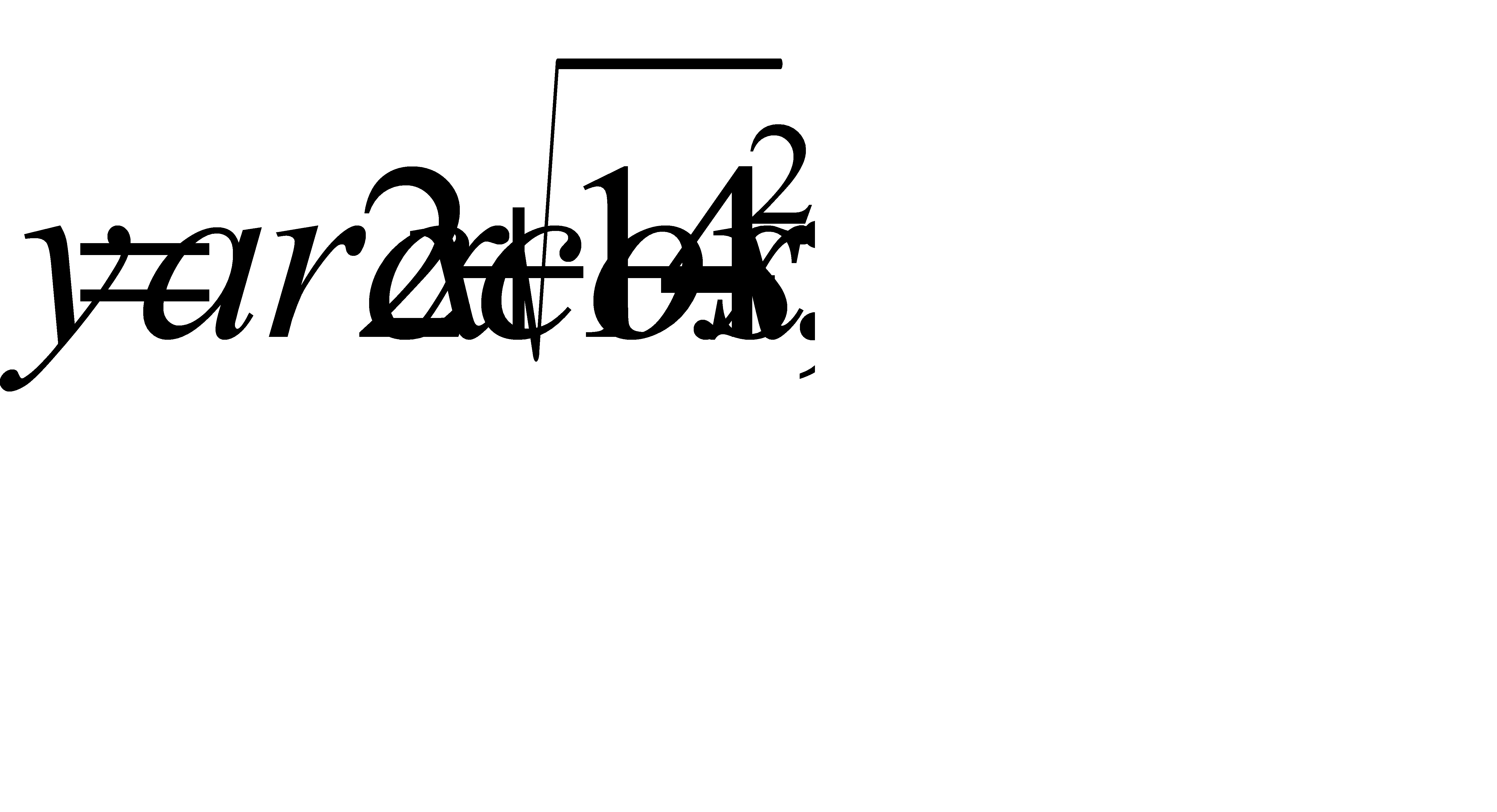 г)
г)  .
.
12. а) 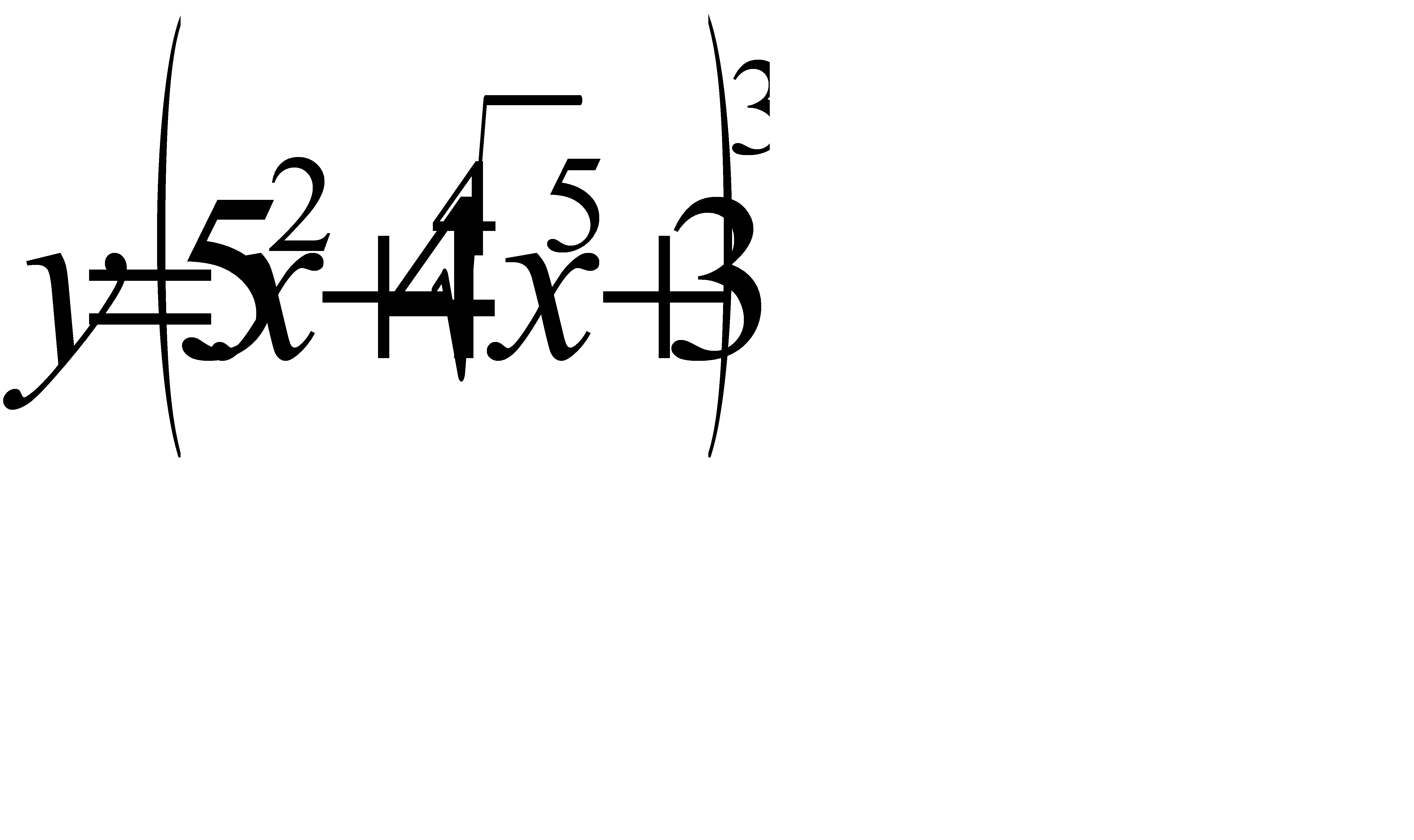 ; б)
; б) 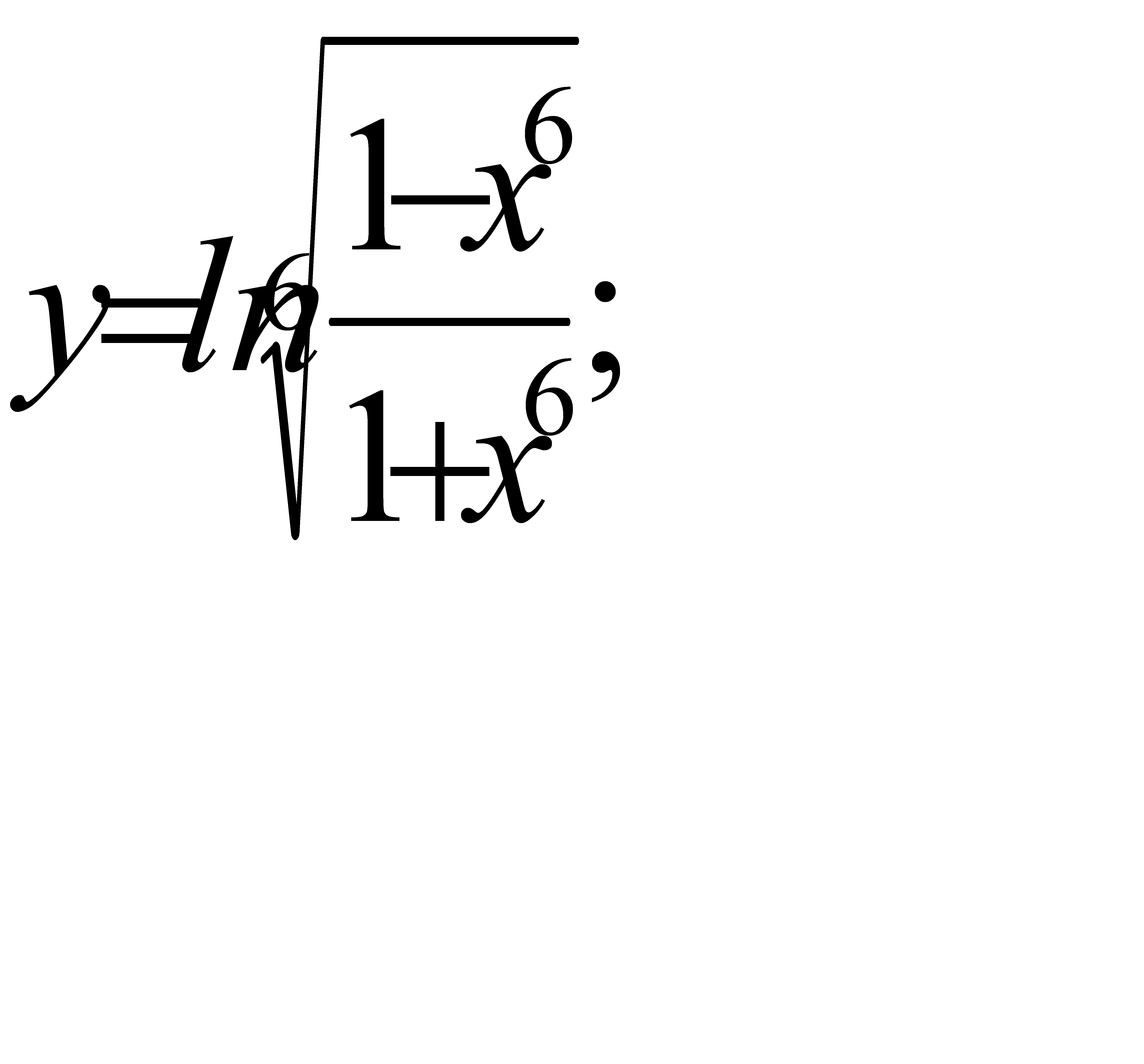
в) 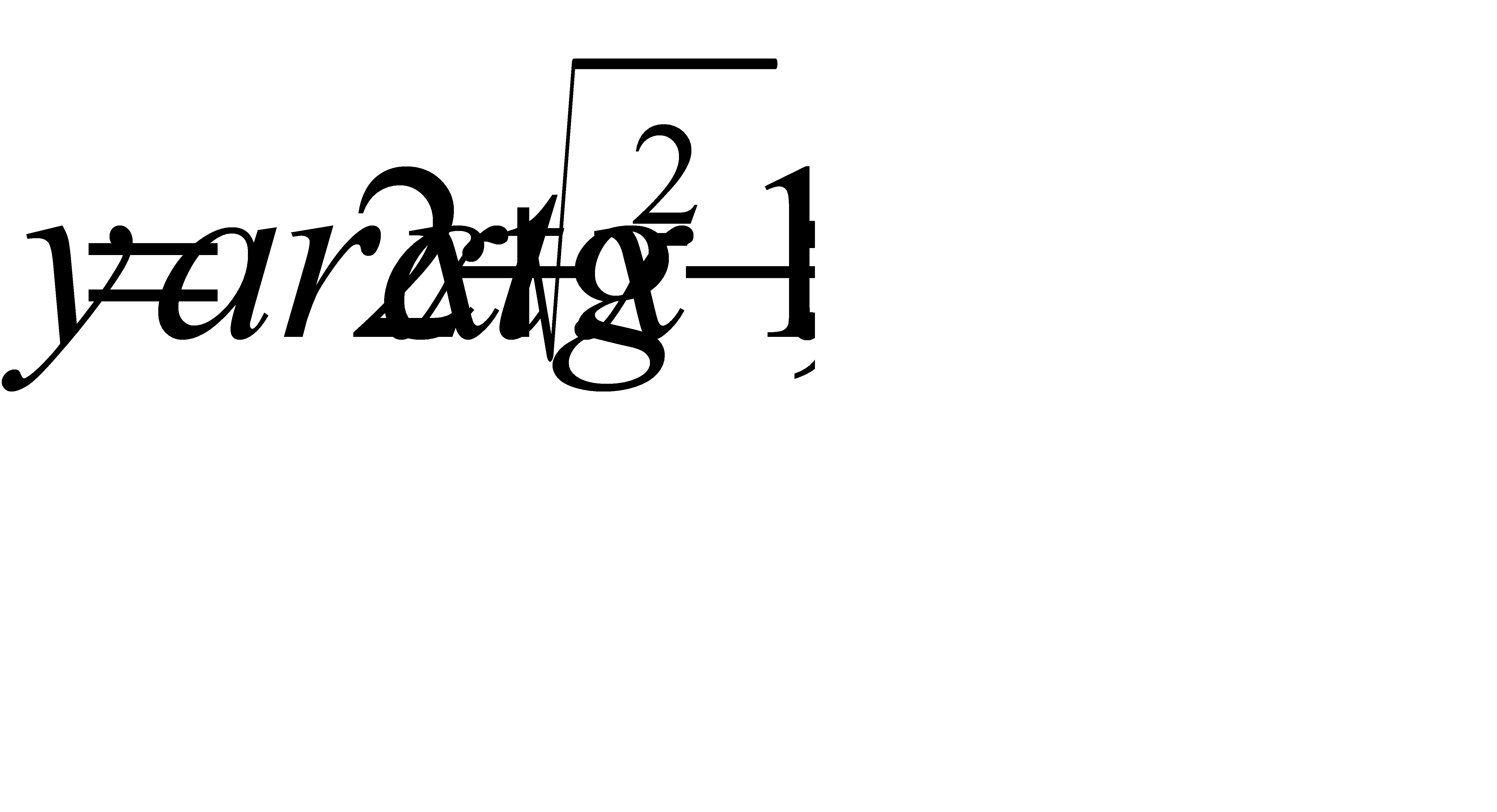 г)
г) 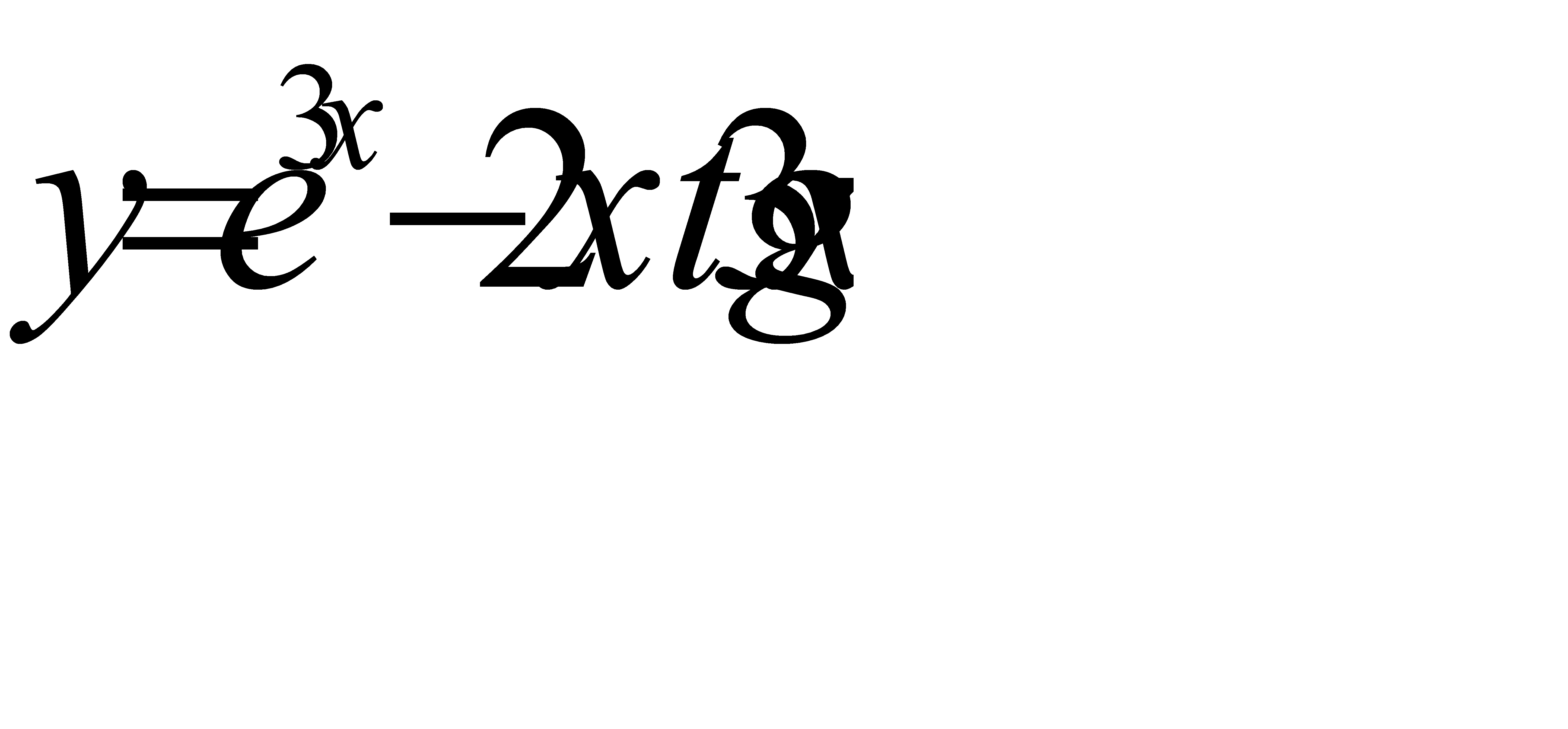 .
.
13. а) 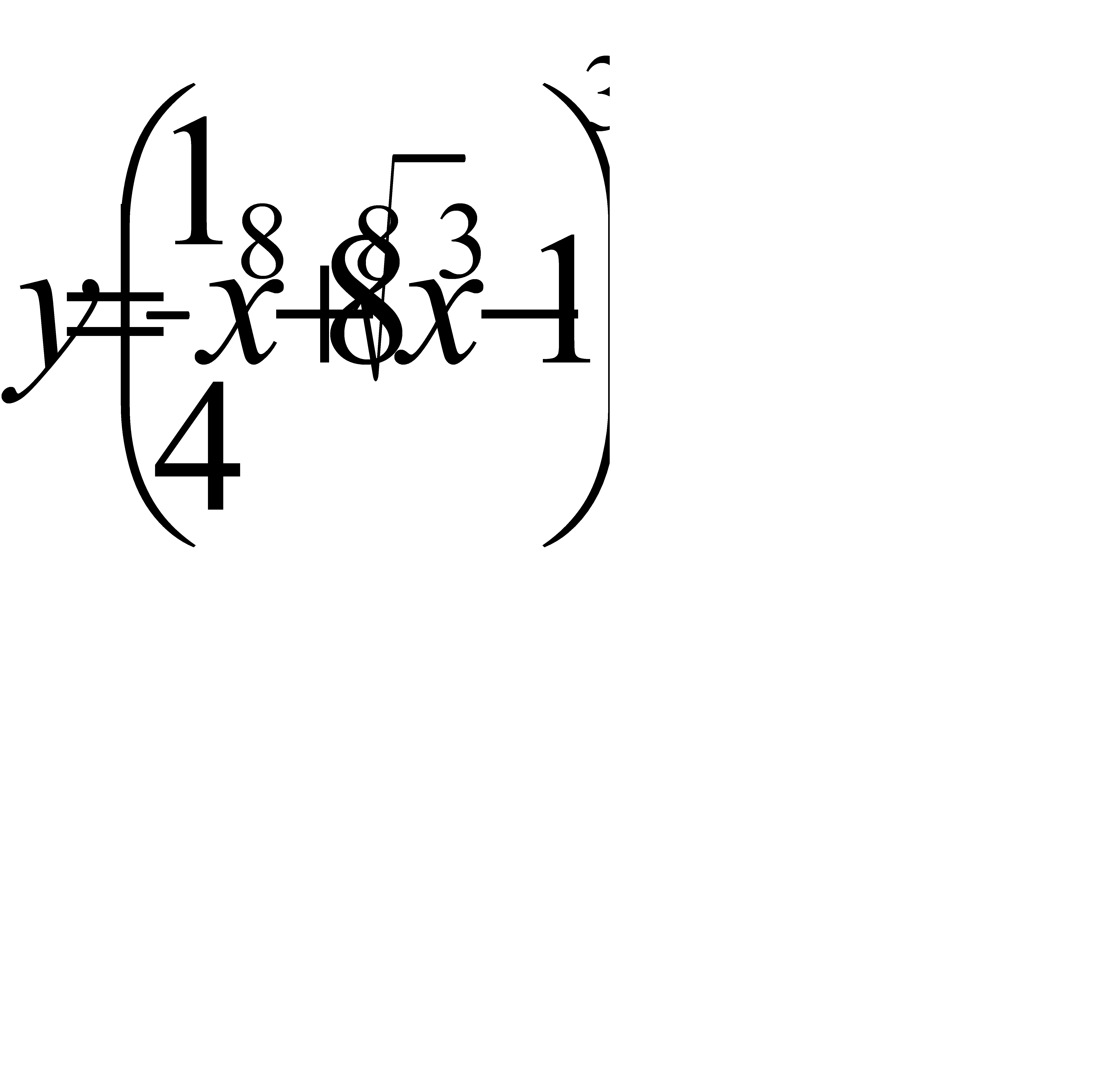 ; б)
; б) 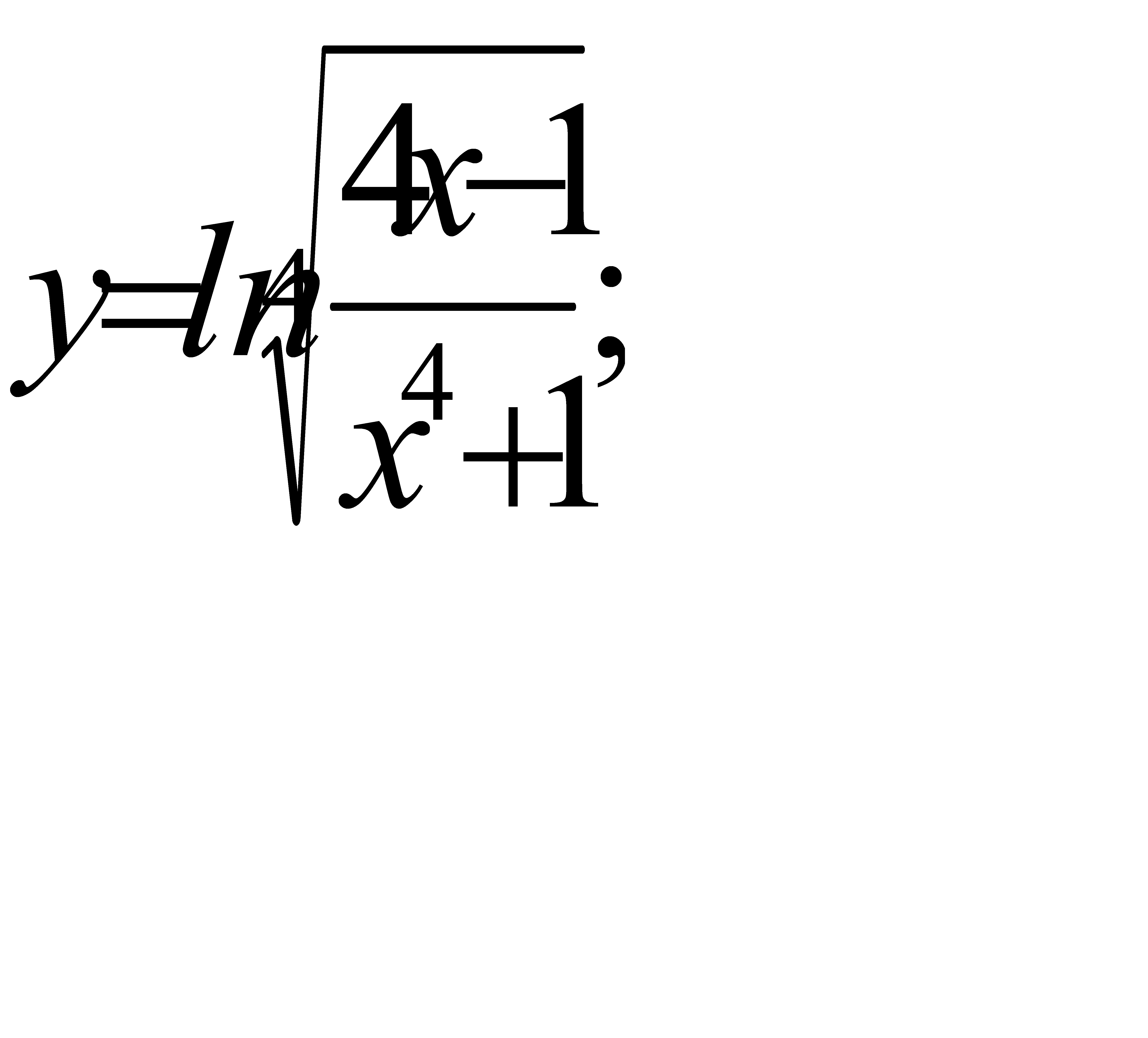
в) 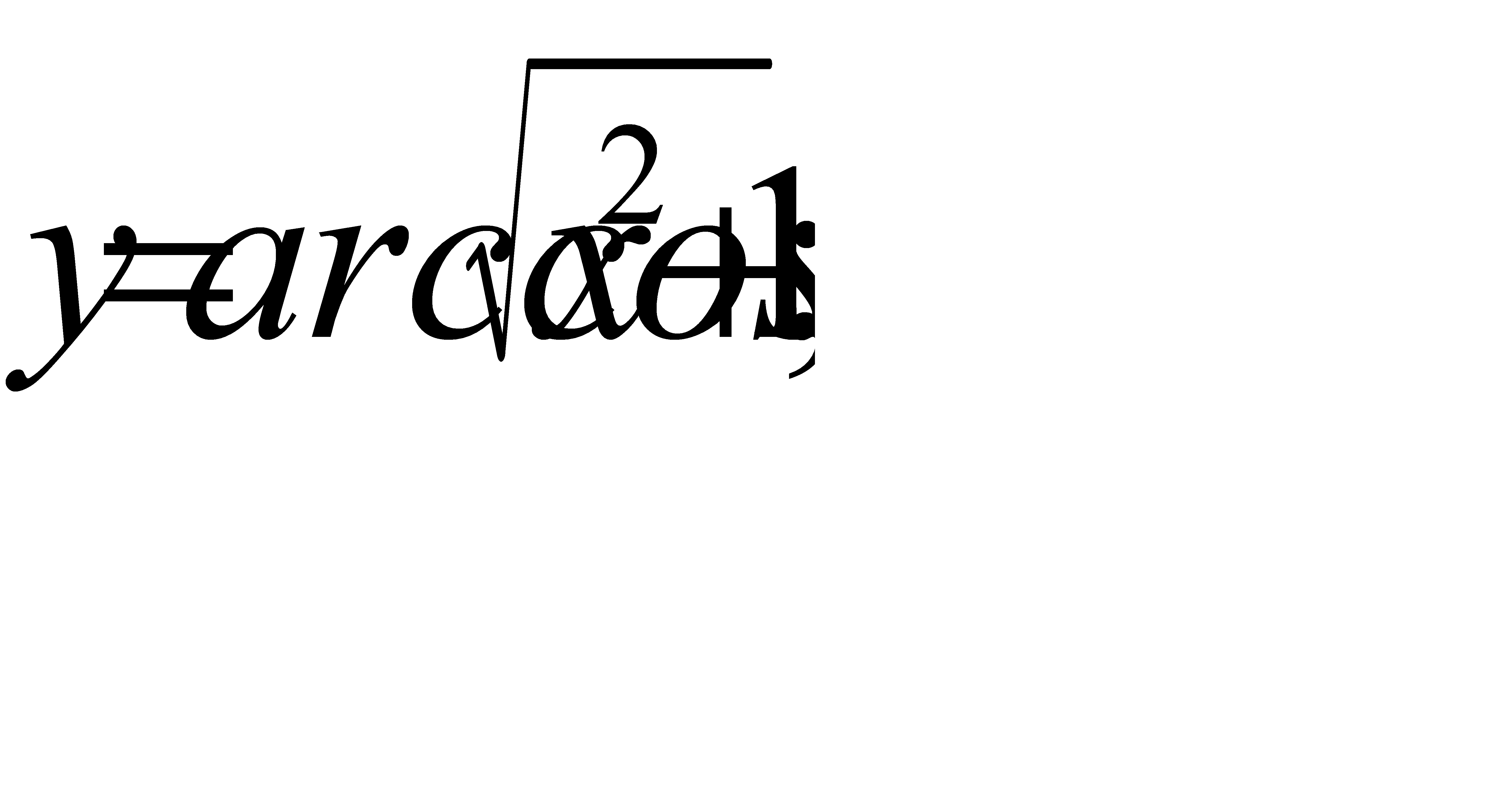 г)
г) 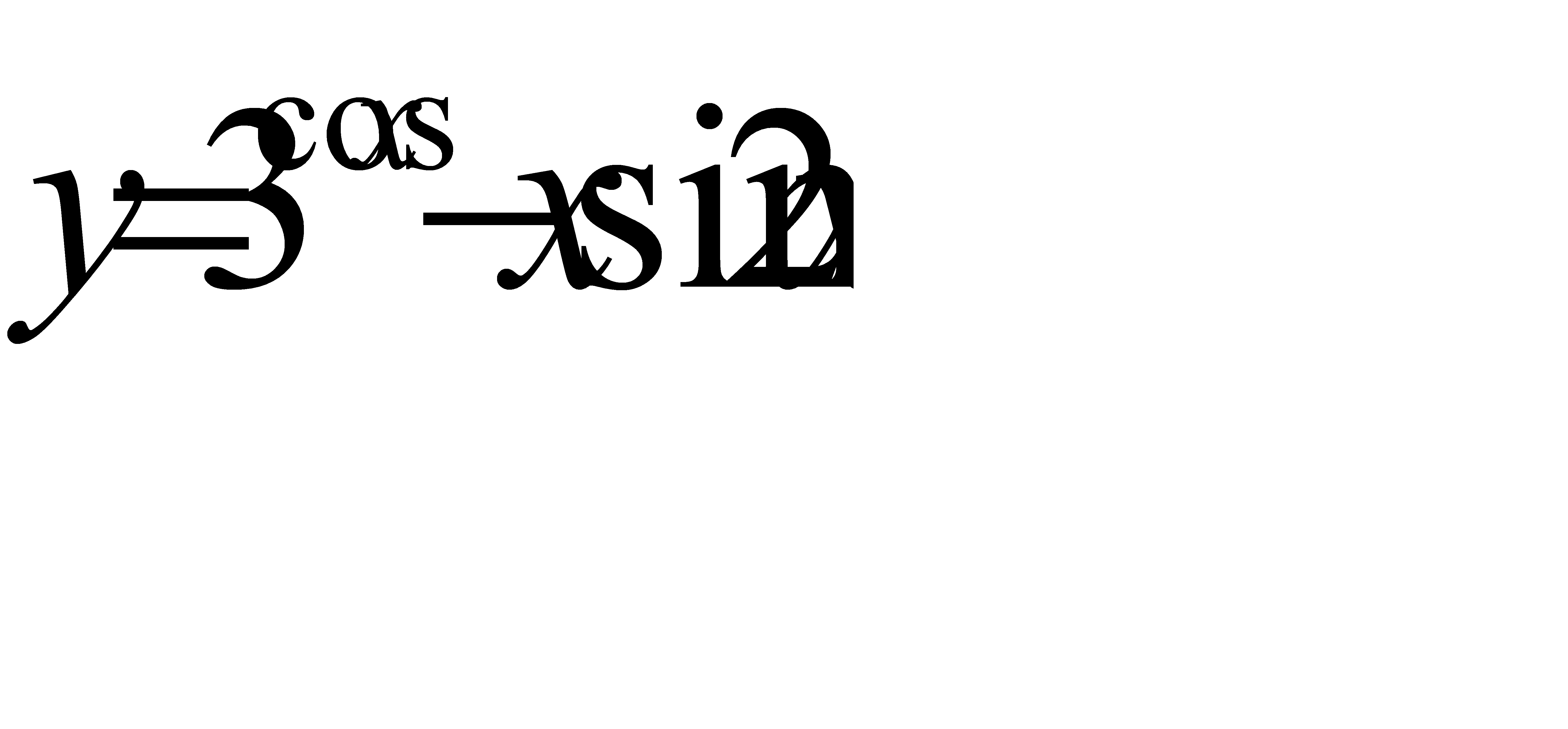 .
.
14. а) 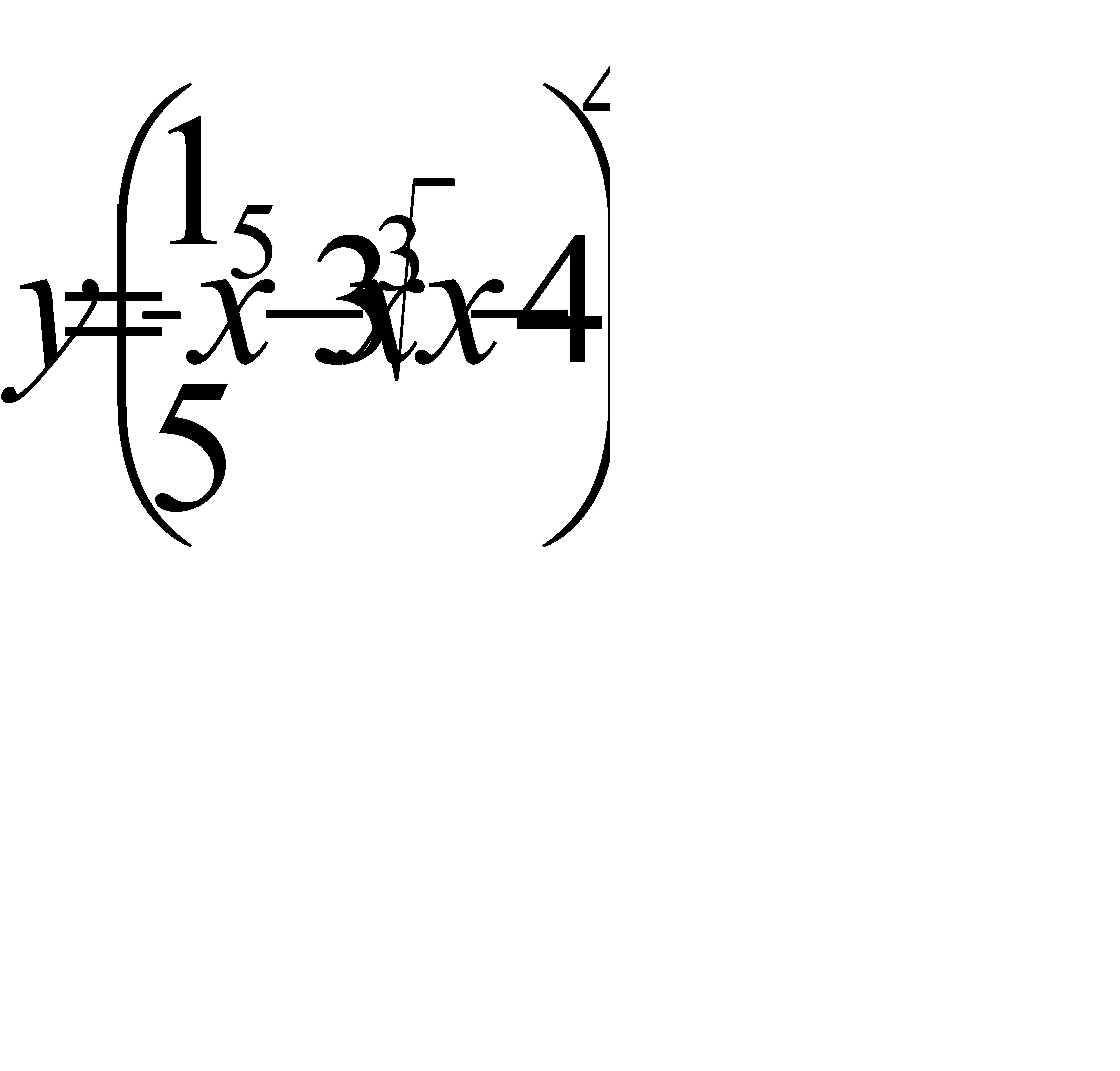 ; б)
; б) 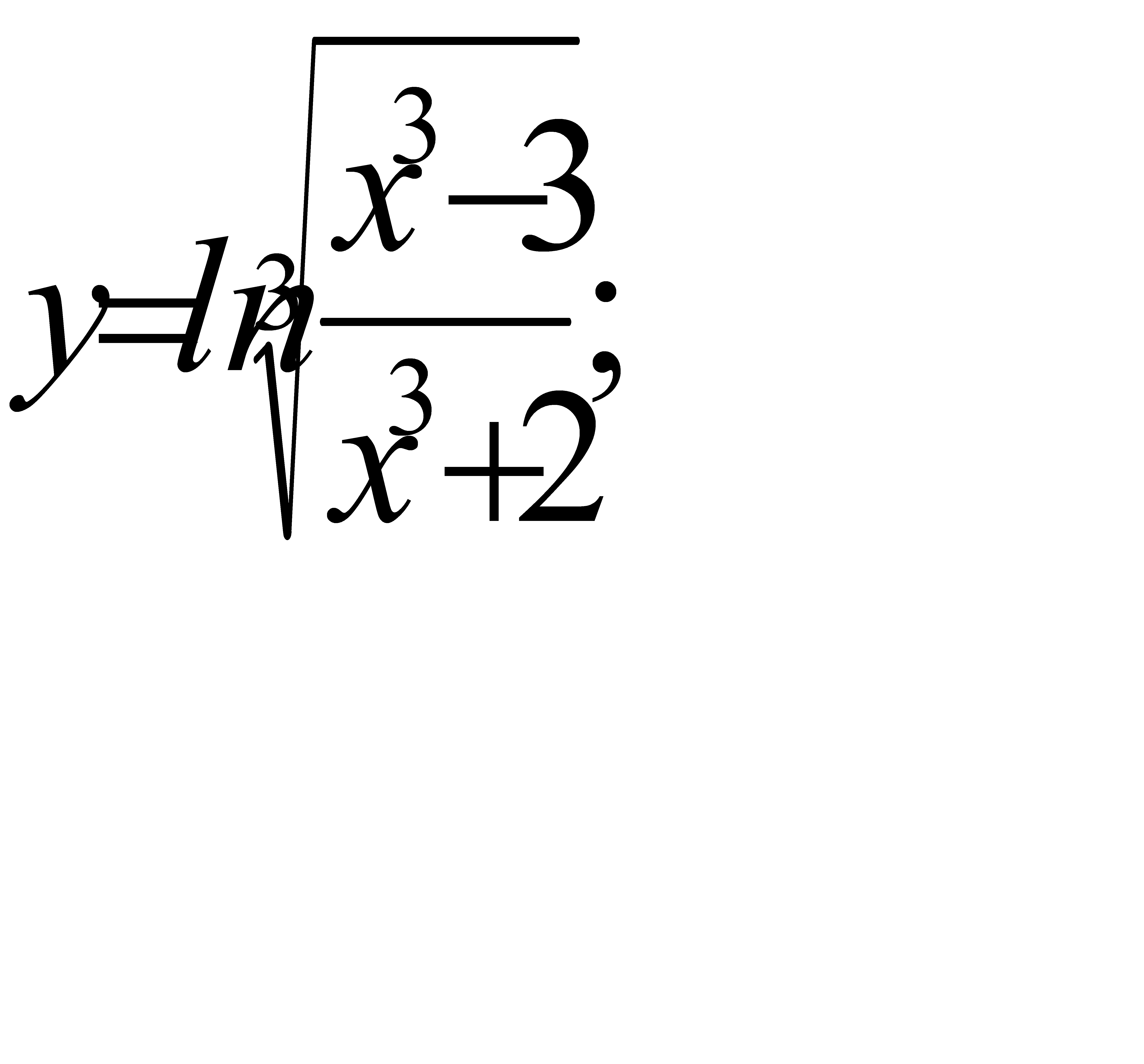
в) 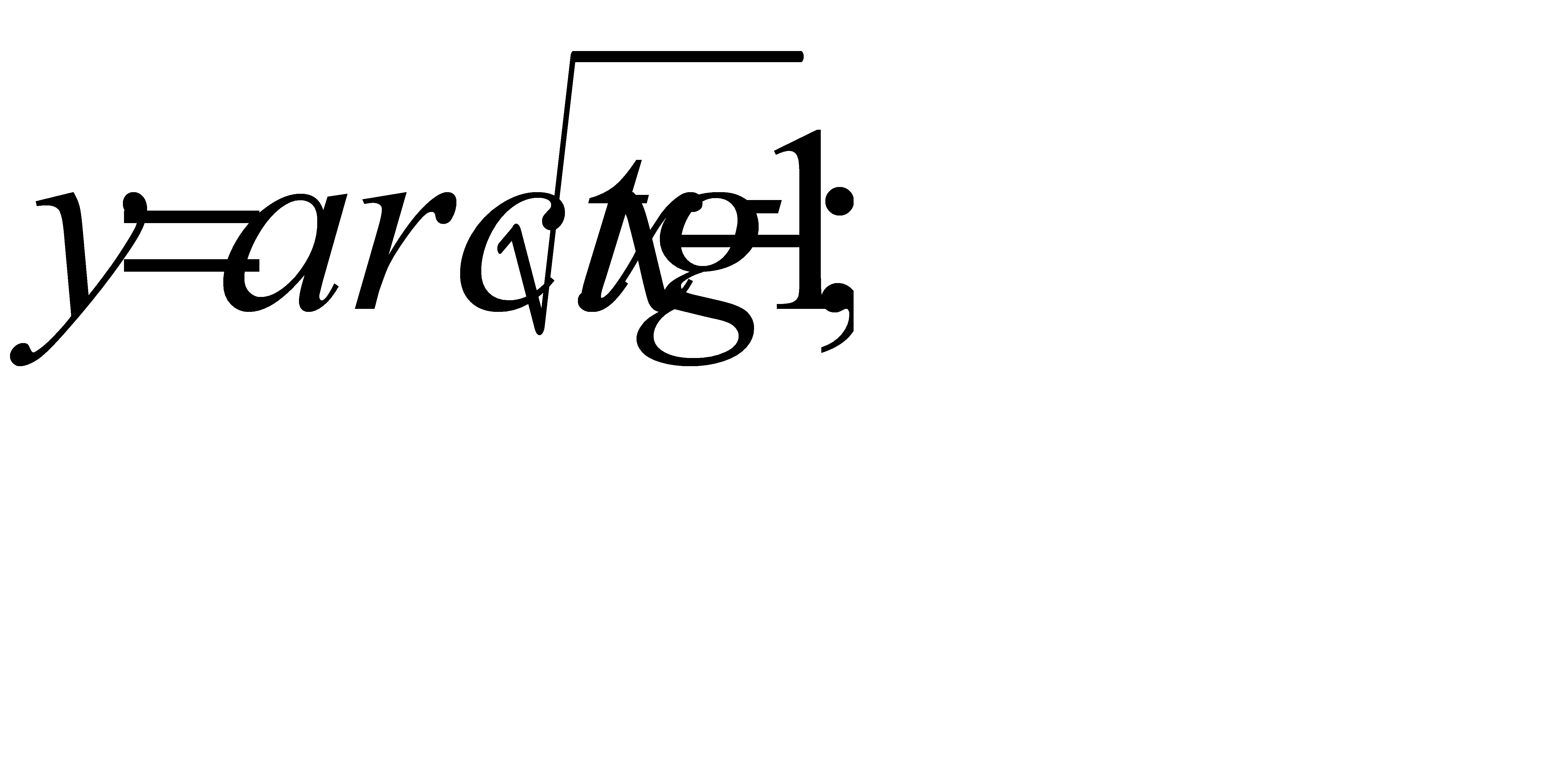 г)
г) 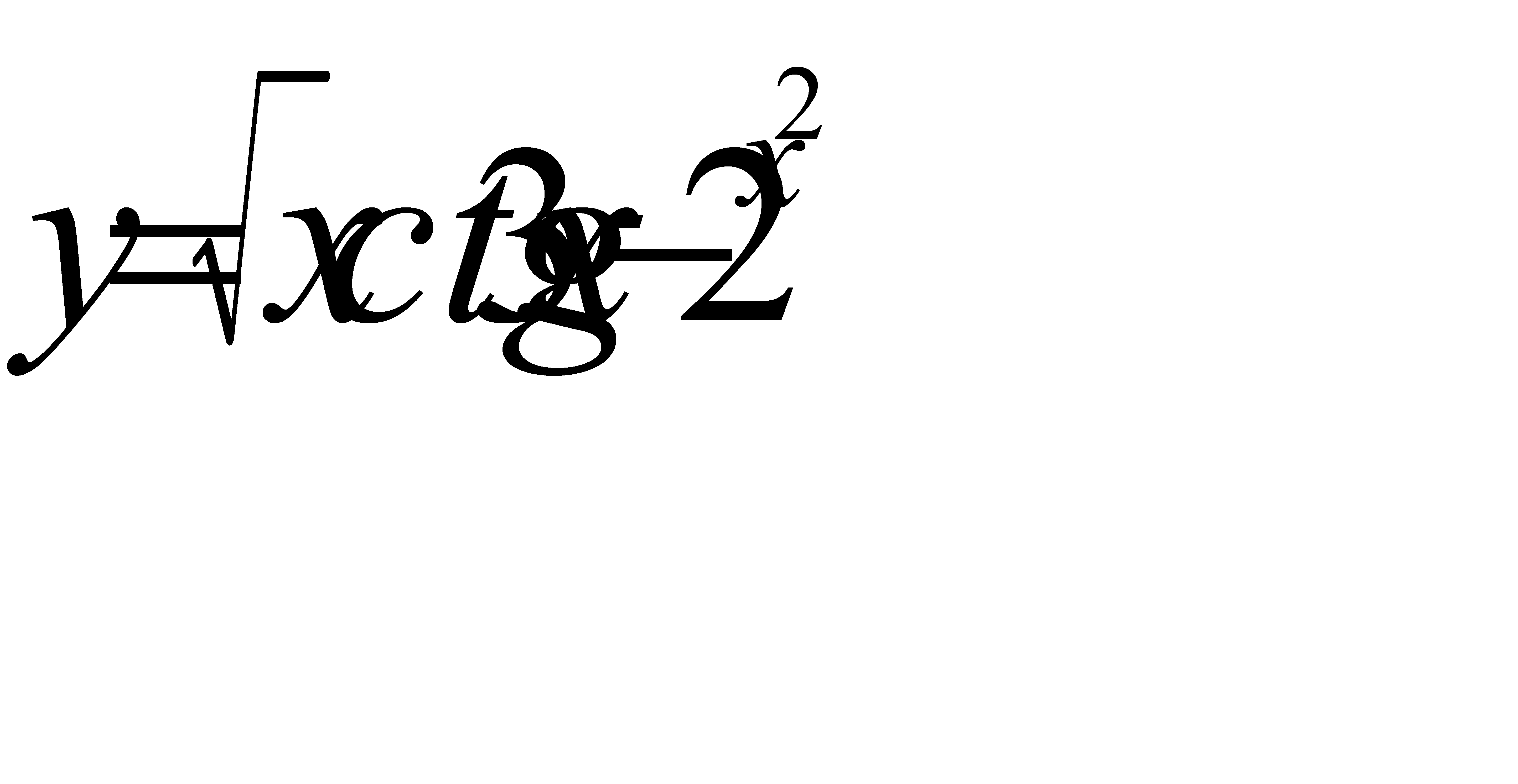 .
.
- а)
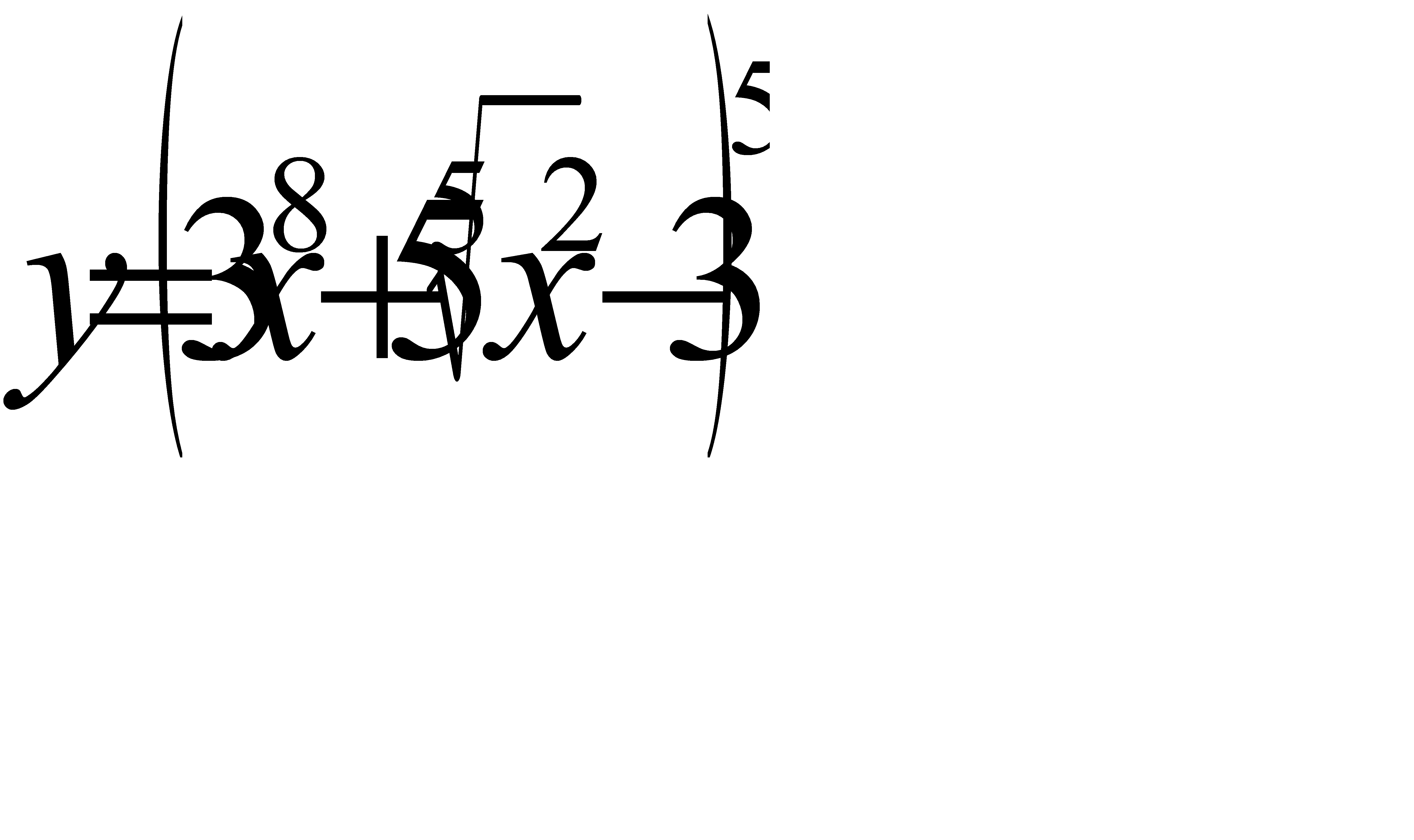 ; б)
; б) 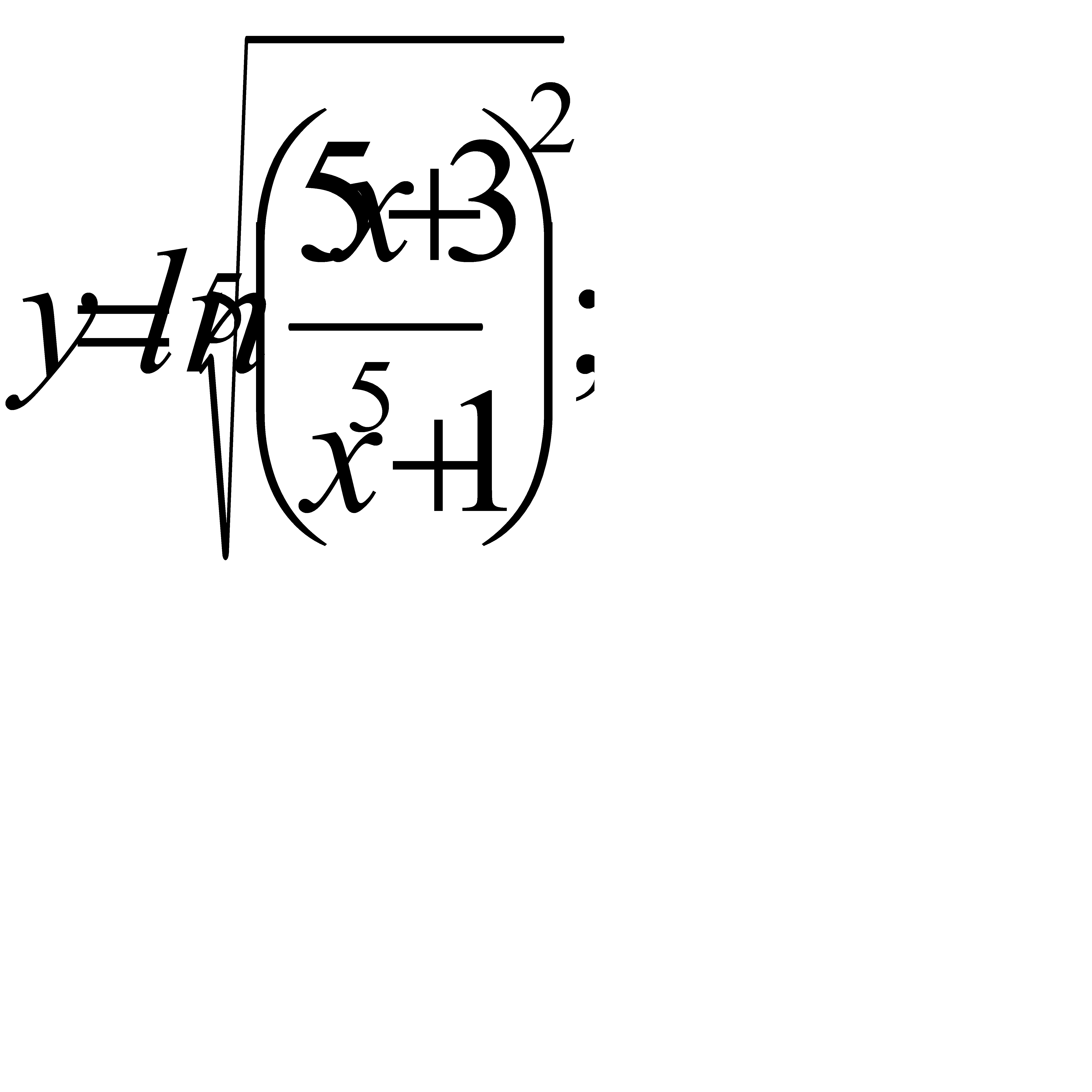
в) 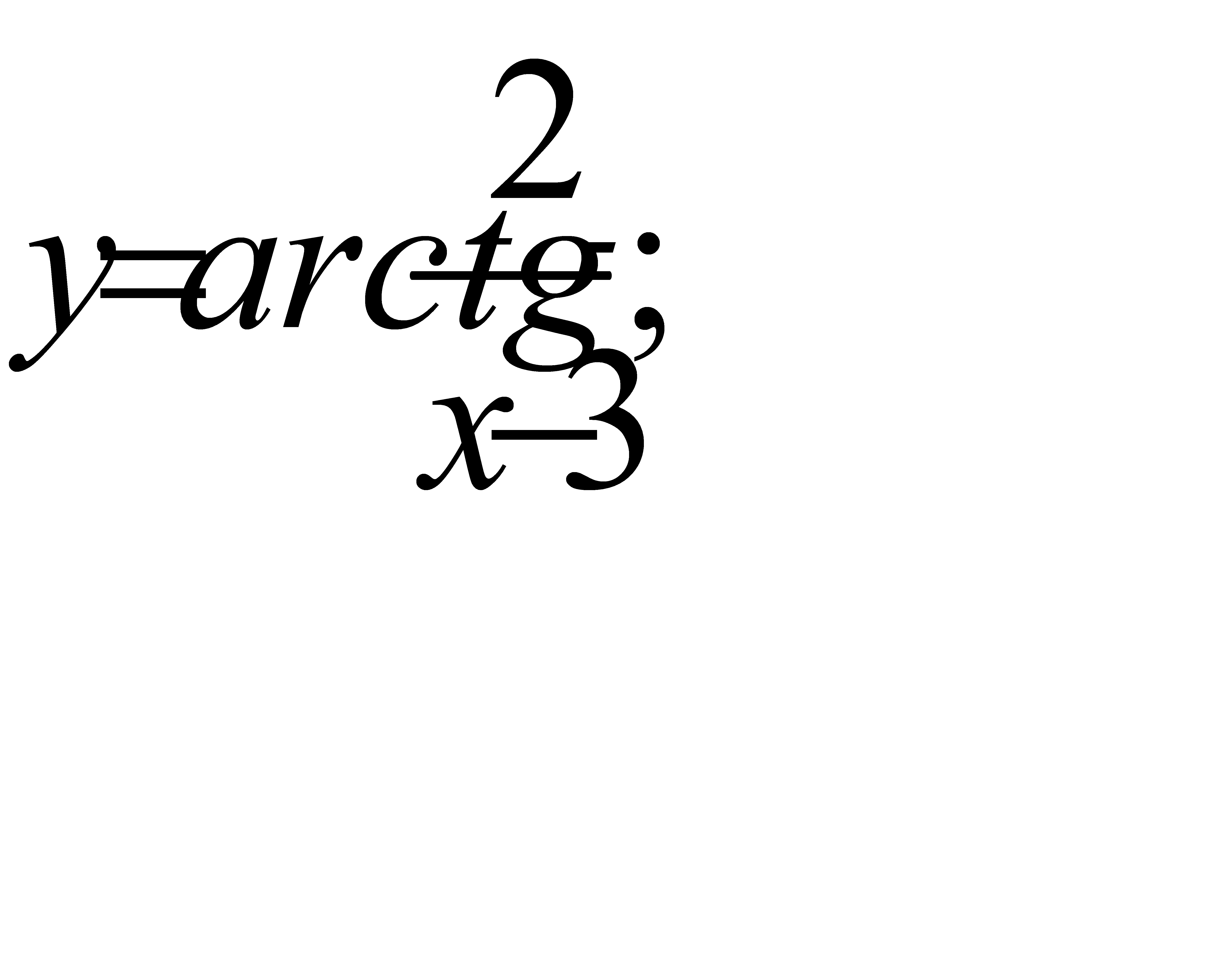 г)
г) 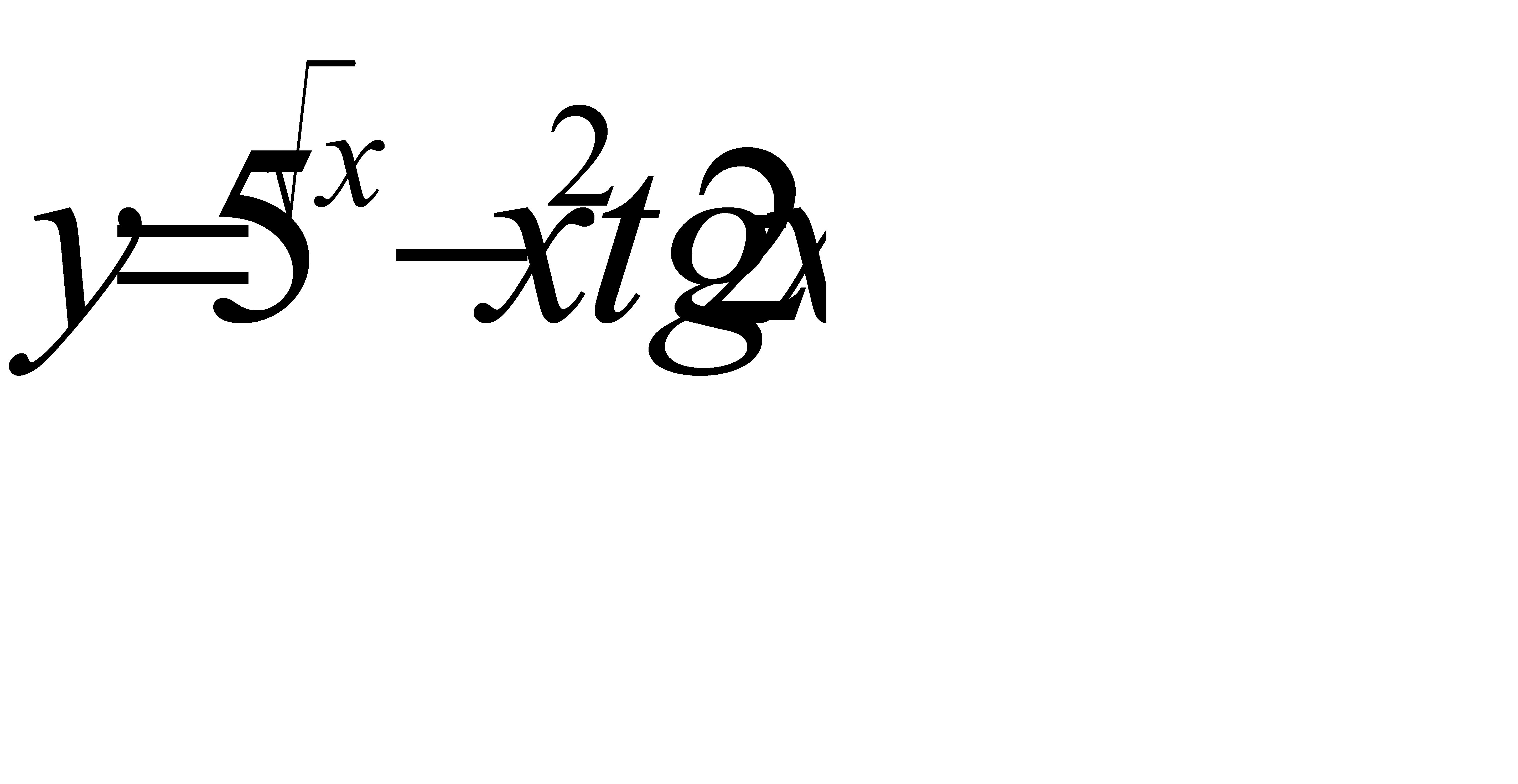 .
.
16. а) 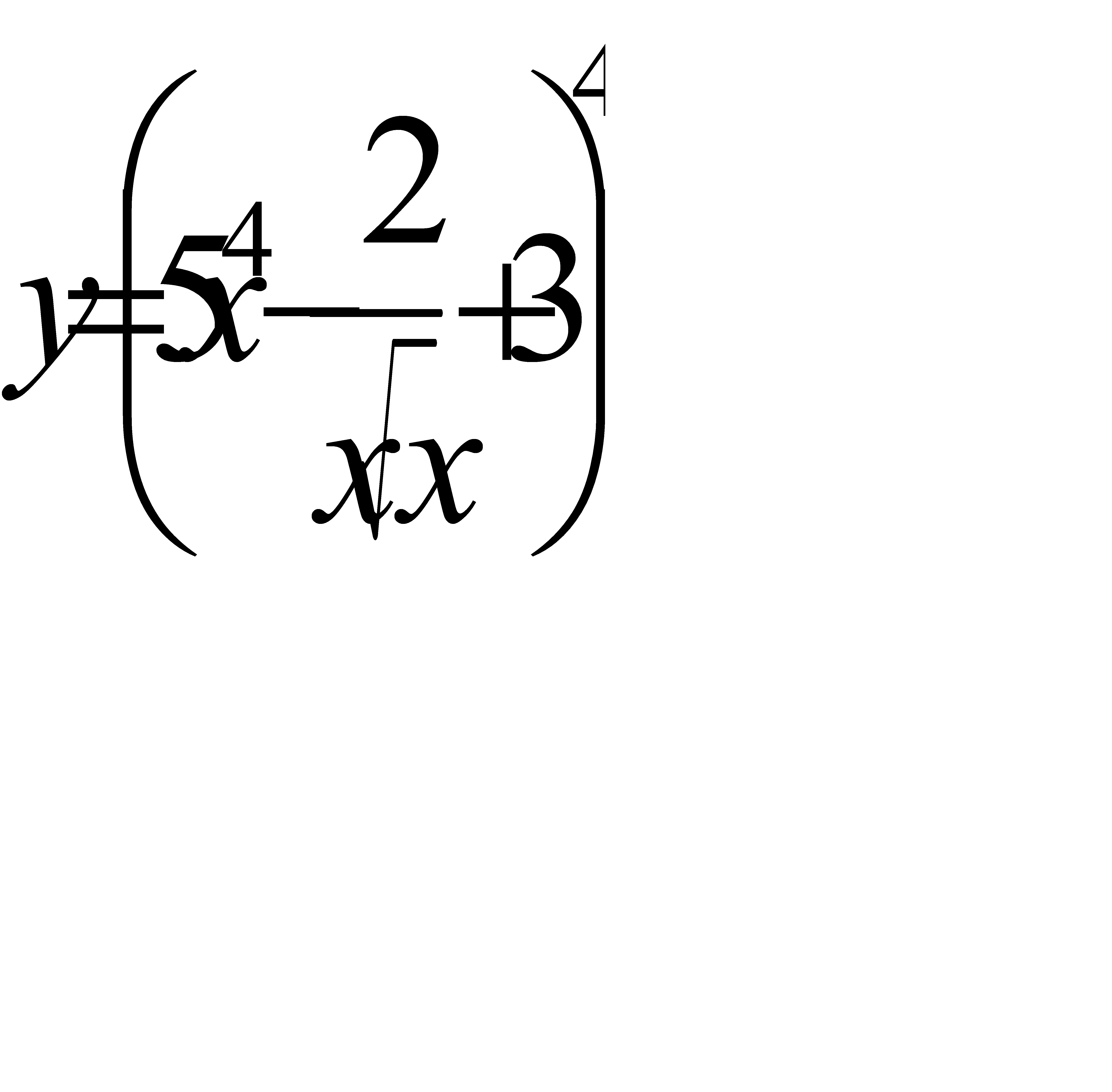 ; б)
; б) 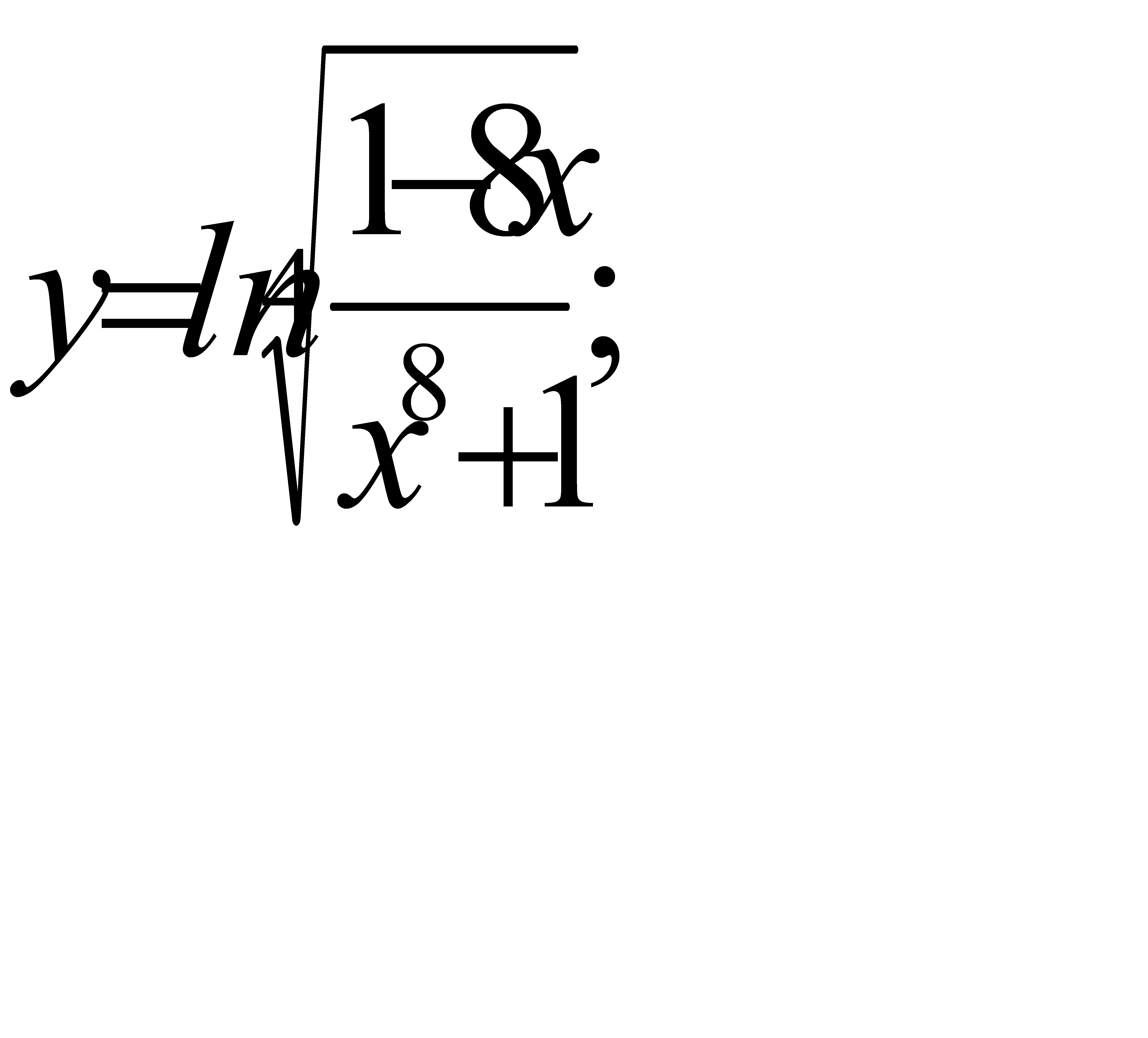
в) 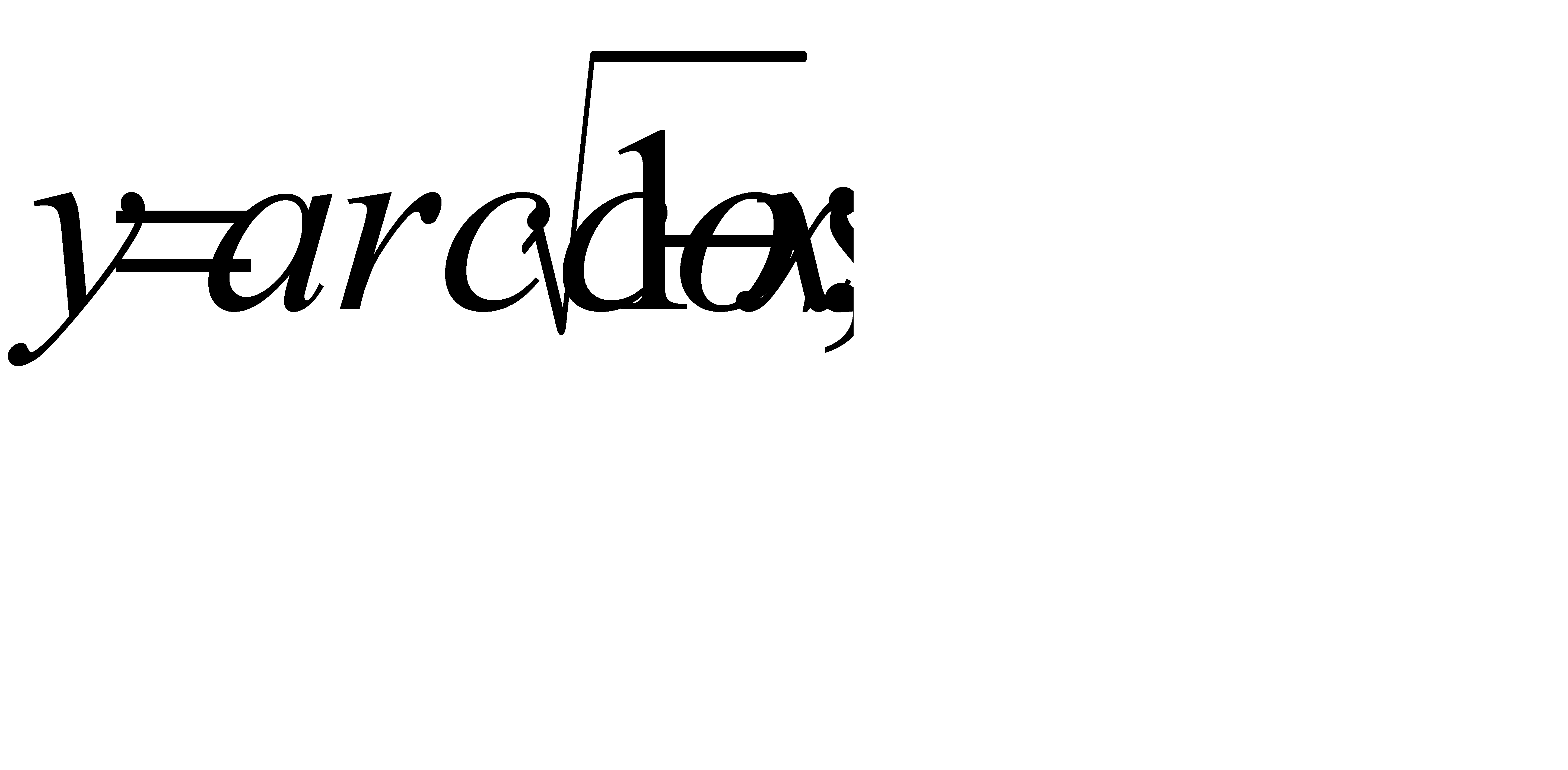 г)
г) 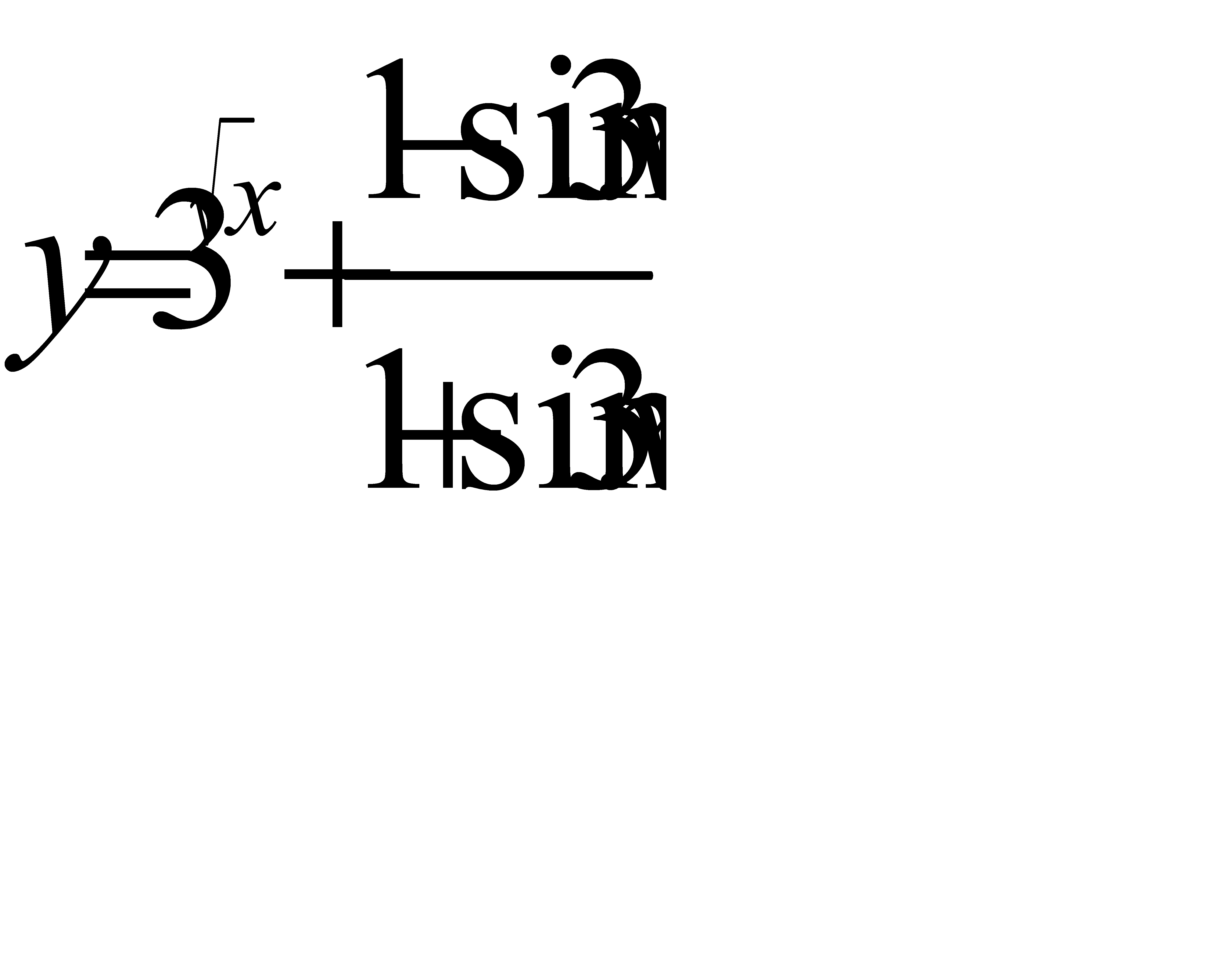 .
.
17. а) 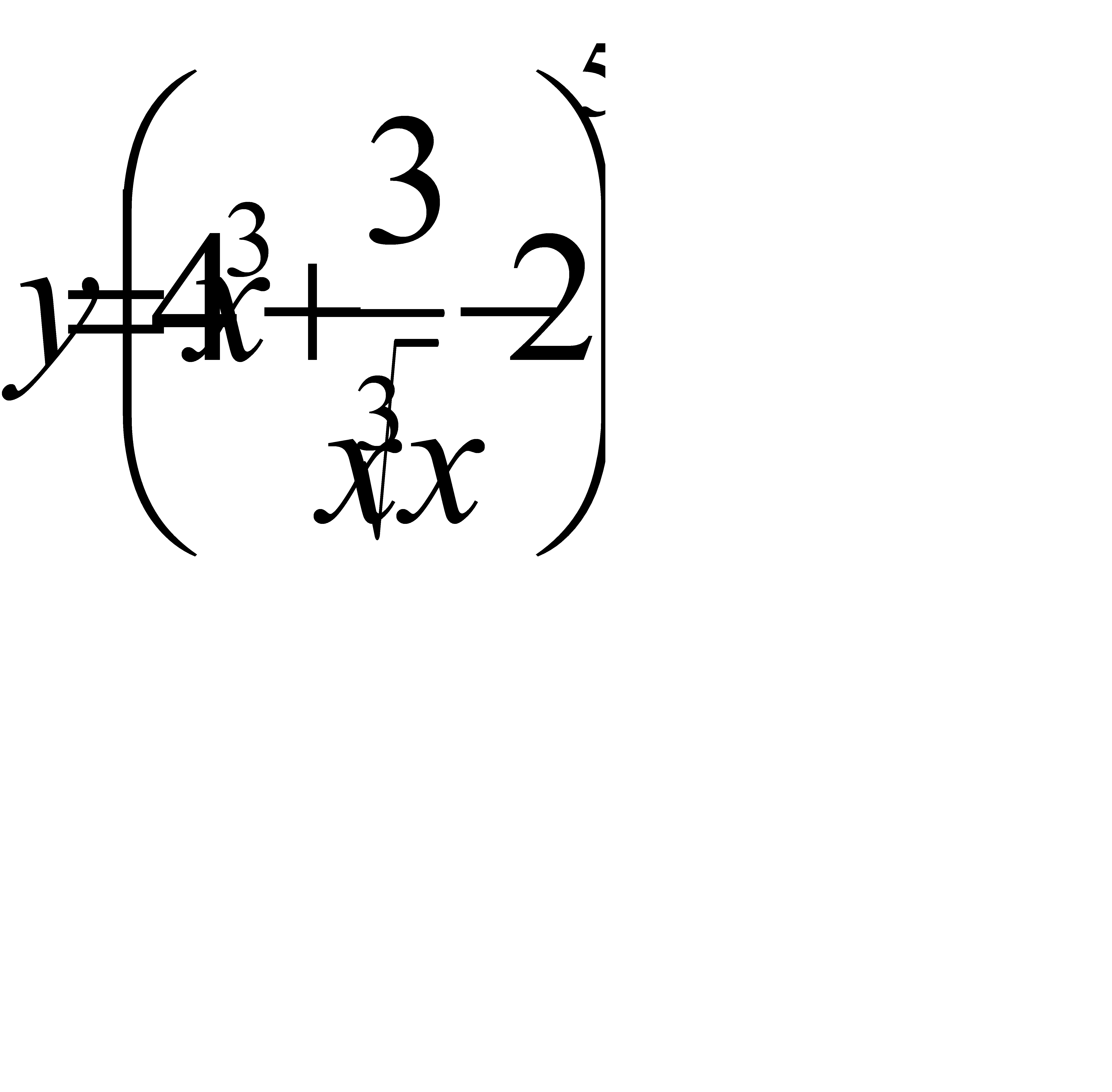 ; б)
; б) 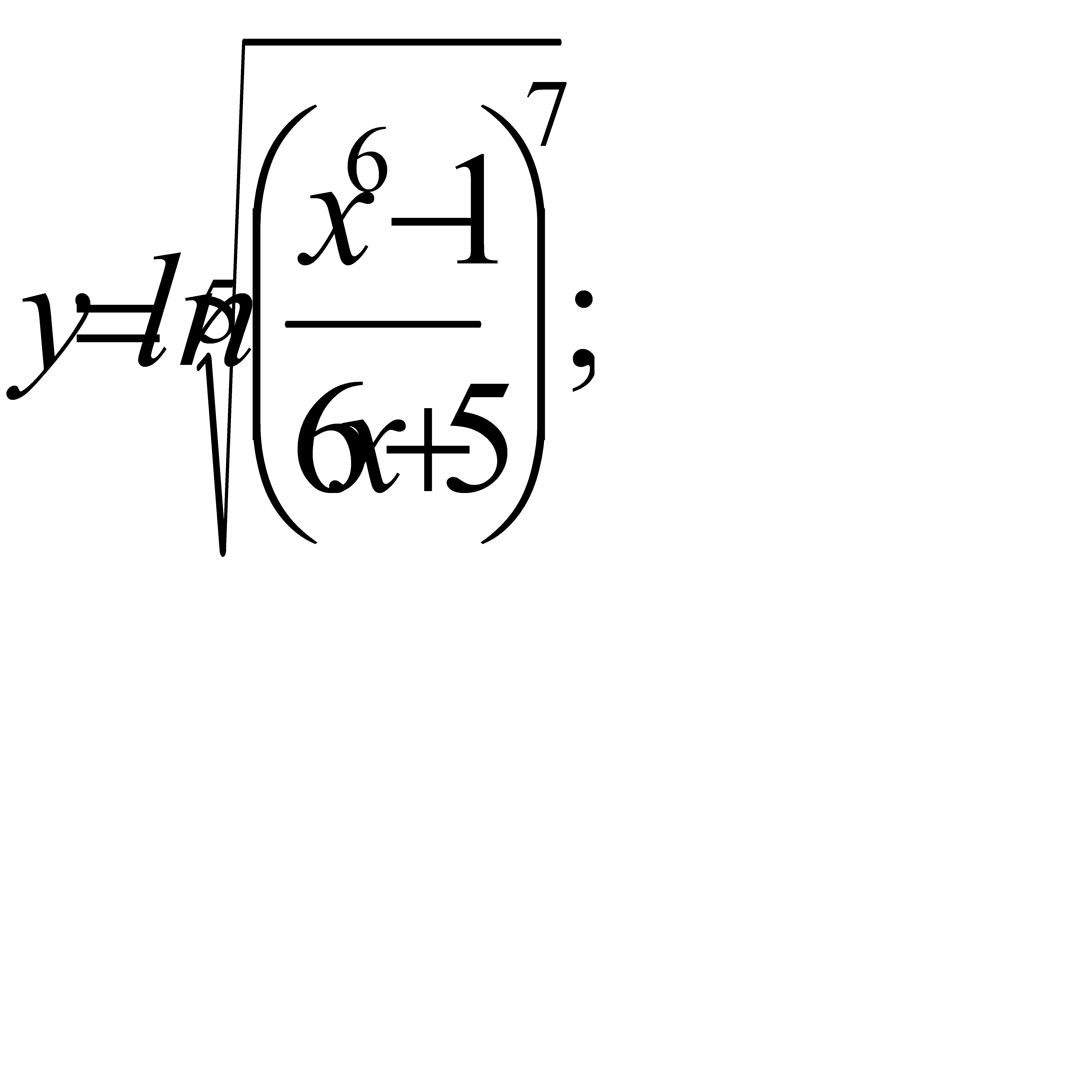
в) 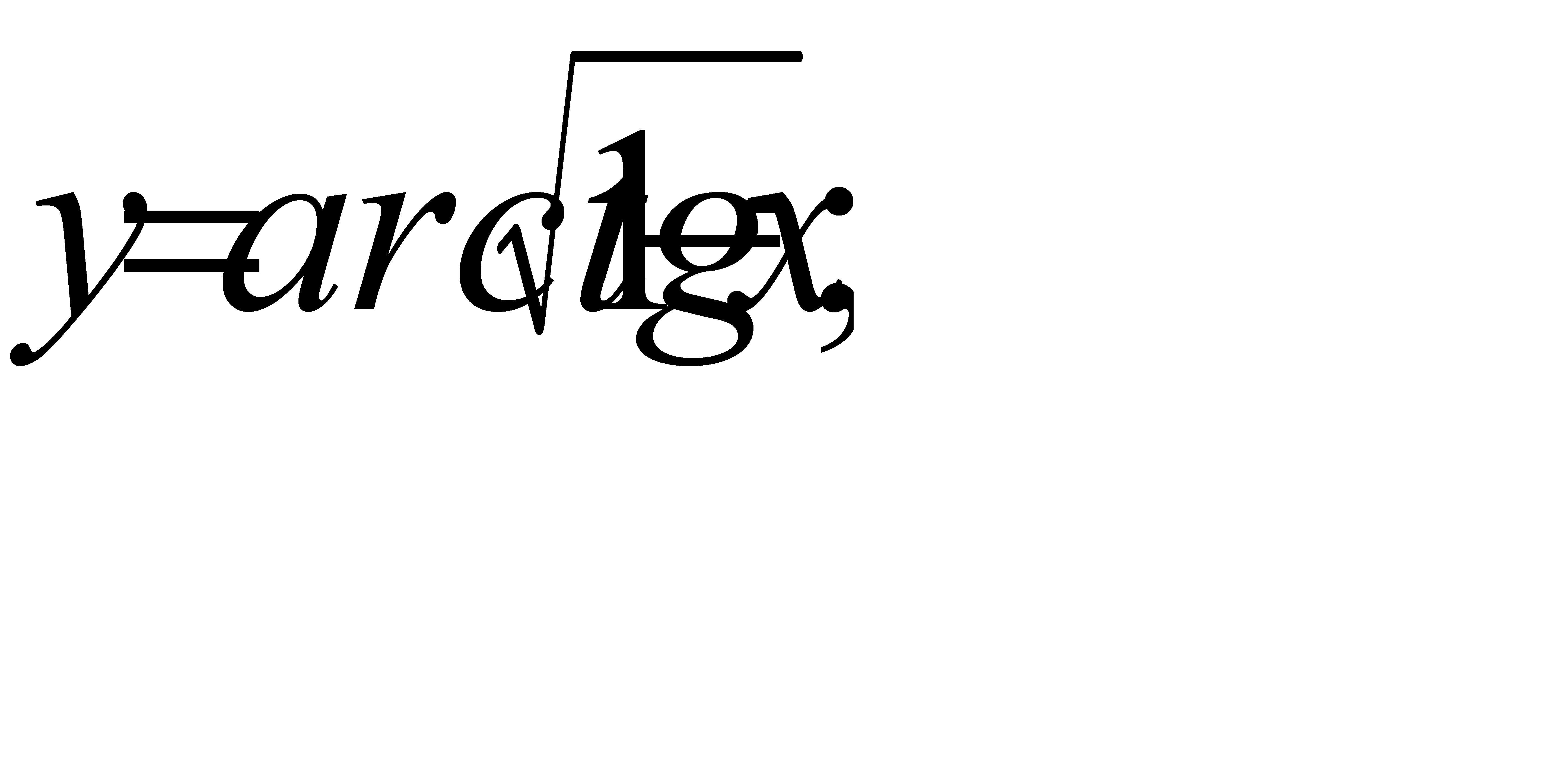 г)
г) 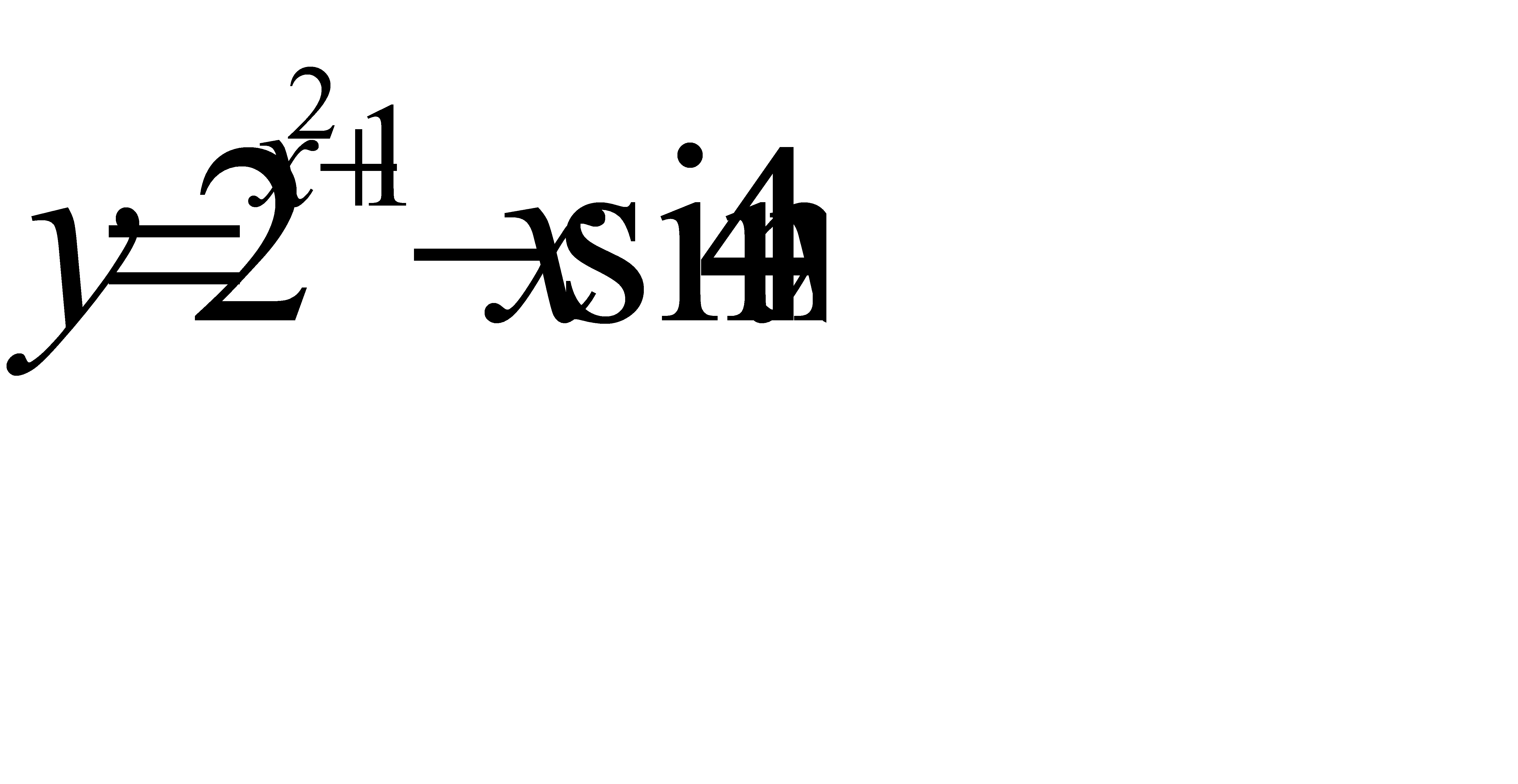 .
.
- а)
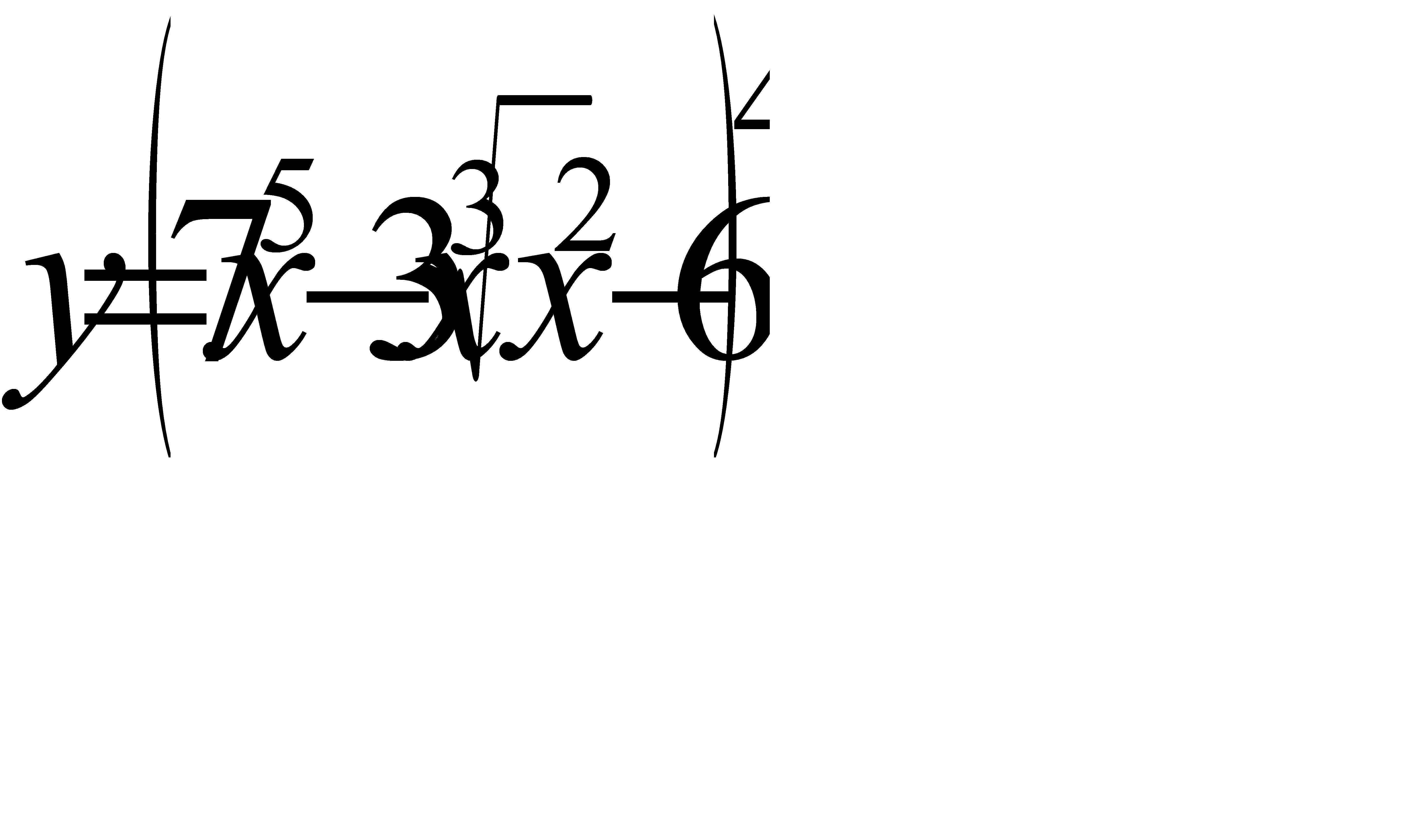 ; б)
; б) 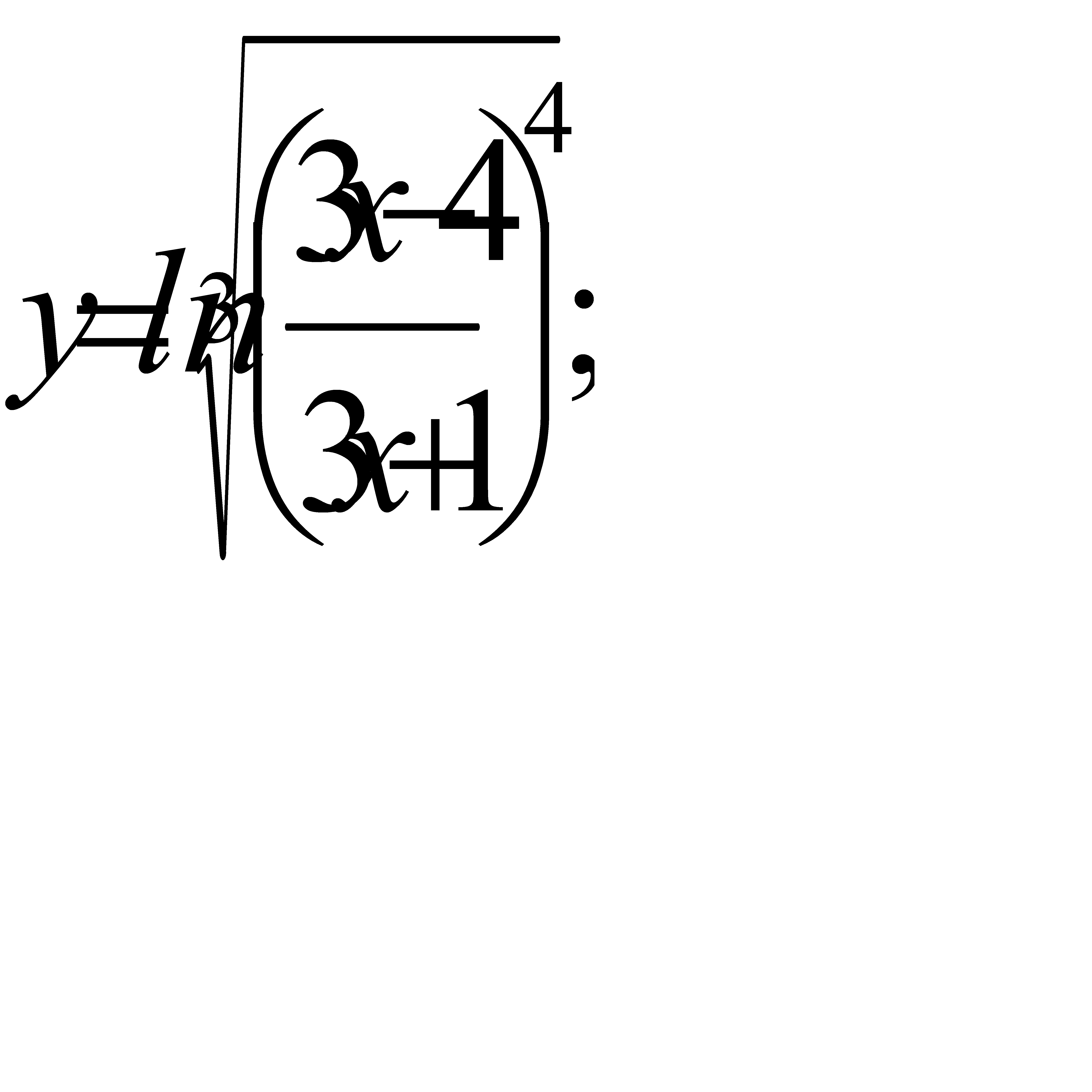
в) 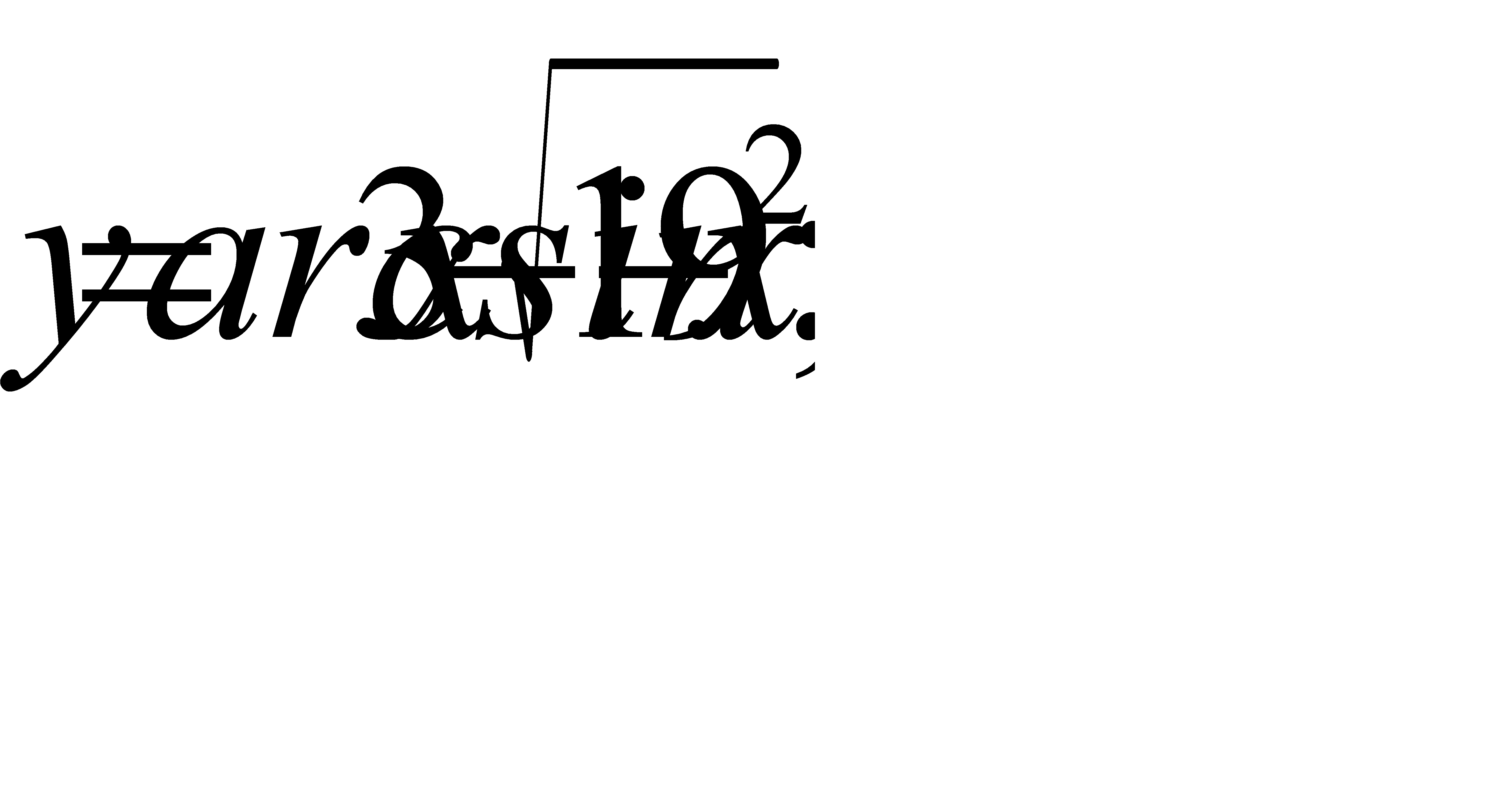 г)
г) 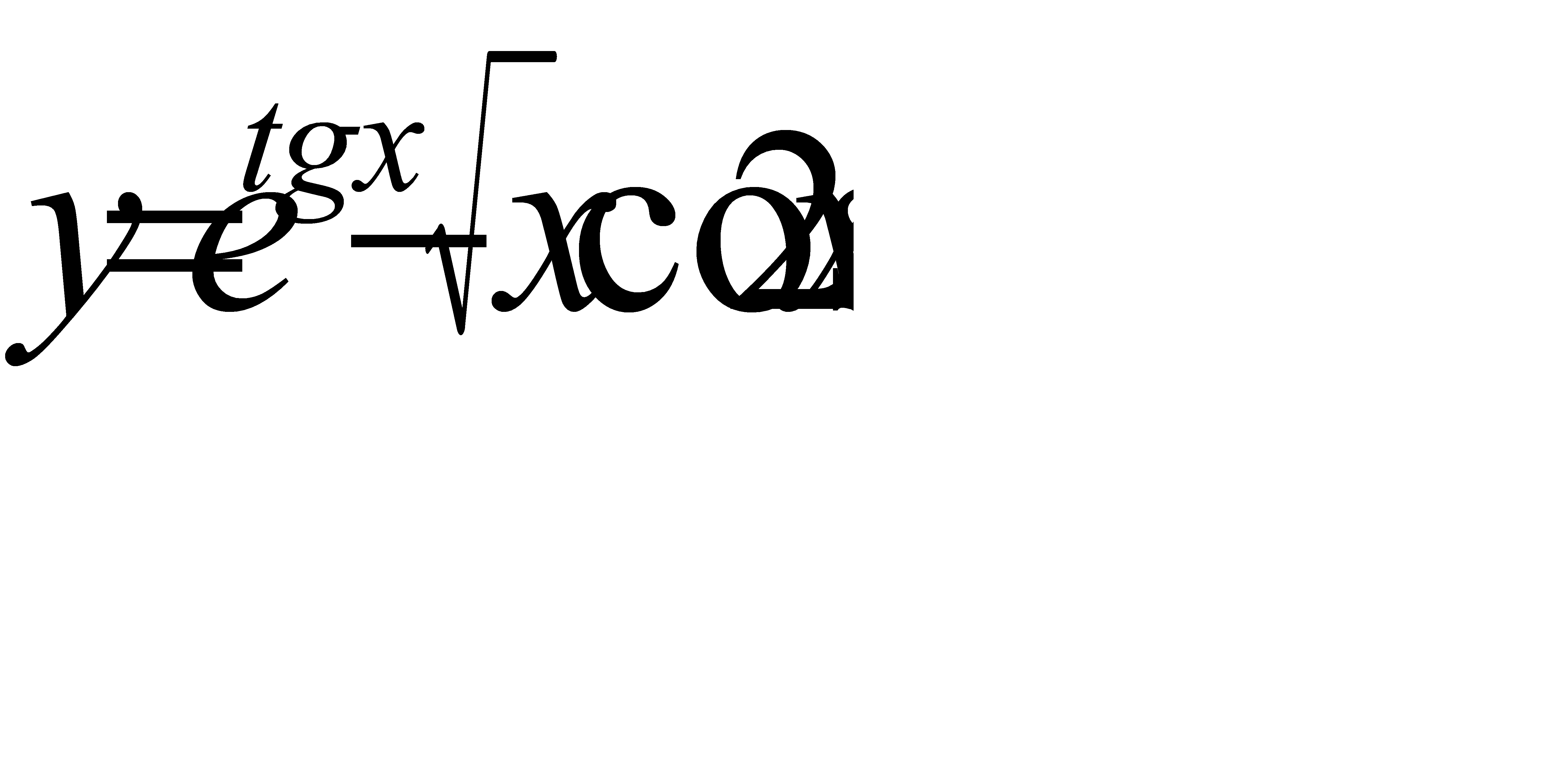 .
.
19. а) 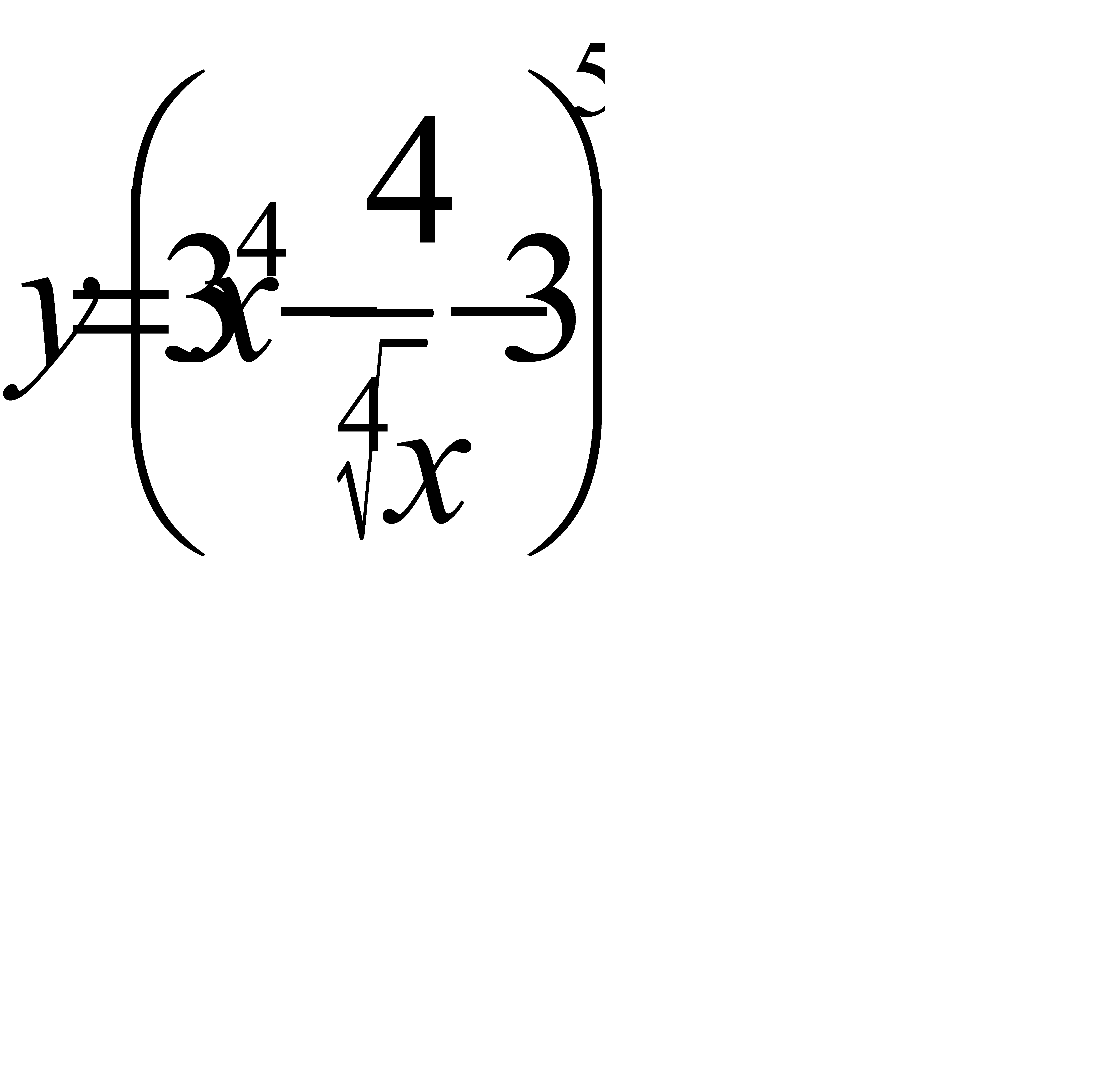 ; б)
; б) 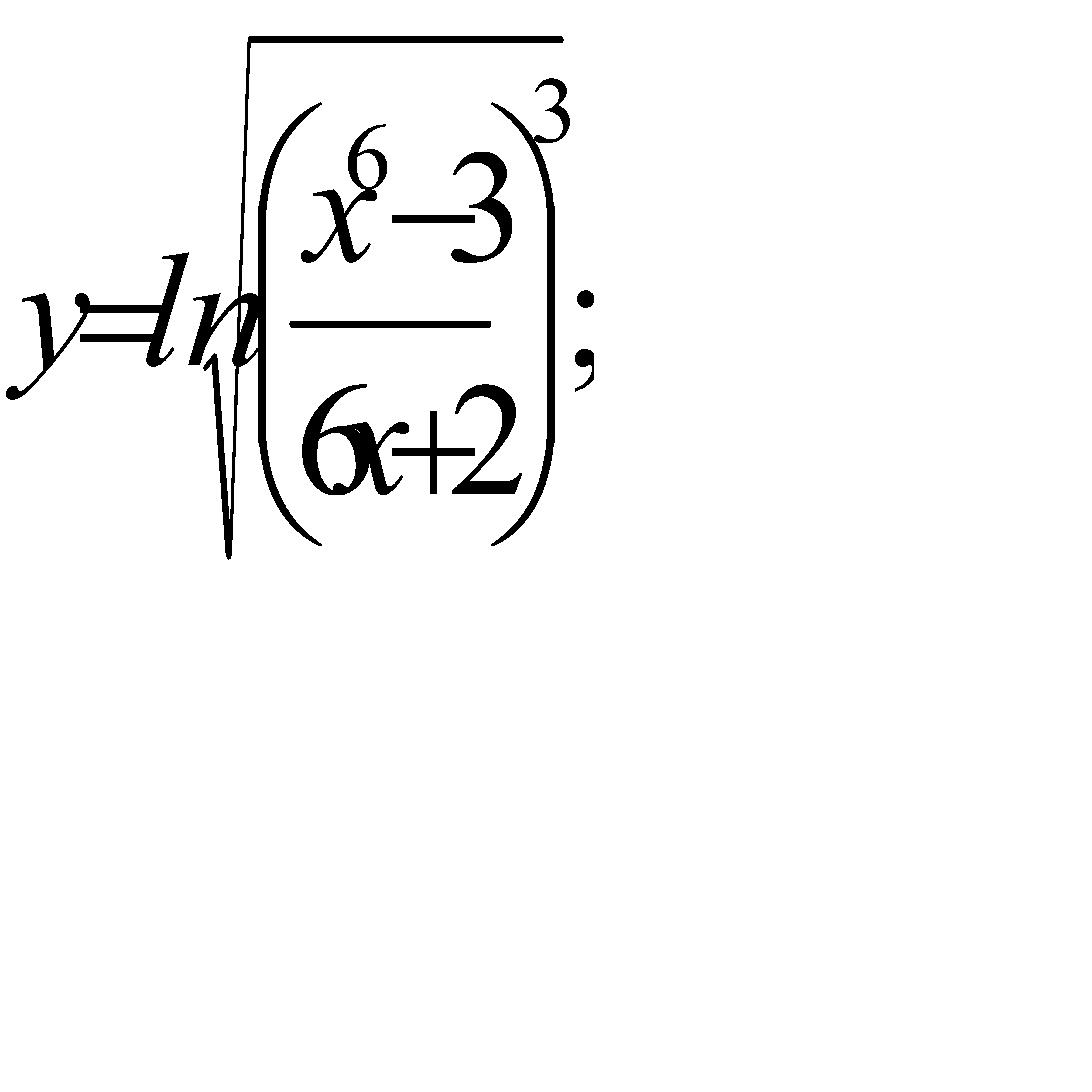
в) 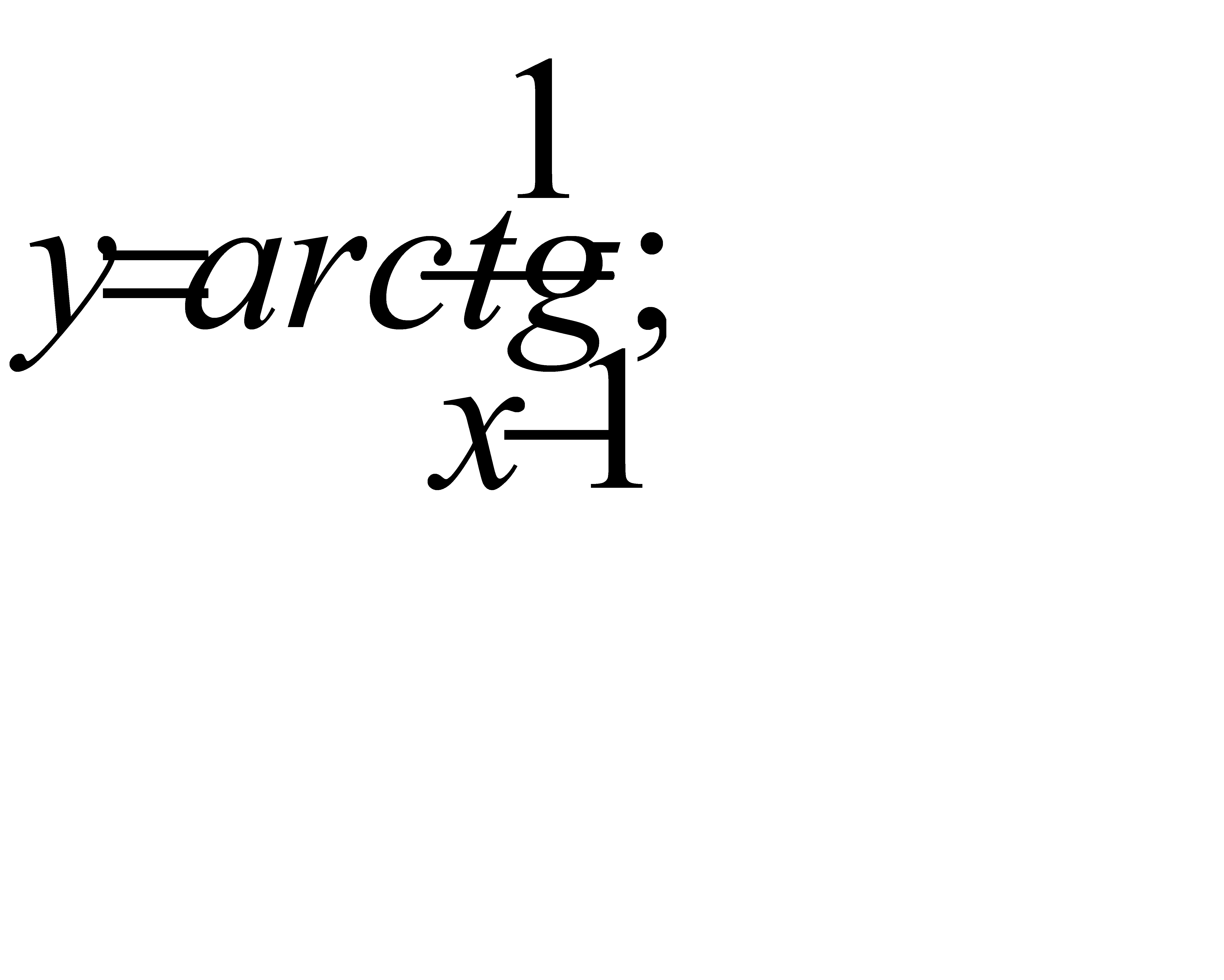 г)
г) 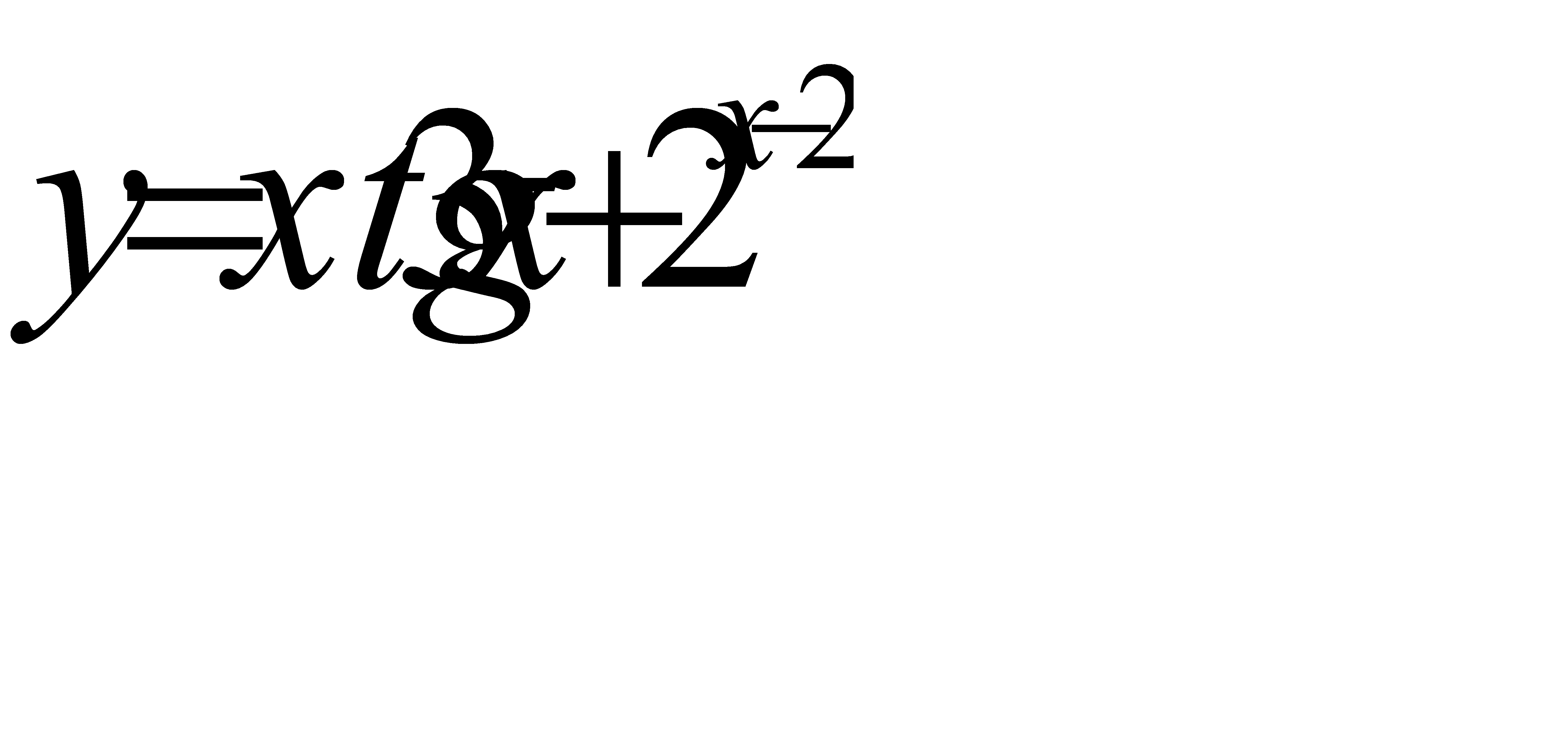 .
.
20. а) 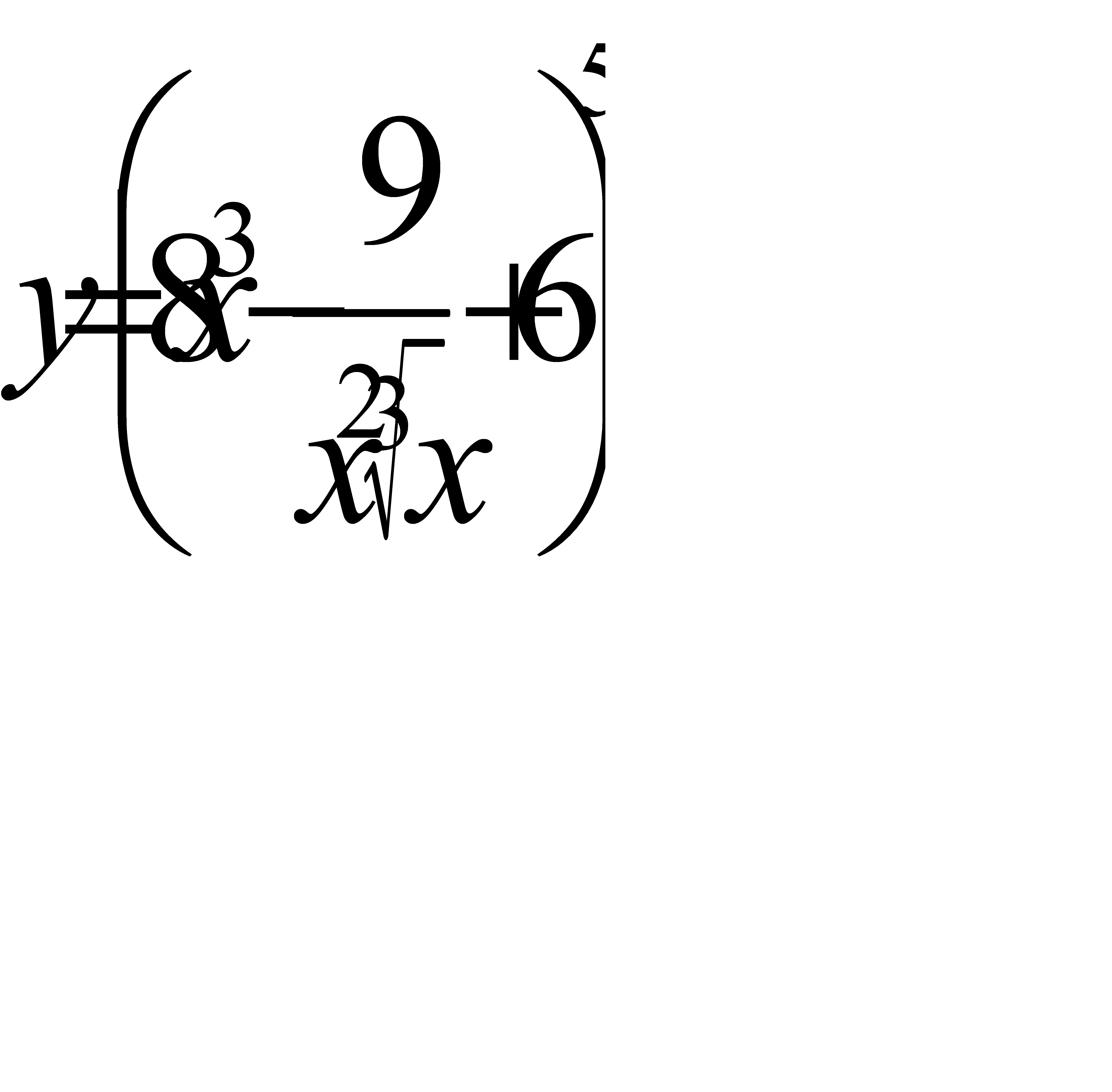 ; б)
; б) 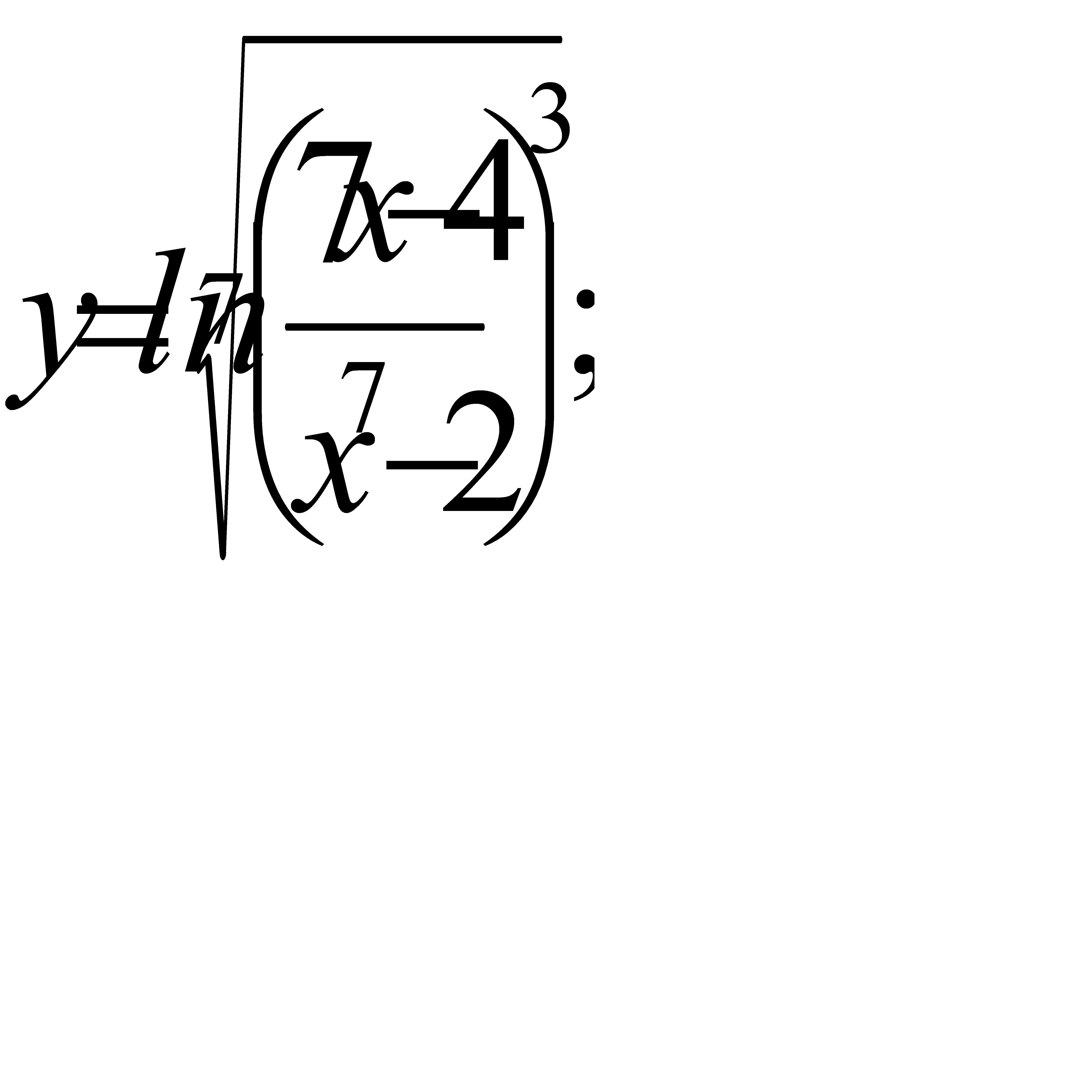
в)  г)
г) 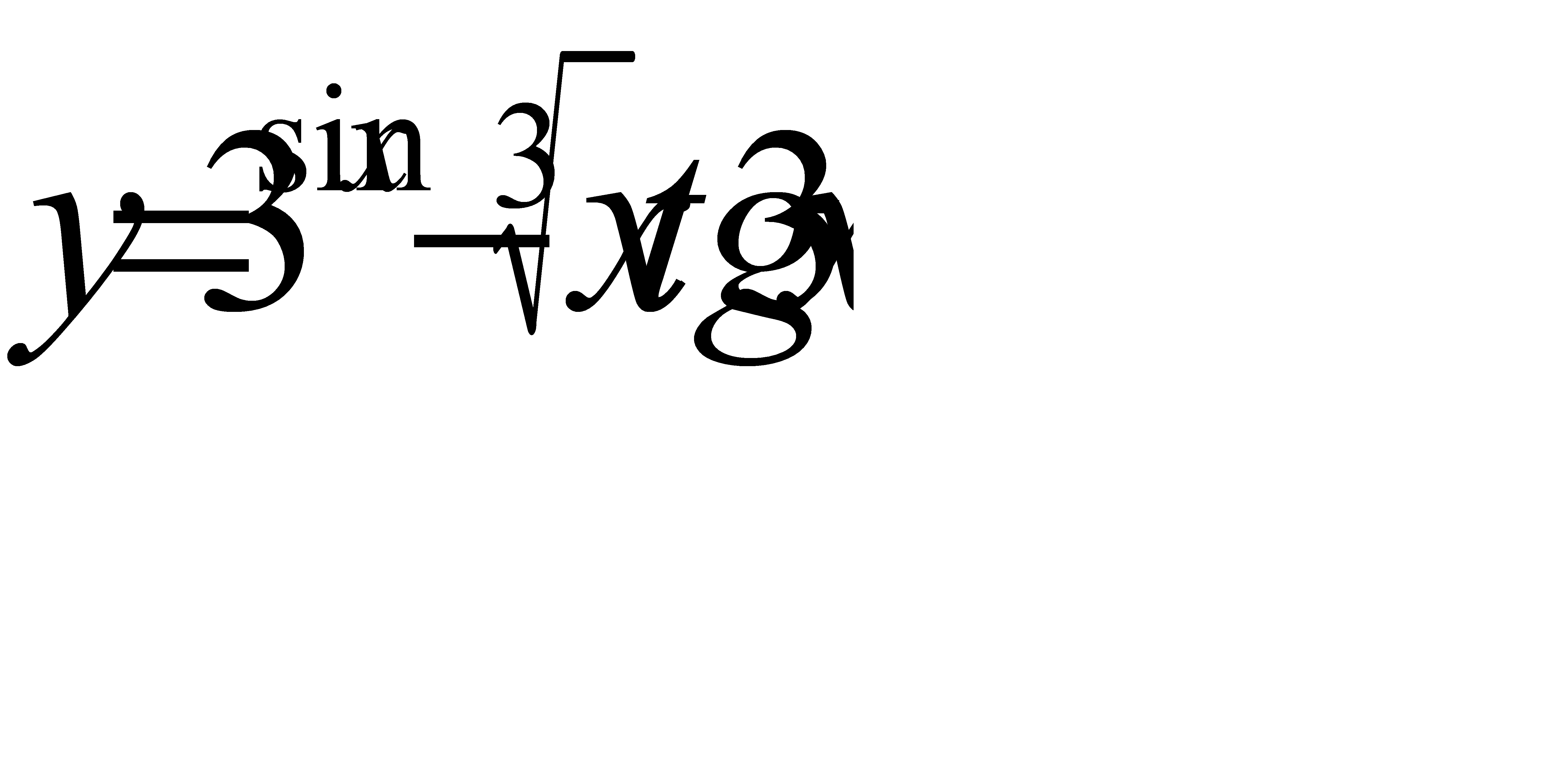 .
.
21-30. Вычислить приближенное значение 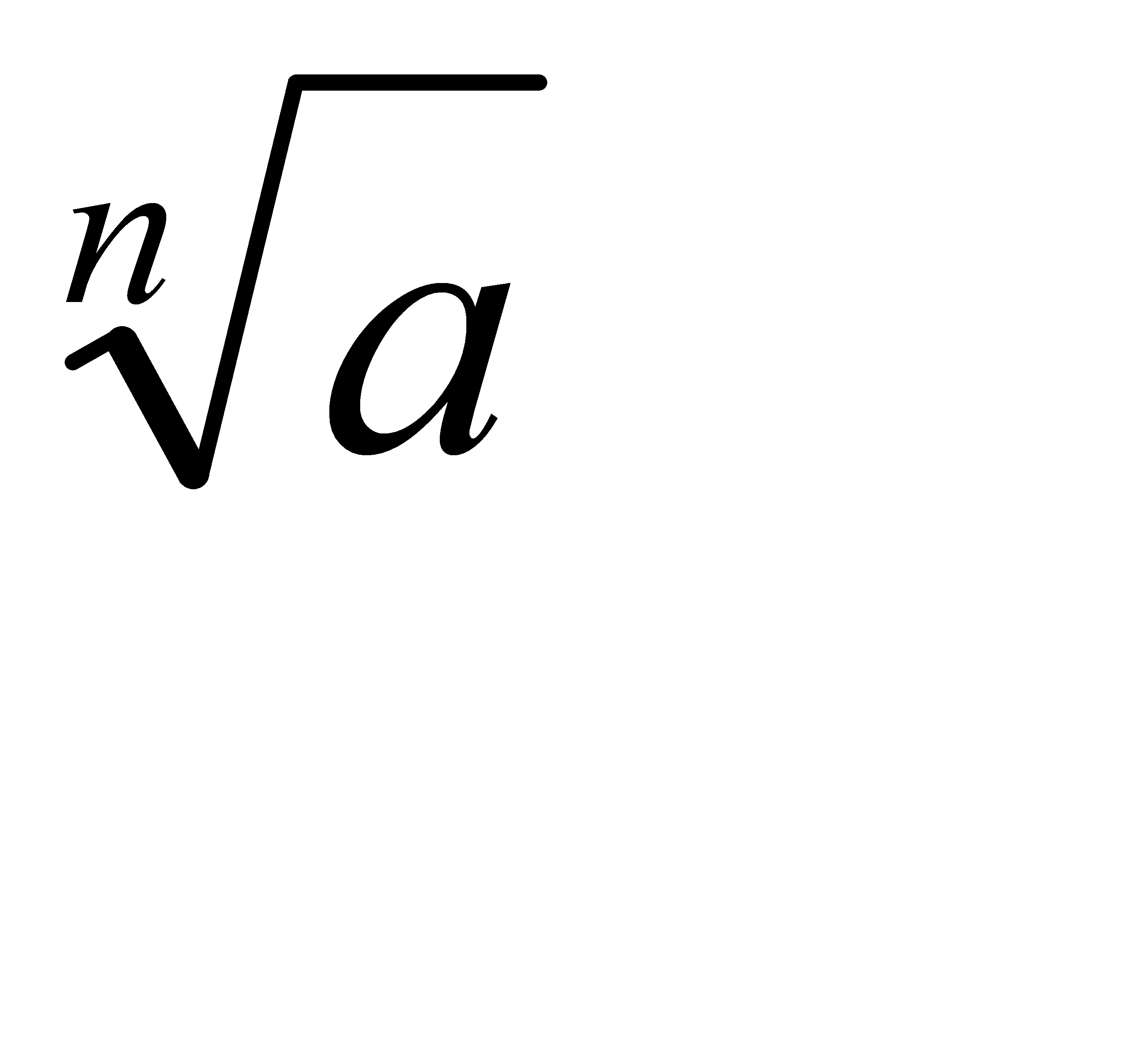 , заменив в точке
, заменив в точке 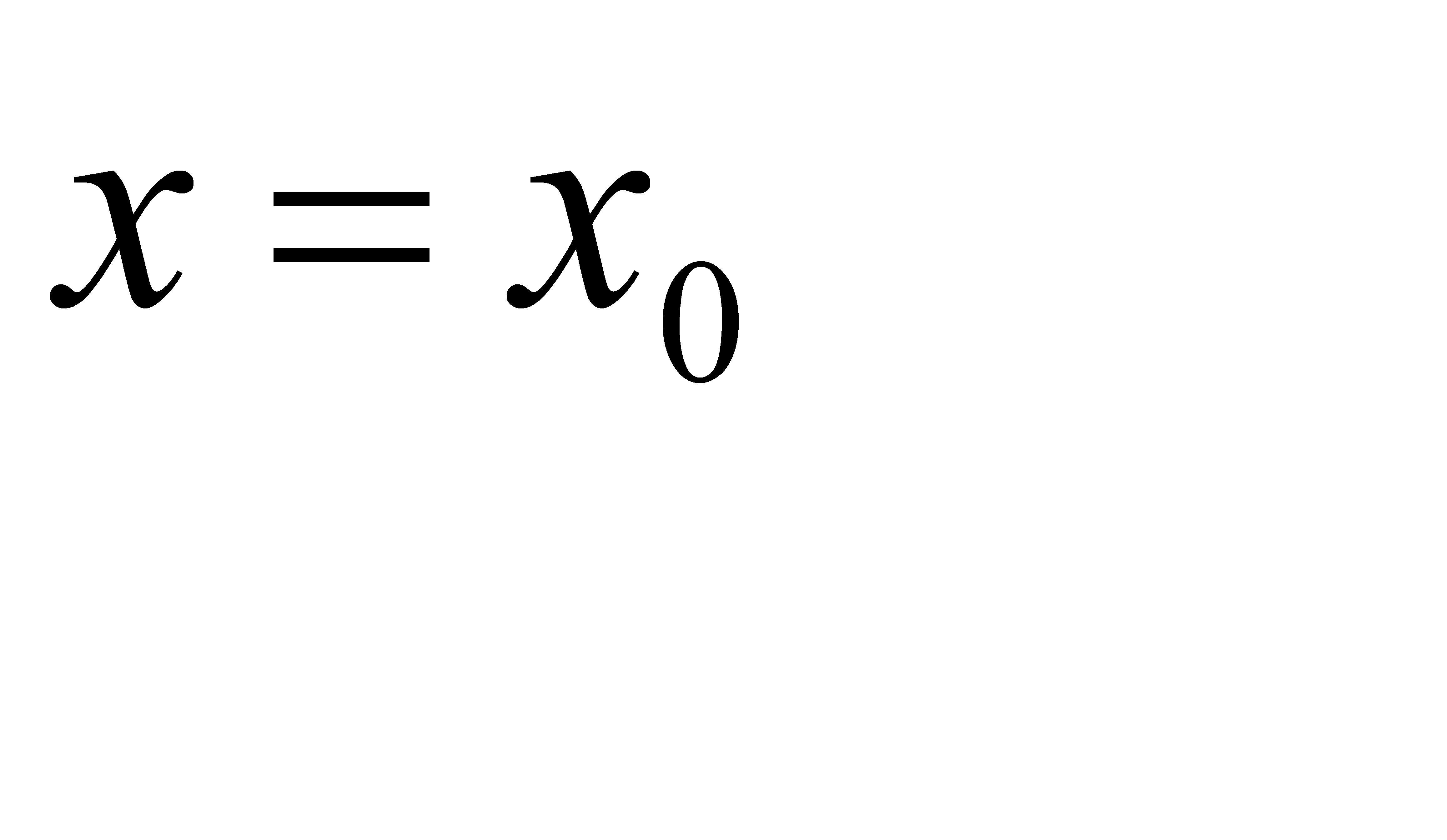 приращение функции
приращение функции 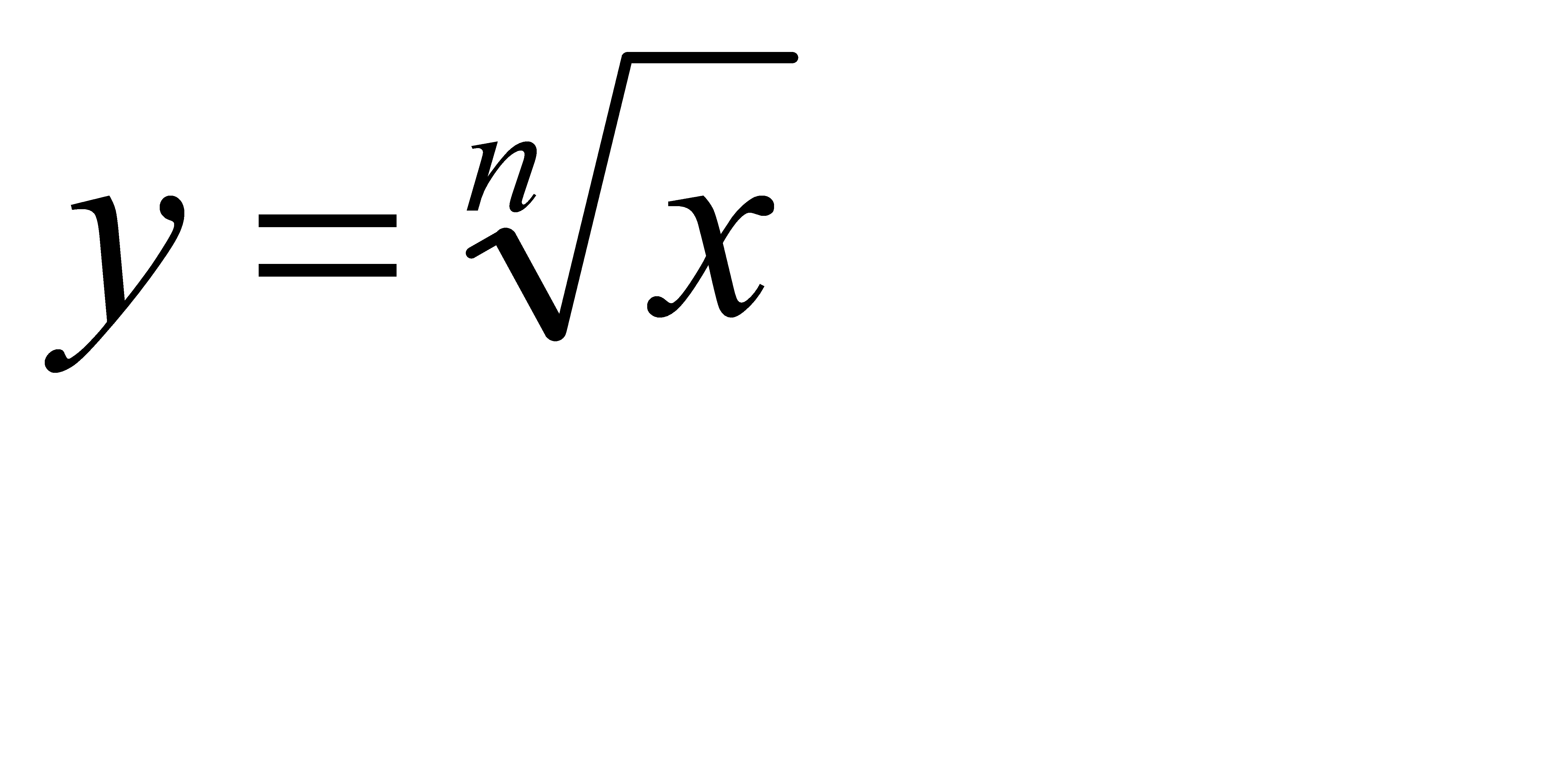 дифференциалом.
дифференциалом.
23. 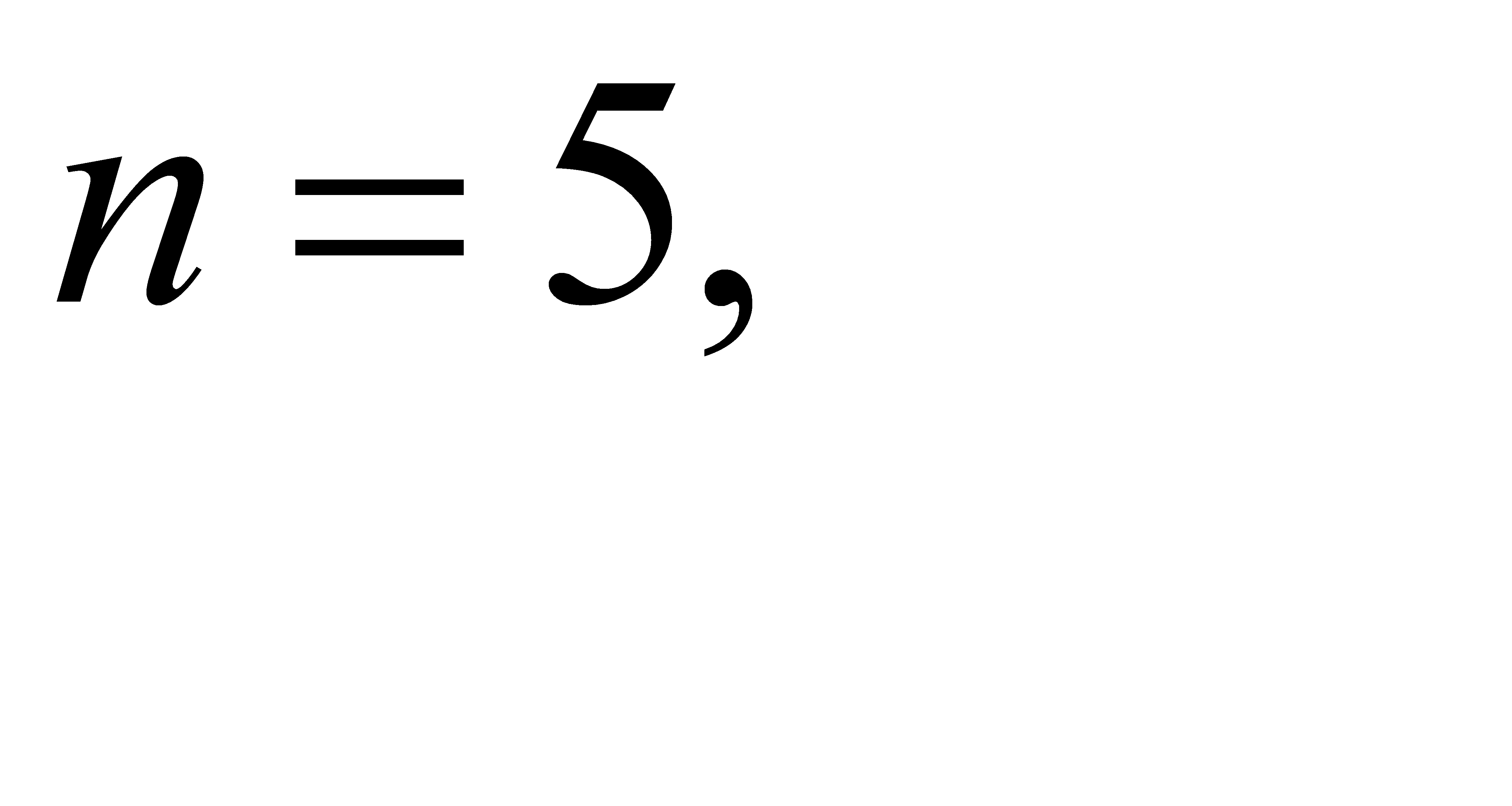


24. 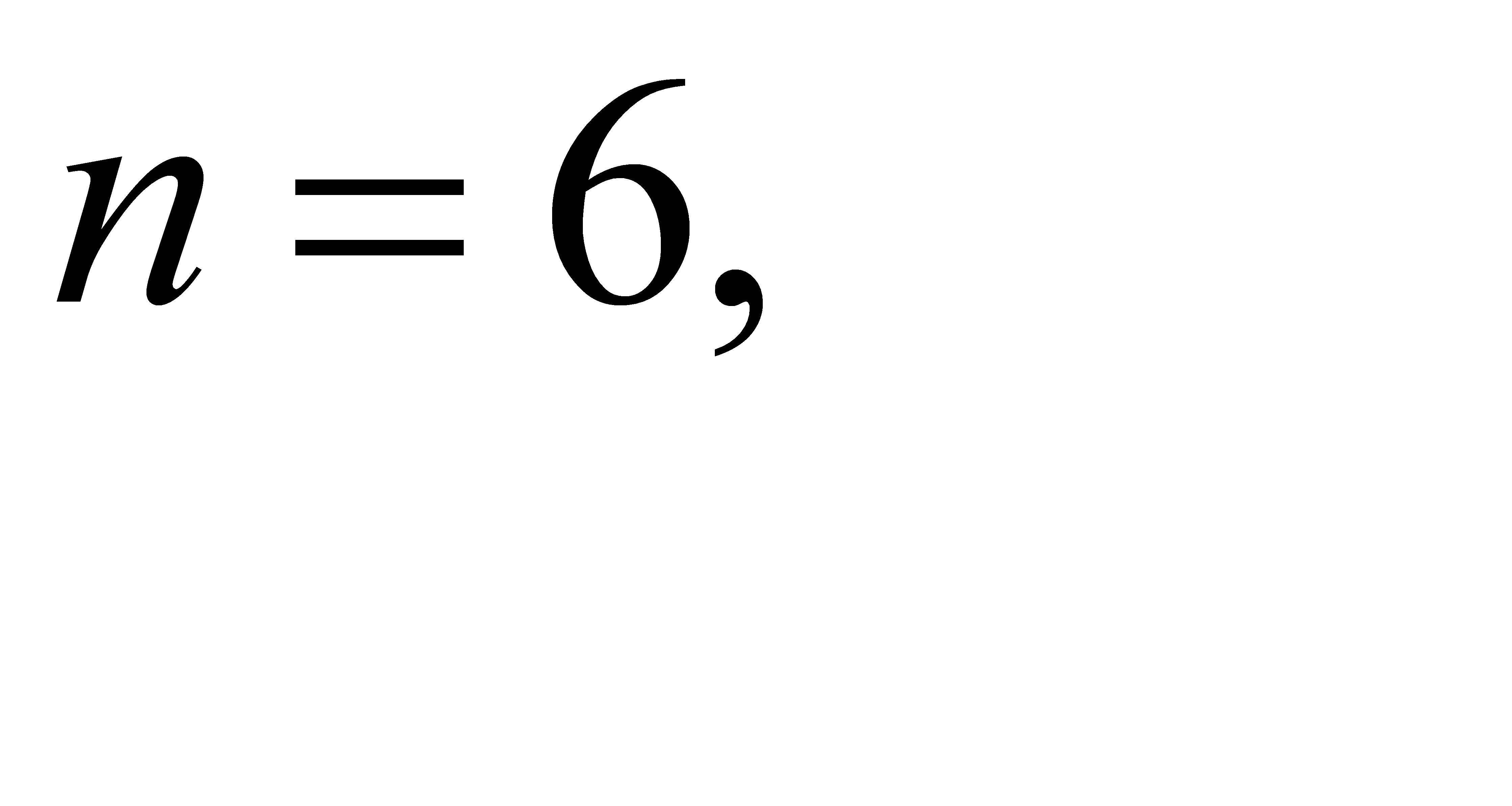


25. 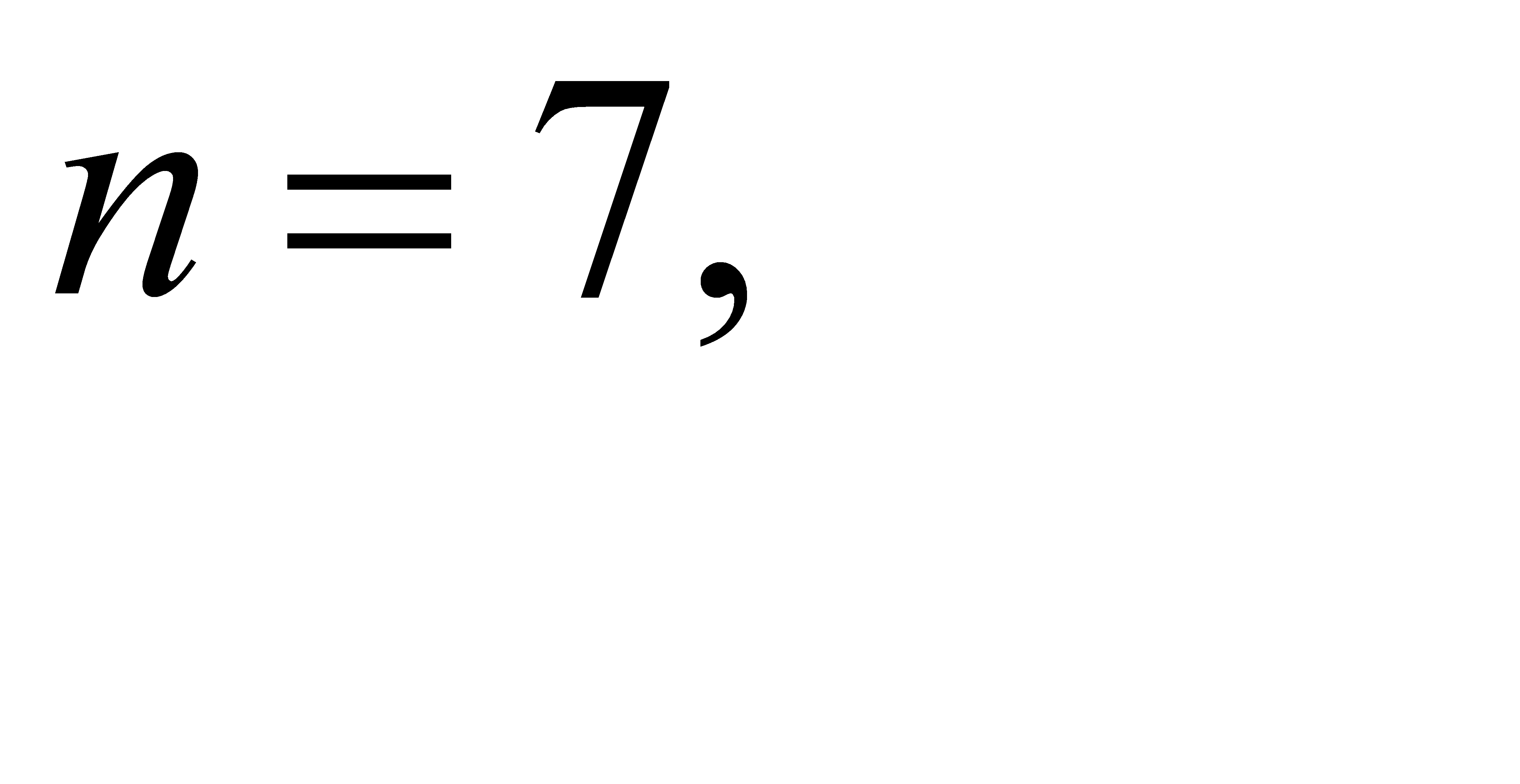


26. 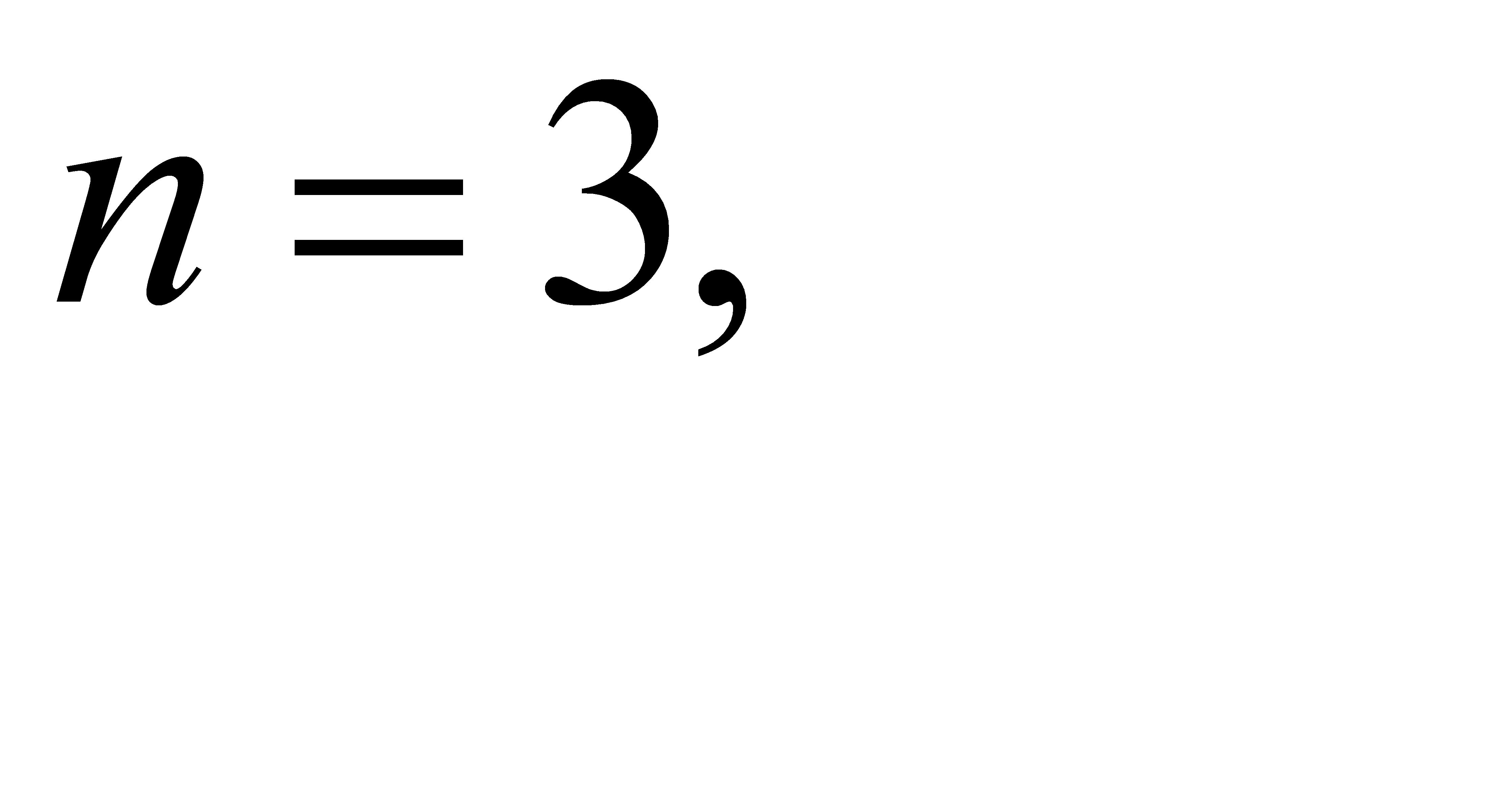


27. 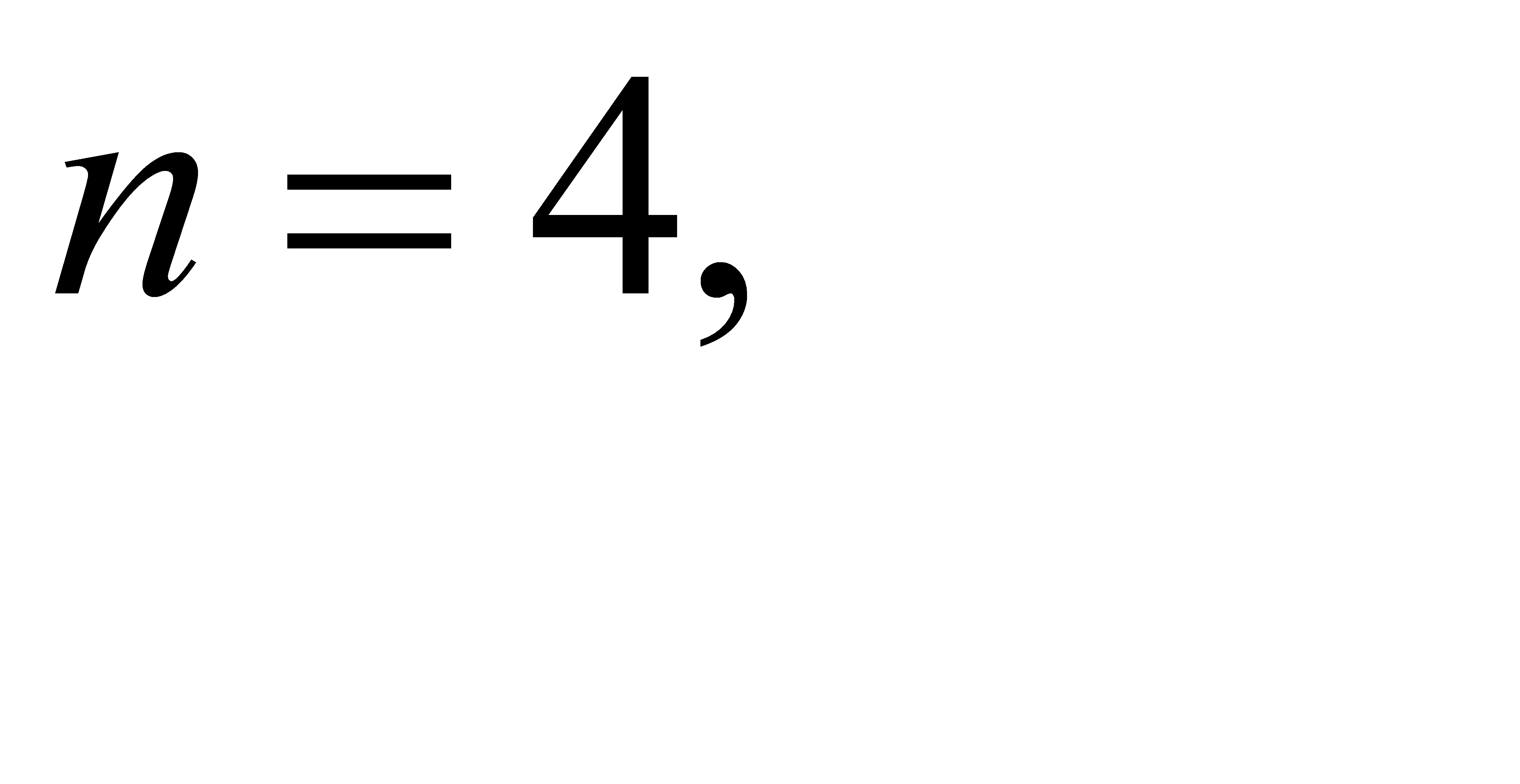
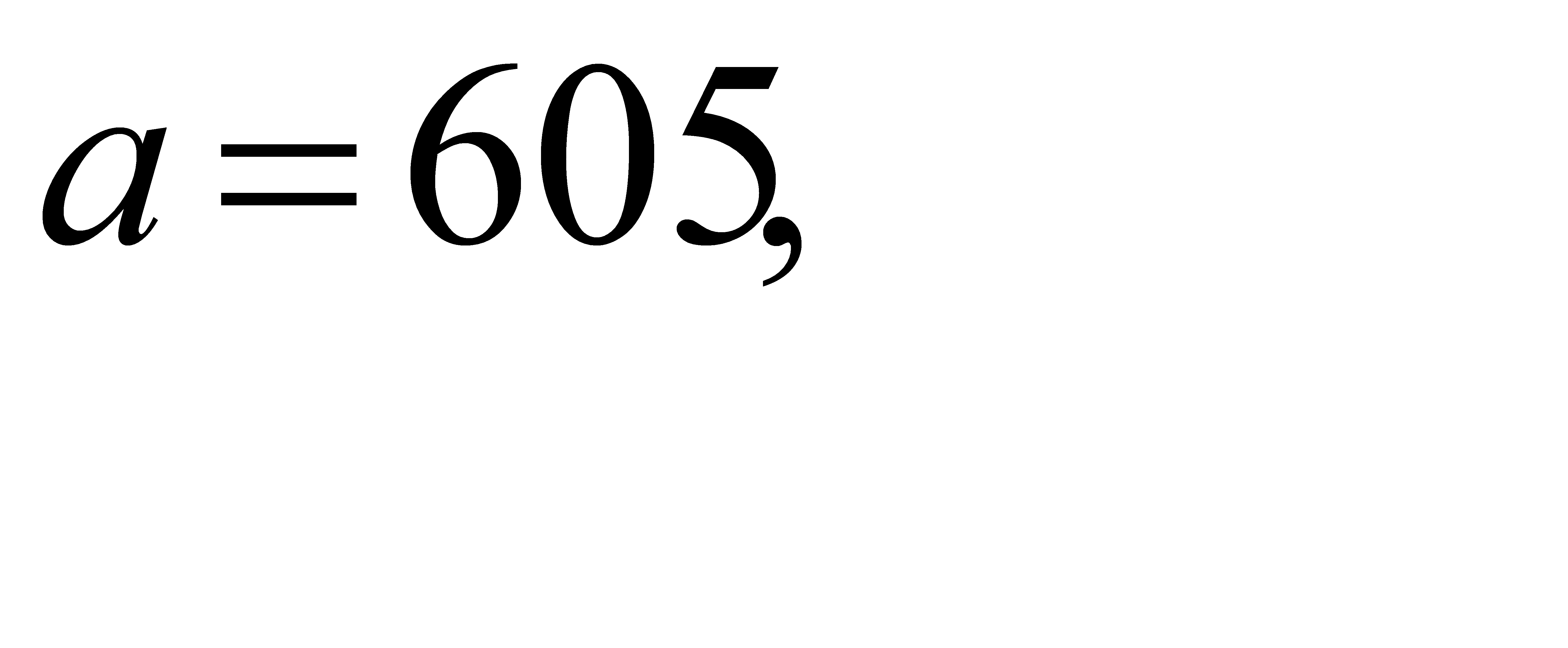

28. 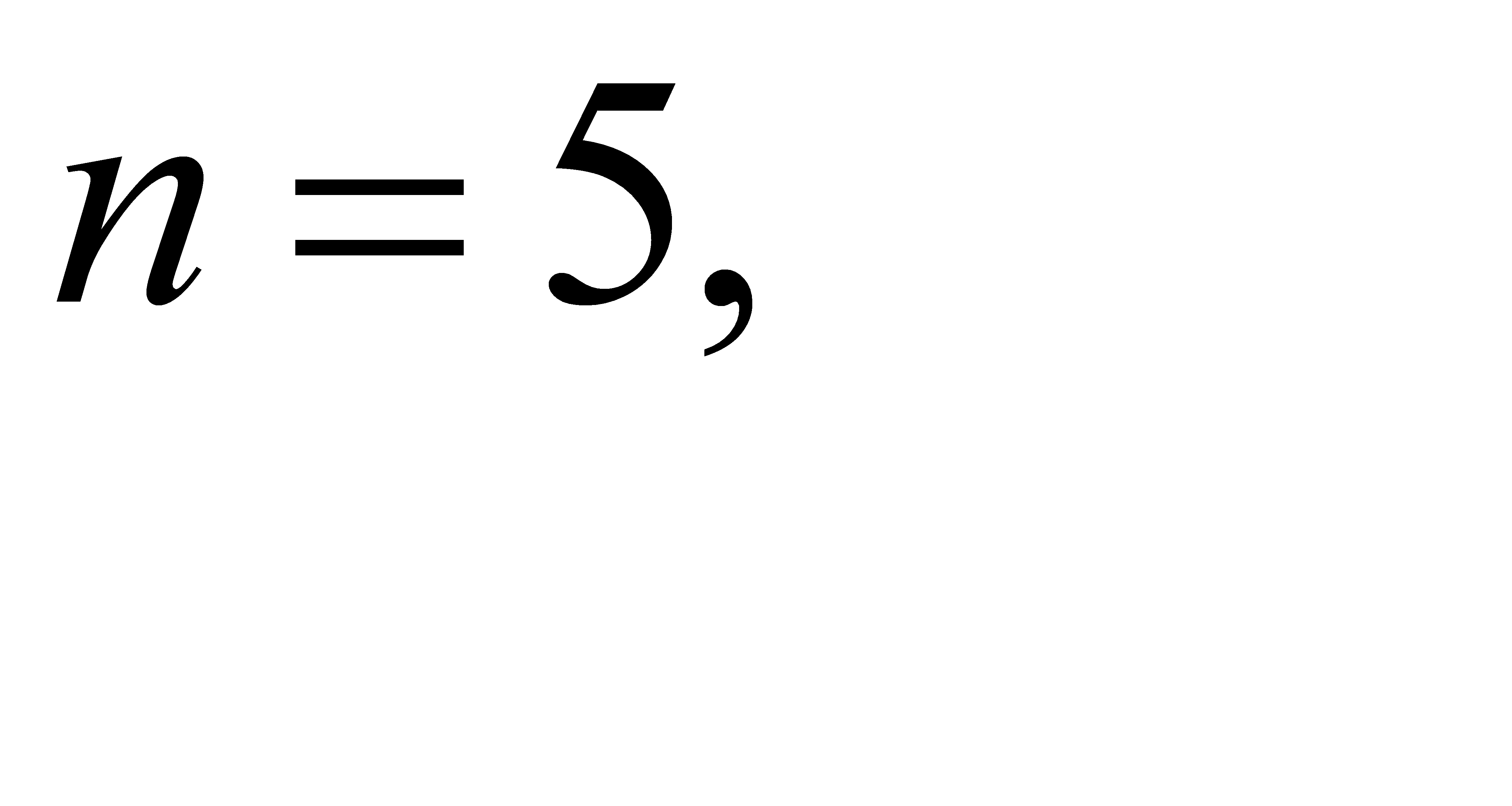
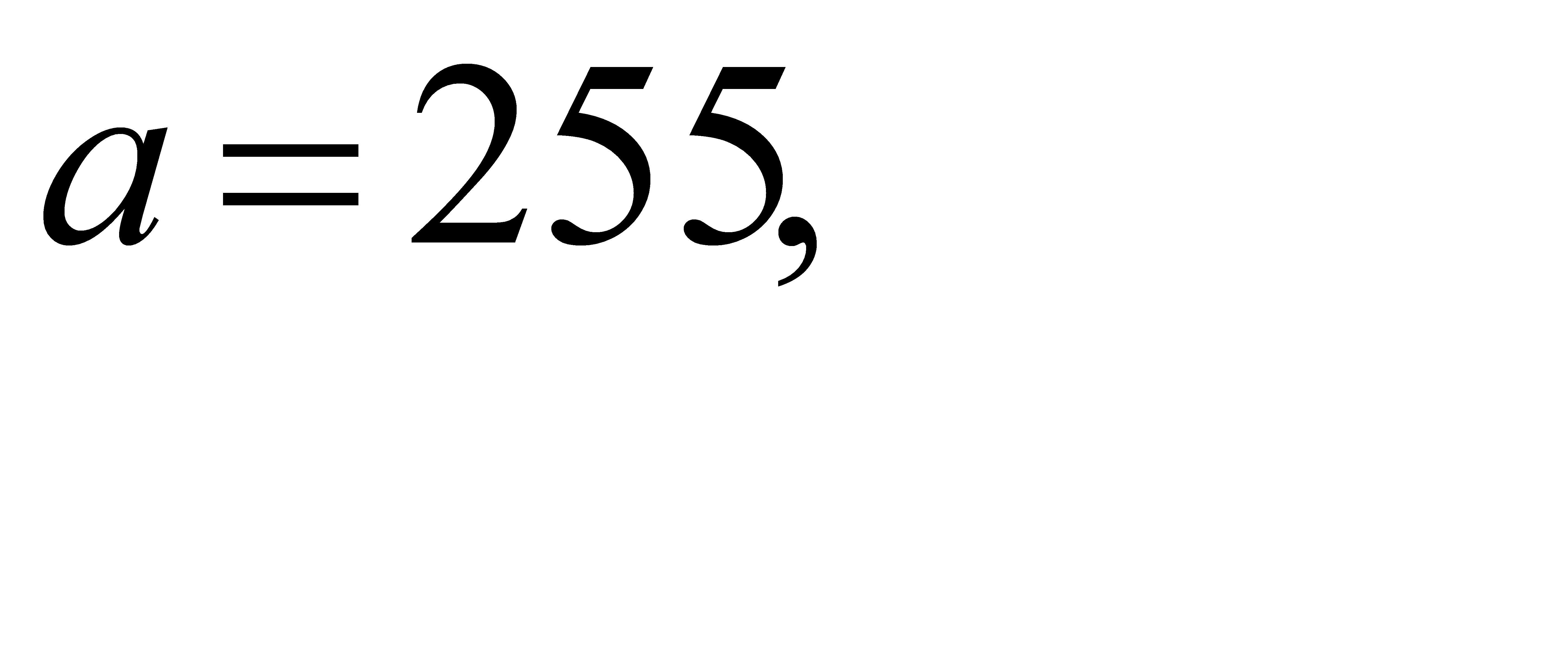

29. 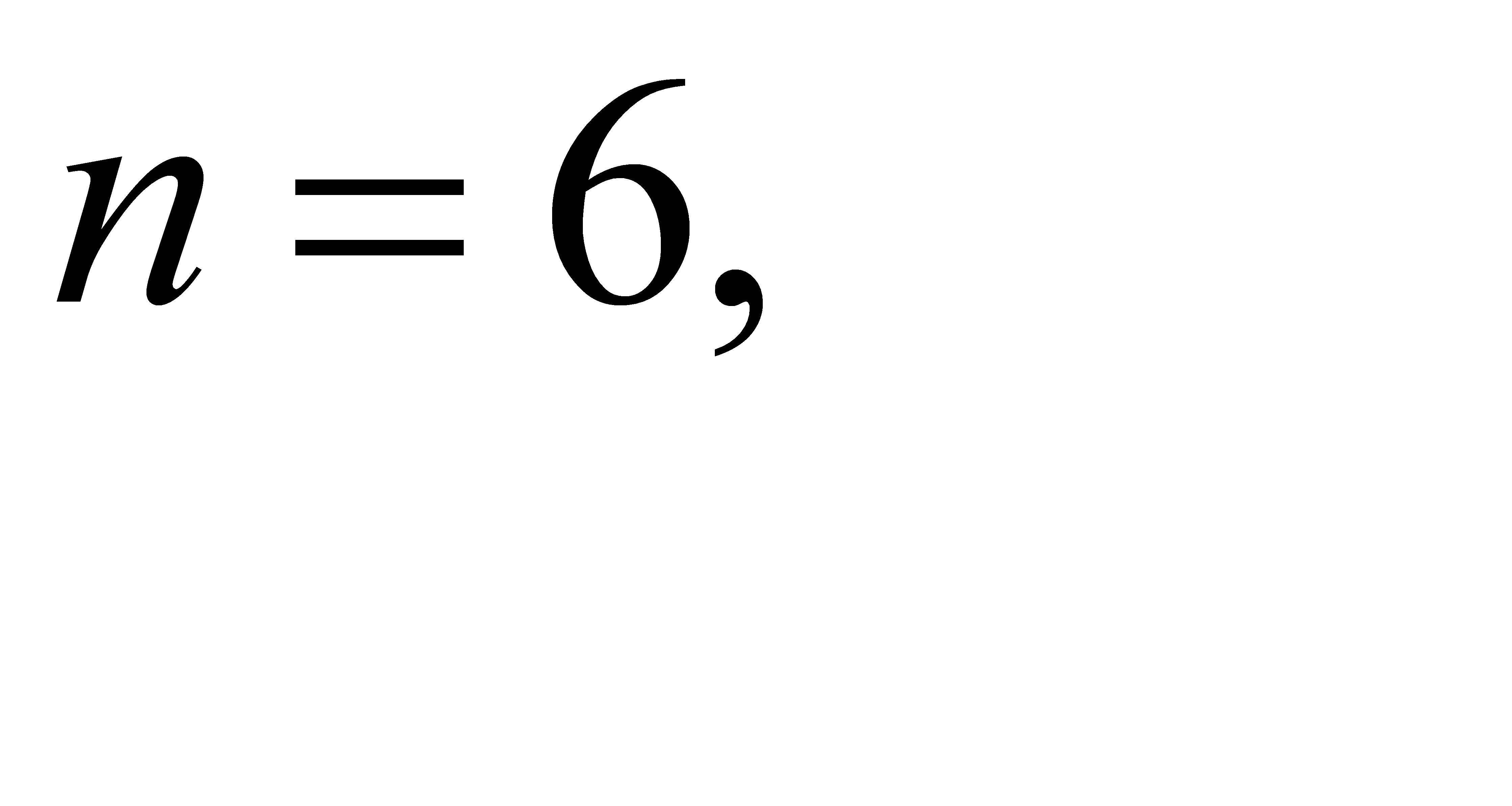


30. 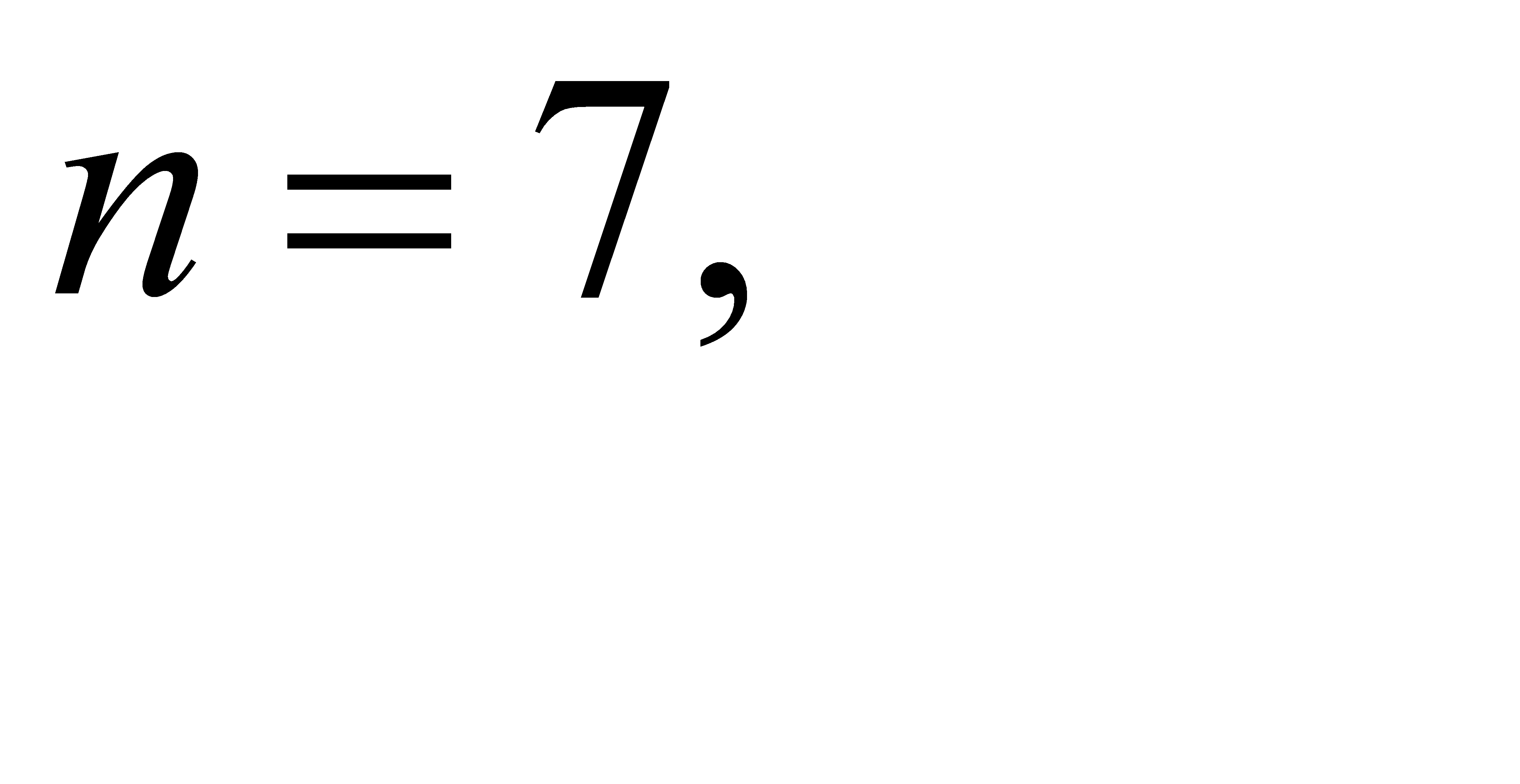
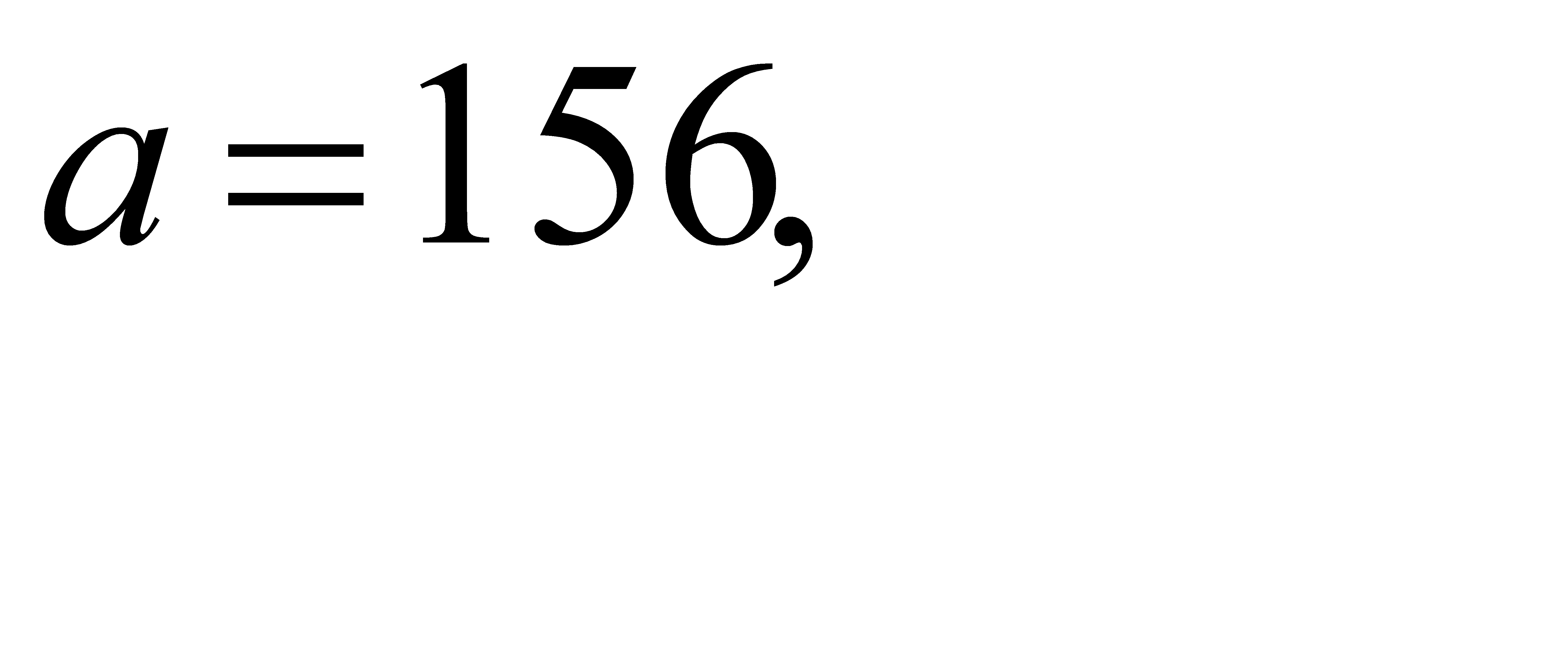

31-40. Исследовать функцию 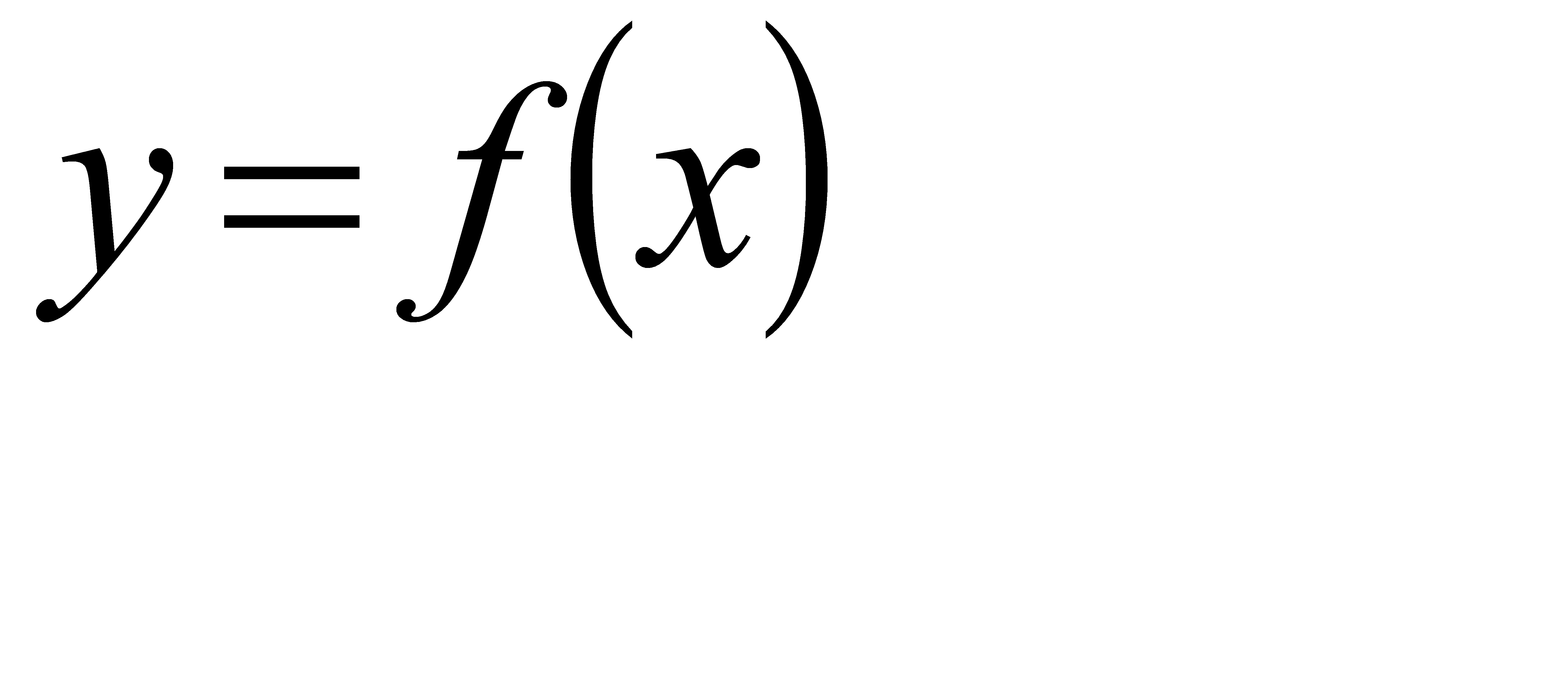 и построить ее график.
и построить ее график.
31. 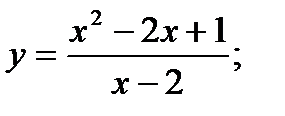 32.
32. 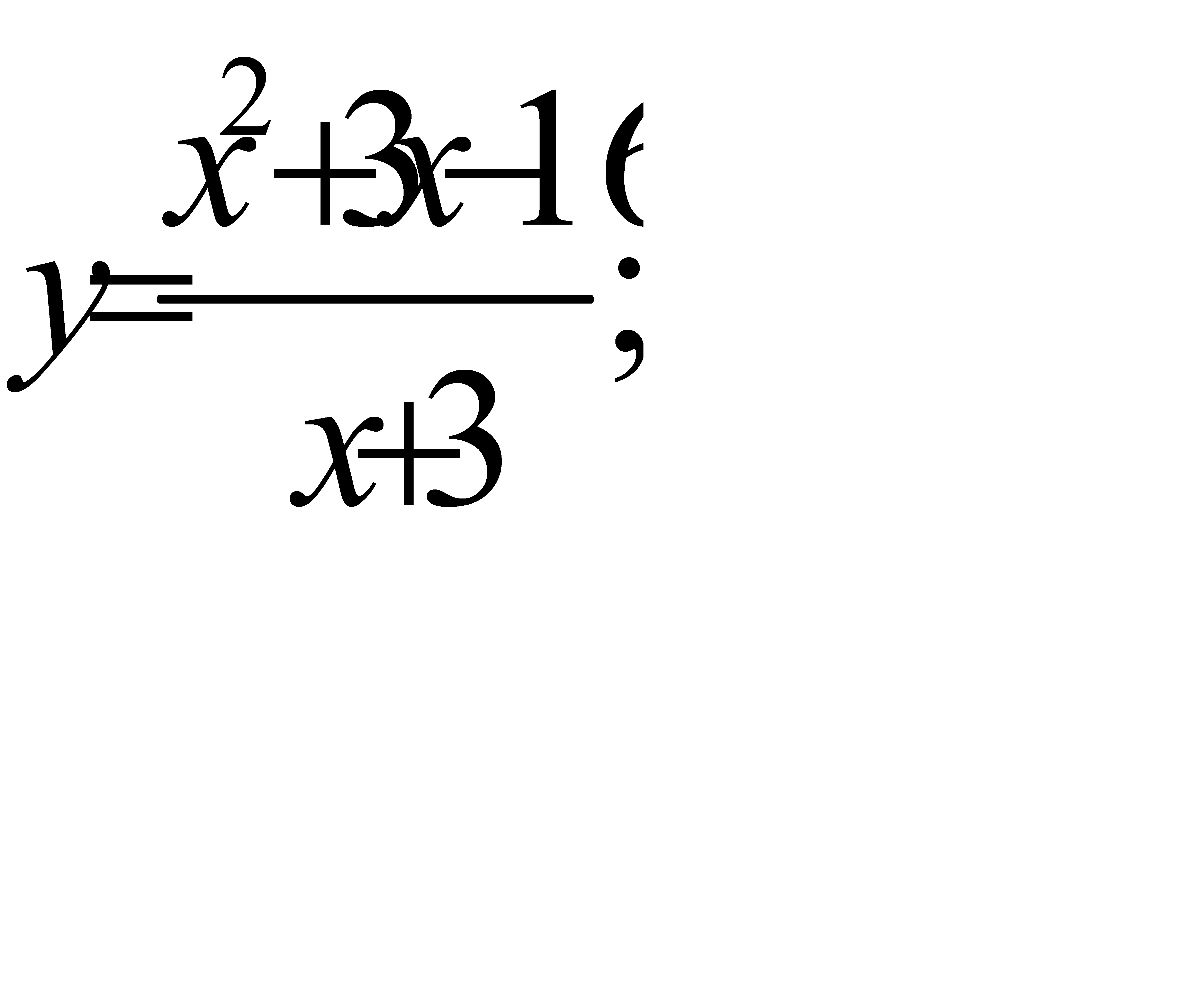
33. 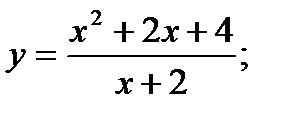 34.
34. 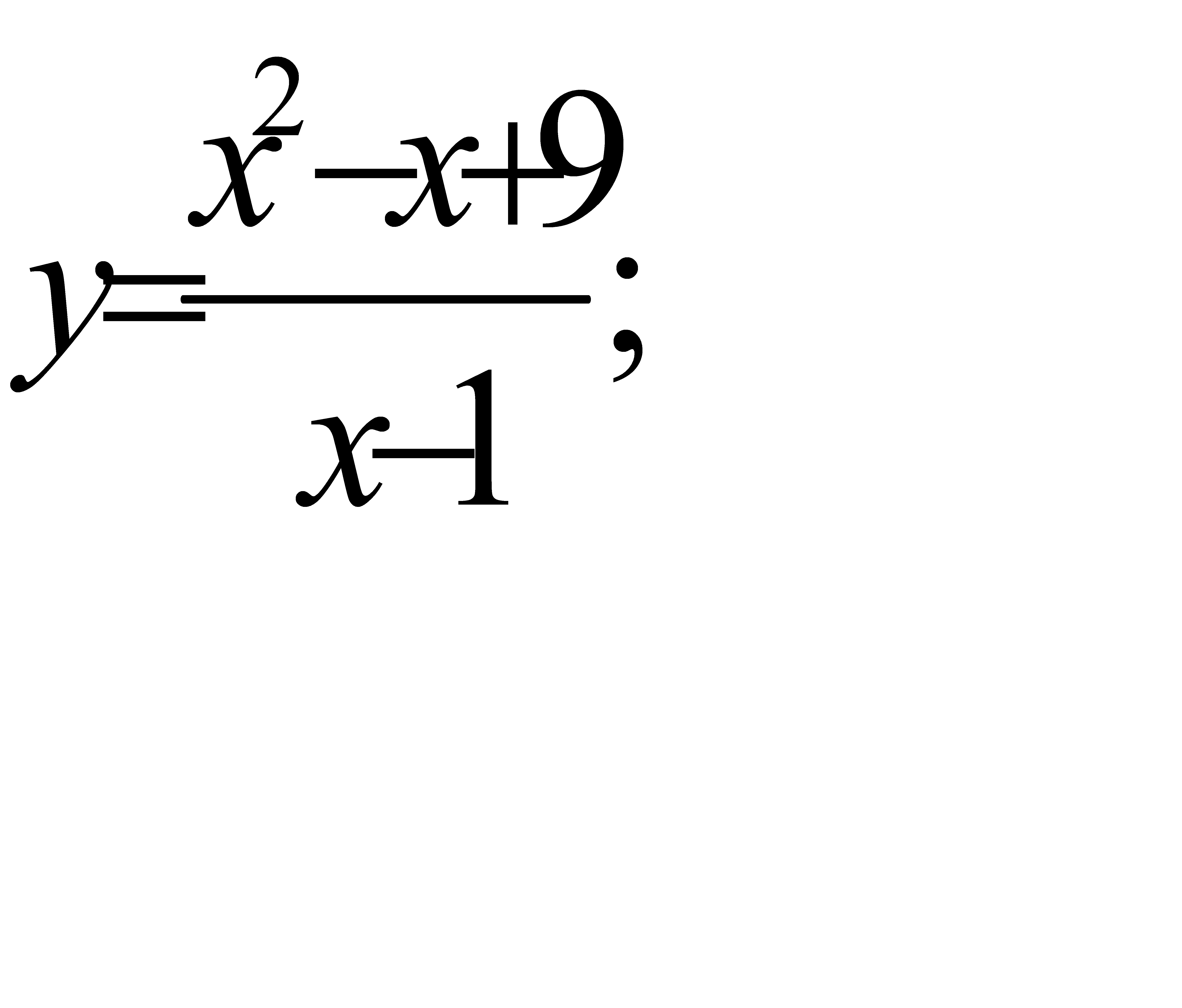
35. 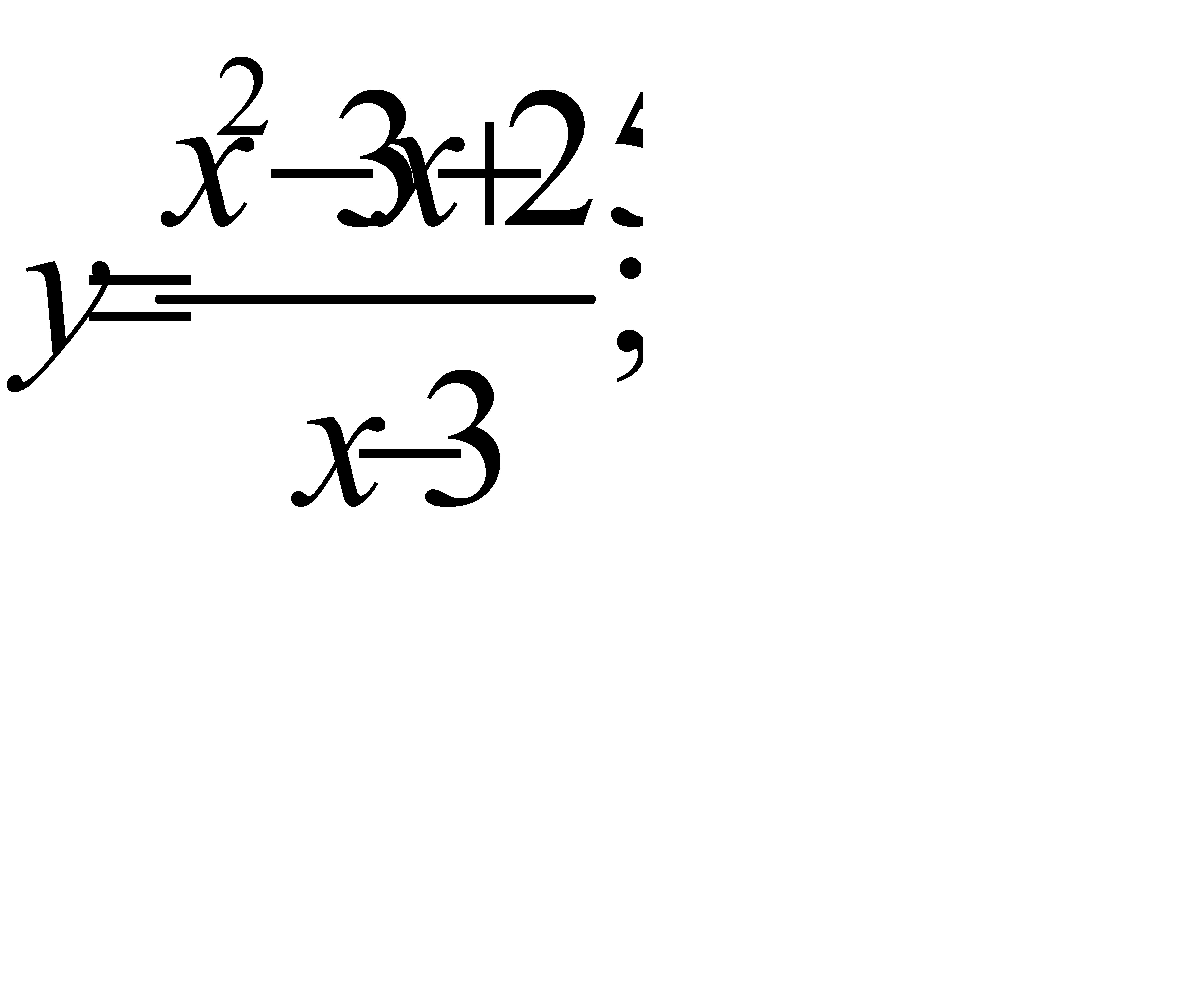 36.
36. 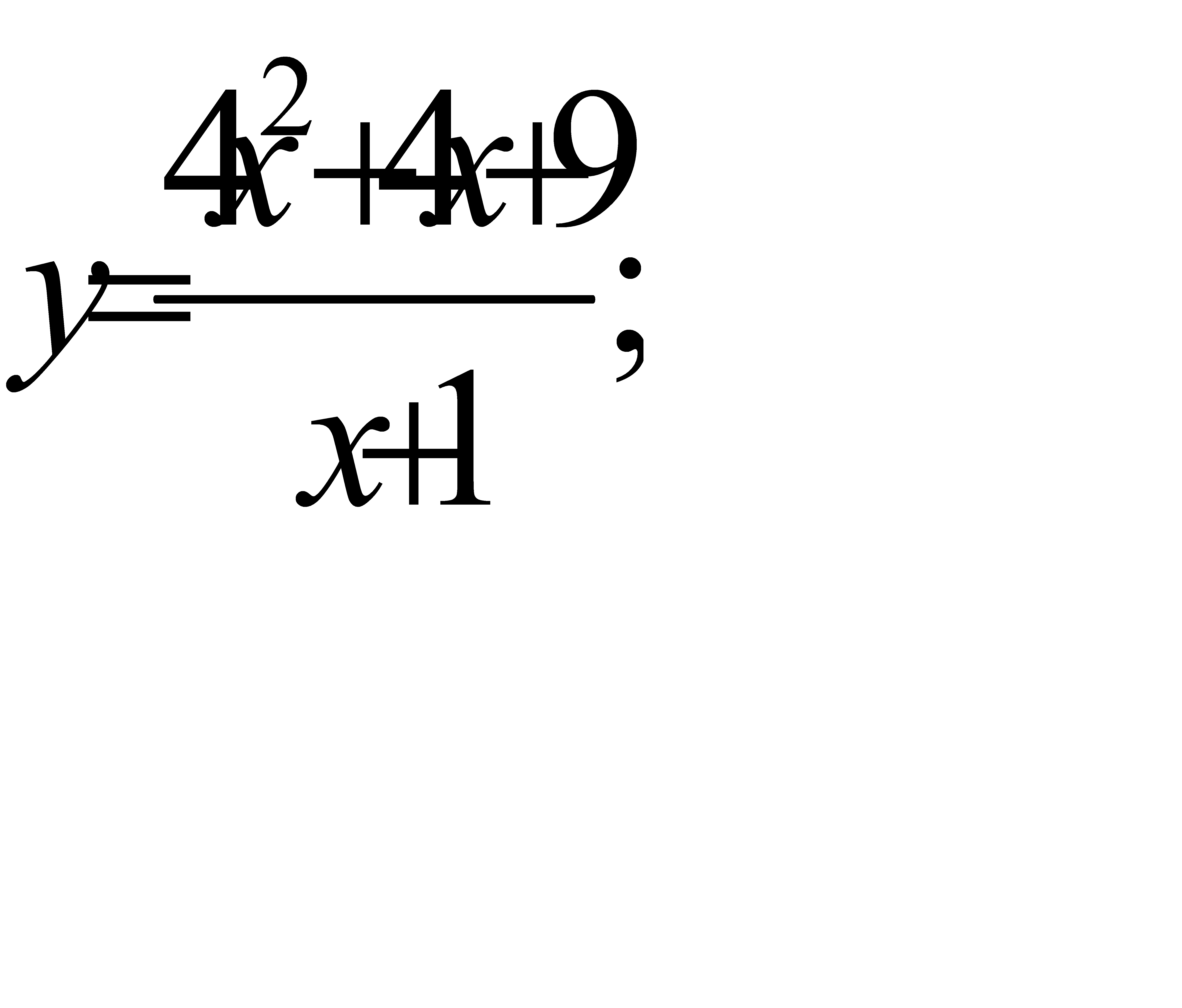
37. 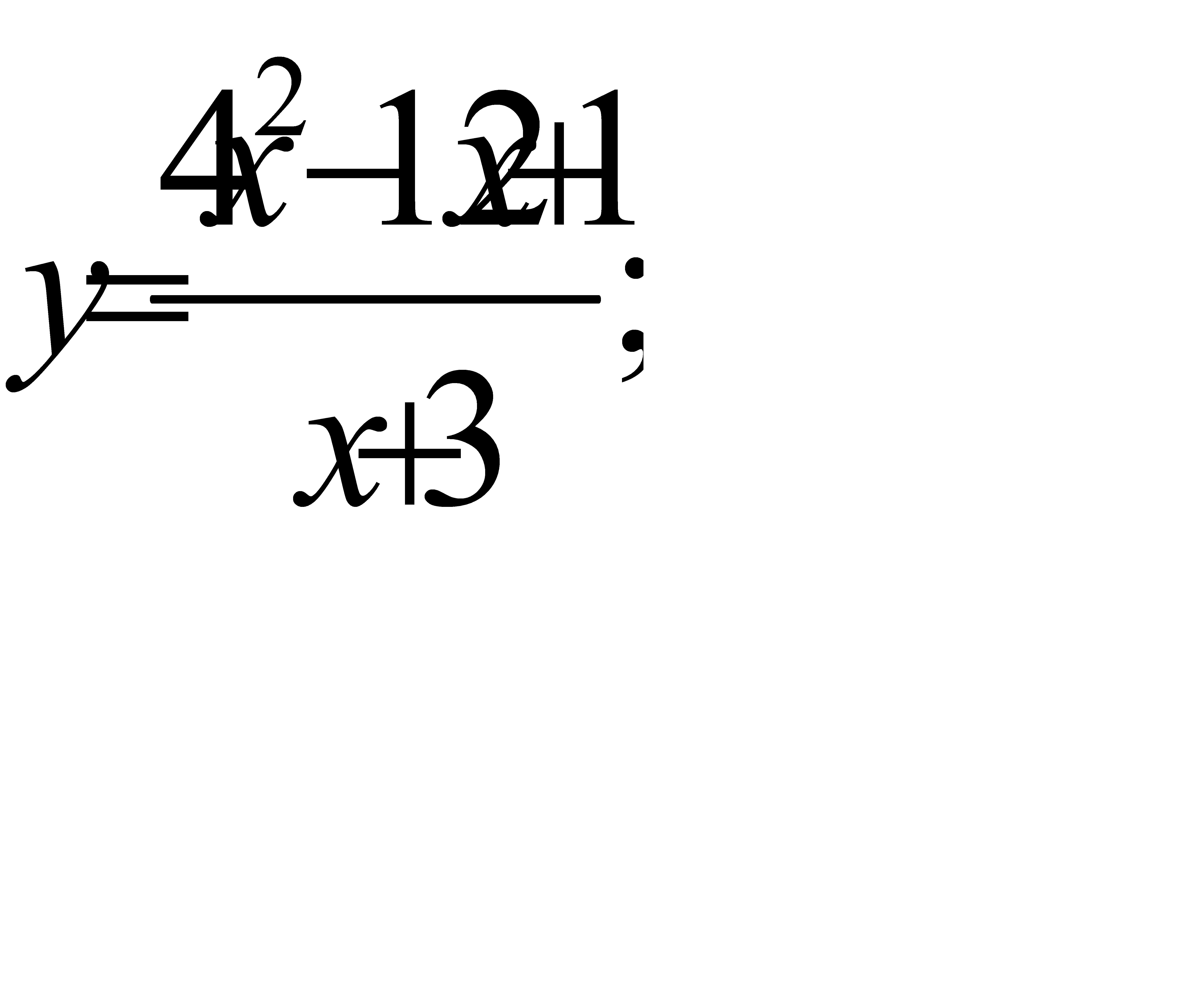 38.
38. 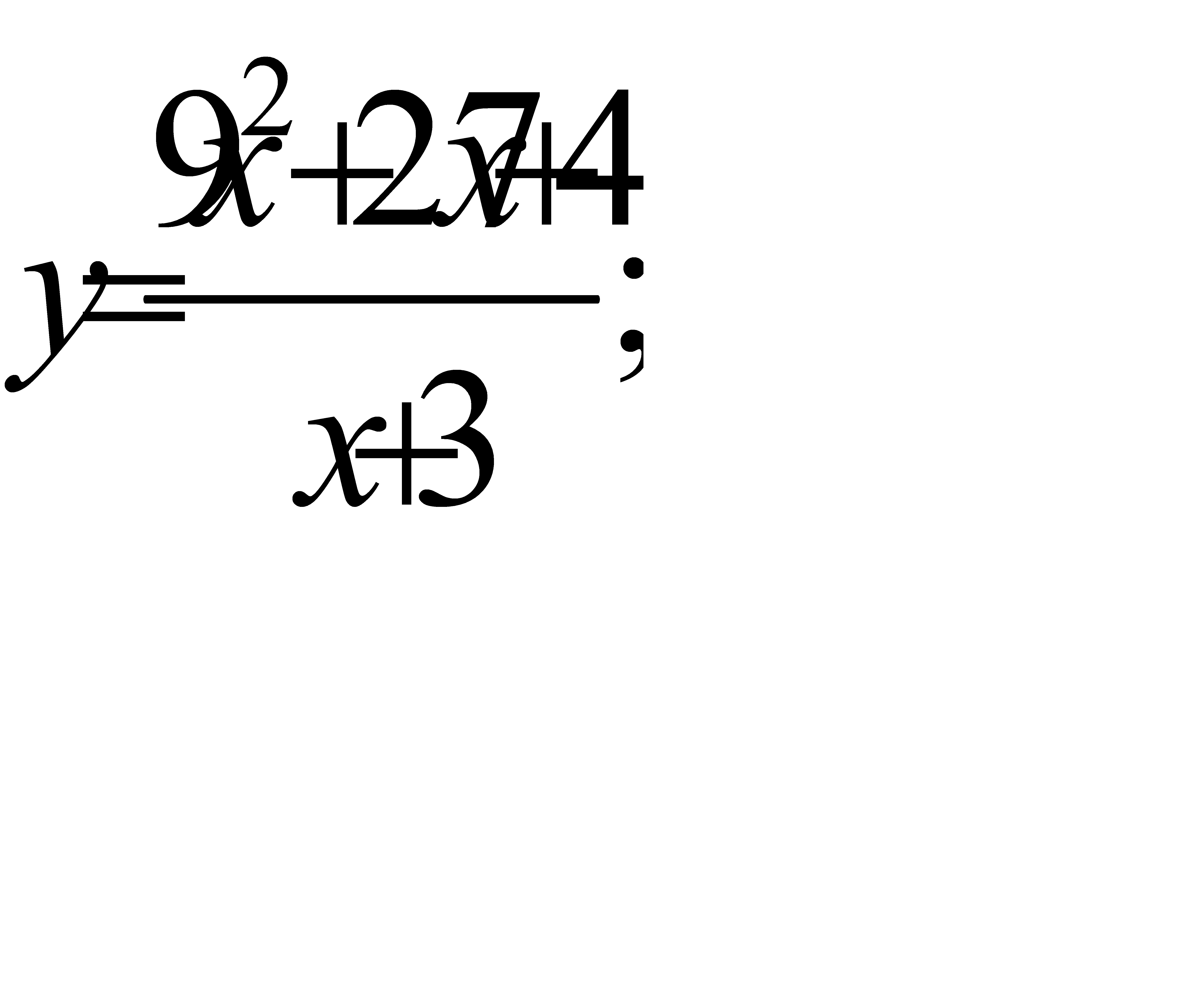
39. 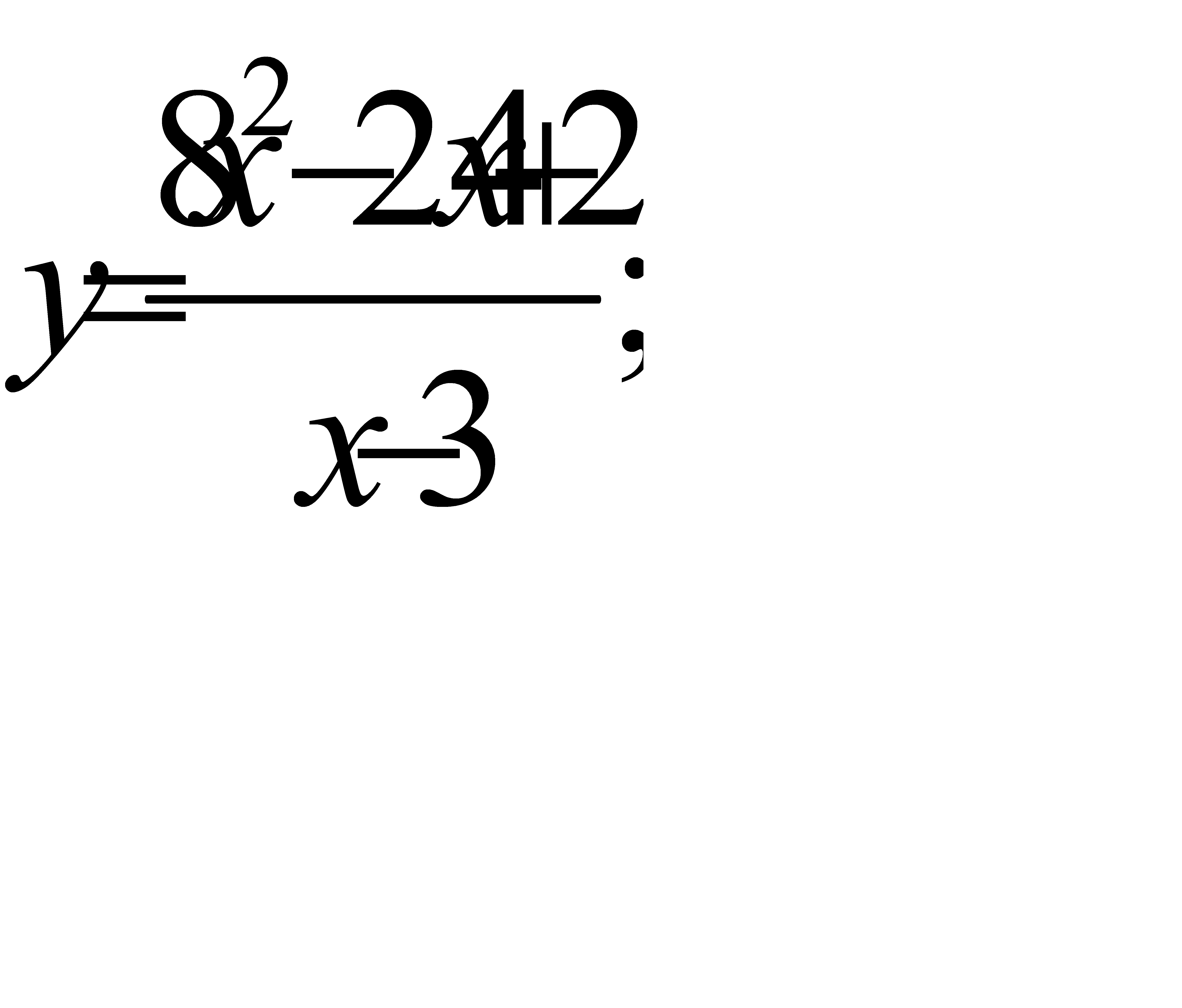 40.
40. 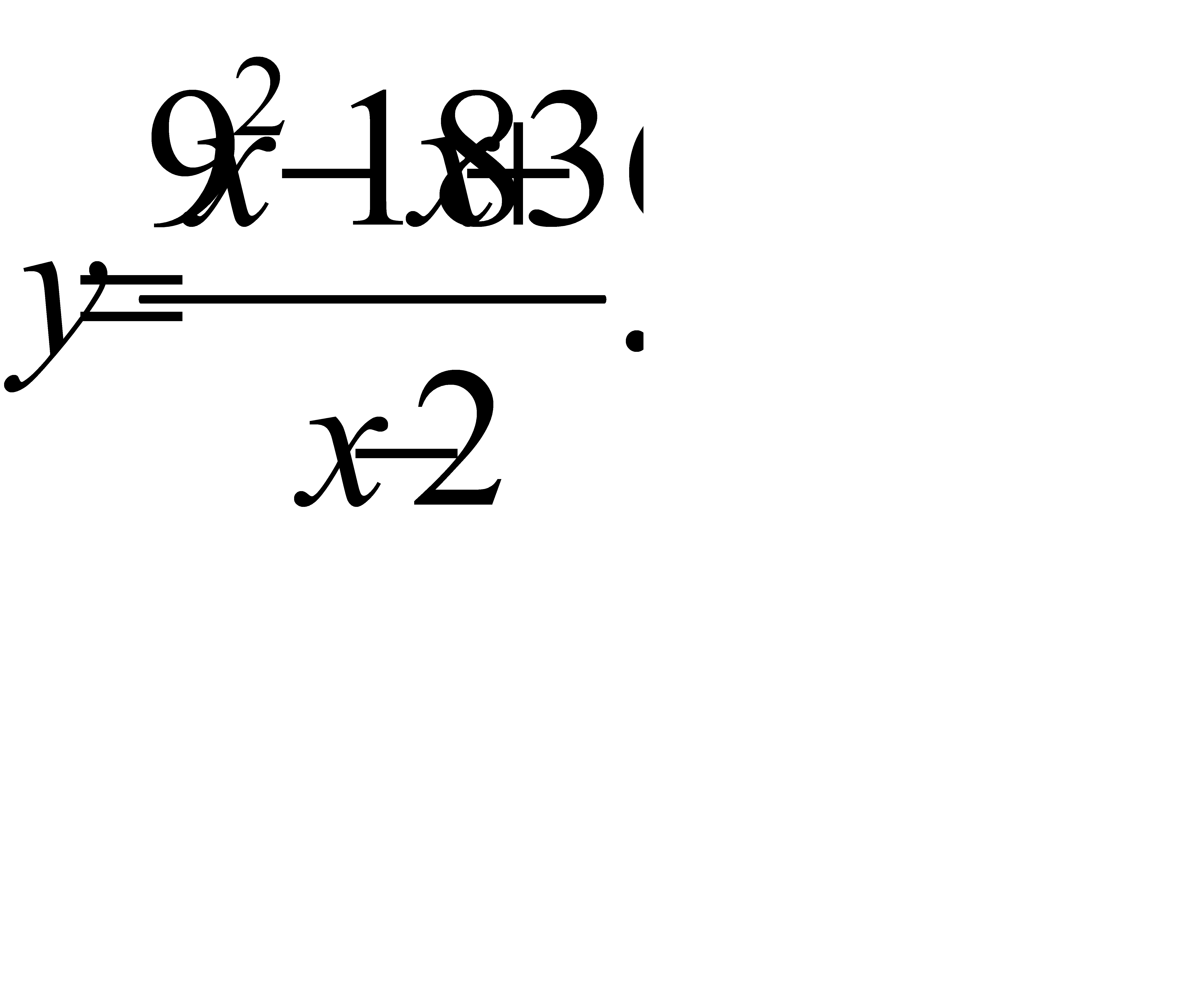
41-50. Найти неопределенные интегралы. Результаты проверить дифференцированием.
41. а) 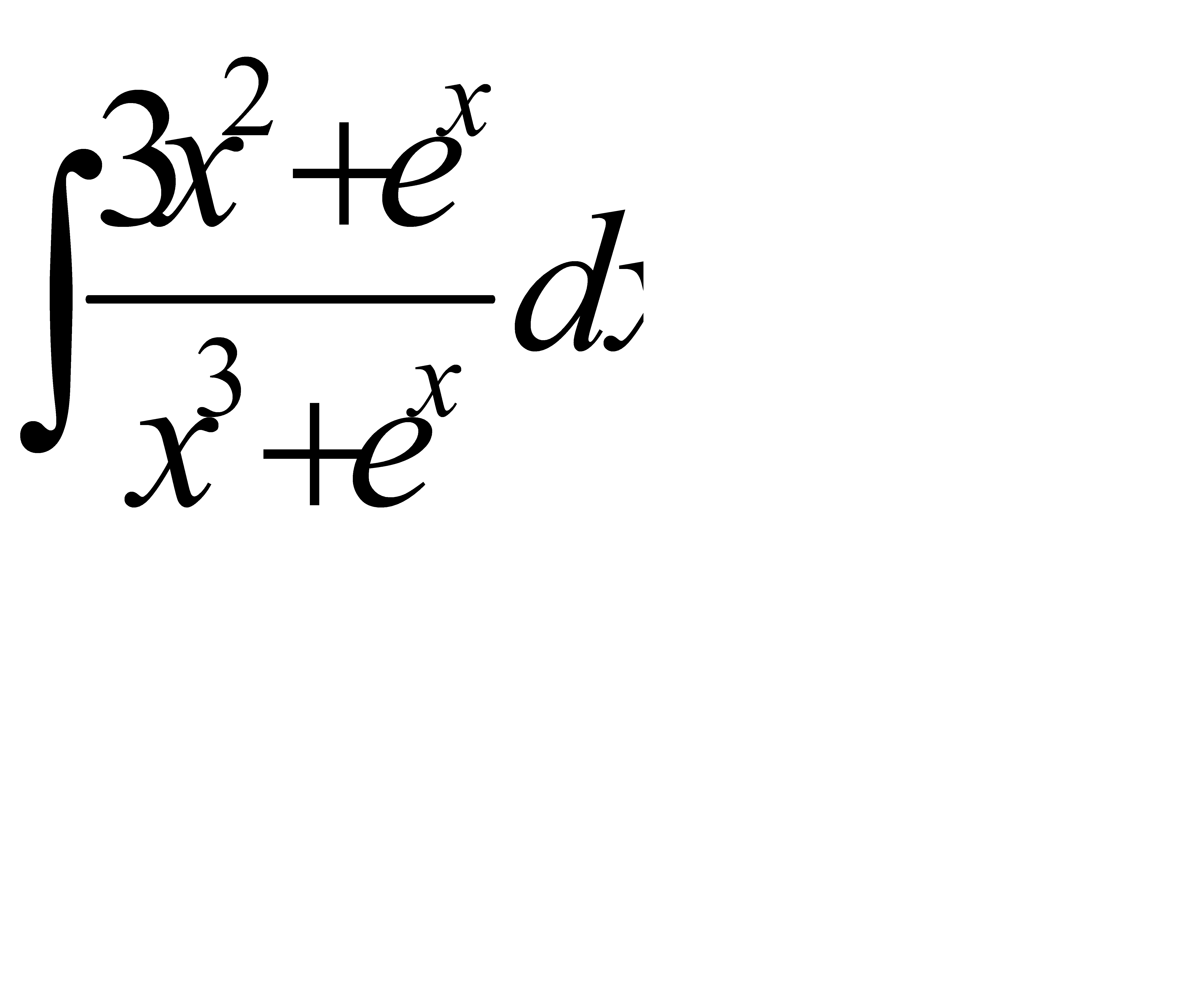 ; б)
; б) 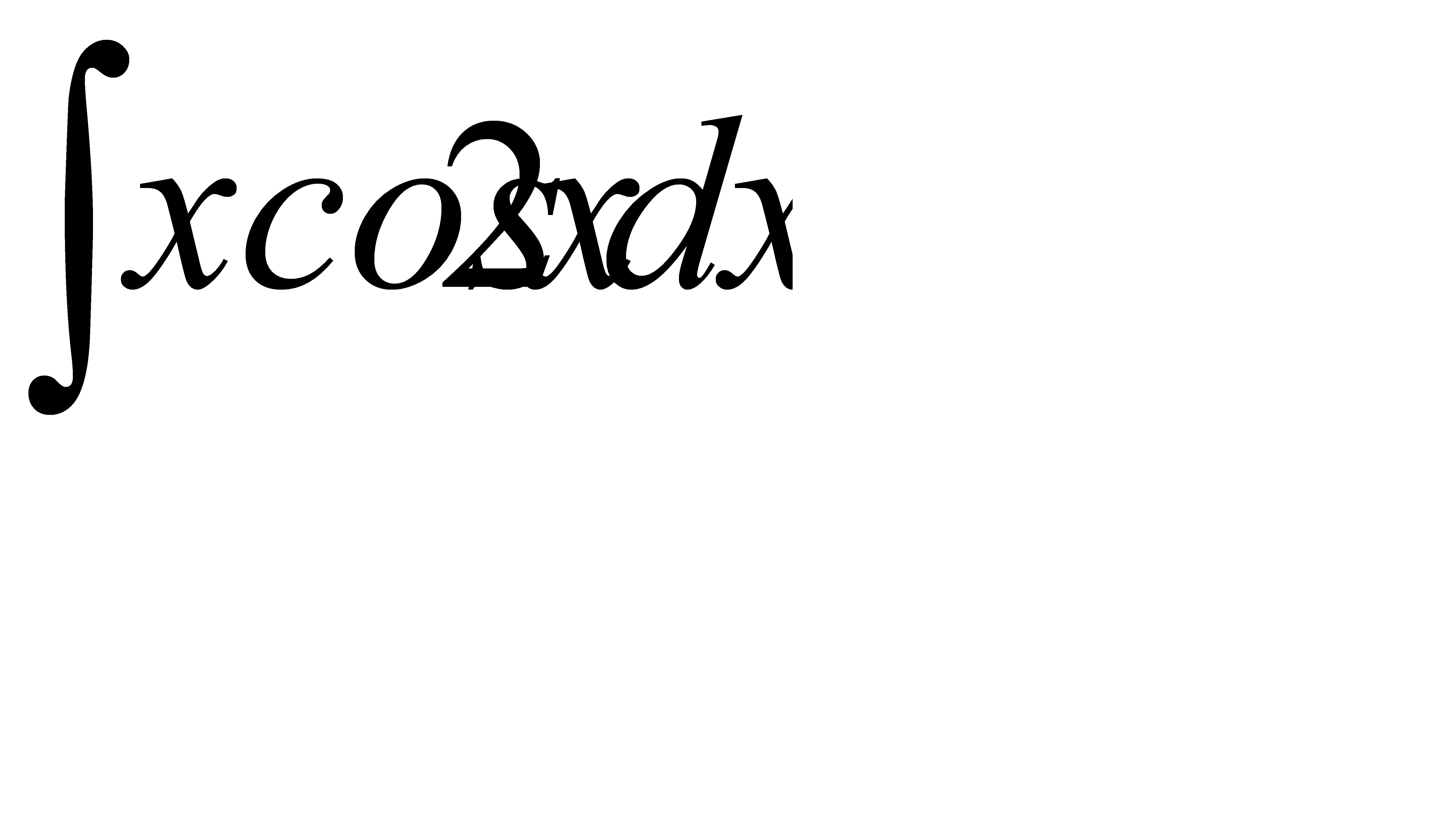 ;
;
42. а) 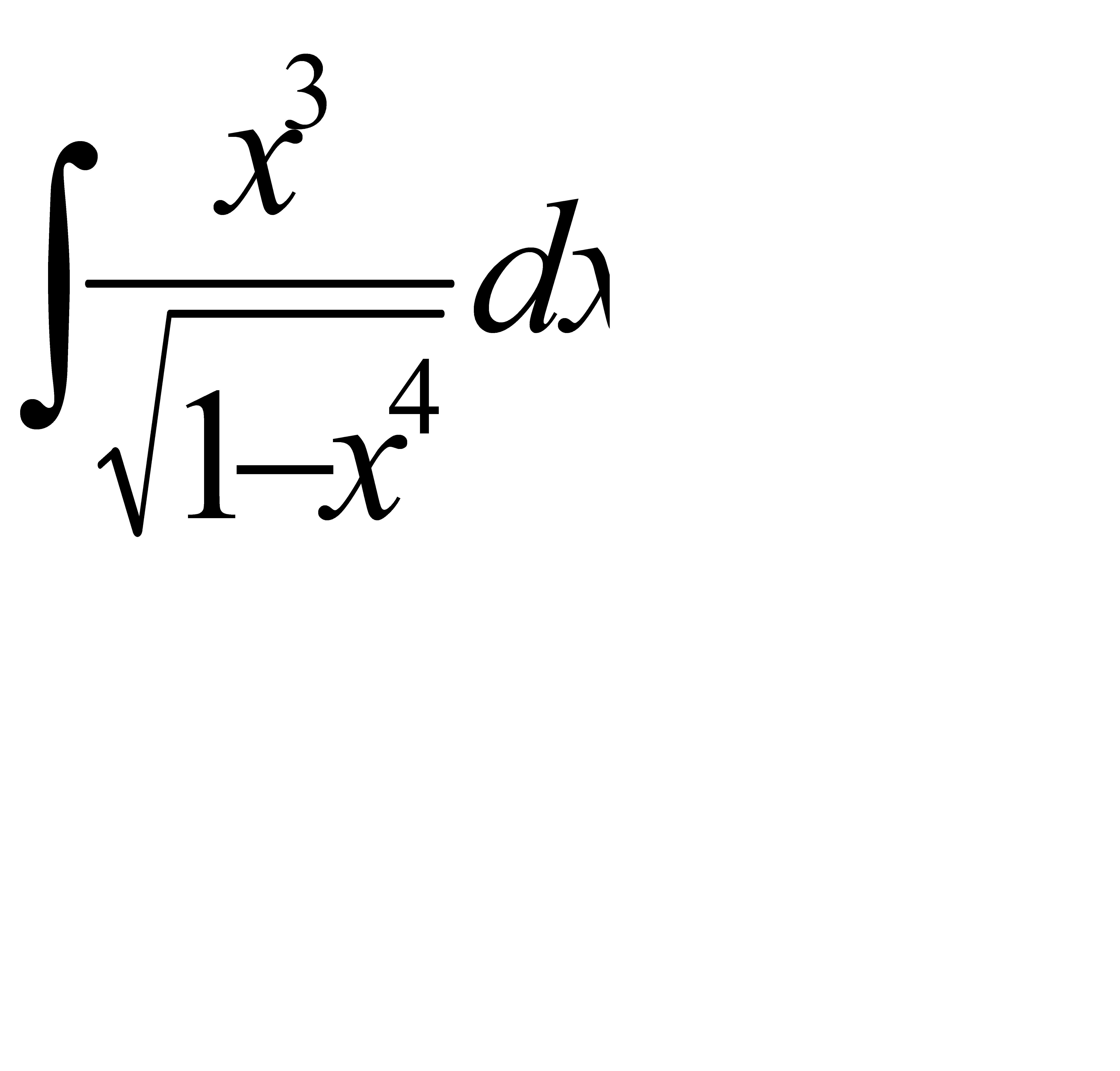 ; б)
; б) 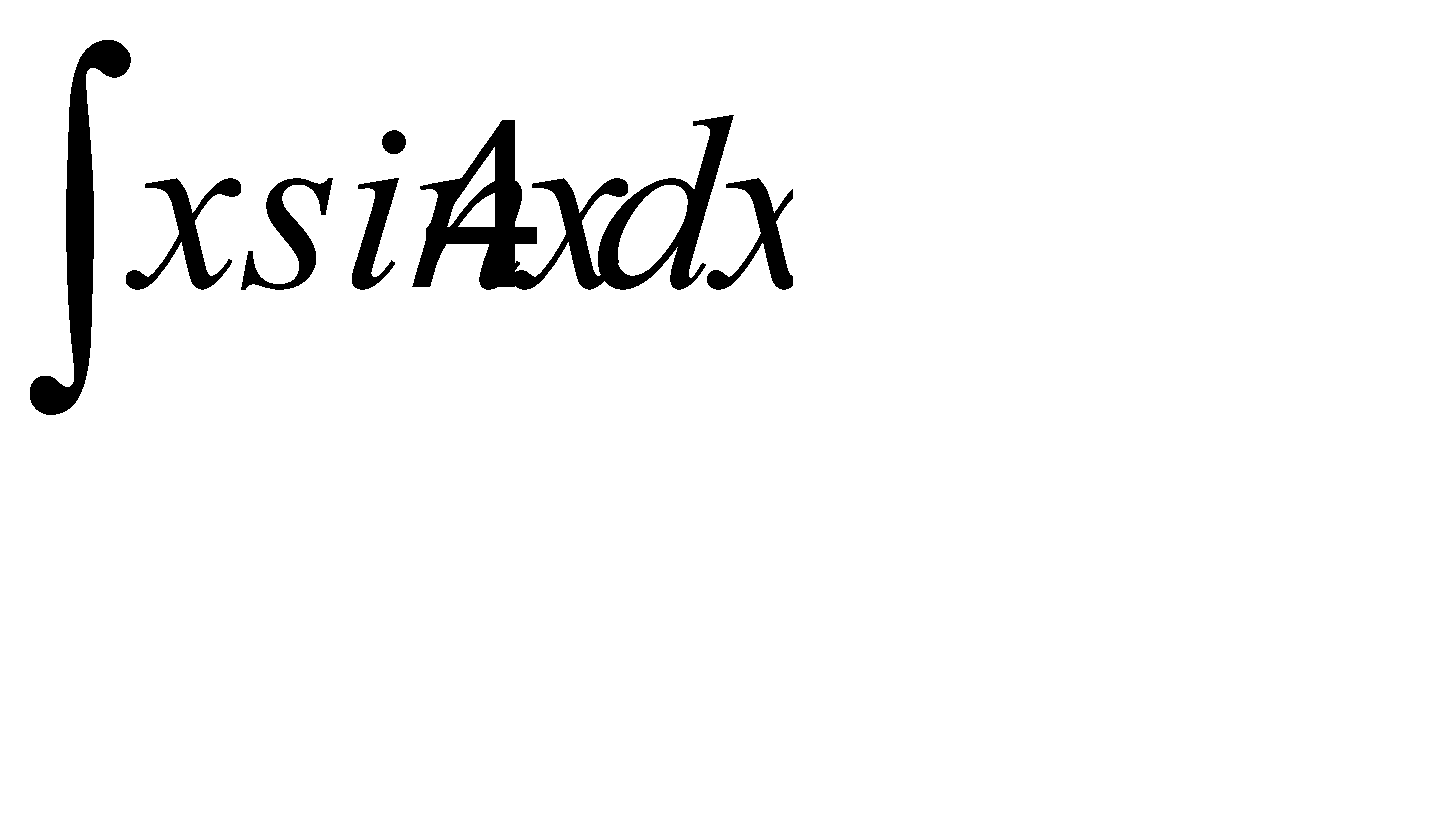 ;
;
- а)
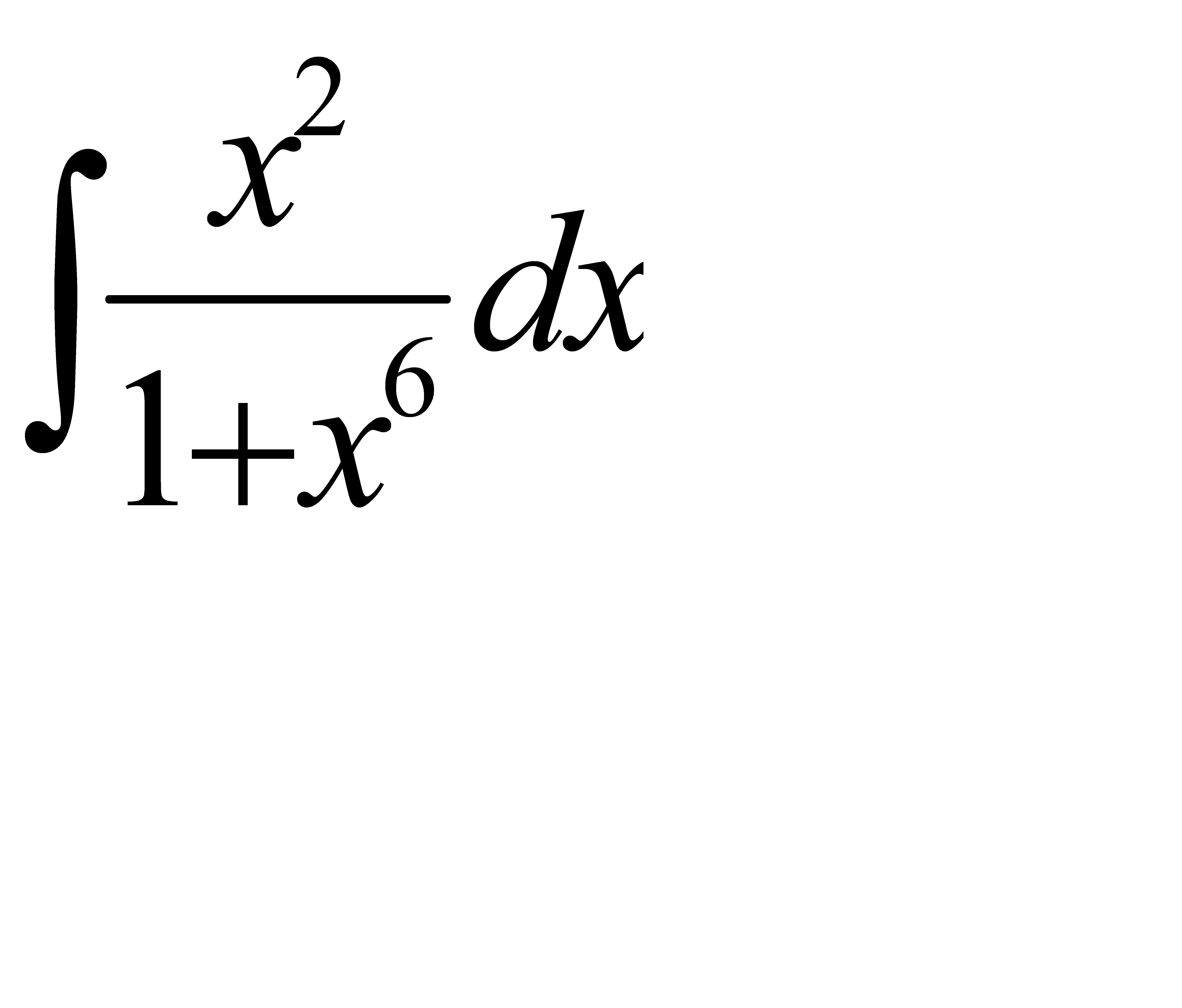 ; б)
; б) 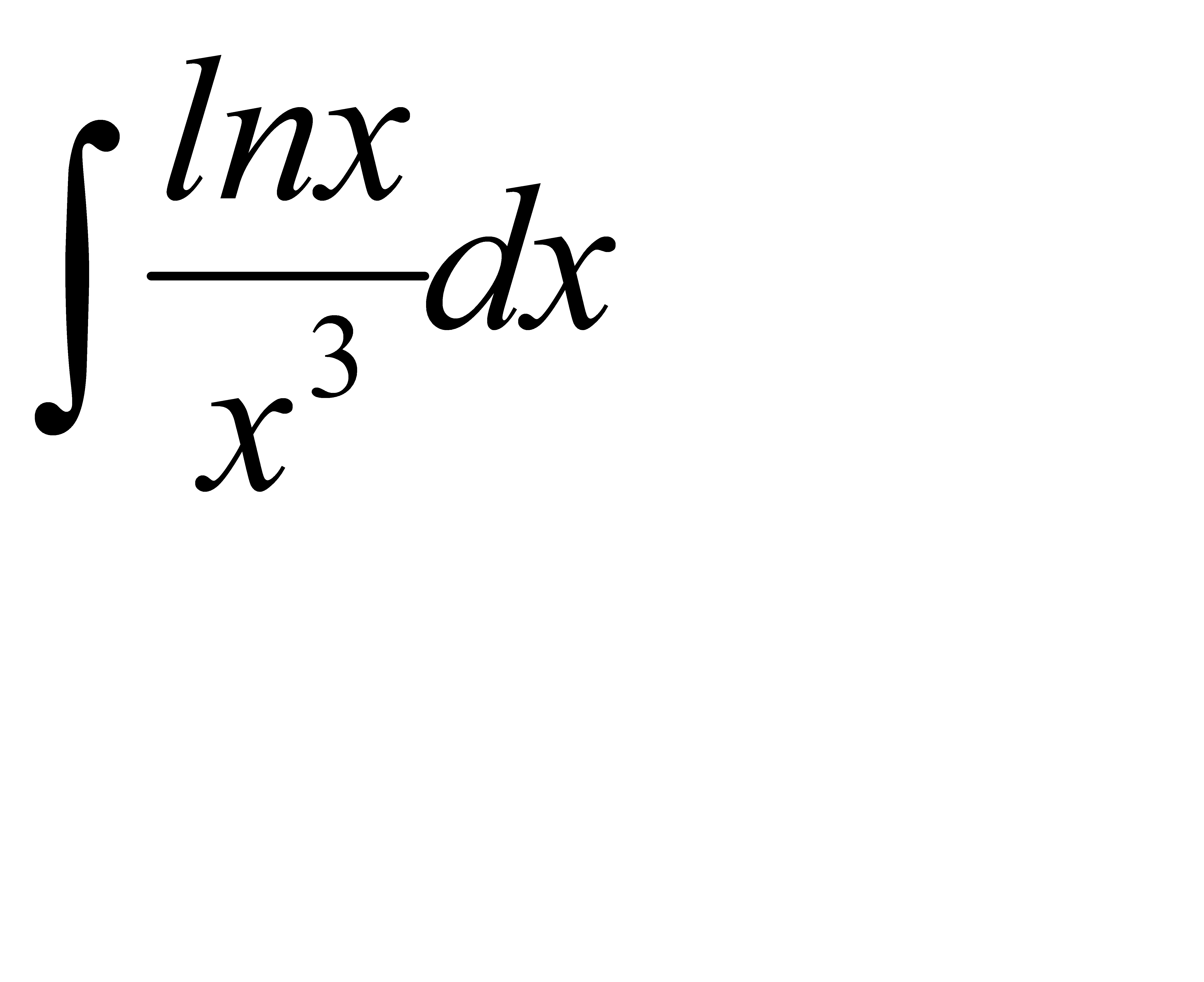 ;
; - а)
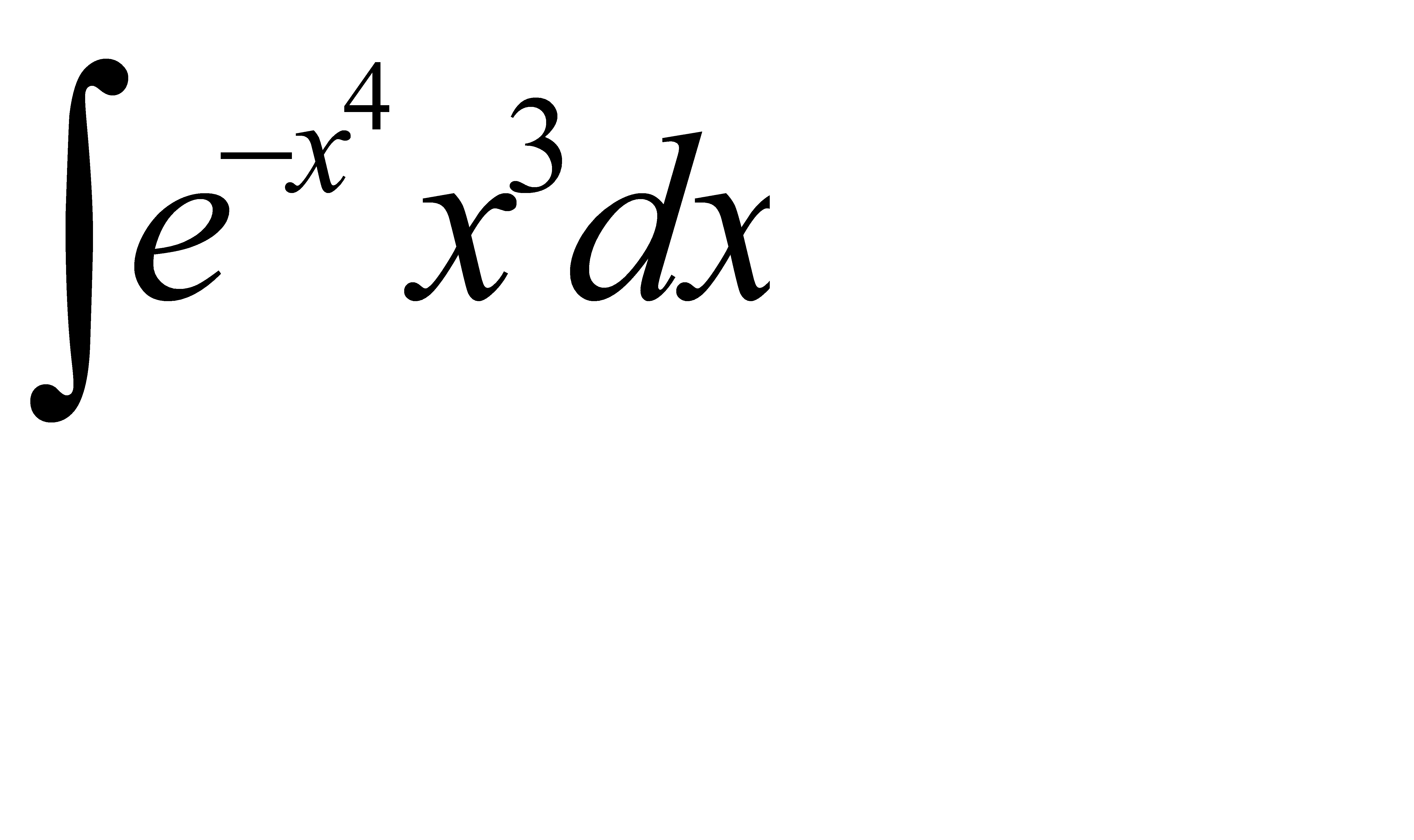 ; б)
; б) 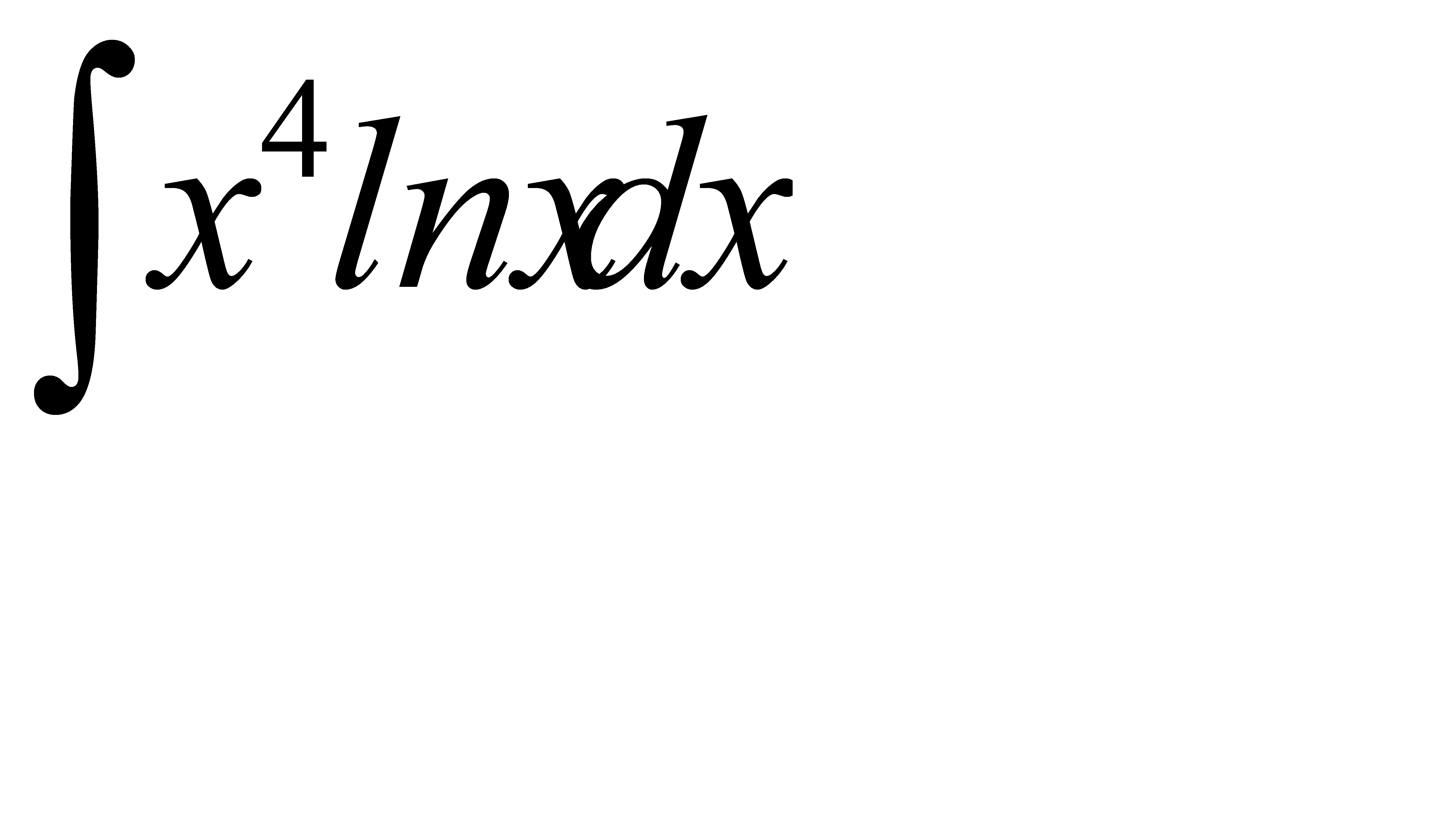 ;
;
45. а) 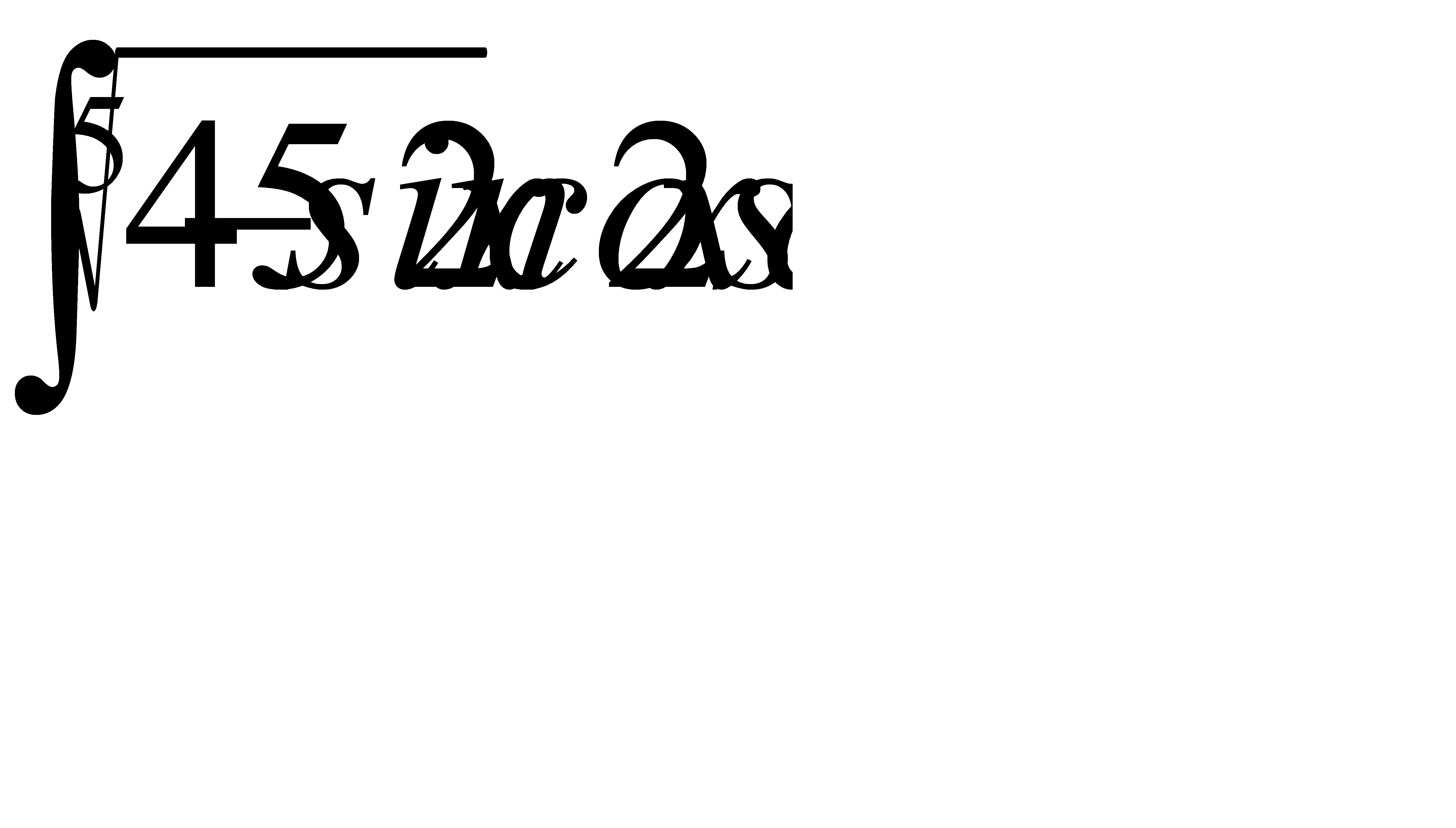 ; б)
; б) 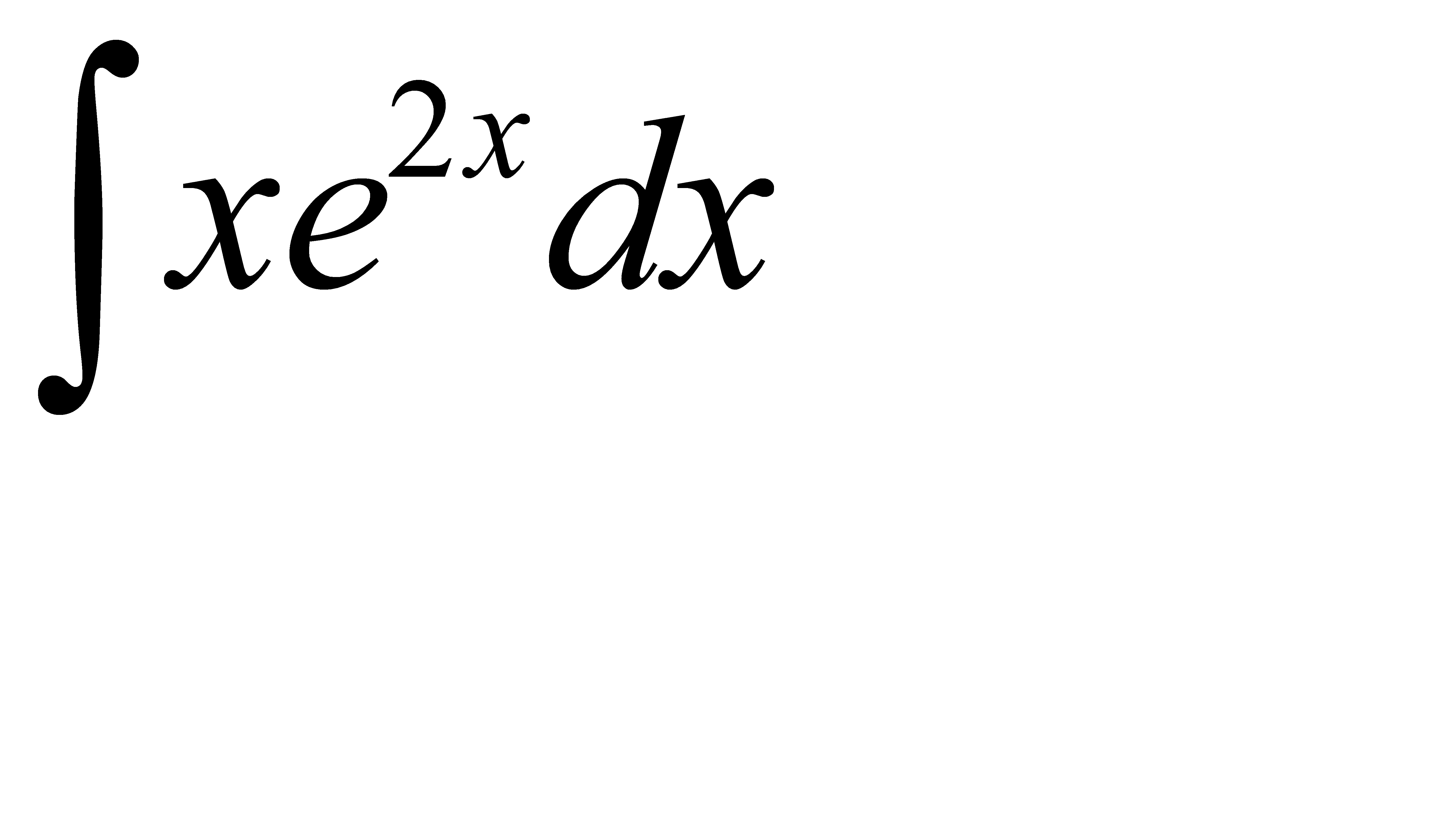 ;
;
46. а) 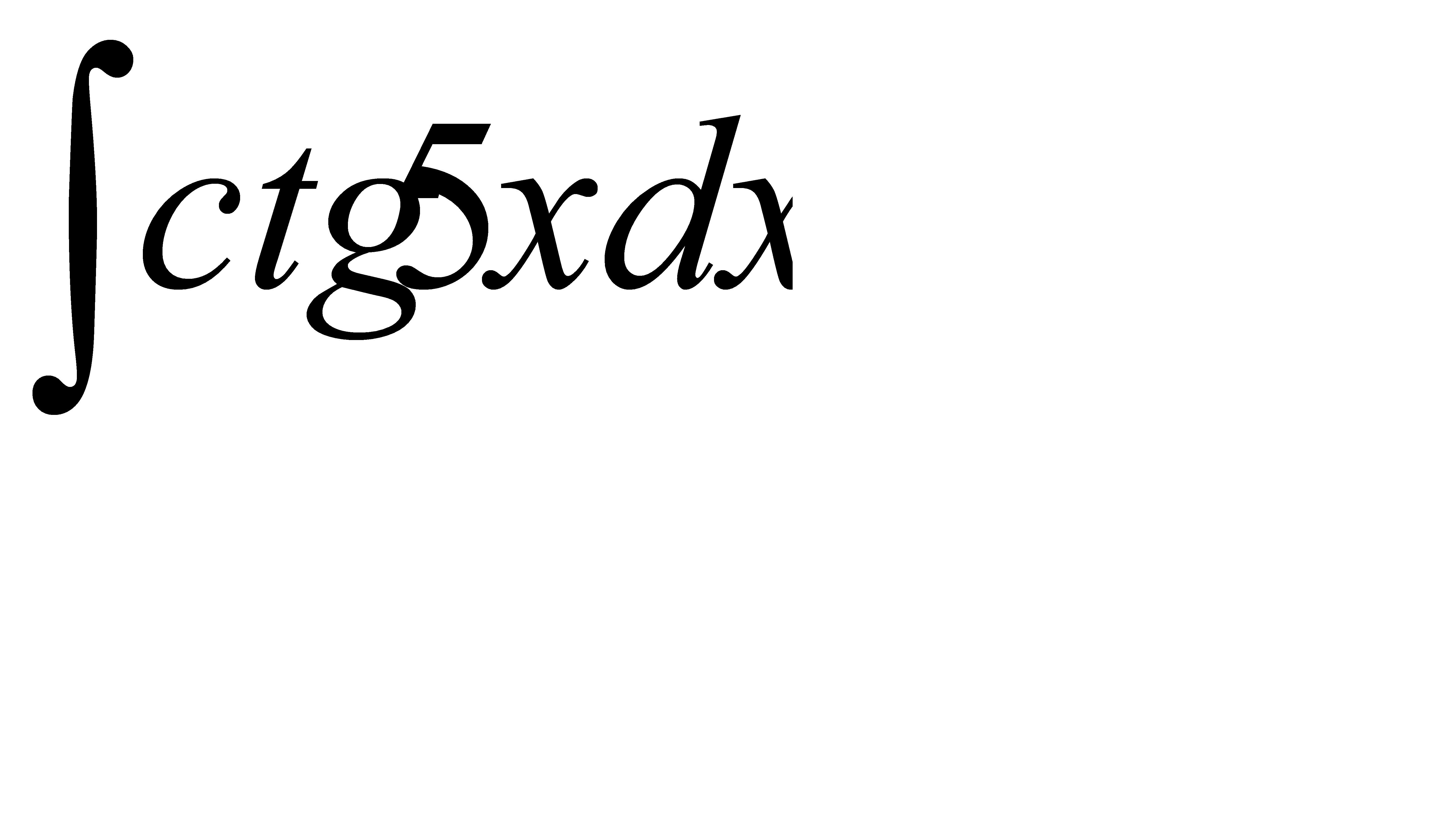 ; б)
; б) 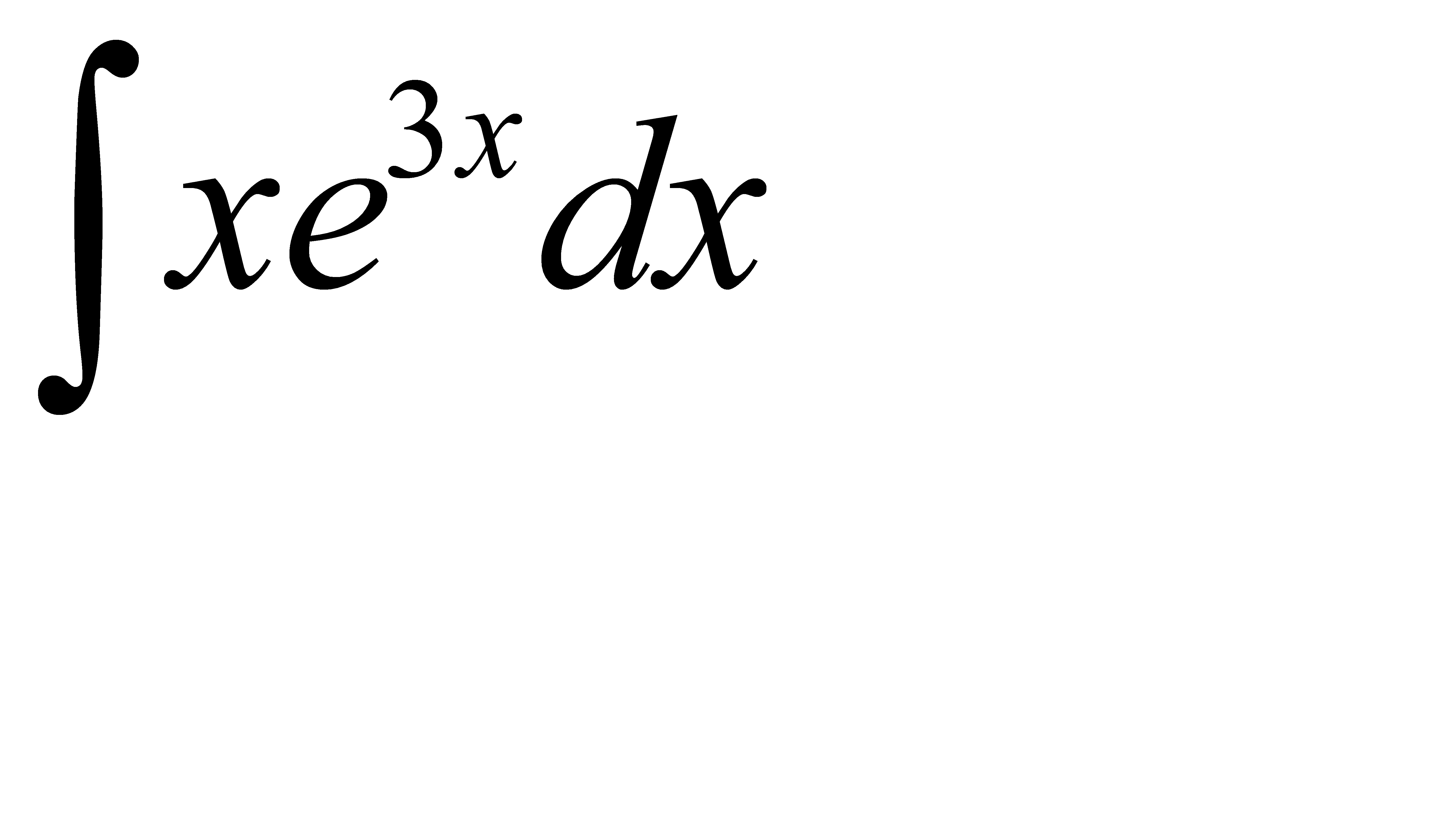 ;
;
47. а) 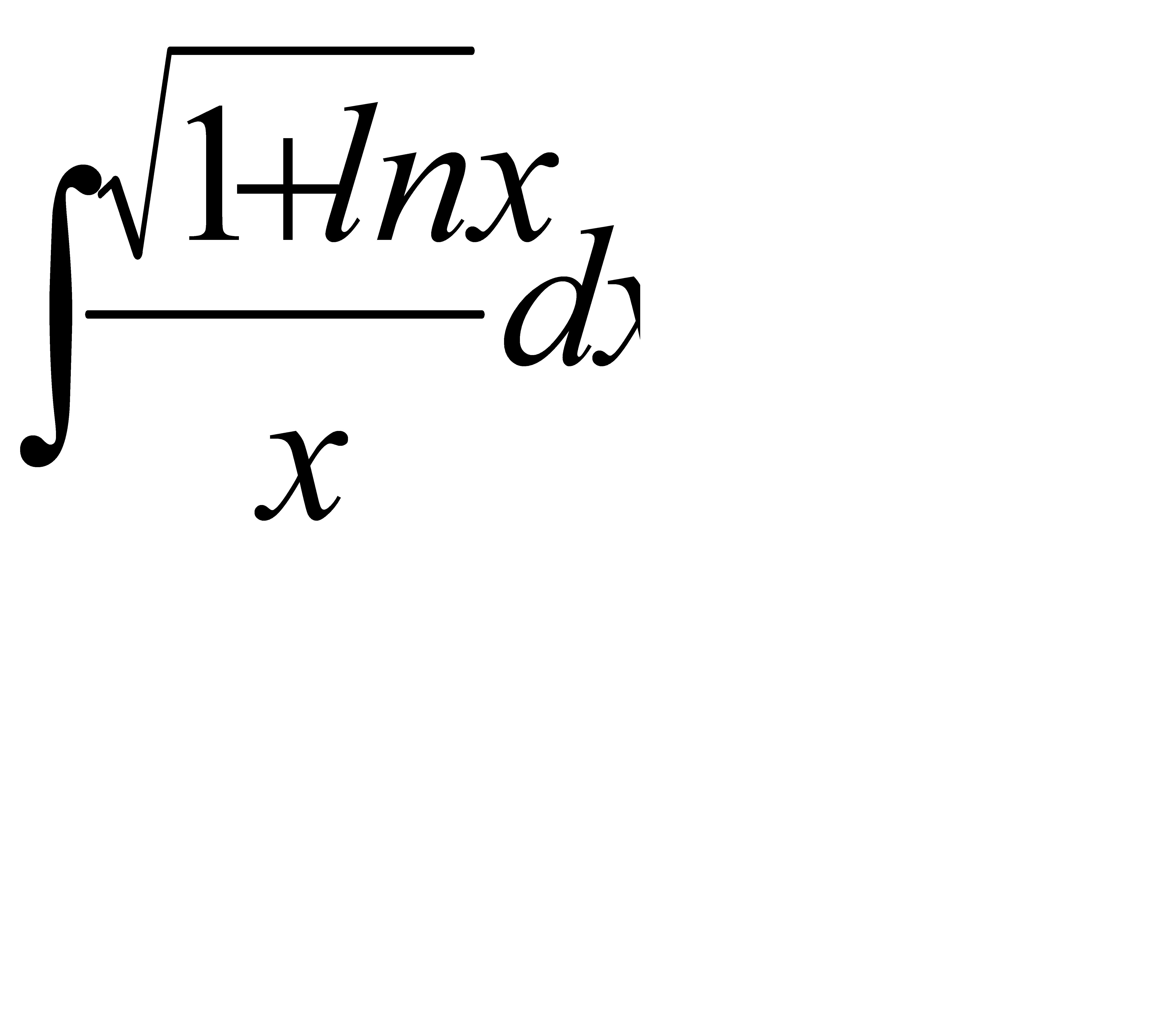 ; б)
; б) 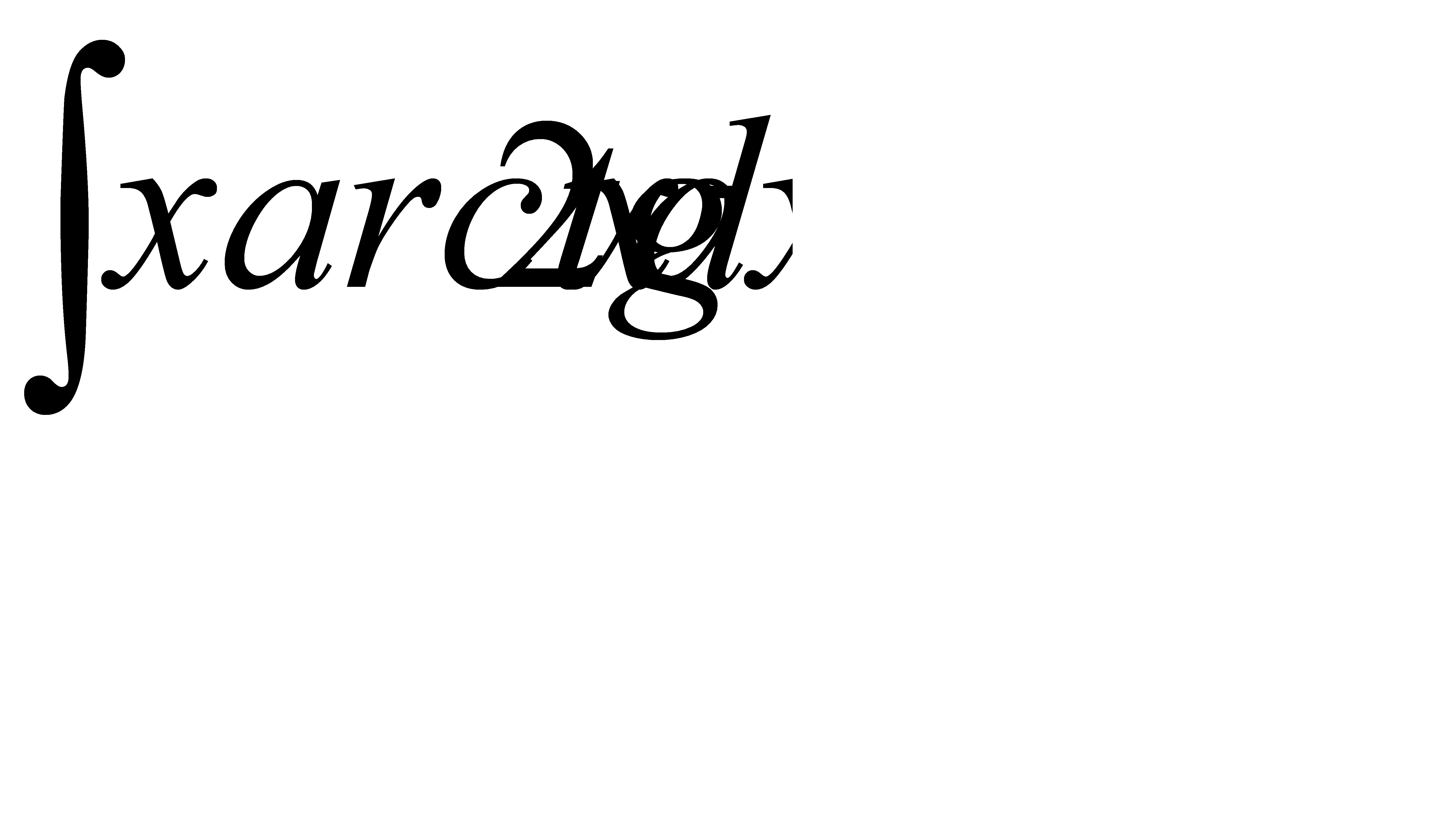 ;
;
48. а) 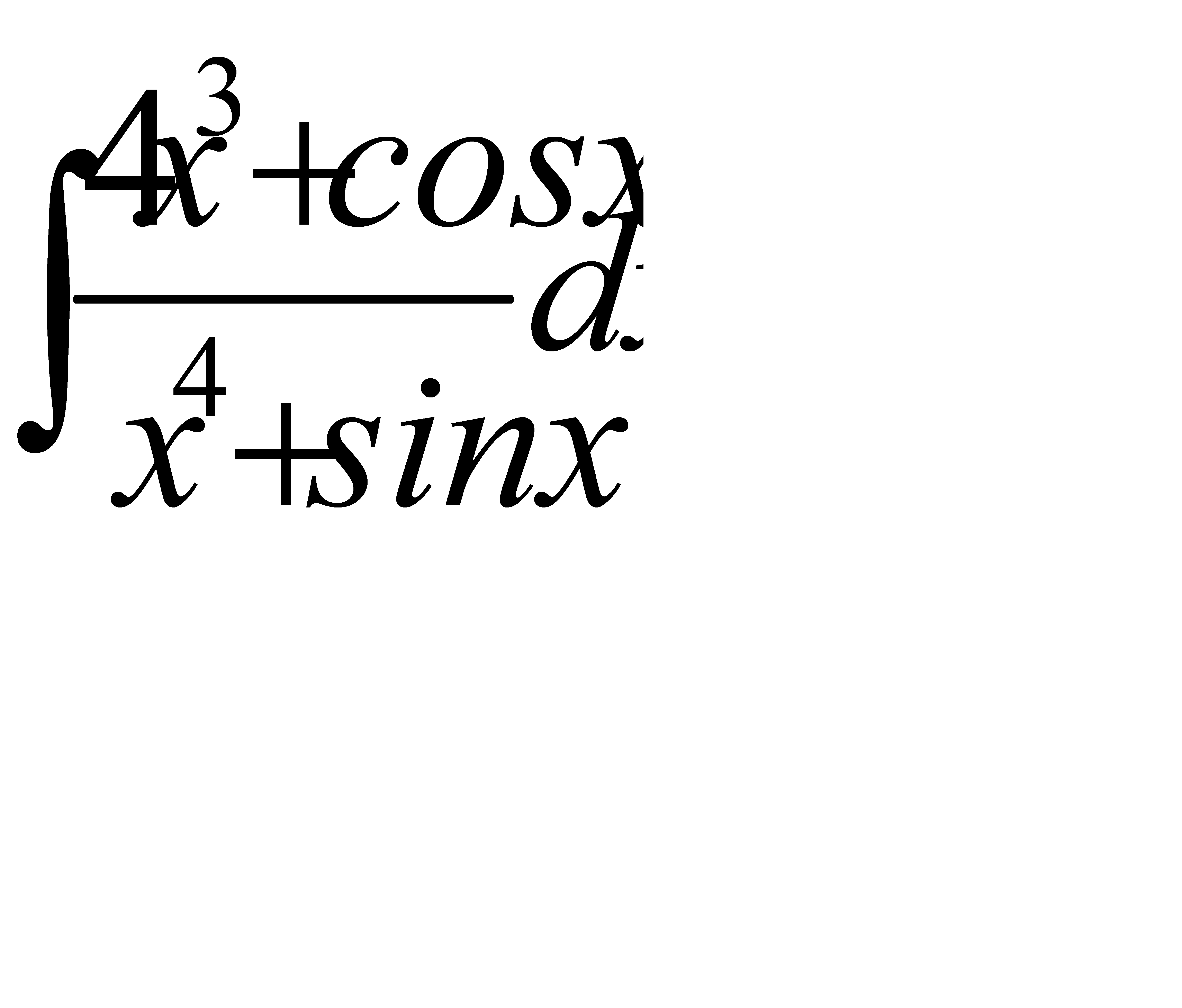 ; б)
; б) 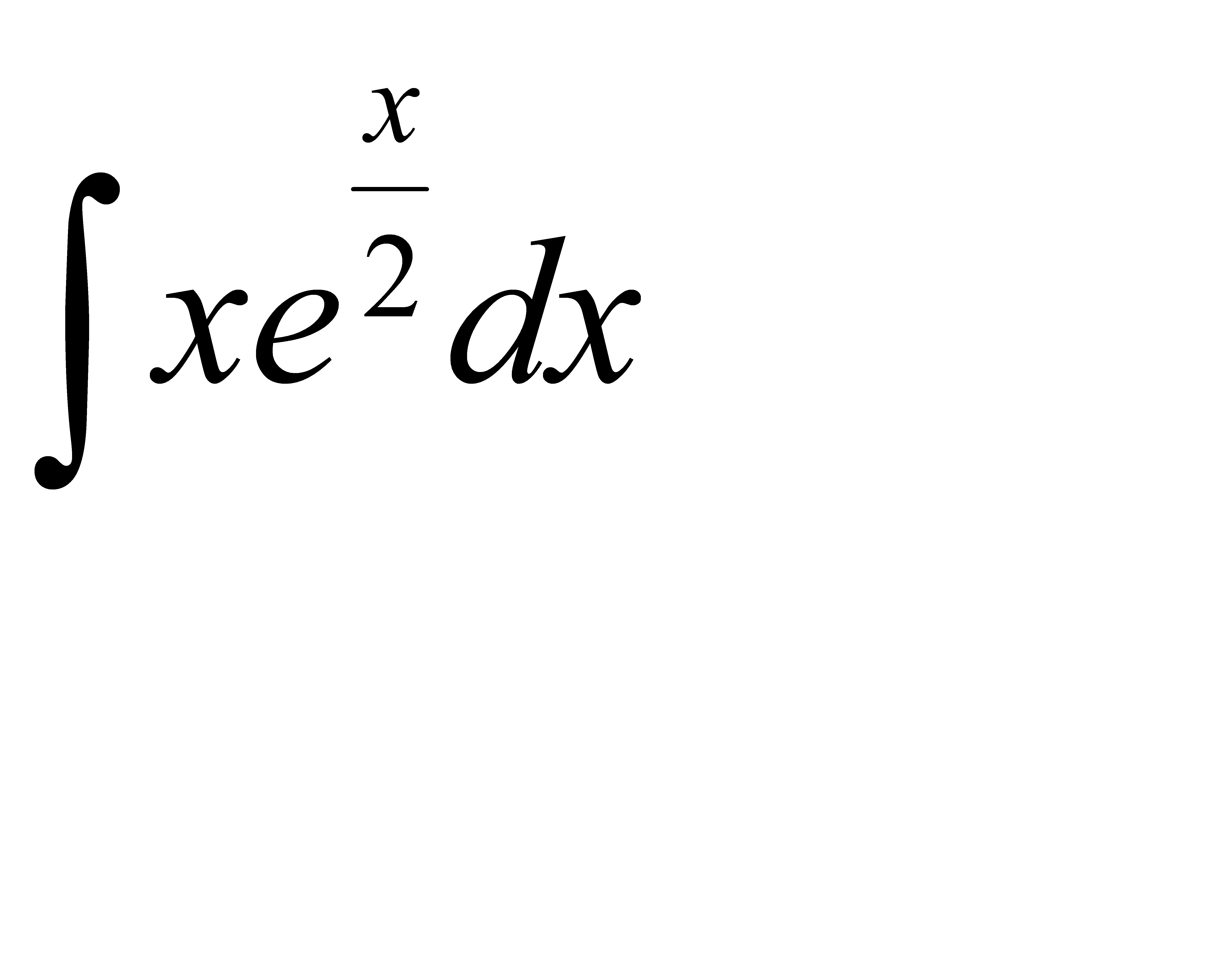 ;
;
49. а) 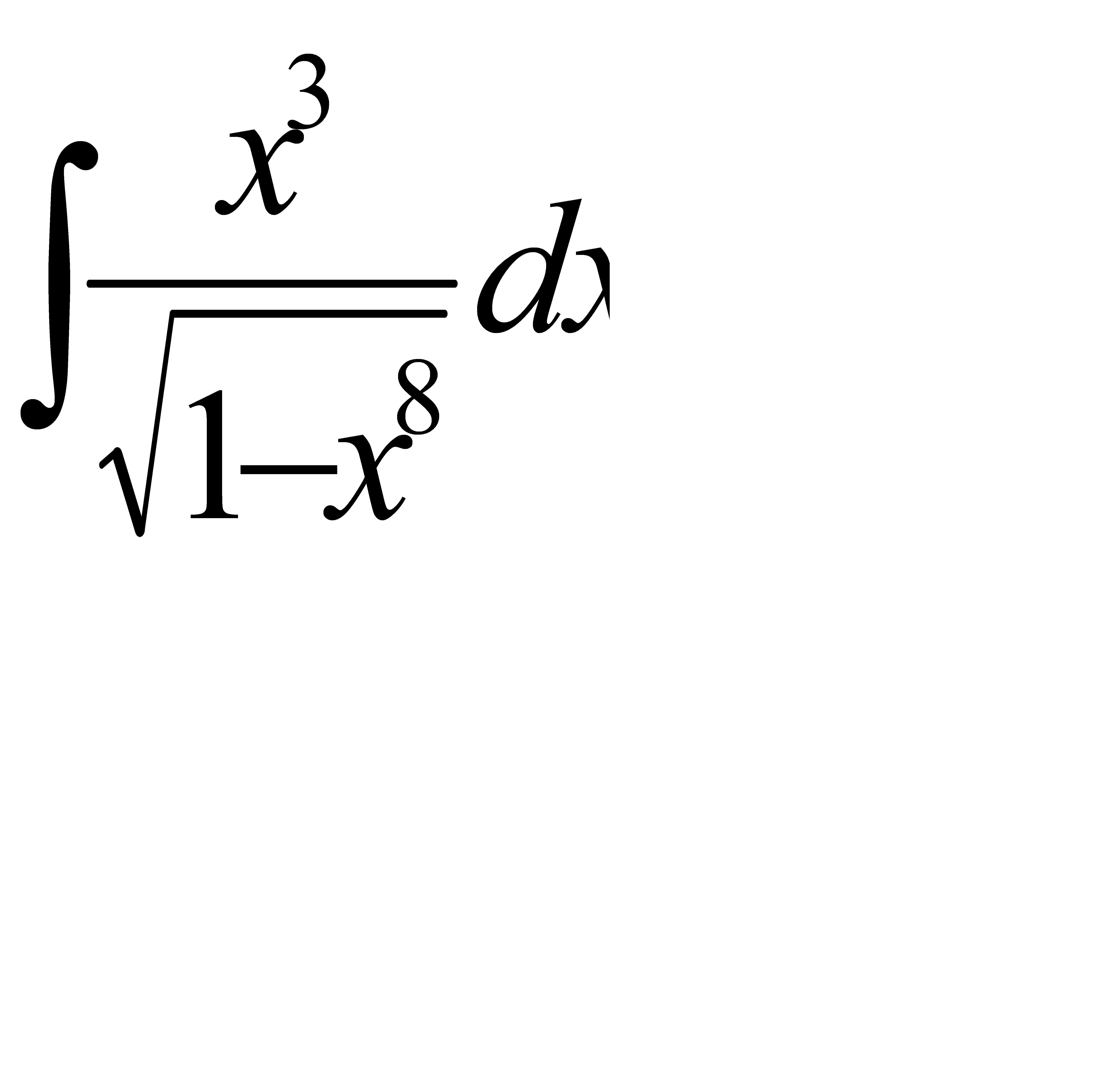 ; б)
; б) 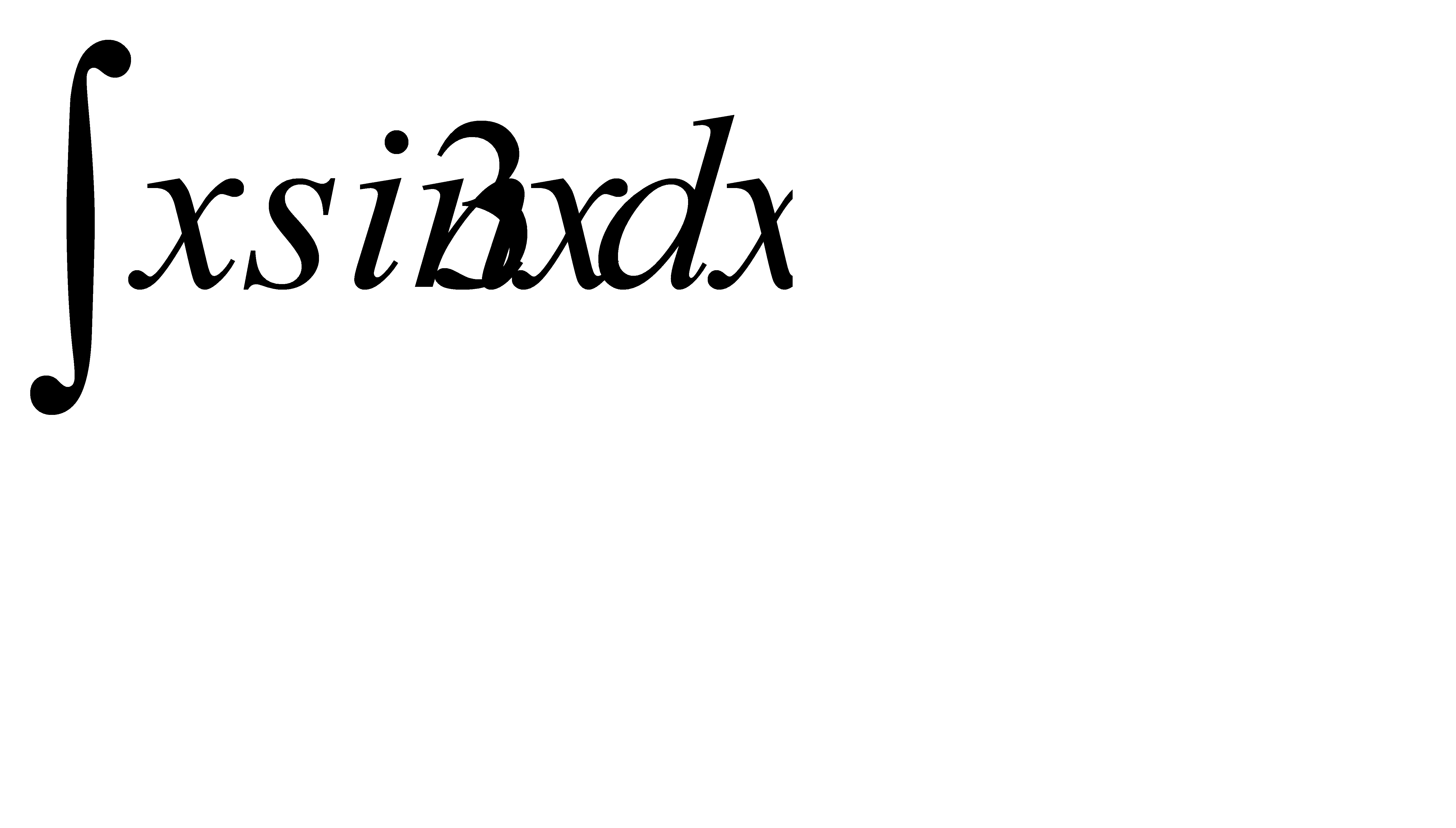 ;
;
50. а) 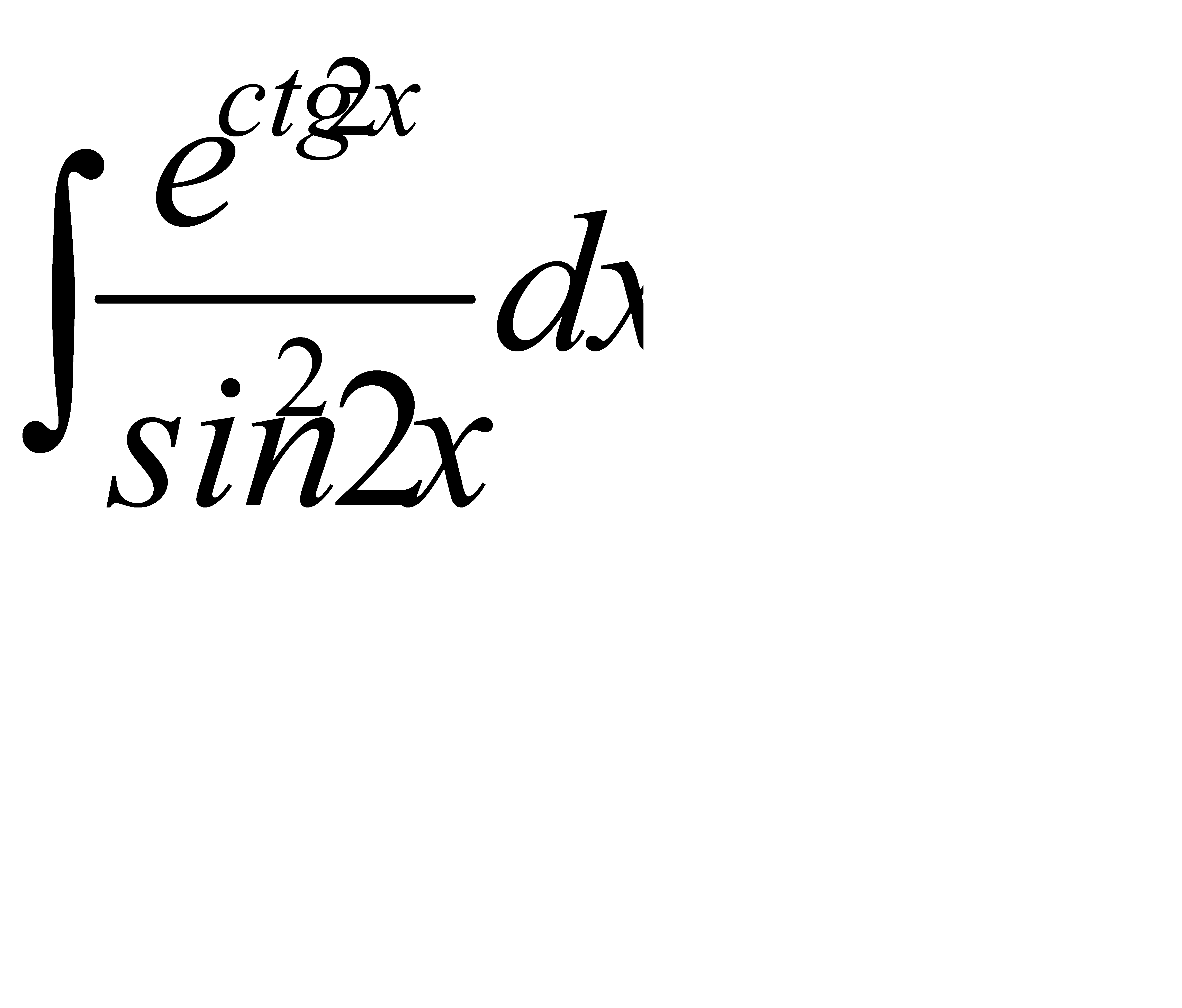 ; б)
; б) 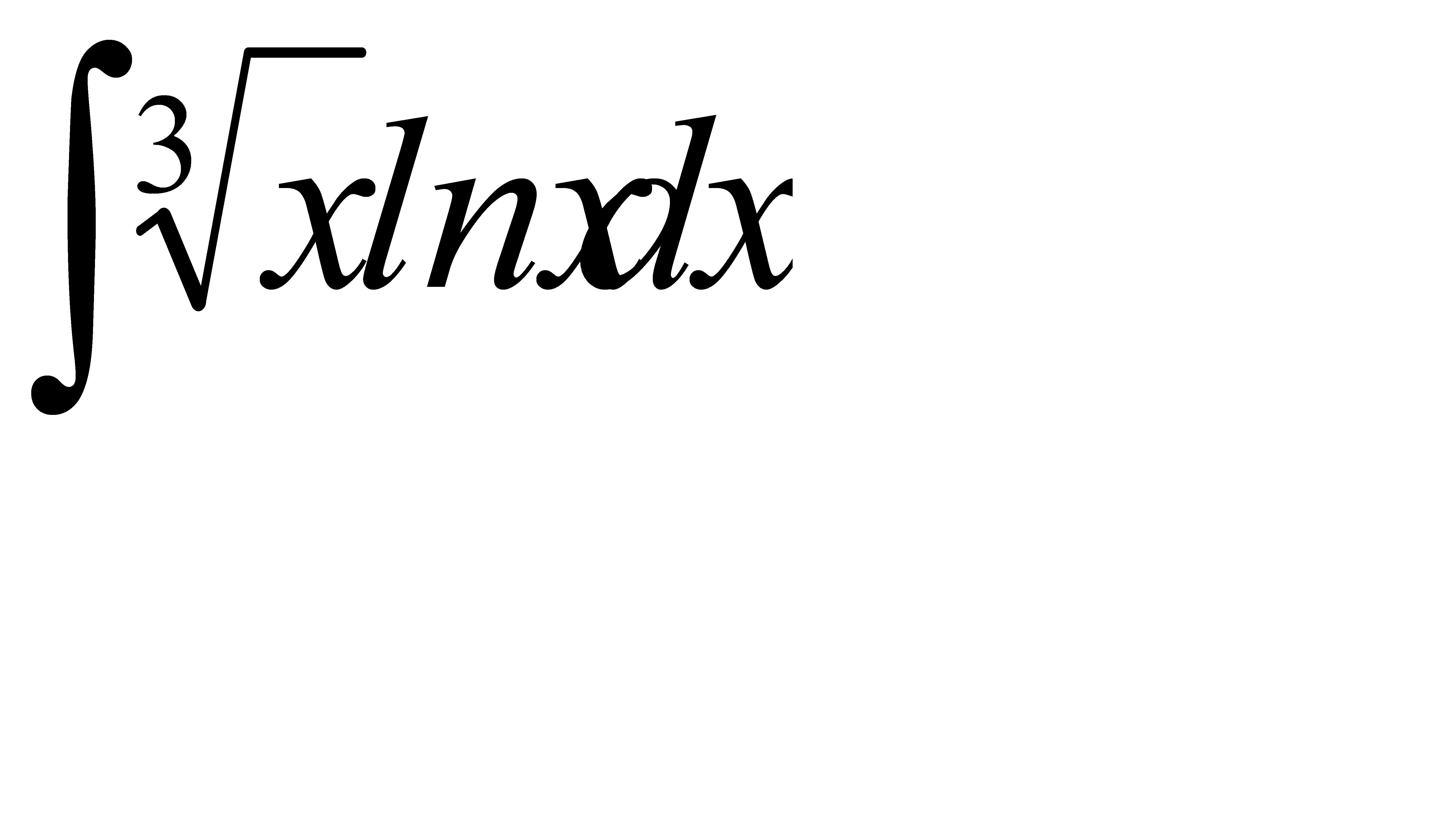 .
.
51-60. Вычислить по формуле Ньютона-Лейбница определенный интеграл 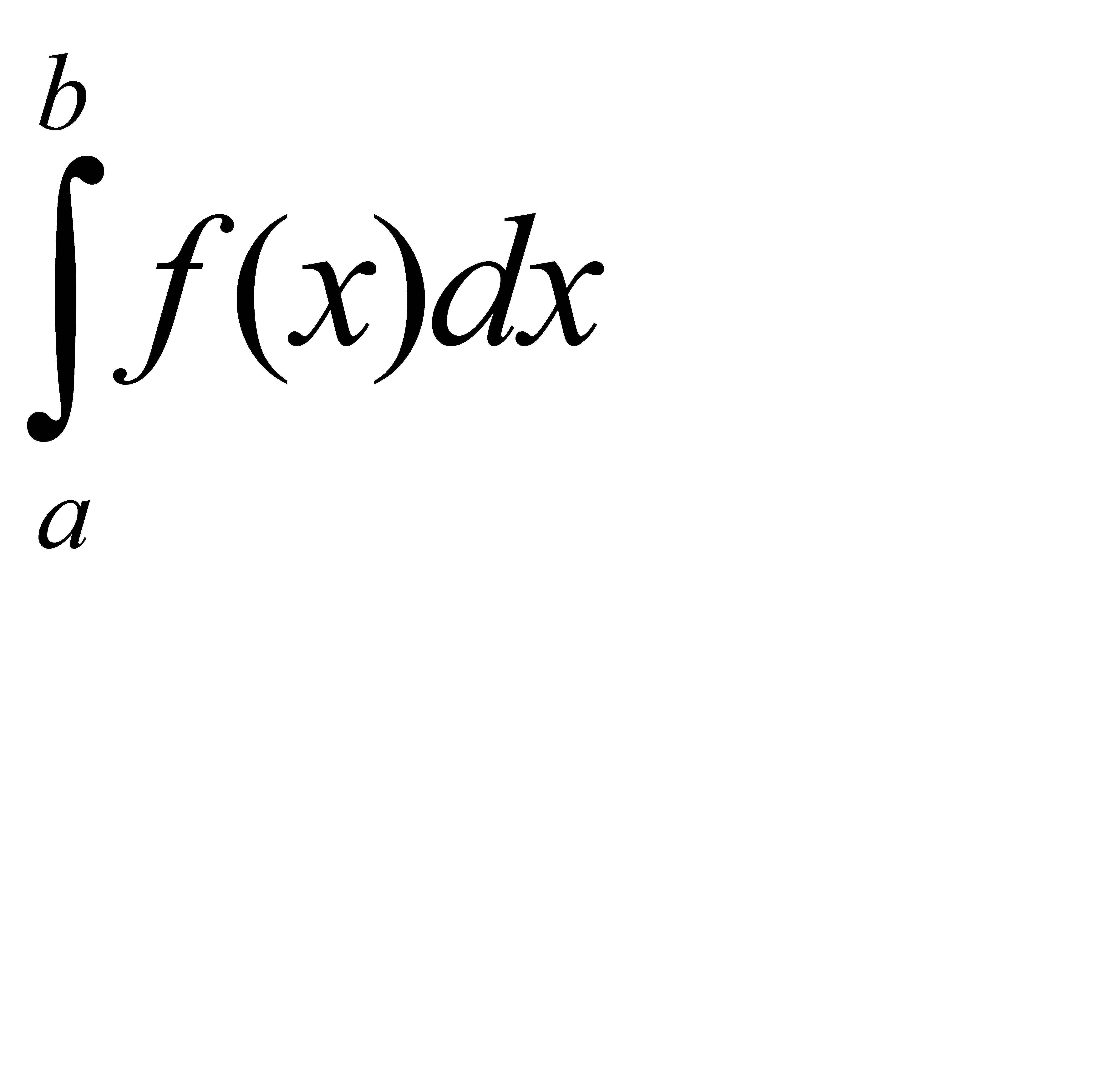 .
.
51. 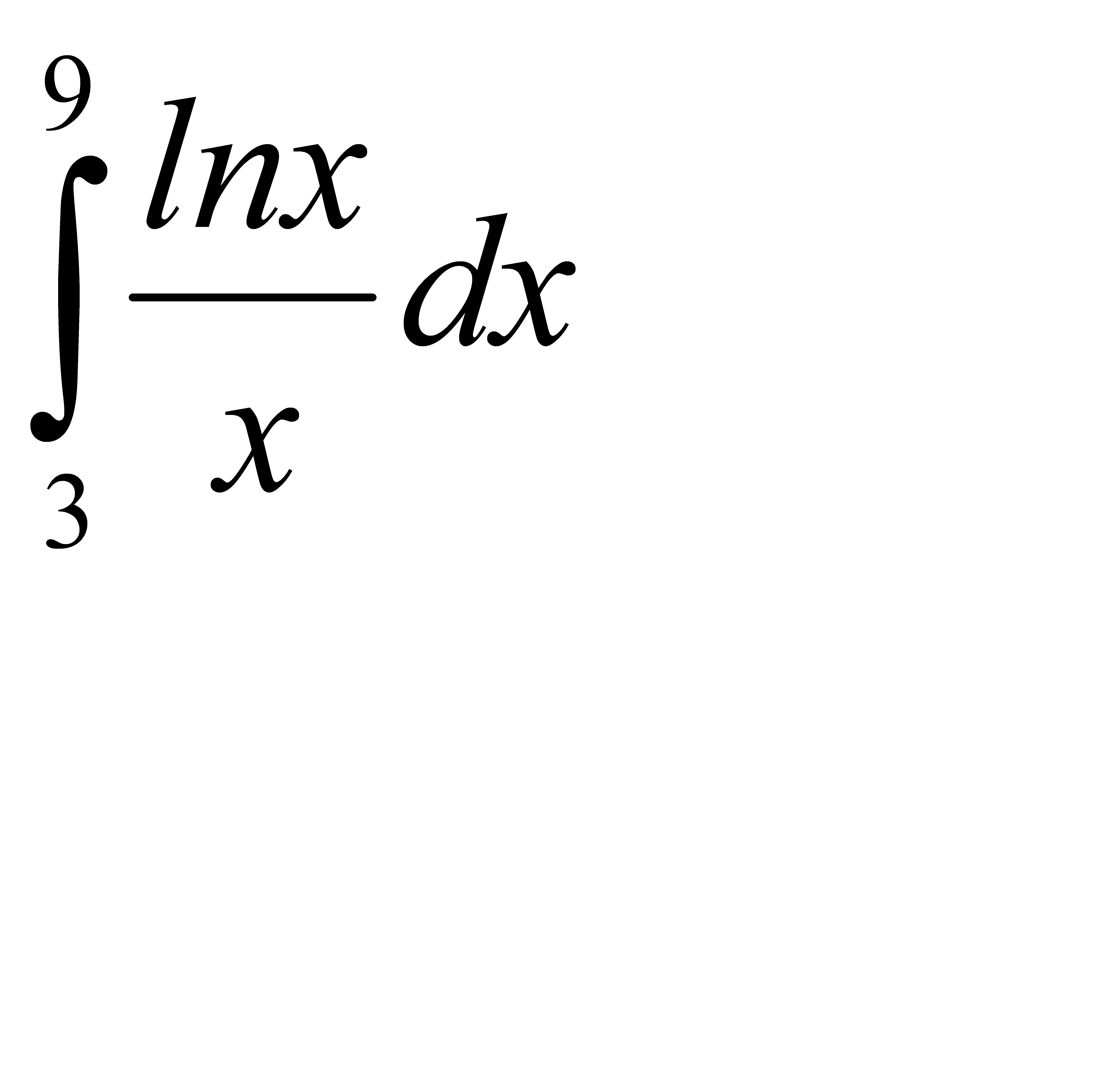 52.
52. 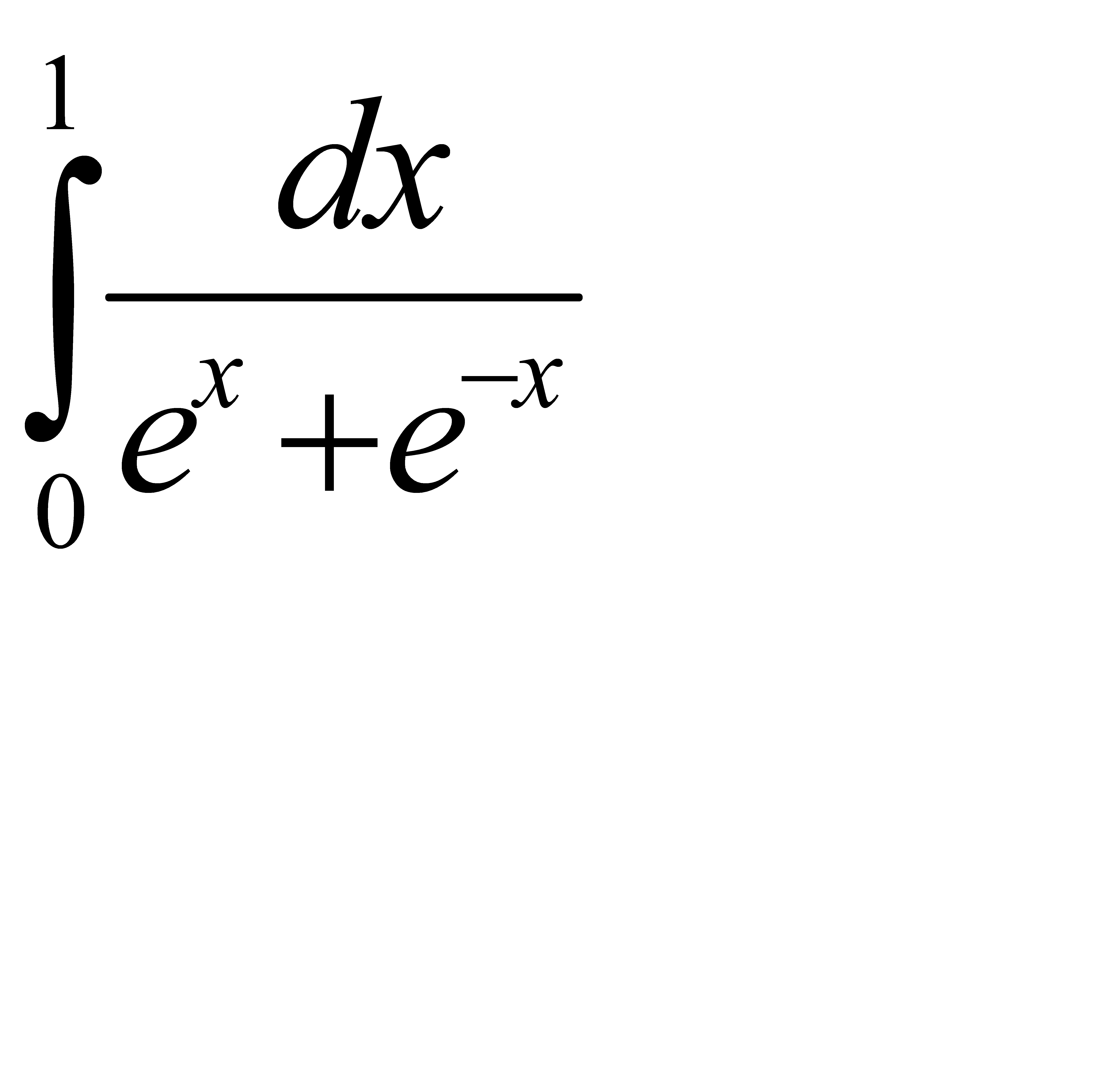 53.
53. 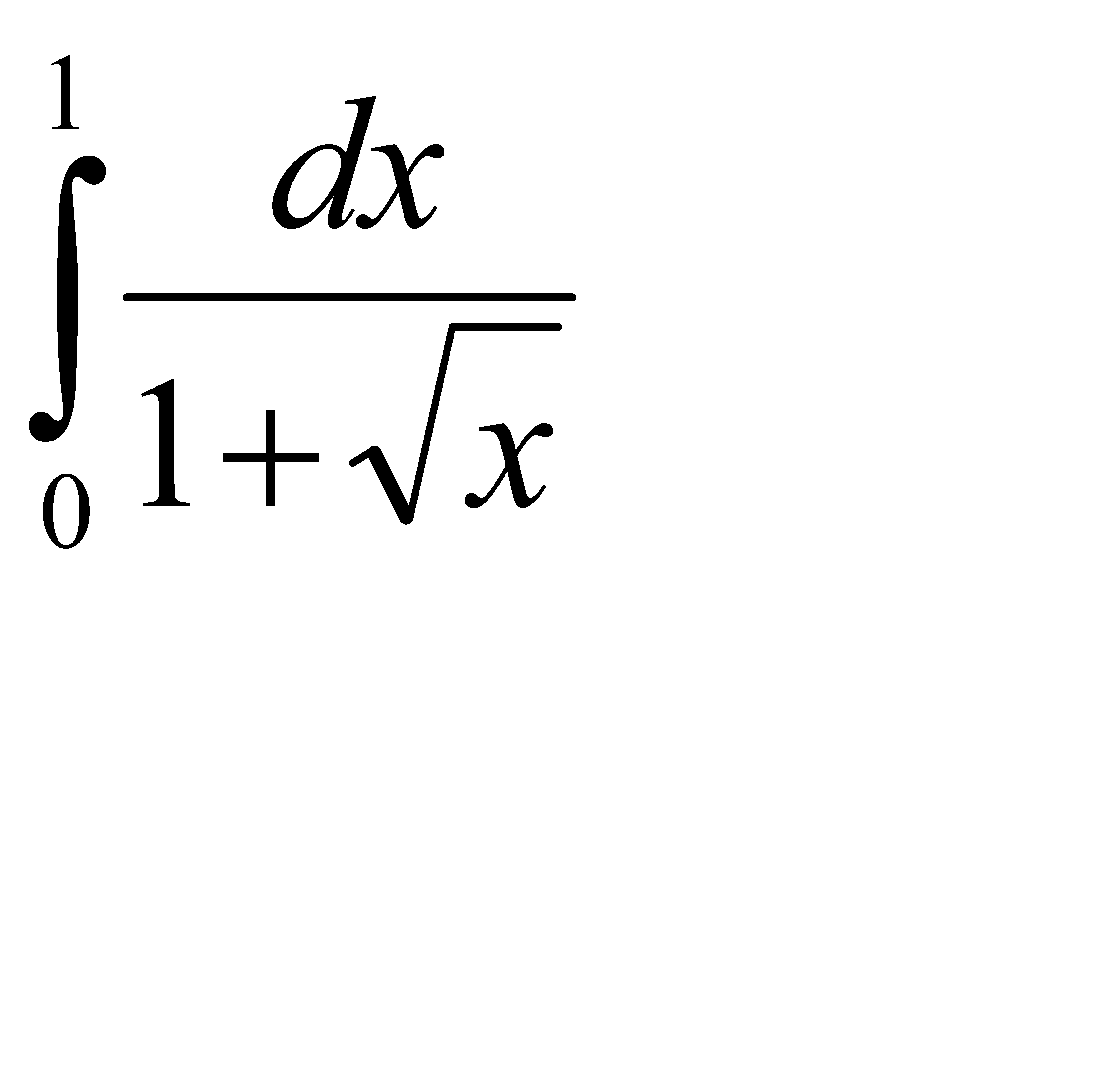
54. 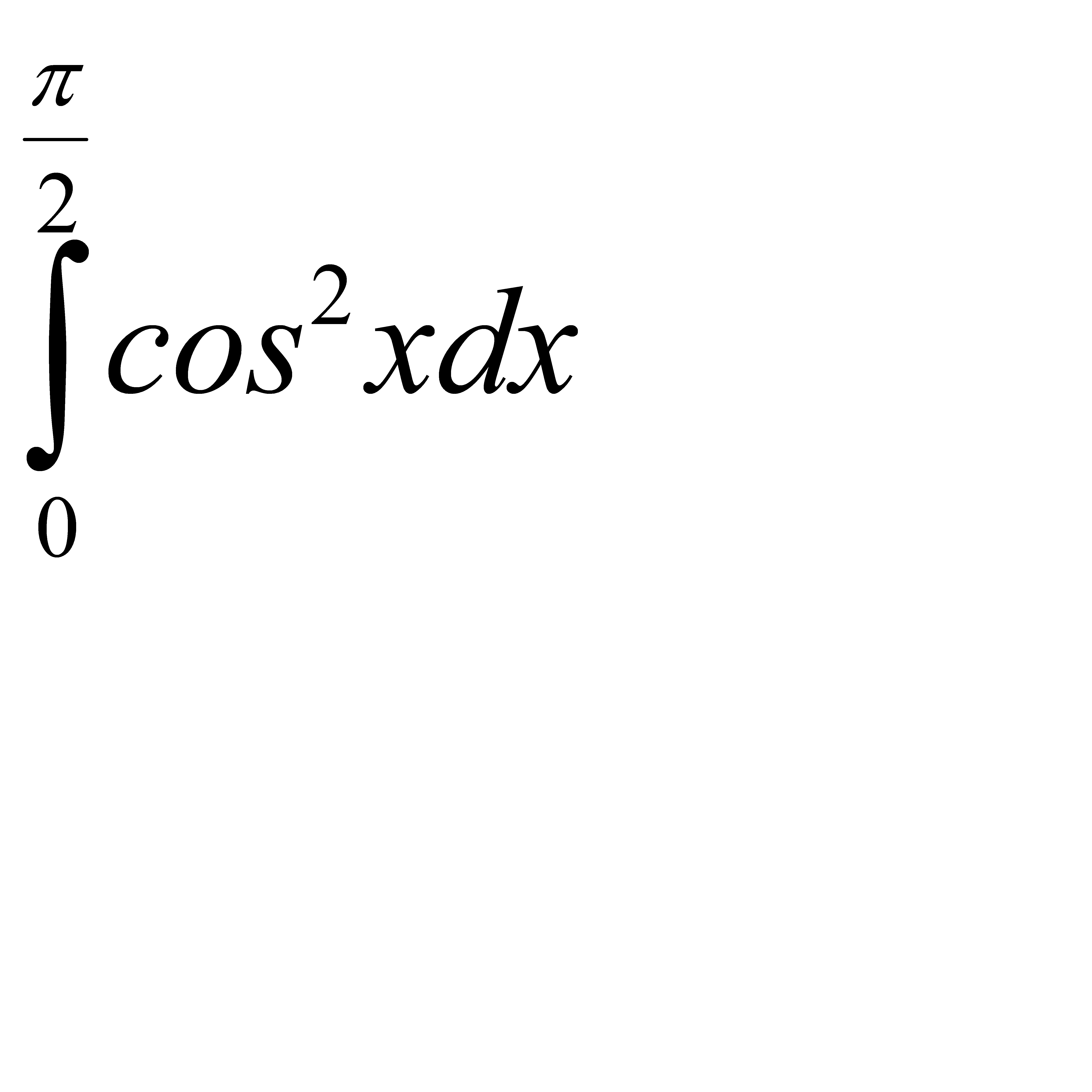 55.
55. 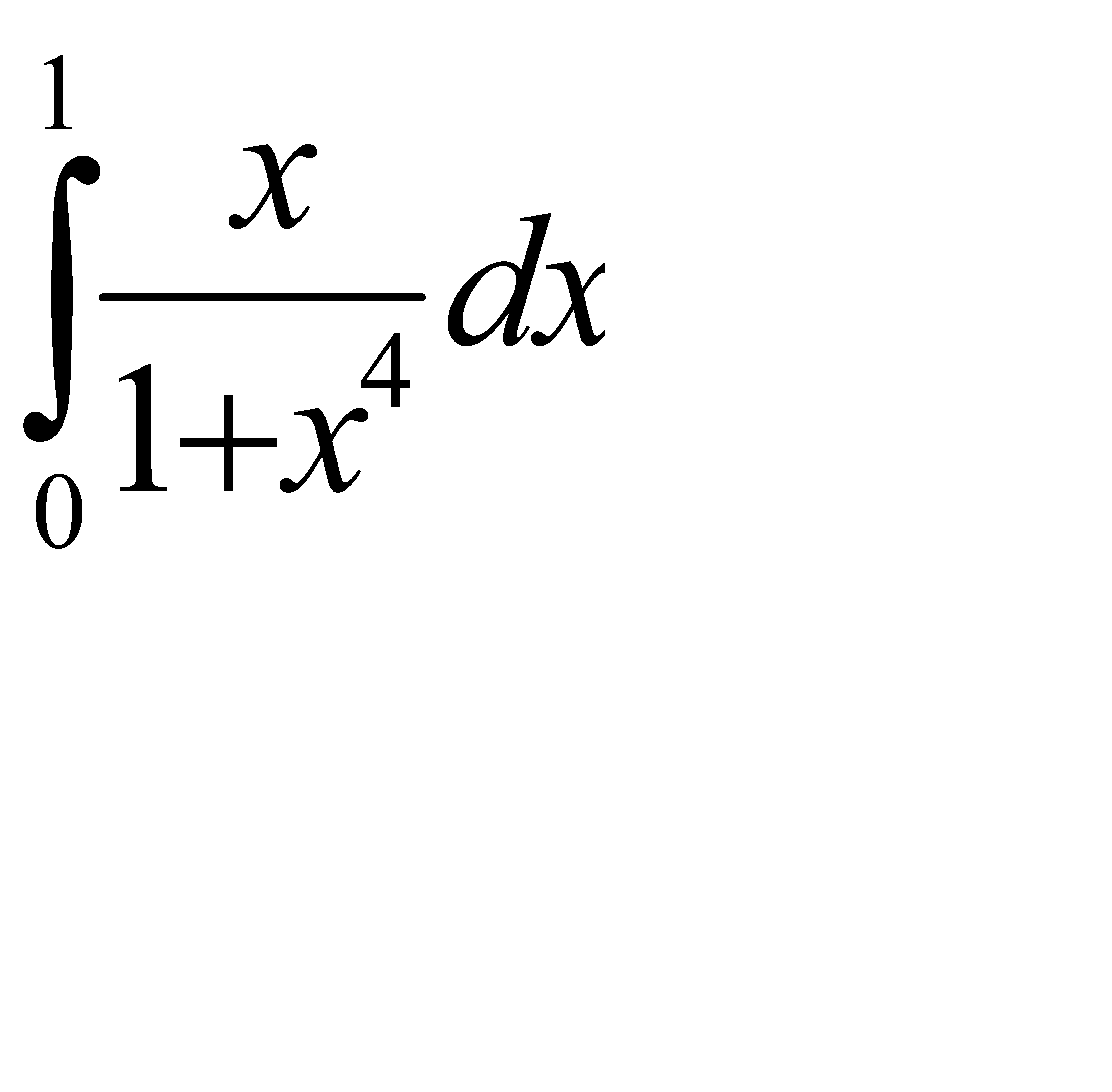 56.
56. 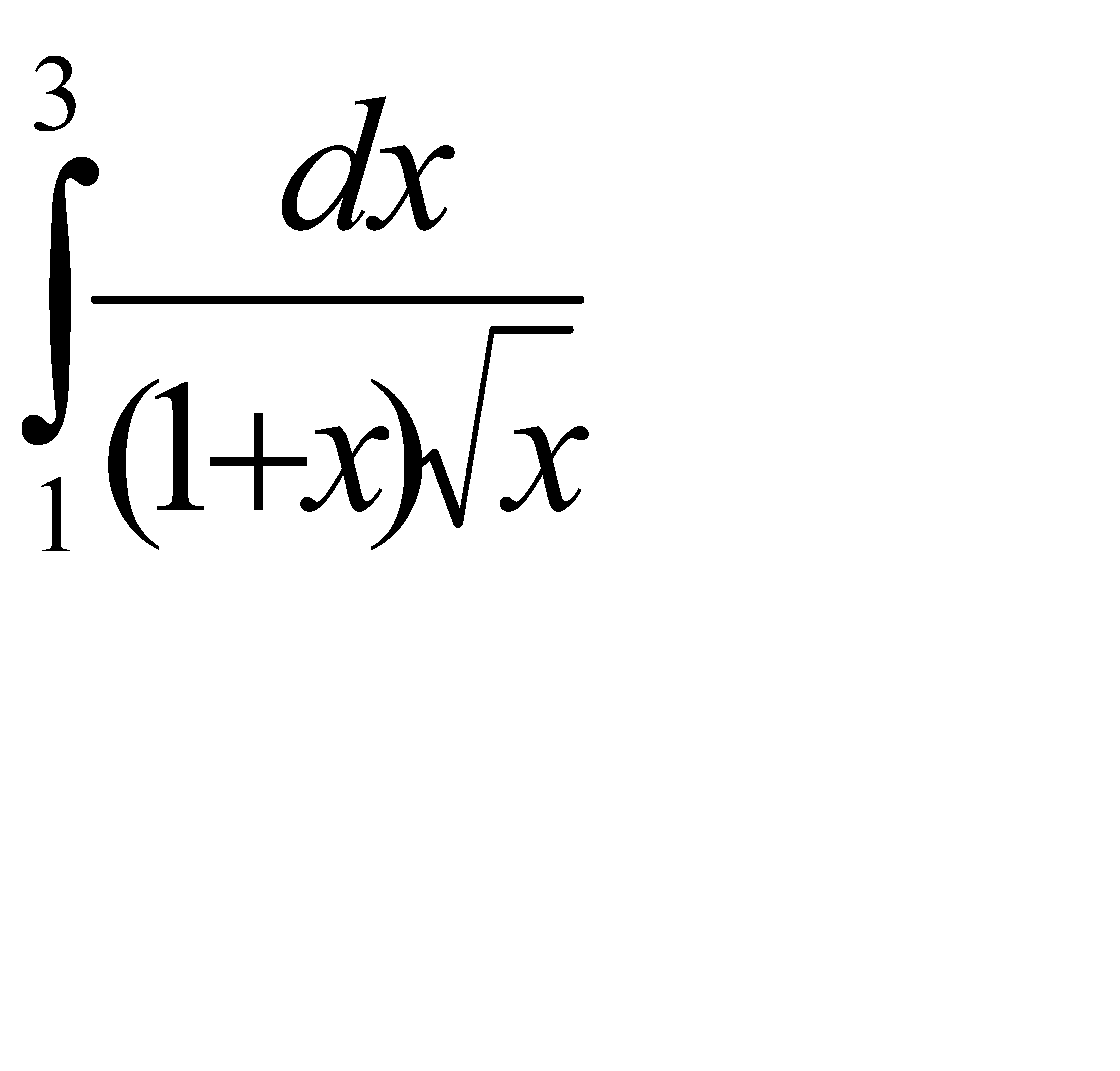
57. 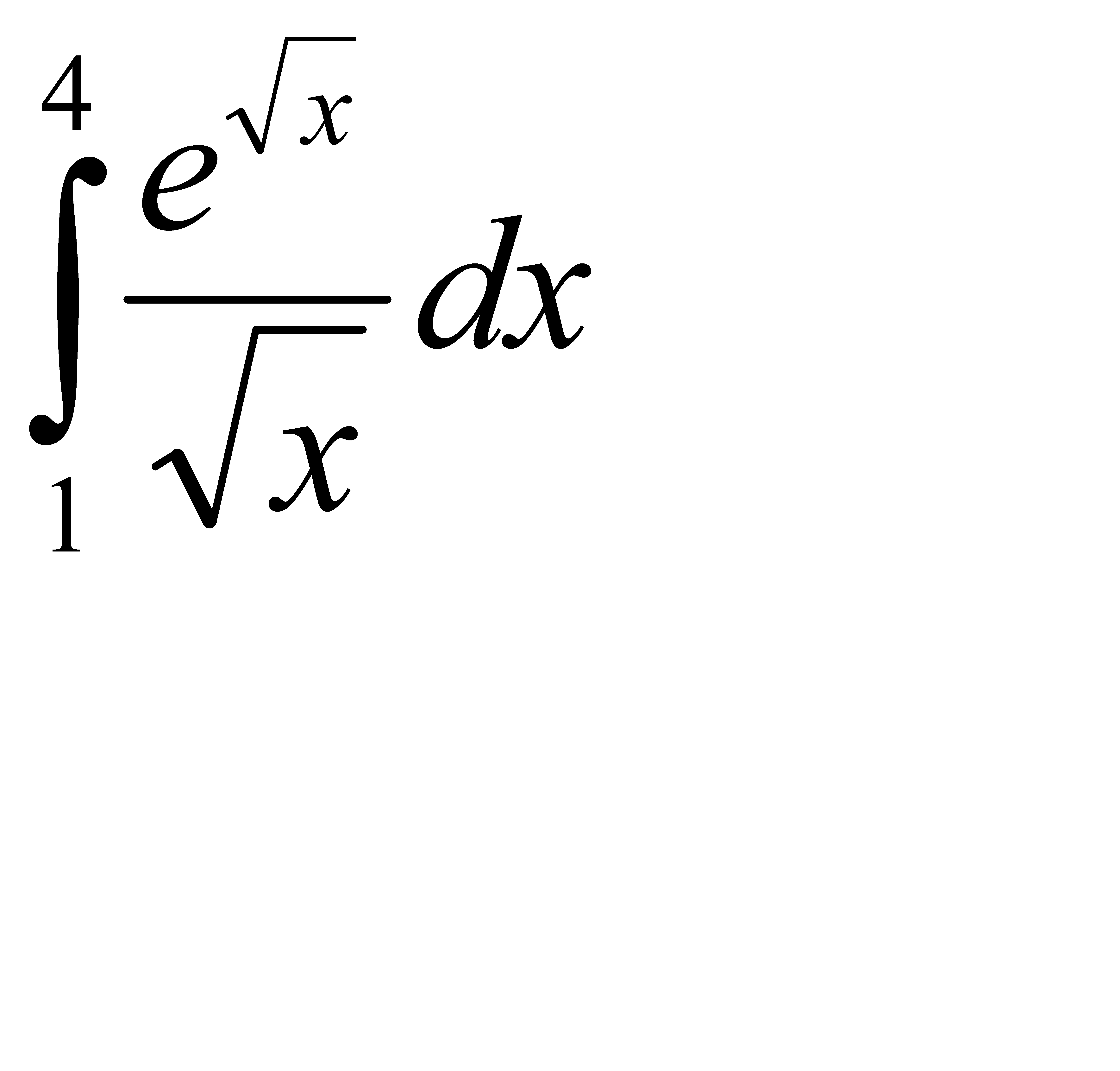 58.
58. 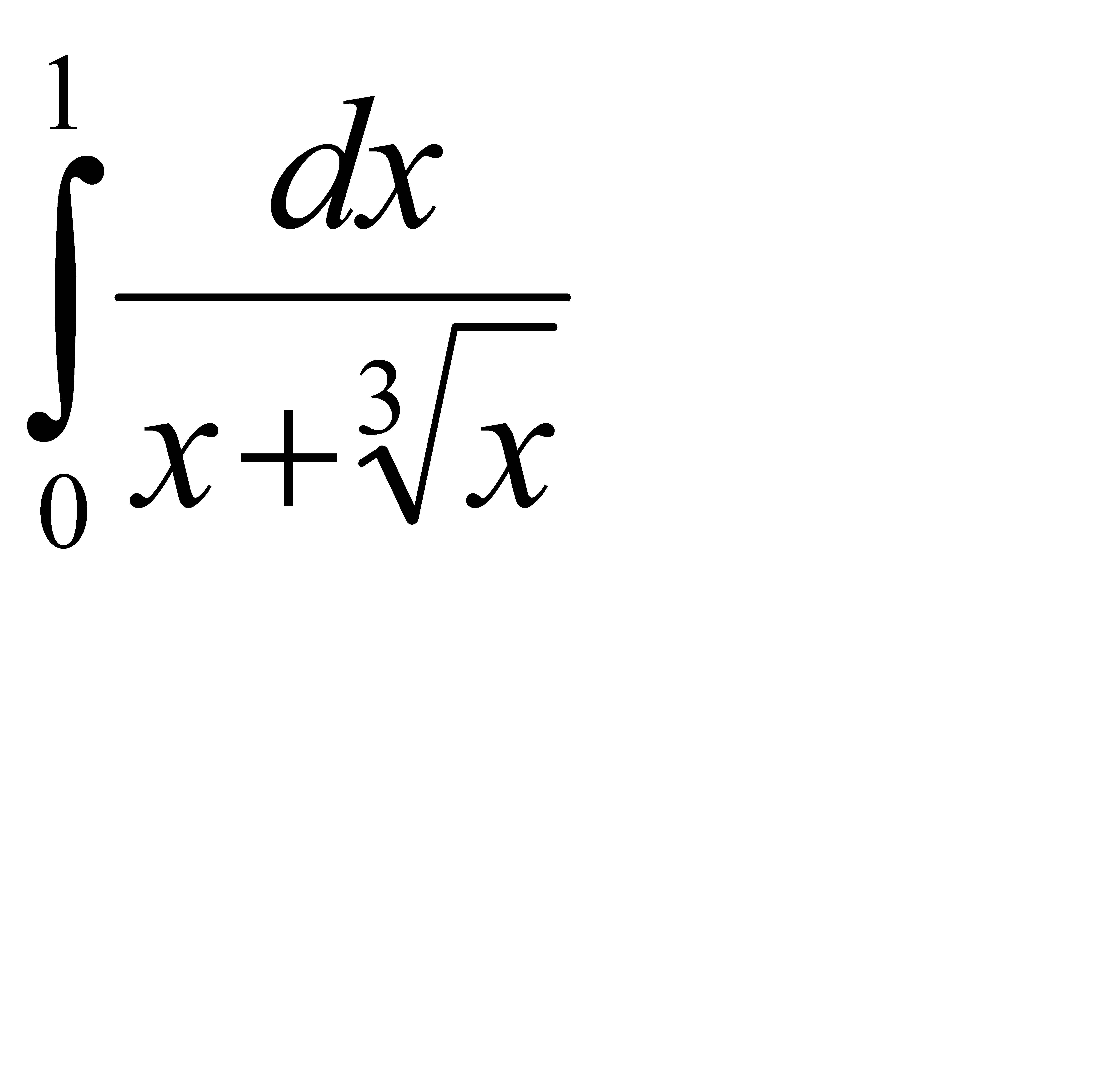 59.
59. 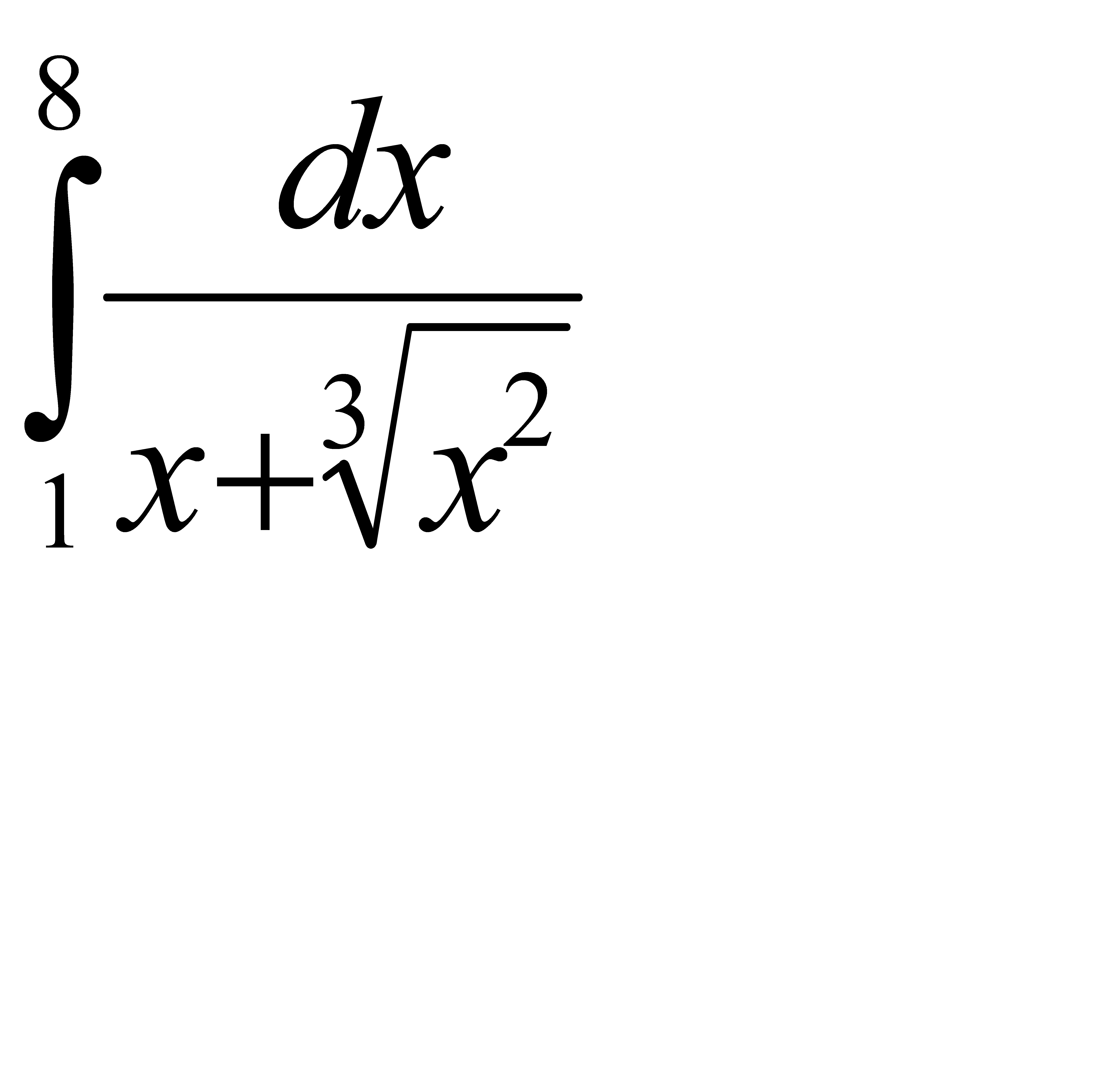
60. 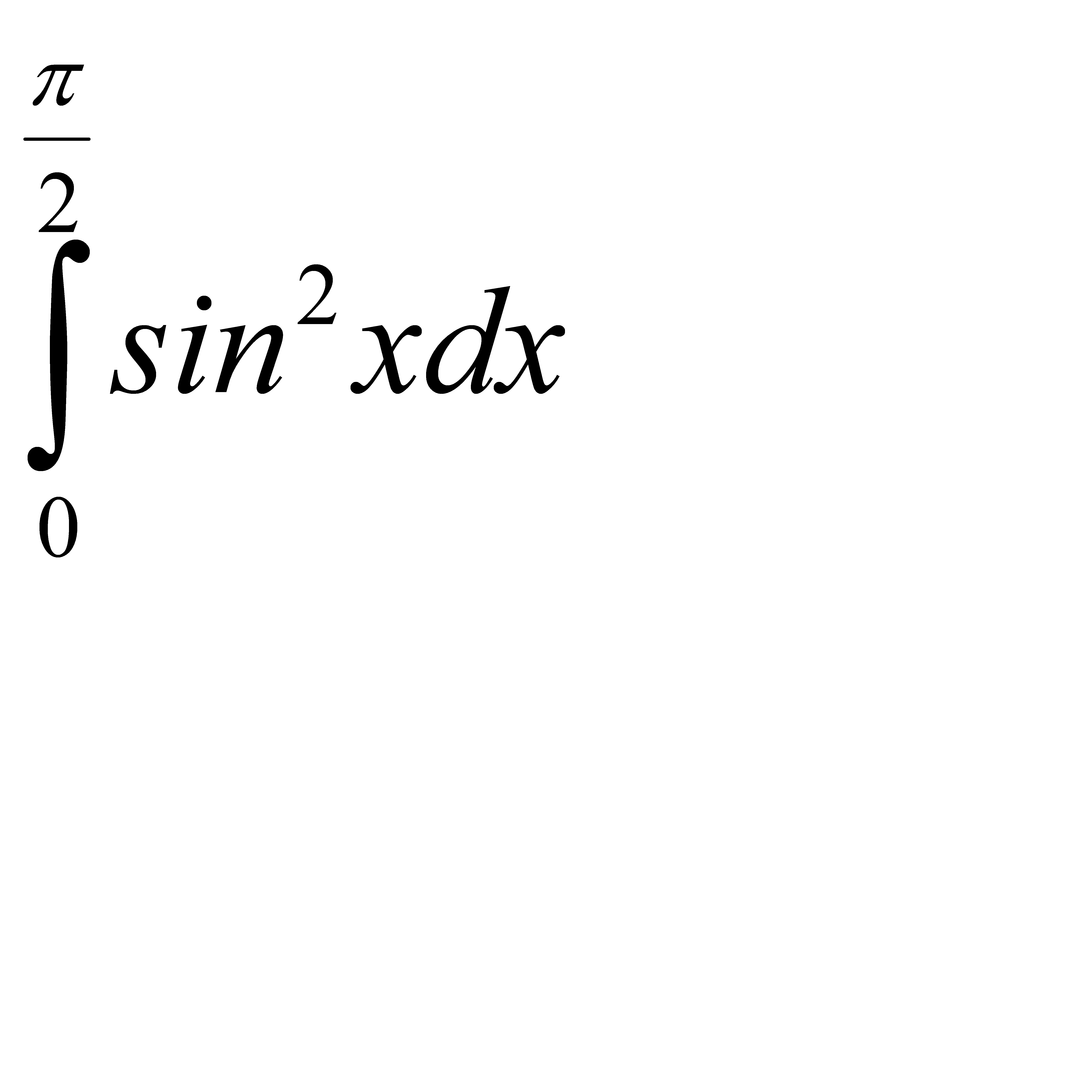
61-70. Вычислить площадь фигуры, ограниченной параболой 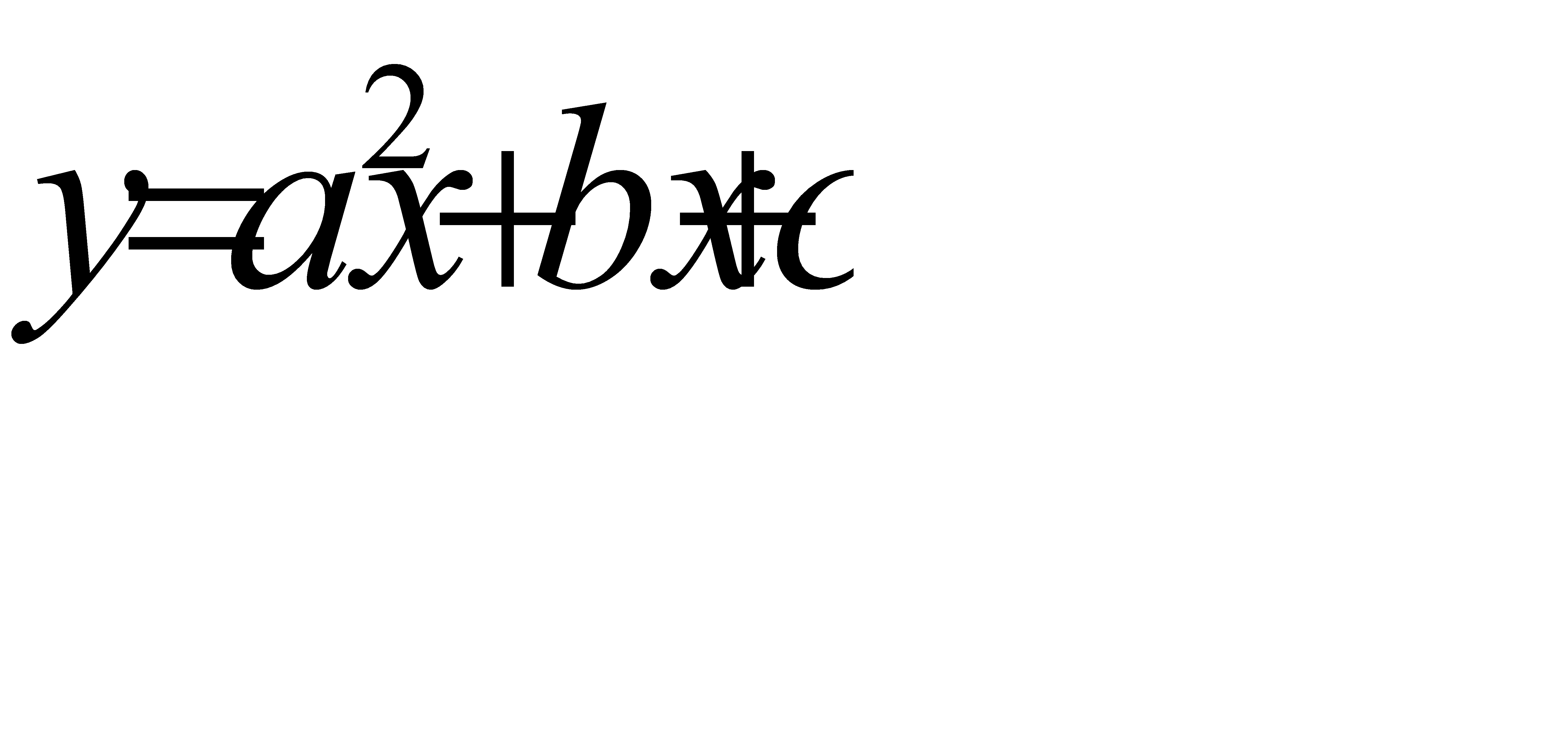 и прямой
и прямой 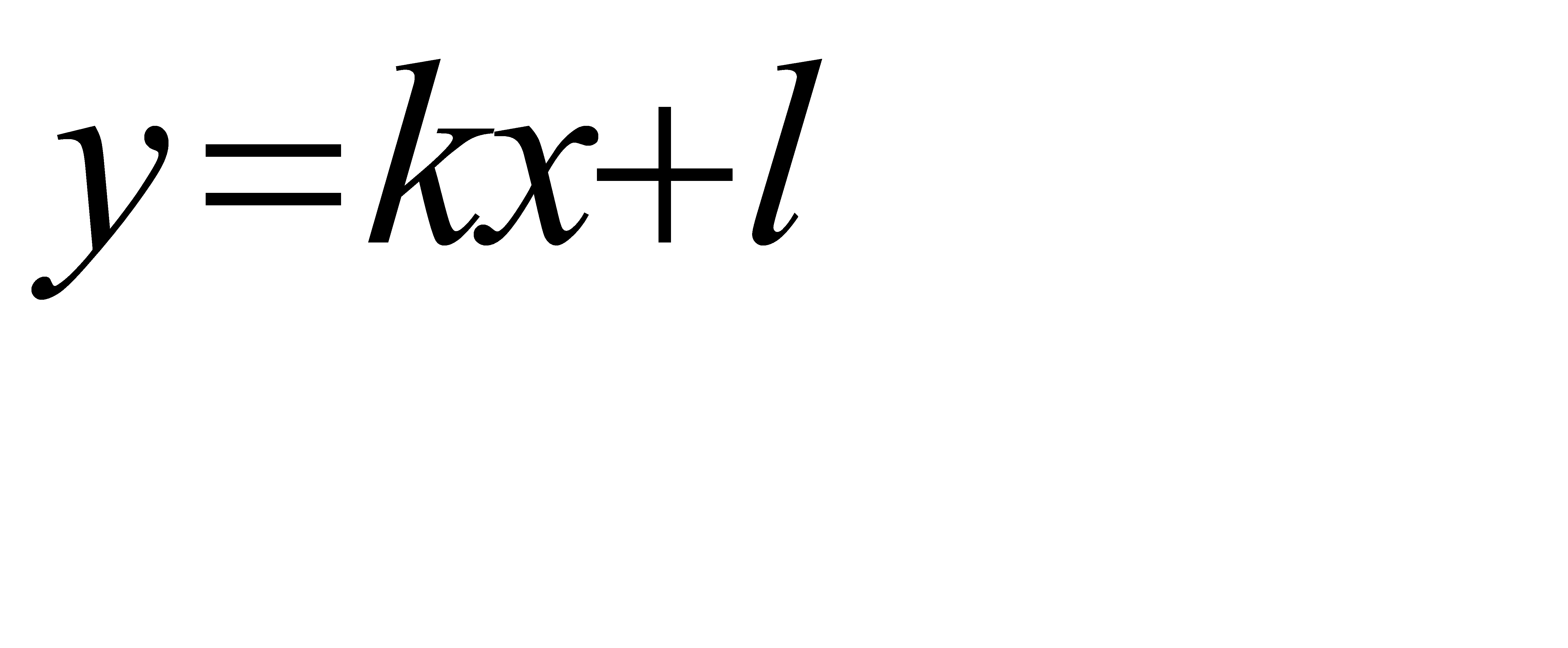 . Сделать чертеж.
. Сделать чертеж.
63. 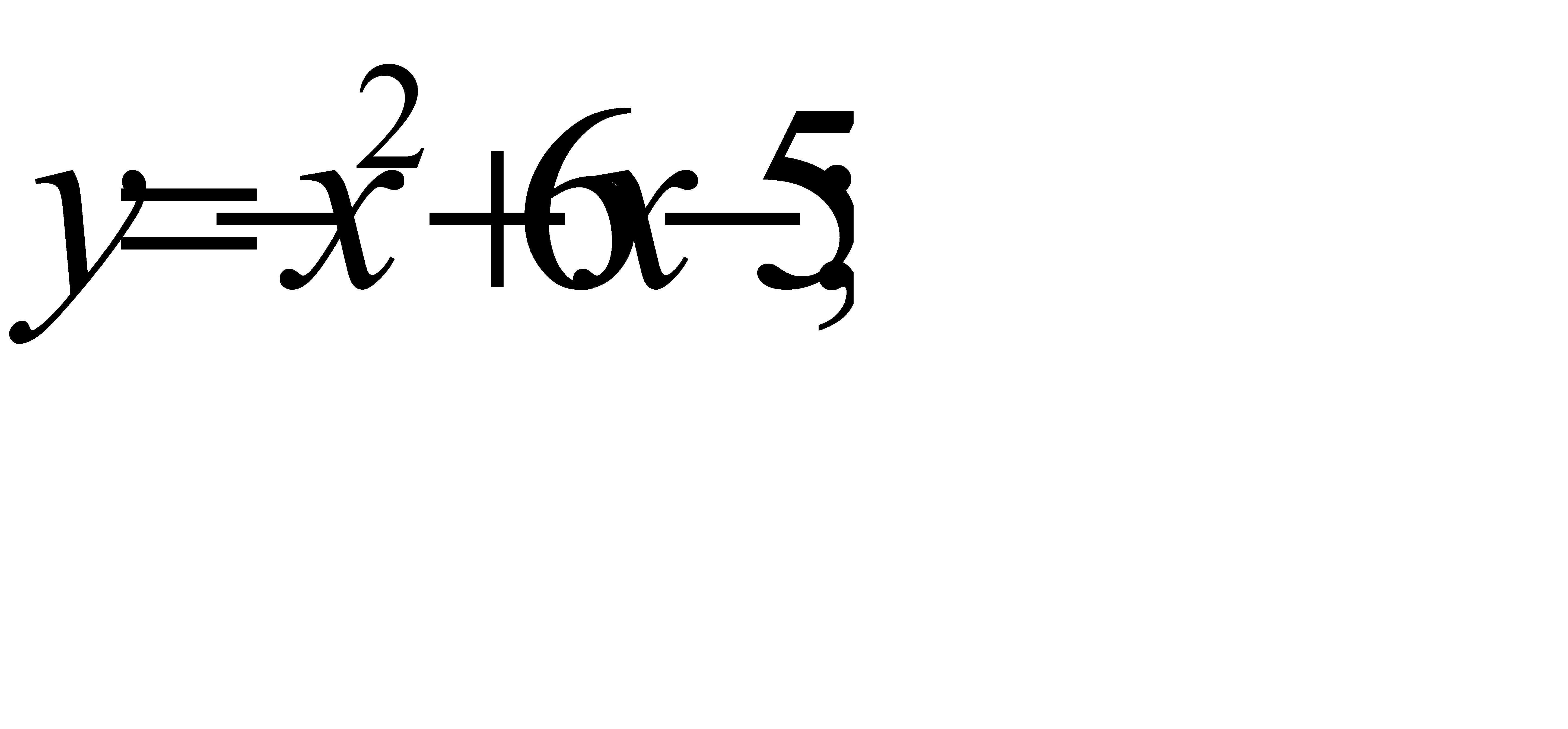
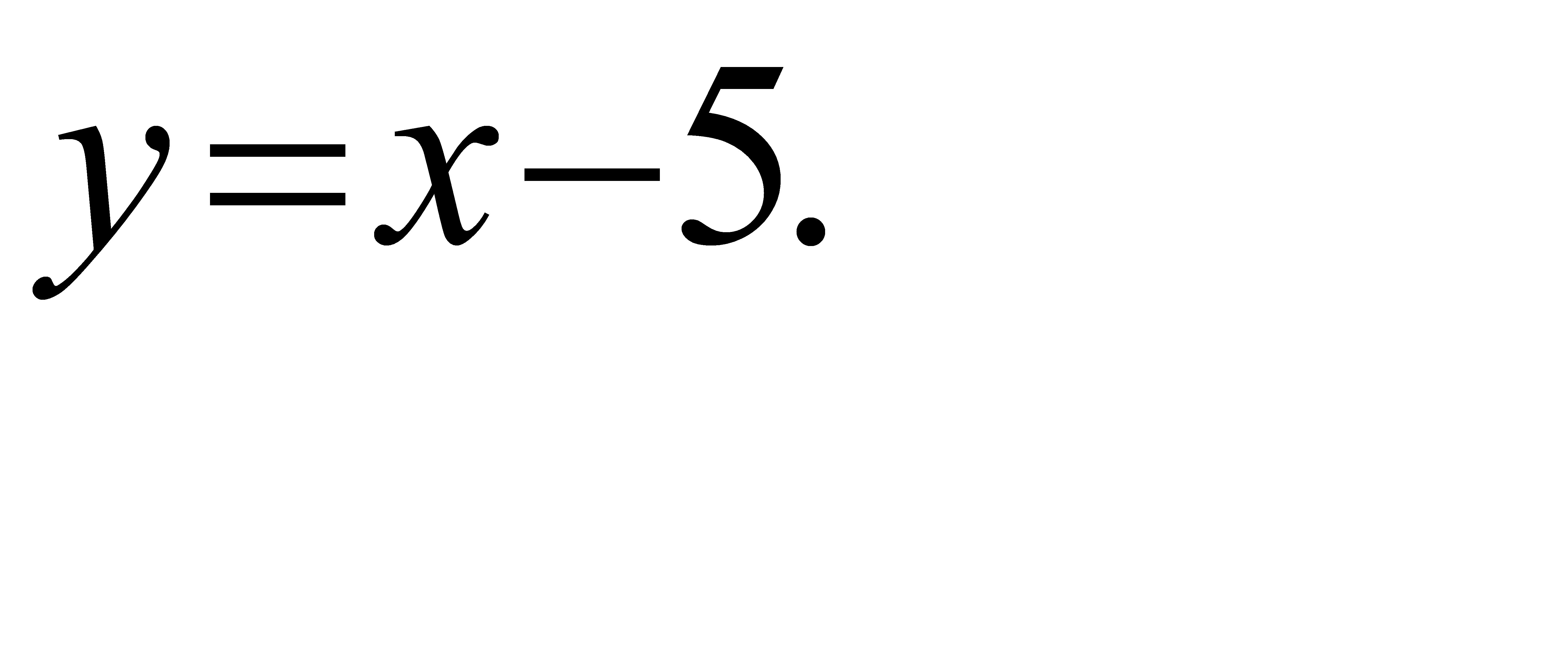
64. 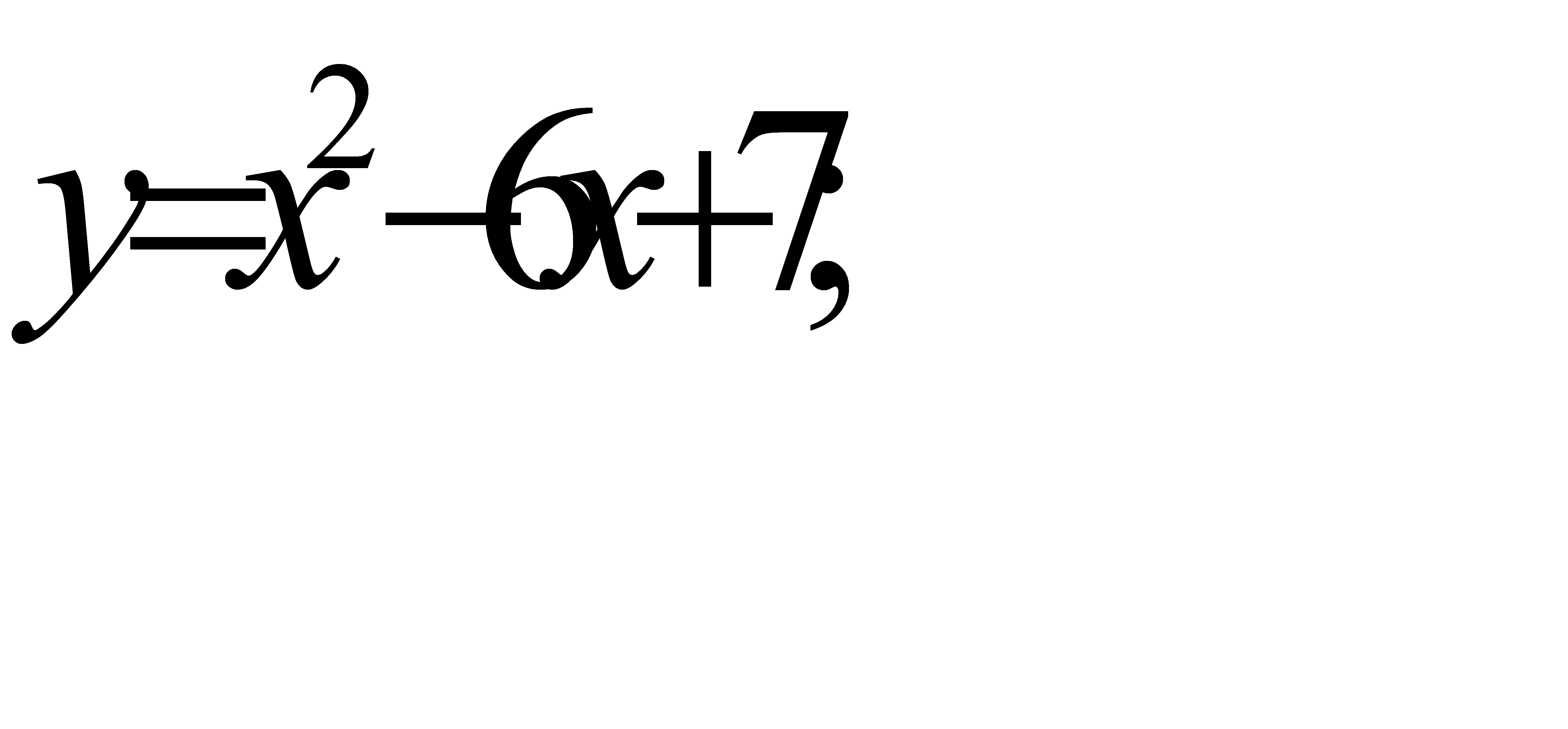
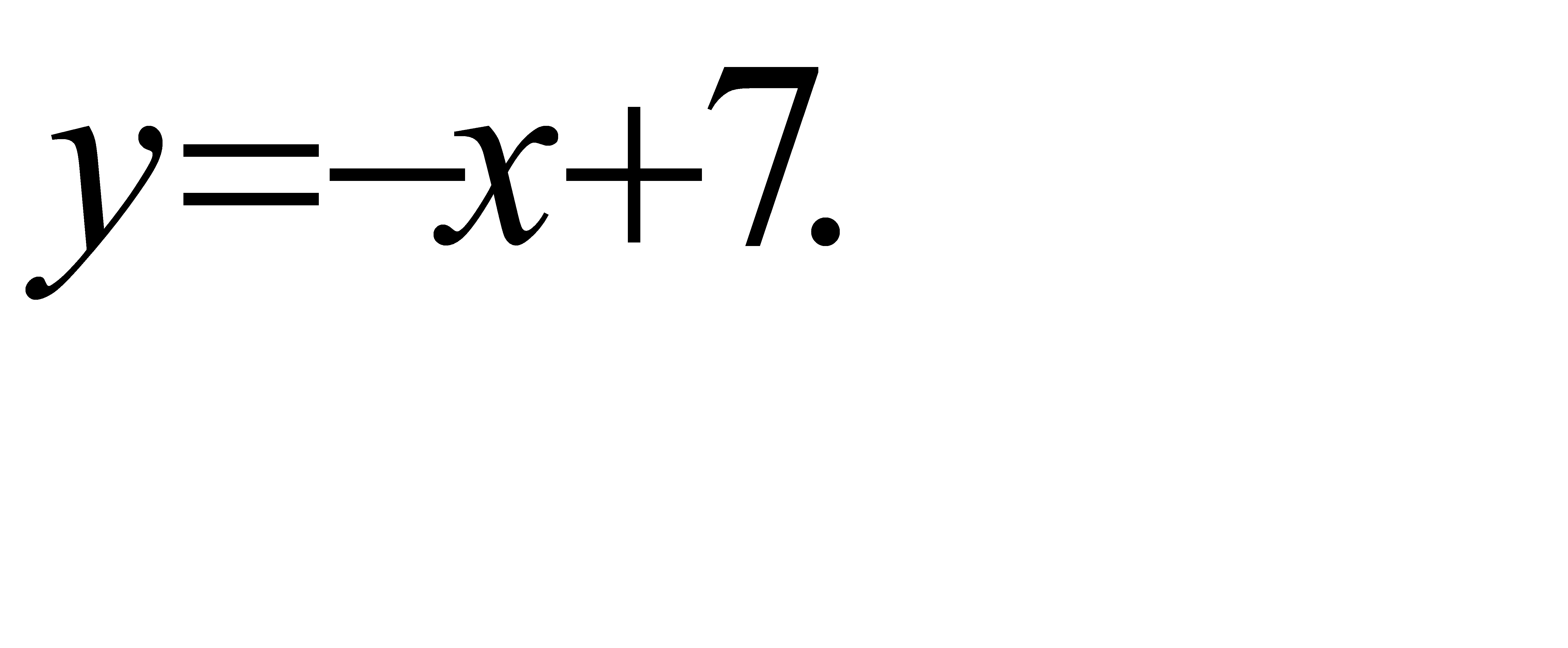
65. 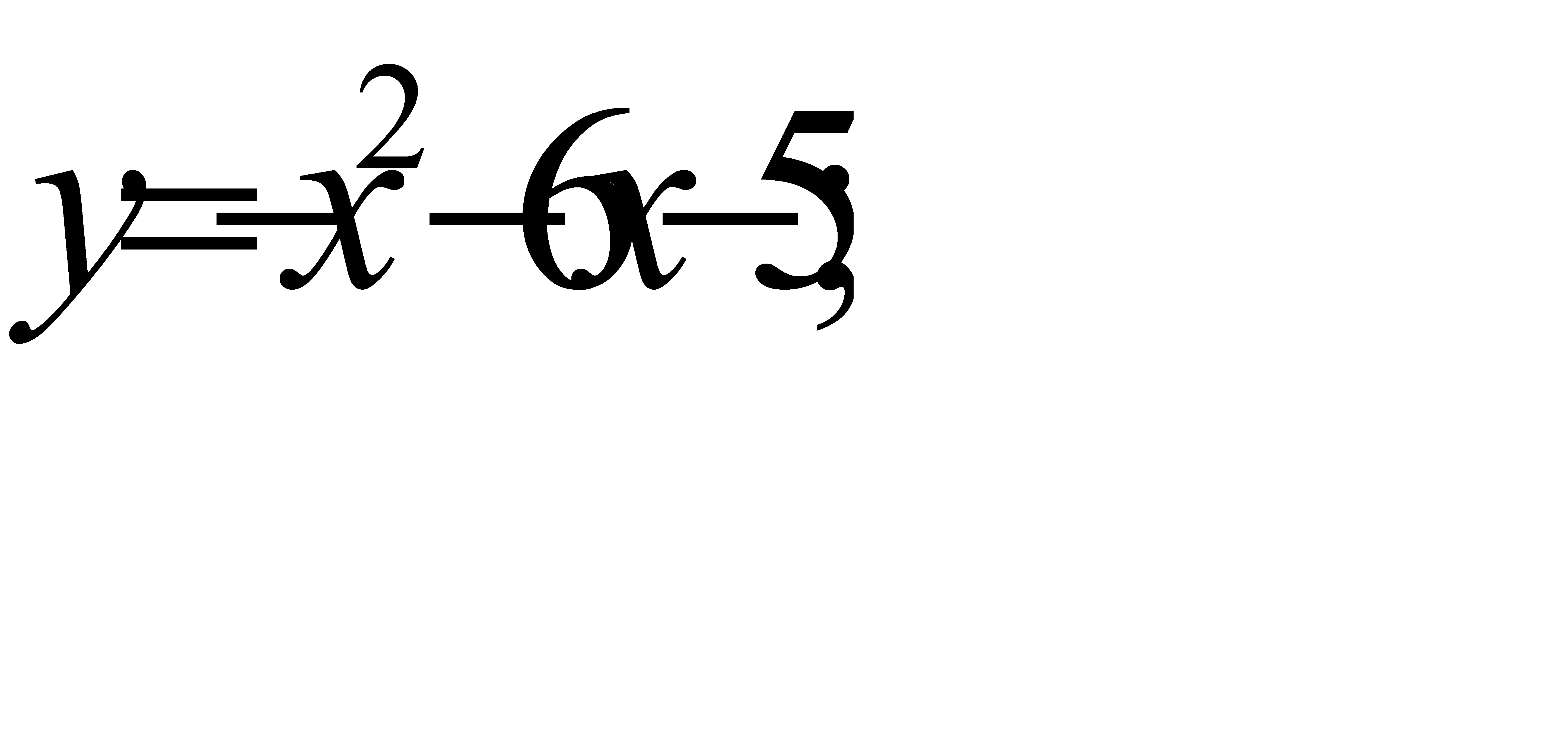
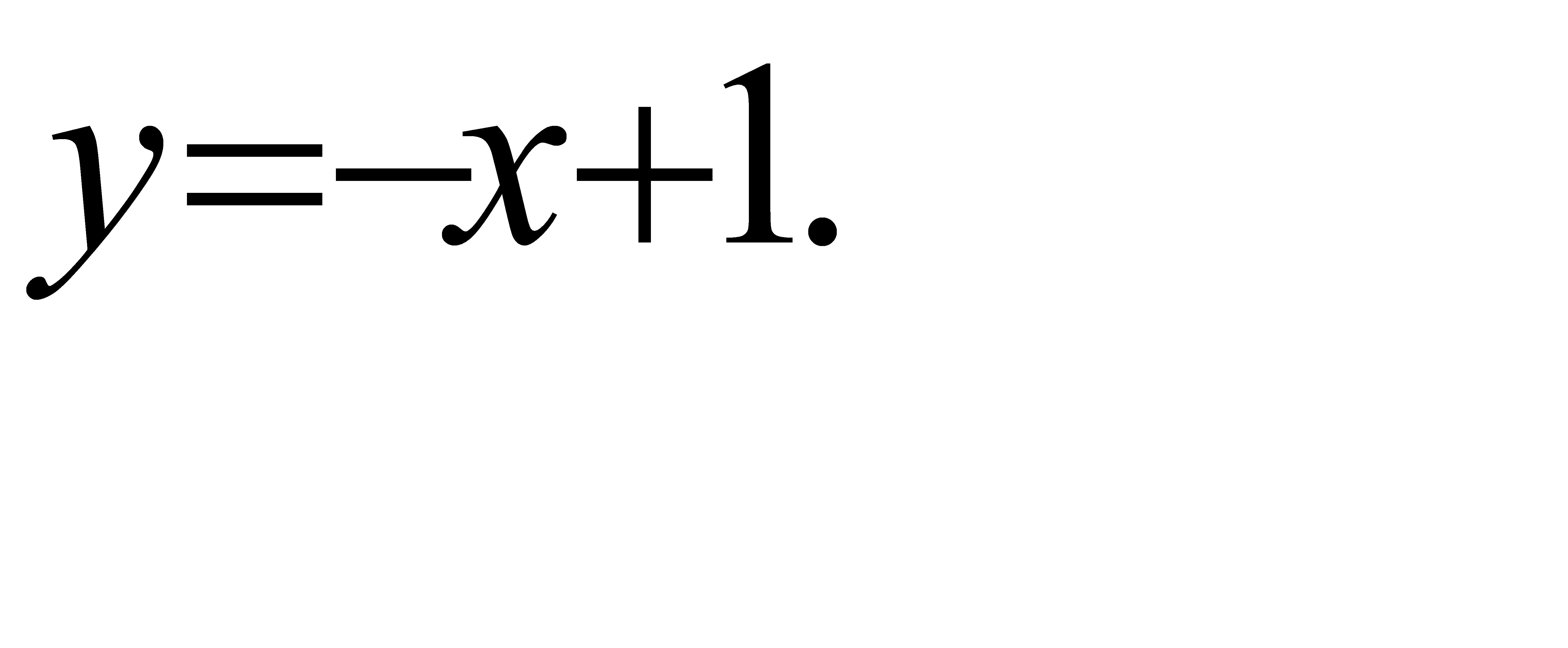
66. 
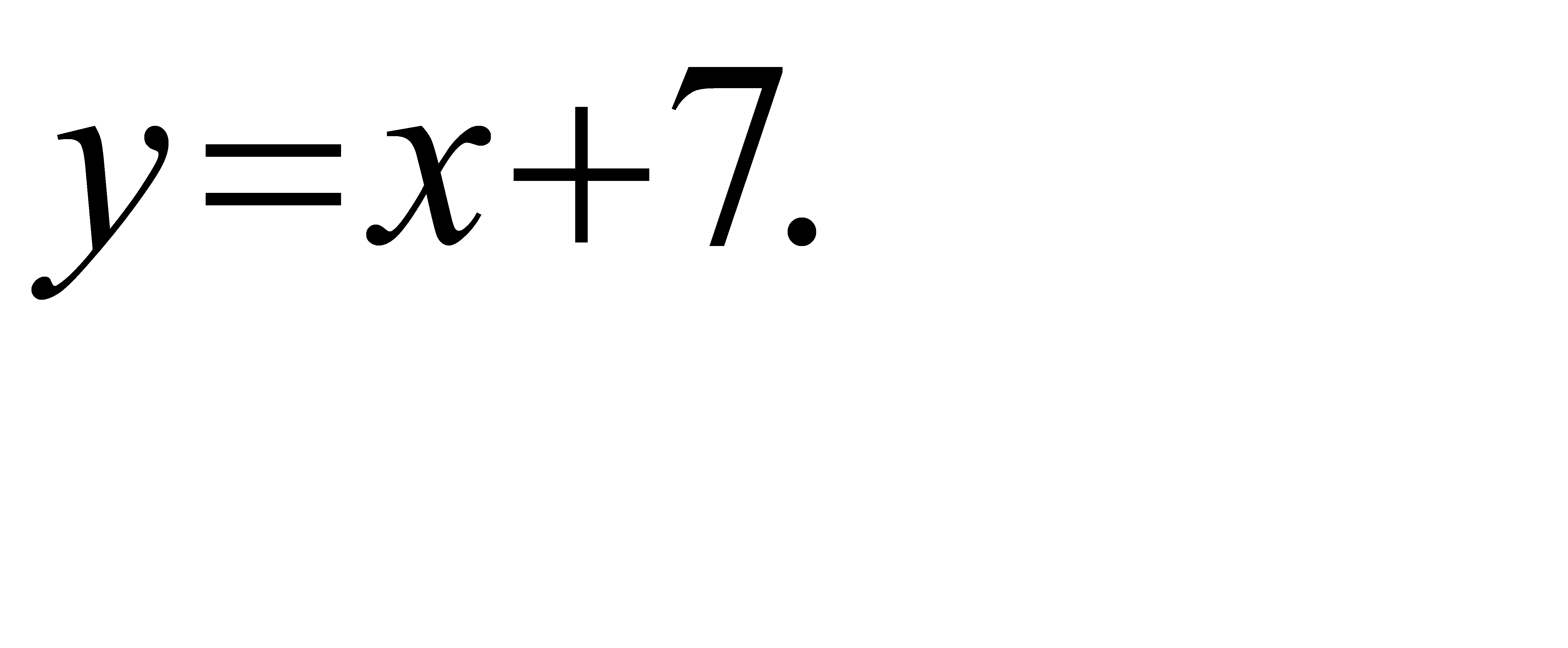
67. 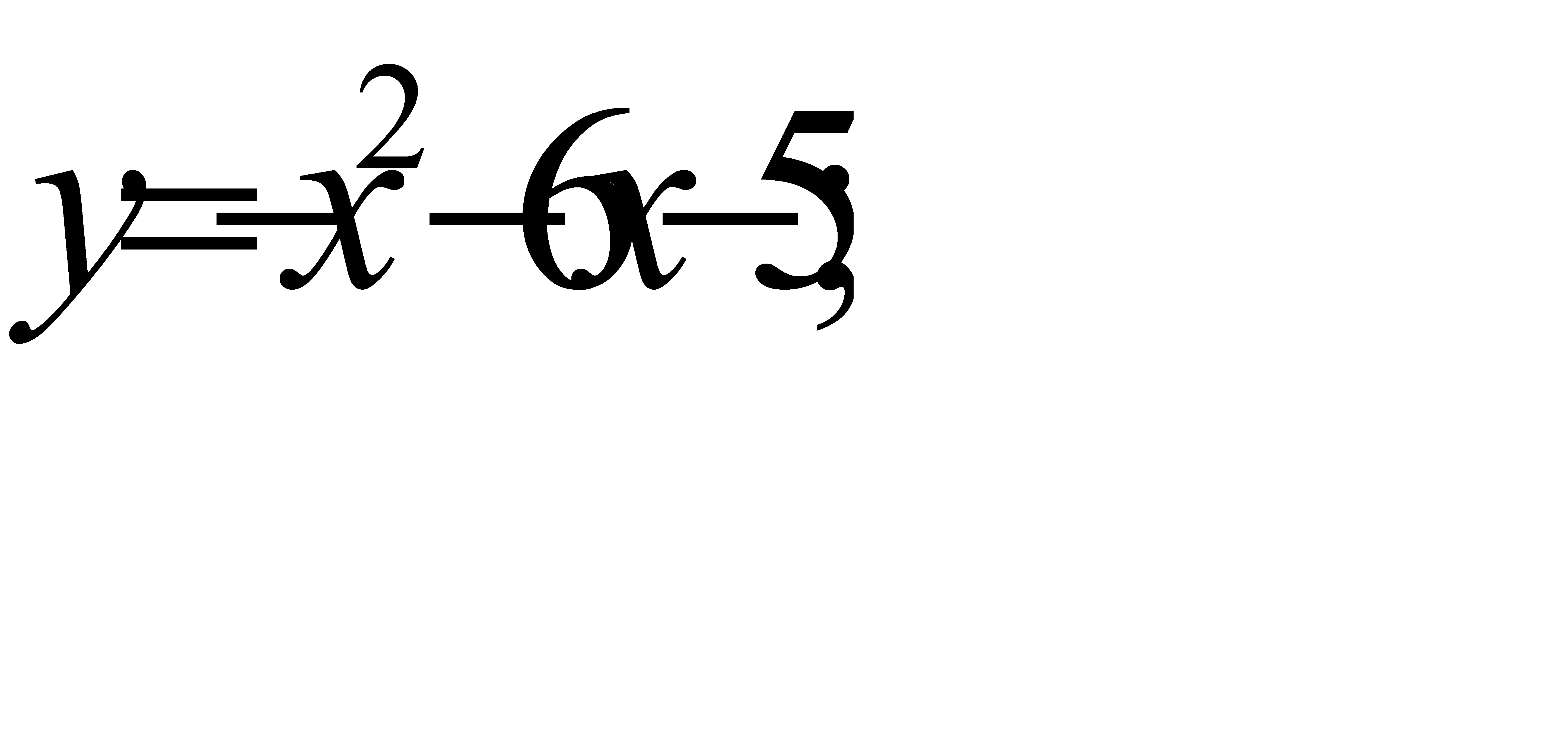
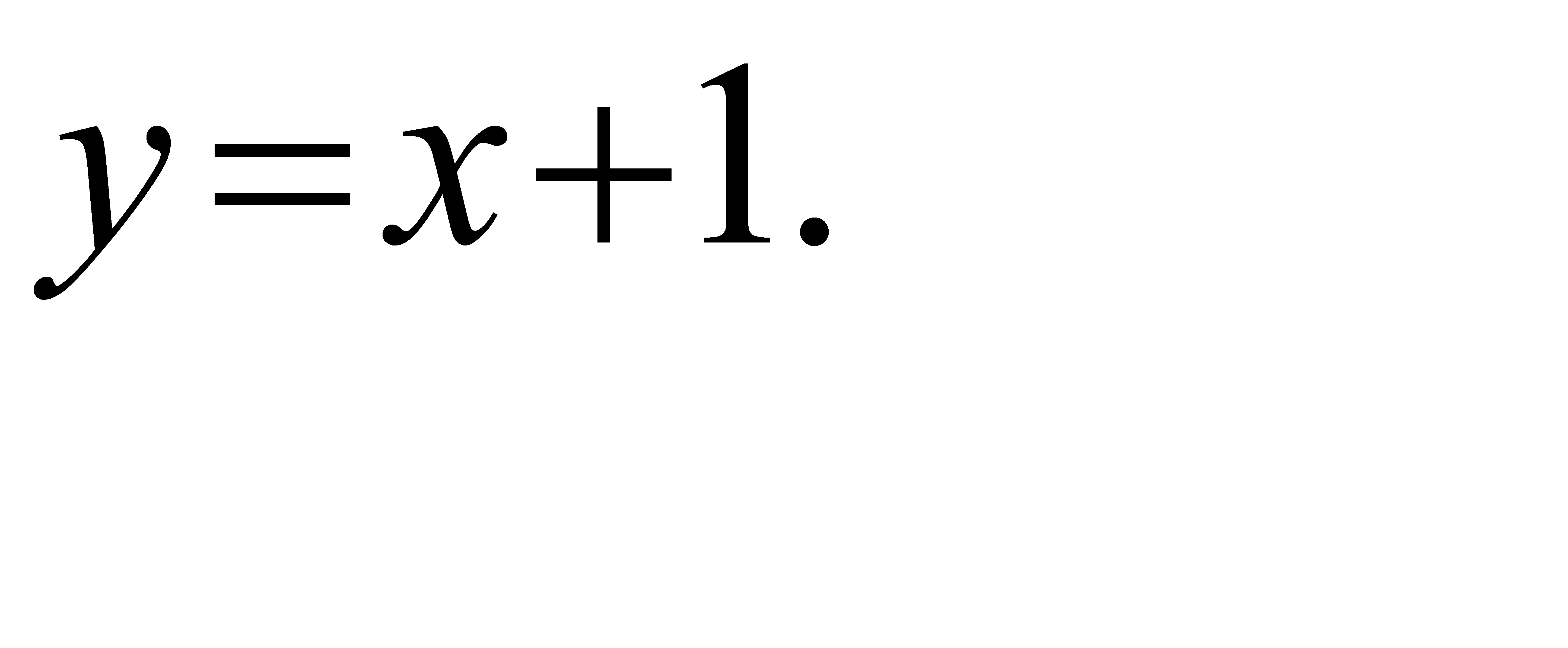
68. 
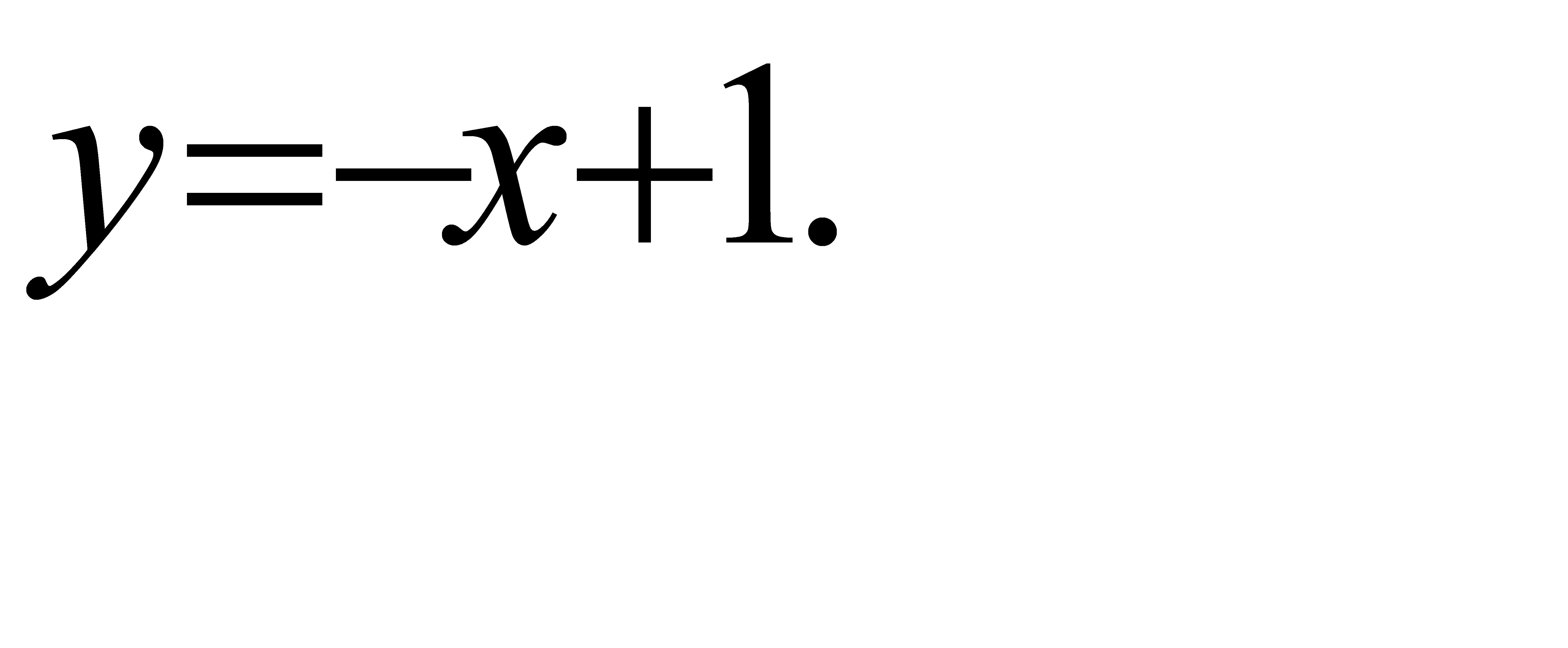
69. 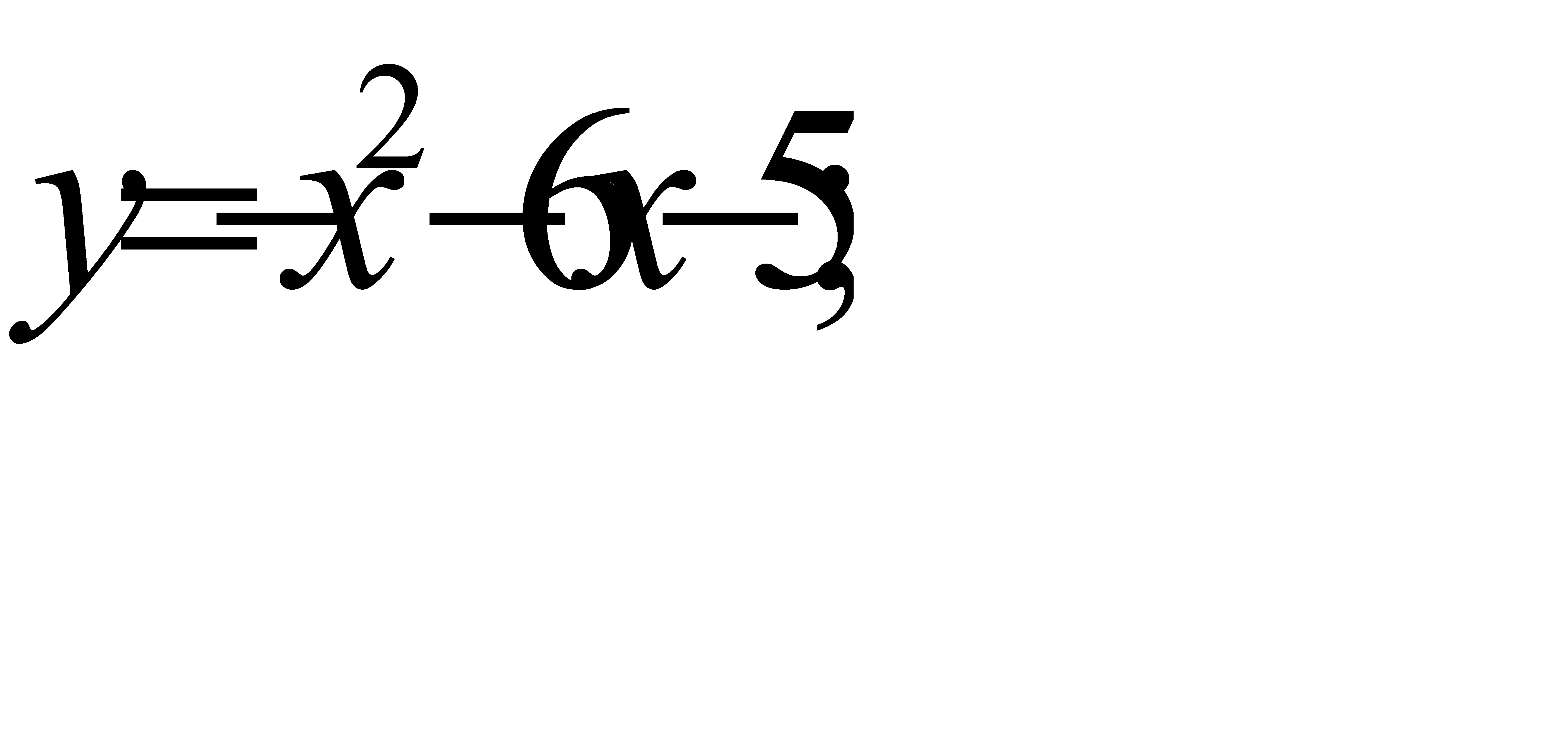
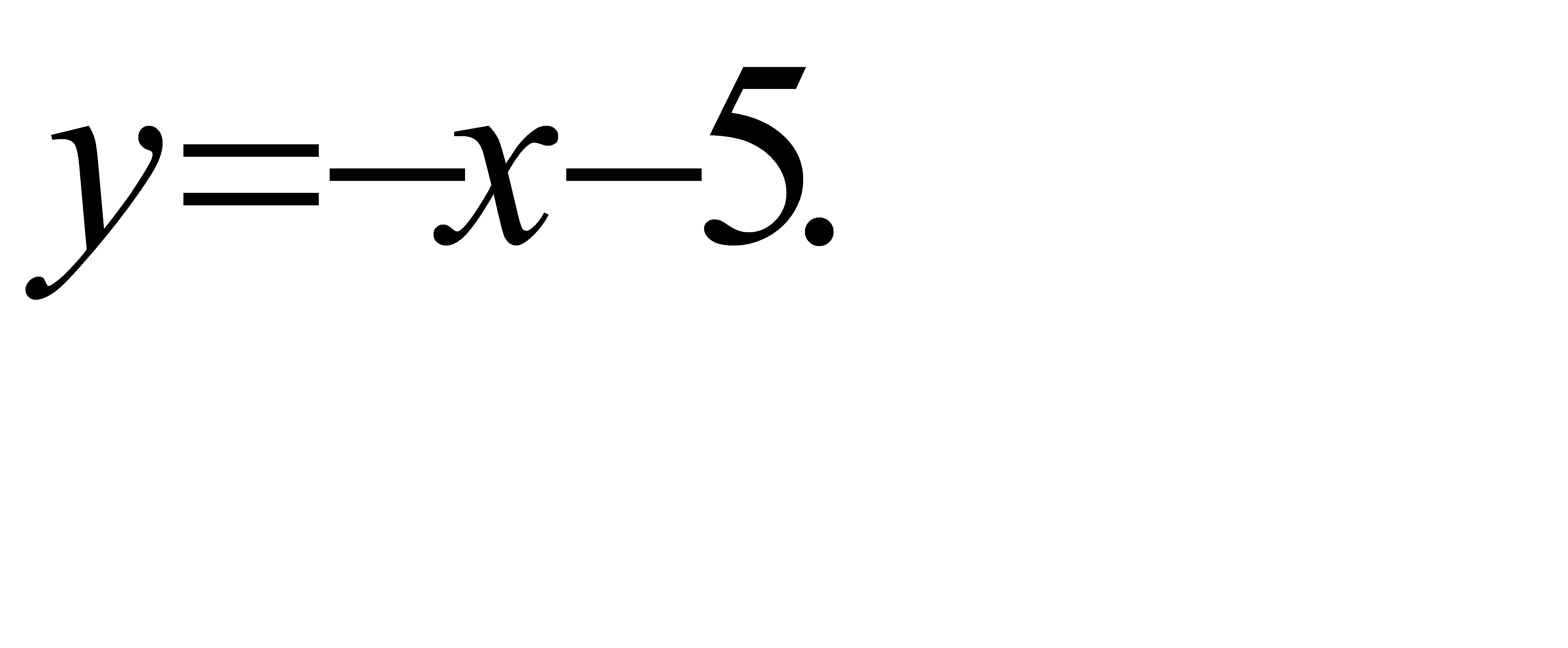
70. 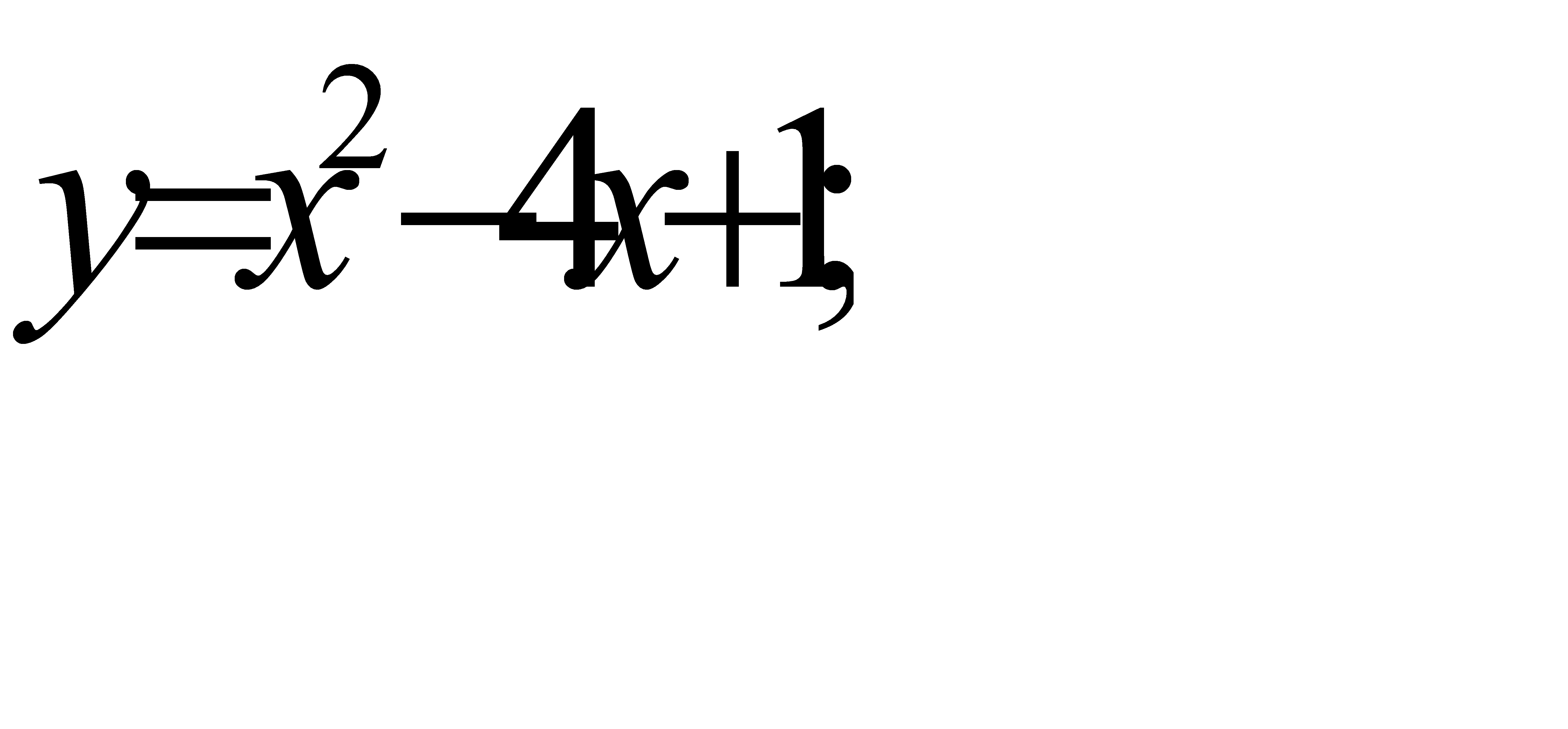
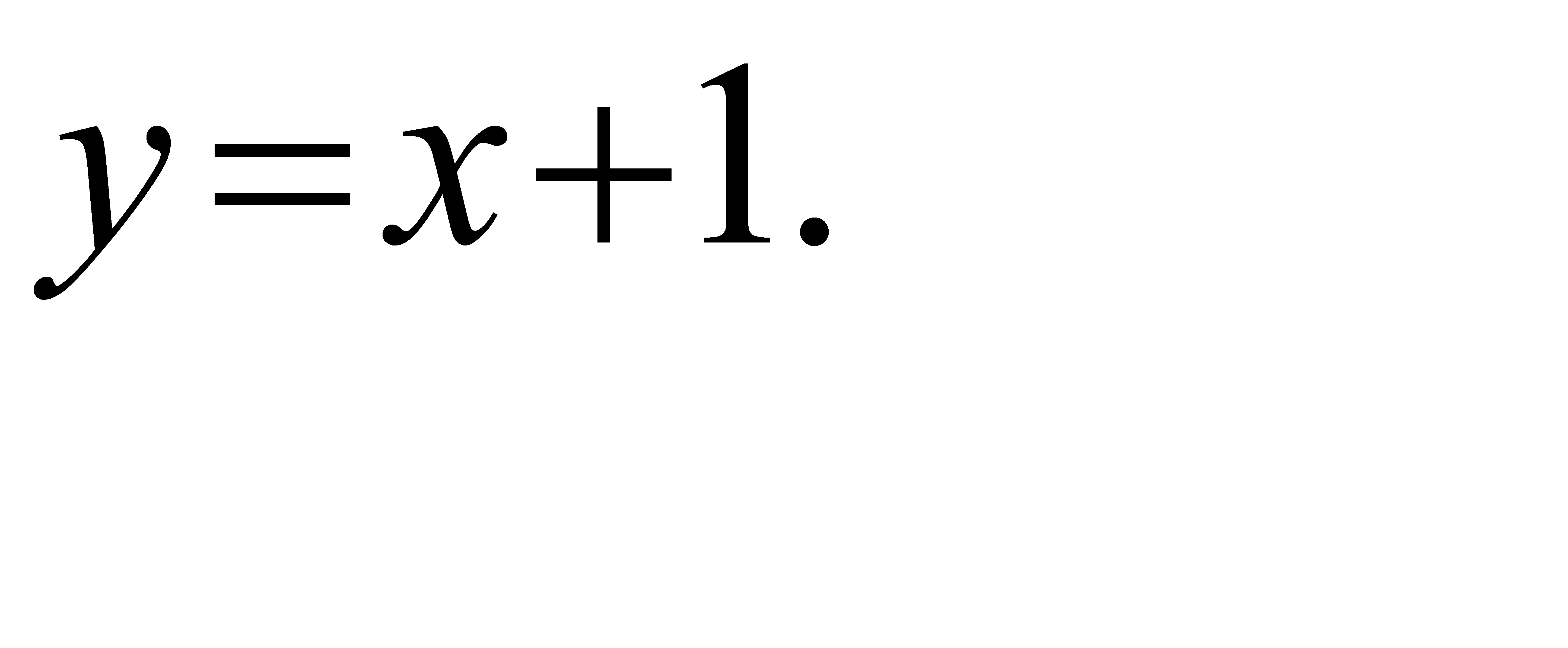
Задания для контрольной работы № 2
 2015-03-20
2015-03-20 546
546