Из основного уравнения молекулярно-кинетической теории (1) и уравнения (2) можно вывести уравнение состояния газа, а также все газовые законы, установленные экспериментально еще в XVIII веке.
Уравнением состояния газа называется уравнение, устанавливающее функциональную связь между основными термодинамическими параметрами: объемом, давлением, температурой.
Из (2) получаем, что
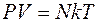 . (2a)
. (2a)
Это уравнение необходимо преобразовать так, чтобы в него вместо N входила масса газа m. Учитывая малые величины масс атомов и молекул выражать их в кг неудобно. Поэтому в молекулярной физике для характеристики масс атомов и молекул используются следующие величины:
1. Атомная единица массы (а.е.м.) - будем обозначать ее 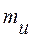 – величина, равная 1/12 массы атома 12С
– величина, равная 1/12 массы атома 12С
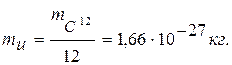 (6)
(6)
2. Безразмерная относительная молекулярная (атомная) масса 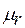 , равная отношению массы m молекулы (атома) и
, равная отношению массы m молекулы (атома) и 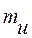 :
:
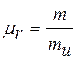 (7)
(7)
Значения 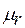 атомов приводятся в периодической системе Менделеева. Например,
атомов приводятся в периодической системе Менделеева. Например, 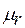 атома водорода равно 1, атома азота – 14, атома кислорода –16 и т.д. Относительная молекулярная масса молекулы равна сумме относительных атомных масс атомов ее слагающих. Например, для молекулы воды:
атома водорода равно 1, атома азота – 14, атома кислорода –16 и т.д. Относительная молекулярная масса молекулы равна сумме относительных атомных масс атомов ее слагающих. Например, для молекулы воды:
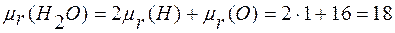 .
.
Количество граммов вещества М, численно равное относительной молекулярной массе 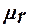 его молекул, называется молем.
его молекул, называется молем. 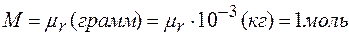
Найдем количество молекул 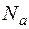 , которое будет содержаться в моле вещества. Сначала найдем массу 1молекулы из выражения (7):
, которое будет содержаться в моле вещества. Сначала найдем массу 1молекулы из выражения (7):
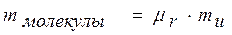 (8)
(8)
Тогда количество молекул 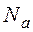 в 1 моле можно найти как:
в 1 моле можно найти как:
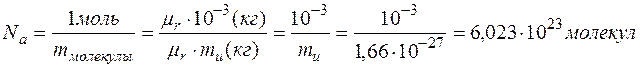 (9)
(9)
Как видим, величина 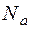 не зависит от вида вещества. В 1 моле любого вещества будет содержаться одинаковое количество молекул
не зависит от вида вещества. В 1 моле любого вещества будет содержаться одинаковое количество молекул 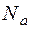 . Число
. Число 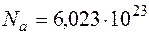 получило название числа Авогадро.
получило название числа Авогадро.
Масса 1моля вещества называется молярной массой:
М 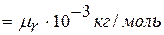 (10)
(10)
Отношение массы вещества m к молярной массе равно числу молей вещества n. Так как в моле любого вещества содержится одинаковое число молекул 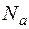 , то величина N в уравнении (2а) равна N= n
, то величина N в уравнении (2а) равна N= n 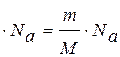 .
.
 2015-03-07
2015-03-07 956
956








