Проверка равенства дисперсий в программе EXCEL

Программа позволяет избежать трудоёмких расчётов и сразу по имеющимся выборкам определить статистическую значимость различия их дисперсий, не прибегая к табличным данным.

Диалоговое окно двухвыборочного F-теста для дисперсии кроме интервалов сравниваемых случайных величин (выборок) запрашивает значение уровня значимости α (по умолчанию берётся α = 0,05) и «метки», если первые ячейки в строке или столбце входных диапазонов содержат заголовки (рис. 7.6). Поскольку значение критерия вычисляется как отношение большей дисперсии к меньшей по формуле (7.3), в «интервал переменной 1» (см. рис. 7.6), необходимо вносить выборку с большей, а в «интервал переменной 2» - выборку с меньшей дисперсией. Это является обязательным условием правильного расчёта.

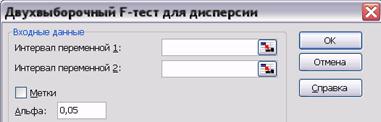
Рис. 7.6. Диалоговое окно инструмента анализа «Двухвыборочный F-тест для дисперсии»

В выходных данных кроме значений средних, дисперсий, числа наблюдений и числа степеней свободы df для каждой выборки присутствует вычисленное значение F-критерия (F), критическое значение одностороннего F-критерия (F критическое одностороннее) и вероятность значимости (P (F<=f) одностороннее). Значение Р стремится к 0,5 при минимальном различии дисперсий и к 0 - при максимальном различии дисперсий, когда нулевая гипотеза с огромной гарантией отвергается (см. выше).

Использование данного инструмента позволяет сразу делать заключение:

- при F < F_{критическое} - нет оснований отвергать нулевую гипотезу (в этом случае «P(F<=f) одностороннее» больше уровня значимости α.);

- при F > F_{критическое} нулевую гипотезу отвергают, делая заключение, что дисперсия первой выборки существенно больше, чем дисперсия второй, т. е., например, при переходе от первого процесса ко второму точность обработки увеличивается. (В этом случае «P(F<=f) одностороннее» меньше уровня значимости α.) Таким образом, при использовании данного F-теста рассчитывается односторонний критерий, т.е. соответствующий первому случаю проверки гипотезы. (Чтобы использовать двусторонний критерий, необходимо уровень значимости α уменьшить в два раза.)

Второй возможностью проверки равенства дисперсий является использование функции ФТЕСТ (рис. 7.7). Функция ФТЕСТ не рассчитывает для двух выборочных массивов данных (двух выборок) значения F и F_{критическое} как инструмент «Двухвыборочный F-тест для дисперсии», а только двустороннее P-значение F-теста. (В том, что в отличие от инструмента «Двухвыборочный F-тест для дисперсии» - это именно двустороннее P-значение F-теста, можно убедиться, сравнив P-значения, полученные при использовании функции ФТЕСТ и теста. Результат расчета функции ФТЕСТ окажется равен удвоенному значению P (F<=f) соответствующего «Двухвыборочного F-теста для дисперсии», проведённого для той же пары выборок.)

Таким образом, функция ФТЕСТ предназначена для второго случая проверки нулевой гипотезы, когда альтернативная гипотеза двусторонняя H₁: D[X] ≠ D[Y] (несмотря на надпись об односторонней вероятности сходства двух совокупностей на рис. 7.7). Поскольку эта гипотеза симметрична, неважно, какая из сравниваемых дисперсий больше, - в отличие от F-теста результат расчёта не будет зависеть от того, бόльшая или меньшая выборка будет располагаться в аргументе «Массив 1» (см. рис. 7.7).

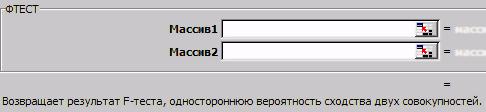
Рис. 7.7. Аргументы функции ФТЕСТ

Если рассчитанное с помощью функции ФТЕСТ значение превышает удвоенный принятый уровень значимости (α = 0, 05), делается заключение о том, что нет оснований отвергать нулевую гипотезу о равенстве дисперсий. Наоборот, если односторонняя вероятность однородности дисперсий меньше удвоенного принятого уровня значимости, нулевую гипотезу о равенстве дисперсий отвергают, т.е. установлено существенное различие в результатах двух процессов или в точности двух методов измерений. Данный результат должен стать основанием для организационных мероприятий по совершенствованию технологии производства или метода измерения.