Атомы в узлах кристаллической решётки находятся в непрерывном колебательном движении. А. Эйнштейн в 1907 г. при разработке теории теплоёмкости твёрдого вещества допустил, что колебания атомов являются гармоническими, а, следовательно, атомы можно уподобить гармоническим осцилляторам. Согласно квантовой теории М. Планка, гармонические осцилляторы могут обмениваться между собой энергией, величина которой кратна некоторой фундаментальной энергетической единице 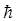 , тогда соответственно:
, тогда соответственно:
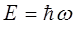
данное соотношение, с учётом выражений:
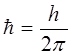
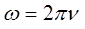
можно представить далее к виду:
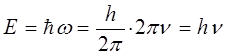
таким образом, имеем:
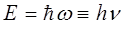
Поскольку энергия каждого из осцилляторов состоит из n -го числа квантов, тогда:
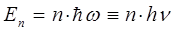
Согласно закону Больцмана, вероятность 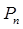 того, что энергия излучения имеет величину
того, что энергия излучения имеет величину 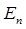 , определяется выражением вида:
, определяется выражением вида:
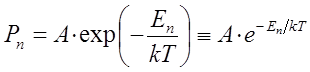
где 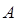 - нормировочный множитель. Поскольку:
- нормировочный множитель. Поскольку:
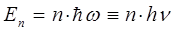
тогда соответственно:
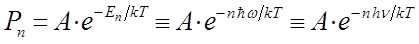
Нормировочный множитель можно найти, исходя из условия, что сумма всех вероятностей 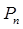 должна быть равна единице, т.е.
должна быть равна единице, т.е.
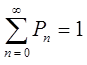
учитывая, что:
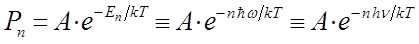
имеем соответственно:
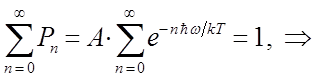
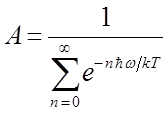
На основании проделанных выше выкладок, приходим к выражению для вероятности 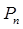 вида:
вида:
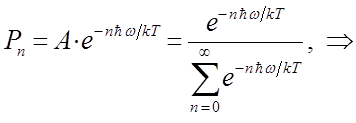
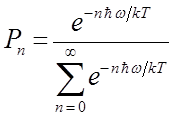
Пусть мы можем измерить значения энергии данной спектральной составляющей излучения в данный момент времени. Произведём через равные промежутки времени  достаточно большое число измерений
достаточно большое число измерений  . Для того чтобы получить среднее значение энергии, суммируем полученные результаты
. Для того чтобы получить среднее значение энергии, суммируем полученные результаты  измерений и разделим полученную сумму на число измерений. Тогда очевидно, при достаточно больших
измерений и разделим полученную сумму на число измерений. Тогда очевидно, при достаточно больших  , количество измерений
, количество измерений  будет равно:
будет равно:
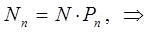

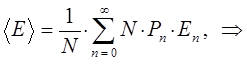
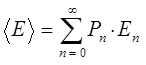
Таким образом, среднее значение энергии излучения 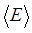 с частотой
с частотой 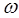 будет определяться выражением вида:
будет определяться выражением вида:
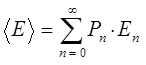
учитывая, что:
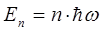
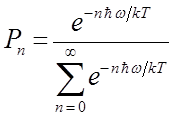
будем иметь соответственно:
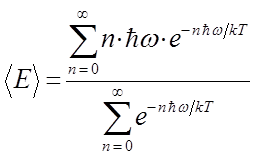
примем:
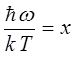
тогда после подстановки получим:
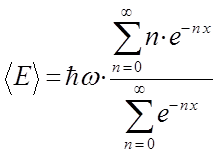
Значение знаменателя определяется формулой:
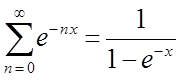
т.е. мы имеем ряд убывающей геометрической прогрессии. Числитель в выражении для 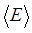 находится дифференцированием ряда убывающей геометрической прогрессии по
находится дифференцированием ряда убывающей геометрической прогрессии по 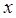 . Имеем тогда соответственно:
. Имеем тогда соответственно:
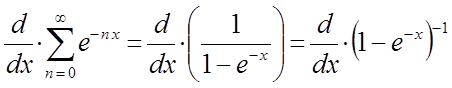
приведём полученное выше выражение к наиболее удобному для операции дифференцирования виду:
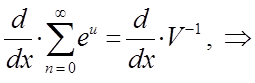
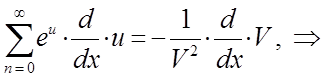
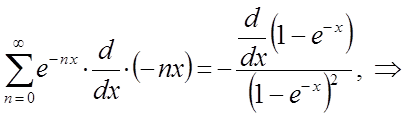
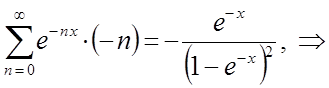
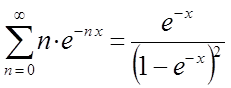
Таким образом, приходим к выражению:
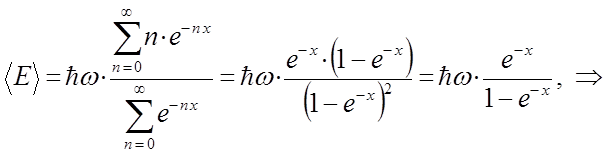
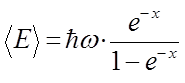
Для дальнейших выкладок, преобразуем полученное выражение для 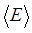 к виду:
к виду:
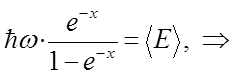
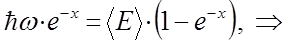
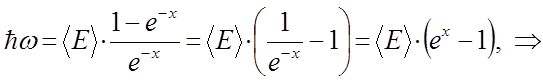
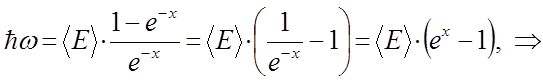
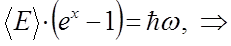
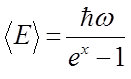
Учитывая, что:
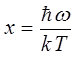
а также:
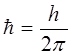
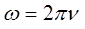
имеем:
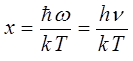
подстановка данных выражений в соответствующее уравнение для 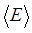 , даёт:
, даёт:
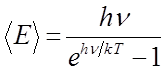
Поскольку колебания атомов в узлах кристаллической решётки имеют три степени свободы  , будем иметь соответственно:
, будем иметь соответственно:
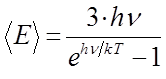
В общем случае, внутренняя энергия 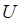 газа представляет собой кинетическую энергию всех движений частиц, тогда:
газа представляет собой кинетическую энергию всех движений частиц, тогда:
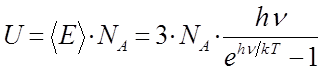
Учитывая взаимосвязь между универсальной газовой постоянной и постоянной Больцмана:
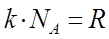
полученное уравнение:
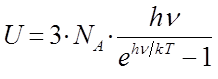
можно будет далее преобразовать к виду:
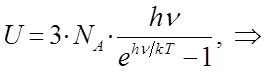
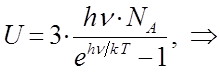
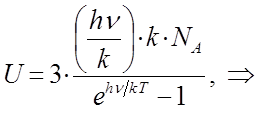
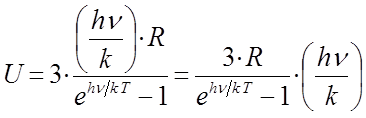
Вводя так называемую характеристическую температуру 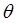 (которую называют также ещё температурой Эйнштейна), имеющей размерность температуры:
(которую называют также ещё температурой Эйнштейна), имеющей размерность температуры:
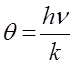
данное уравнение:
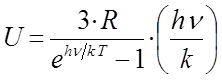
можно будет свести к ещё к более компактному виду:
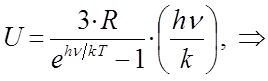
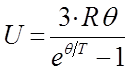
Взяв производную от выражения для внутренней энергии 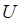 по температуре, будем иметь соответственно:
по температуре, будем иметь соответственно:
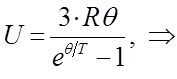
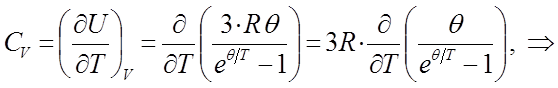
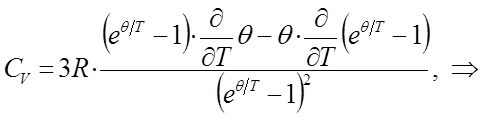
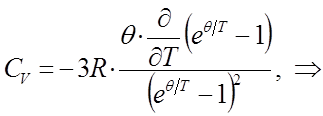
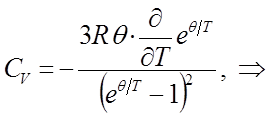
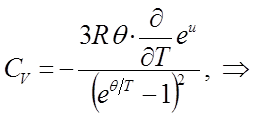
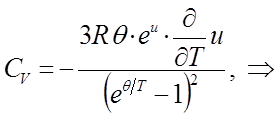
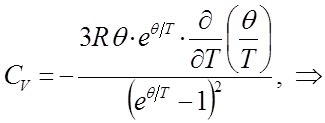
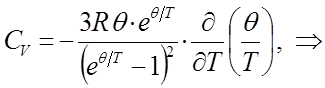
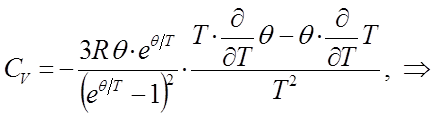
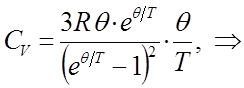
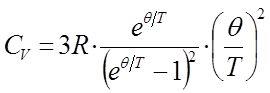
и таким образом, в ходе проделанных выкладок мы пришли к выражению:
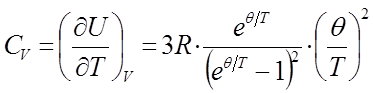
его можно также представить к виду:
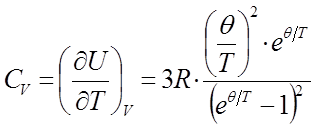
Введём величину функции теплоёмкости Эйнштейна 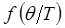 , тогда соответственно выражение для величины изохорной теплоёмкости
, тогда соответственно выражение для величины изохорной теплоёмкости 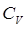 с учётом приведенных выше соотношений можно будет записать в виде:
с учётом приведенных выше соотношений можно будет записать в виде:
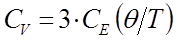
здесь:
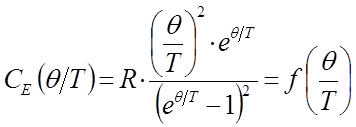
В общем случае функция 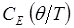 есть та часть теплоёмкости твёрдого тела, которая приходится на одну степень свободы колебательного движения.
есть та часть теплоёмкости твёрдого тела, которая приходится на одну степень свободы колебательного движения.
Поскольку 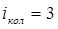 , тогда выражение для изохорной теплоёмкости
, тогда выражение для изохорной теплоёмкости 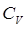 может быть записано через
может быть записано через 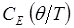 :
:
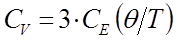
Из уравнения для изохорной теплоёмкости  :
:
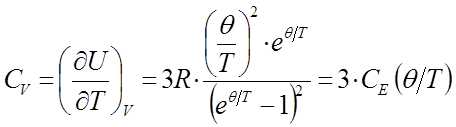
следует, что при 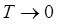 , величина
, величина 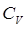 также будет стремиться к нулю
также будет стремиться к нулю 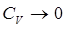 .
.
Действительно, нетрудно заметить, что:
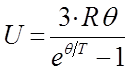
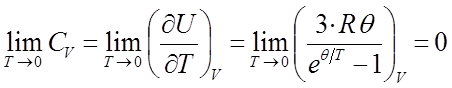
При увеличении же температуры, и стремлении последней к максимуму 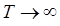 , значение изохорной теплоёмкости
, значение изохорной теплоёмкости 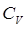 будет стремиться к своему предельному значению
будет стремиться к своему предельному значению 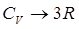 , что очень хорошо видно из следующих рассуждений. Для этих целей необходимо разложить
, что очень хорошо видно из следующих рассуждений. Для этих целей необходимо разложить 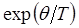 в ряд Маклорена:
в ряд Маклорена:
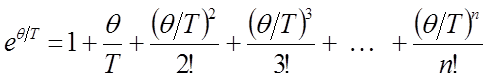
достаточно очевидно, что полученный разложением 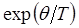 ряд при
ряд при 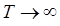 можно ограничить первыми двумя членами:
можно ограничить первыми двумя членами:
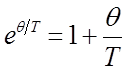
тогда подстановка полученного выражения для 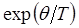 в выражение для внутренней энергии в пределе, когда
в выражение для внутренней энергии в пределе, когда 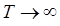 даст искомое предельное значение, т.е.
даст искомое предельное значение, т.е.
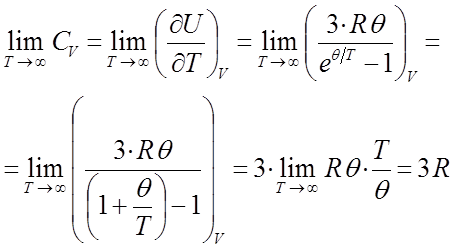
Таким образом, в ходе проделанных выкладок мы пришли к выводу, что при 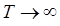 значение изохорной теплоёмкости
значение изохорной теплоёмкости 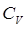 будет стремиться к своему предельному значению
будет стремиться к своему предельному значению 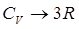 :
:
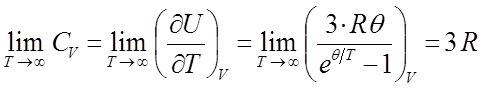
Полученное выражение для 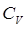 , представляет собой правило Дюлонга и Пти:
, представляет собой правило Дюлонга и Пти:
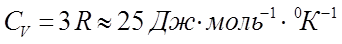
Дальнейшее развитие квантовой теории теплоёмкости твёрдого тела получило развитие в работах Дебая и ряда других учёных.
 2015-03-22
2015-03-22 525
525








