Задание 1. Вычислите пределы функций:
1.1) 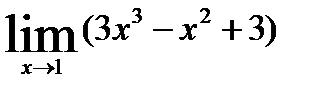 1.2)
1.2) 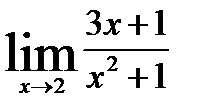 1.3)
1.3) 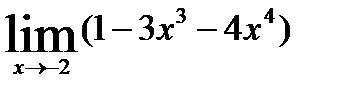 1.4)
1.4) 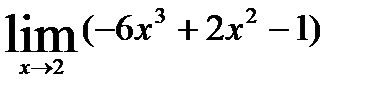
1.5) 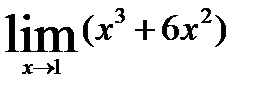
2.1) 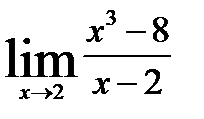 2.2)
2.2) 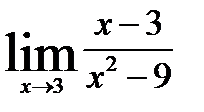 2.3)
2.3) 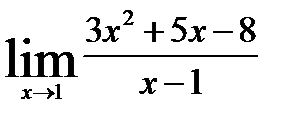 2.4)
2.4) 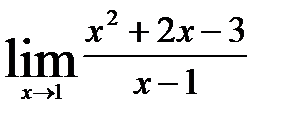
2.5) 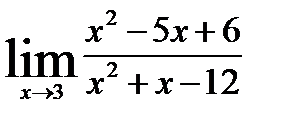
3.1) 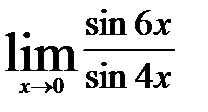 3.2)
3.2) 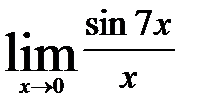 3.3)
3.3) 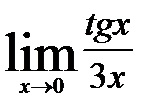 3.4)
3.4) 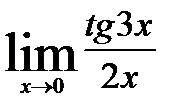 3.5)
3.5) 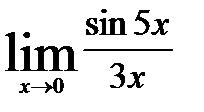
4.1) 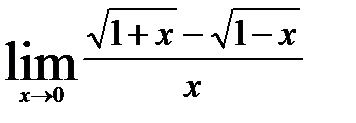 4.2)
4.2) 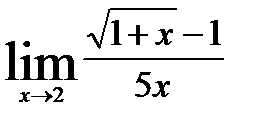 4.3)
4.3) 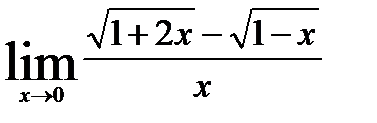
4.4) 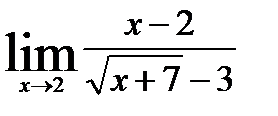 4.5)
4.5) 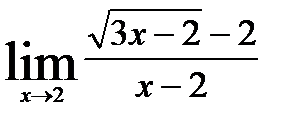
5.1) 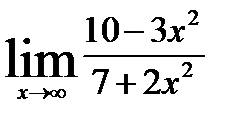 5.2)
5.2) 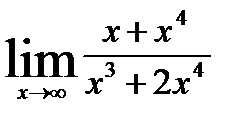 5.3)
5.3) 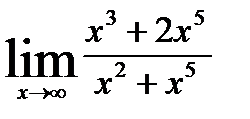 5.4)
5.4) 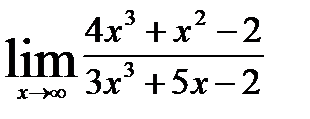
5.5) 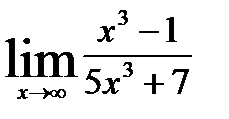
Задание 2. Найдите производную функции 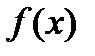 в точке
в точке 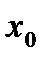 ,если:
,если:
1) 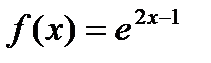 в точке
в точке 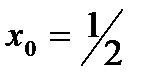
2) 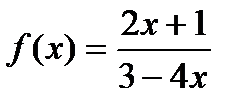 в точке
в точке 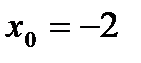 .
.
3) 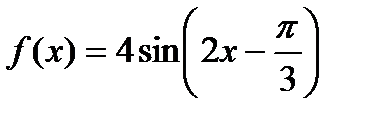 в точке
в точке 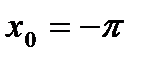 .
.
4) 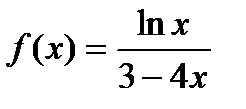 в точке
в точке 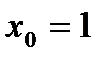 .
.
5) 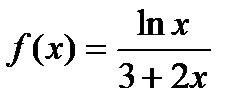 в точке
в точке 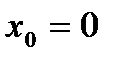 .
.
Задание 3. Вычислите 1-е производные функций:
1.1) 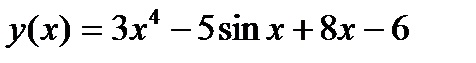 1.2)
1.2) 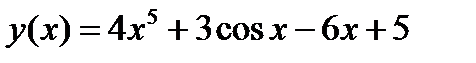
1.3) 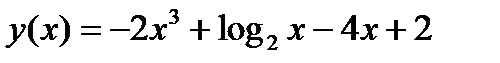 1.4)
1.4) 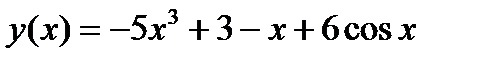
1.5) 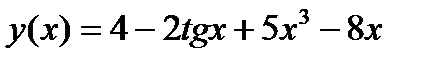
2.1) 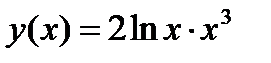 2.2)
2.2) 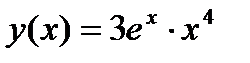 2.3)
2.3) 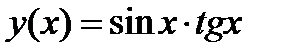 2.4)
2.4) 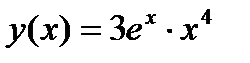
2.5) 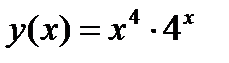
3.1) 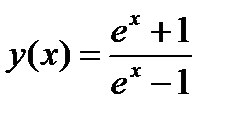 3.2)
3.2) 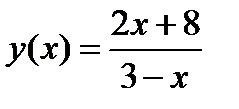 3.3)
3.3)  3.4)
3.4) 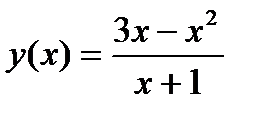
3.5) 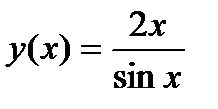
4.1) 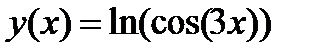 4.2)
4.2) 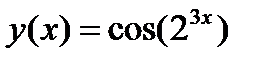 4.3)
4.3) 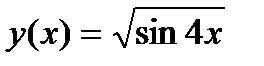
4.4) 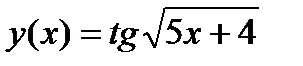 4.5)
4.5) 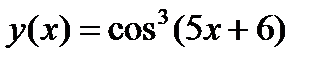
Задание 4. Найдите 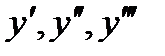 , если:
, если:
1) 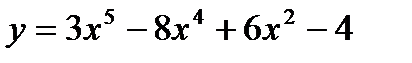
2) 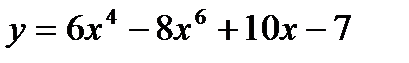
3) 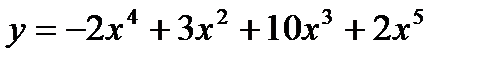
4) 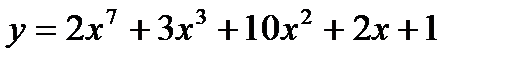
5) 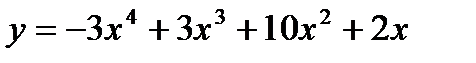
Задание 5. Для функции z(x,y) двух переменных вычислите частные производные первого и второго порядка и полные дифференциалы первого и второго порядка:
1.1) 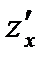 1.2)
1.2) 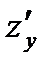 1.3)
1.3) 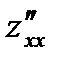 1.4)
1.4) 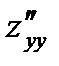 1.5)
1.5) 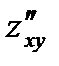 и
и 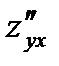 1.6)
1.6) 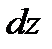 1.7)
1.7) 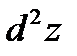 , если:
, если:
1) 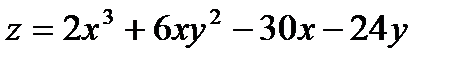
2) 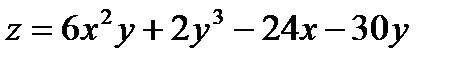
3) 
4) 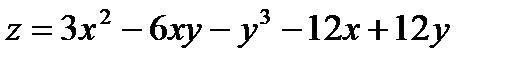
5) 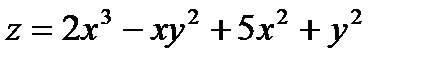
6) 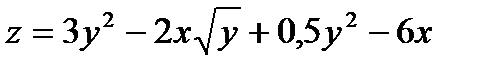
7) 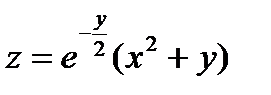
Вопросы для самоконтроля
1. Дайте определение производной.
2. Всякая ли непрерывная функция дифференцируема?
3. Найти производную функции у=х2 -3х по определению.
4. Что называется производной второго порядка?
5. В чем состоит геометрический смысл производной?
6. В чем состоит физический смысл производных I и II порядков?
7. Что называется дифференциалом функции?
8. Для какой функции ее дифференциал в каждой точки совпадает с приращением?
9. В чем заключается правило дифференцирования сложной функции?
 2015-03-22
2015-03-22 467
467








