1. 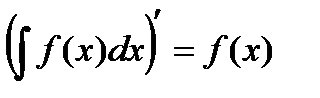 2.
2. 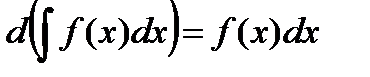 3.
3. 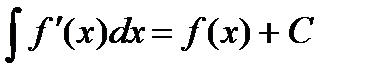 4.
4. 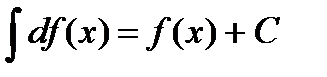
5. 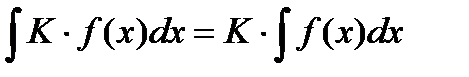 6.
6. 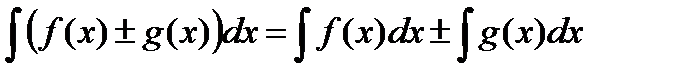
Таблица интегралов.
1. 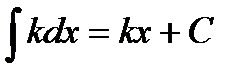 2.
2. 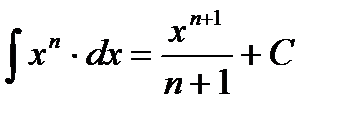 3.
3. 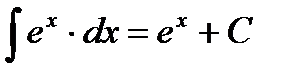 4.
4. 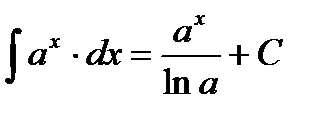
5. 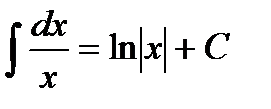 6.
6. 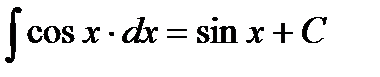 7.
7. 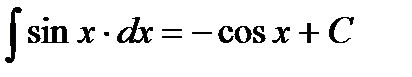 8.
8. 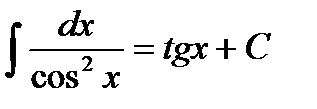
9. 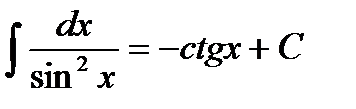 10.
10. 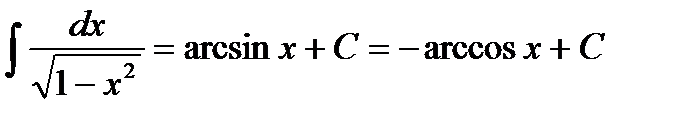
11. 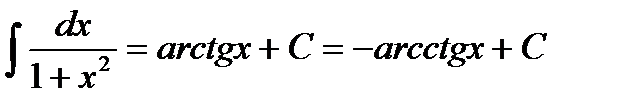
Определенный интеграл.
Определение 3. Если функция 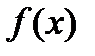 непрерывна на промежутке [a;b] числовой оси, содержащей точки x=a и x=b, то разность значений
непрерывна на промежутке [a;b] числовой оси, содержащей точки x=a и x=b, то разность значений 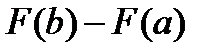 для функции
для функции 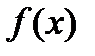 называется определенным интегралом от функции
называется определенным интегралом от функции 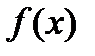 от a до b.
от a до b. 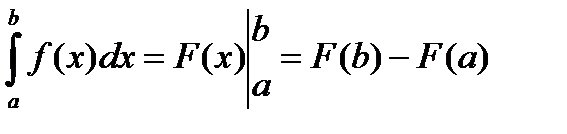 - формула Ньютона – Лейбница
- формула Ньютона – Лейбница
а- нижний предел интегрирования, в- верхний передел интегрирования
Пример: 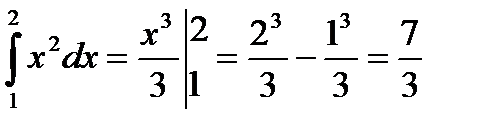
Свойства определенного интеграла.
1) 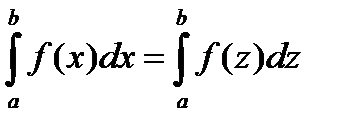 ; 2)
; 2) 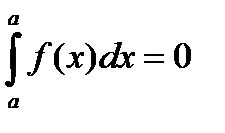 ; 3)
; 3) 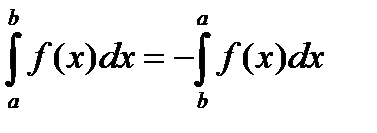
4) если 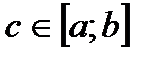 , то
, то 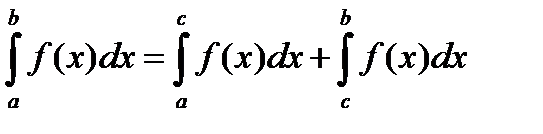 ; 5)
; 5) 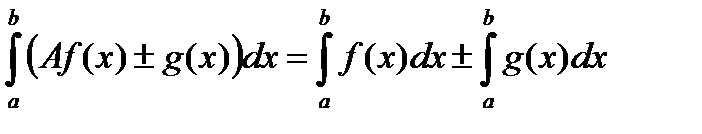
6) если 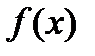 - четная непрерывная функция, то
- четная непрерывная функция, то 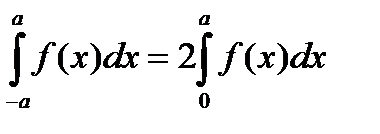
если 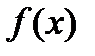 - нечетная непрерывная функция, то
- нечетная непрерывная функция, то 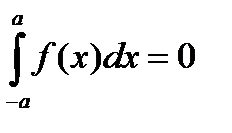
7) 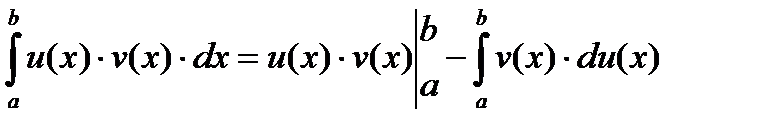
 2015-03-22
2015-03-22 389
389








