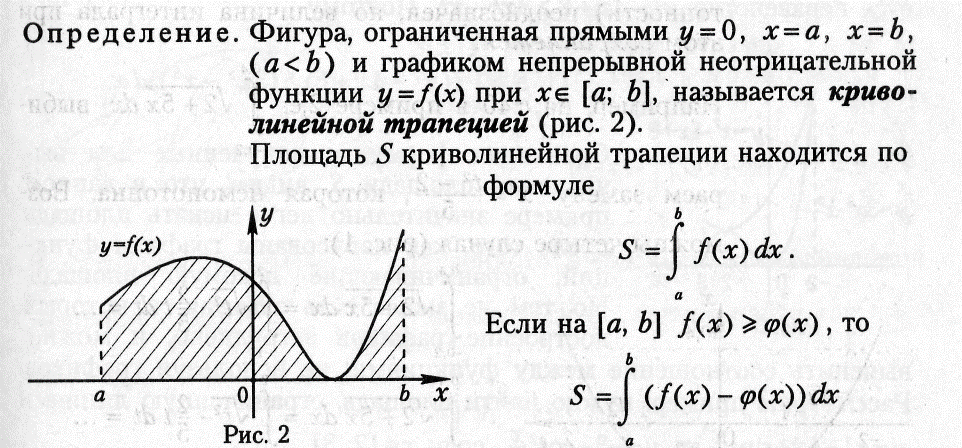
Задача. Найдите площадь фигуры, ограниченной графиком функции f(x) = x3 – 3x и осью абсцисс.
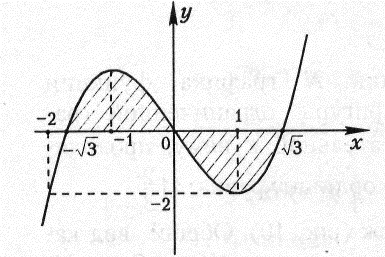 1. Построю график функции f(x) = x3 – 3x и заштрихую получившуюся фигуру.
1. Построю график функции f(x) = x3 – 3x и заштрихую получившуюся фигуру.
2. Выберу формулу для вычисления площади фигуры.
S = S1 +S2, 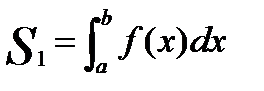
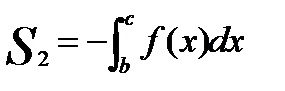
3. Рассчитаю пределы интегрирования. Пределами интегрирования будут абсциссы точек пересечения графика функции f(x) = x3 – 3x с осью абсцисс.
x3 – 3x = 0
x (x2 – 3) = 0
x = 0 или x2 – 3 = 0
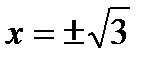 Итак, а =
Итак, а = 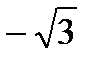 , в = 0, с =
, в = 0, с = 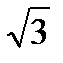
4. Подставлю уравнение функции f(x) = x3 – 3x и пределы интегрирования в формулу и вычислю определенный интеграл.
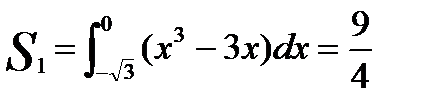 ;
; 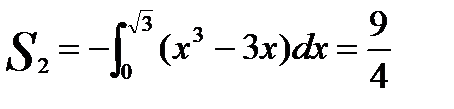
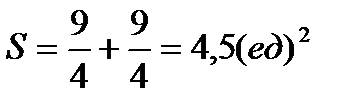
Ответ: 4,5 (ед)2
2. Объем тела вращения. 3. Площадь поверхности вращения 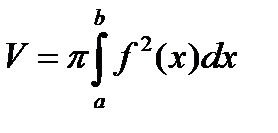
4. Длина дуги плоской кривой. 
 1. Построю график функции f(x) = x3 – 3x и заштрихую получившуюся фигуру.
1. Построю график функции f(x) = x3 – 3x и заштрихую получившуюся фигуру.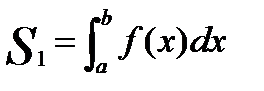
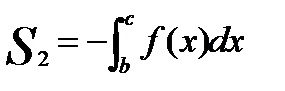
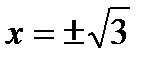 Итак, а =
Итак, а = 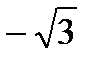 , в = 0, с =
, в = 0, с = 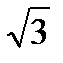
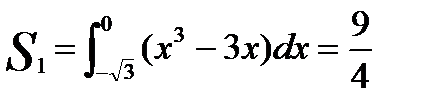 ;
; 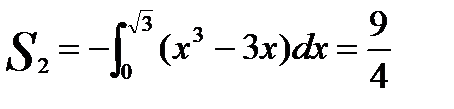
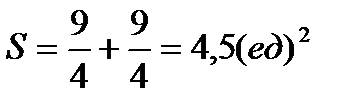
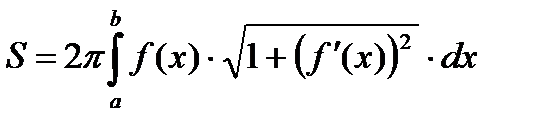
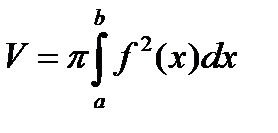
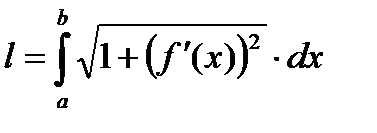
 2015-03-22
2015-03-22 1303
1303








