Рассмотрим кривую 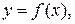 функция
функция 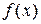 непрерывна при
непрерывна при 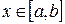 и
и 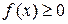 . Если ограниченную этой кривой криволинейную трапецию вращать вокруг оси
. Если ограниченную этой кривой криволинейную трапецию вращать вокруг оси 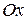 , получим тело вращения. В каждом его сечении плоскостью, перпендикулярной оси вращения, получаем круг радиуса
, получим тело вращения. В каждом его сечении плоскостью, перпендикулярной оси вращения, получаем круг радиуса 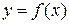 , площадь которого
, площадь которого 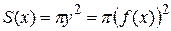 . Значит, по формуле (1) объём тела вращения равен
. Значит, по формуле (1) объём тела вращения равен
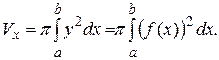 (2)
(2)
Пример 4. Вычислить объём кругового конуса c радиусом основания 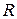 и высотой
и высотой 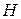 .
.
Совместим ось 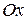 с осью конуса, считая вершину конуса начальной точкой, тогда
с осью конуса, считая вершину конуса начальной точкой, тогда 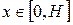 . Проведём через ось секущую плоскость и запишем уравнение прямой – образующей конуса, которая проходит через точки
. Проведём через ось секущую плоскость и запишем уравнение прямой – образующей конуса, которая проходит через точки 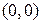 и
и 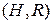 :
:
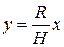 .
.
По формуле (2) получаем знакомый результат:
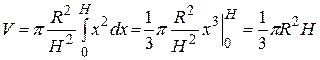 .
.
Пример 5. Вычислить объём тела, образованного вращением вокруг оси 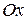 фигуры, ограниченной дугами парабол
фигуры, ограниченной дугами парабол 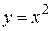 и
и 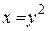 .
.
Параболы пересекаются в точках 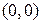 и
и 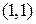 , значит,
, значит, 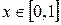 . Обозначим
. Обозначим 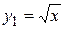 ,
, 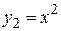 ,
, 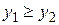 . В соответствии с формулой (2) находим
. В соответствии с формулой (2) находим
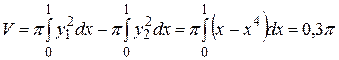 .
.
Пример 6. Найти объём общей части параболоида вращения 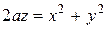 и сферы
и сферы 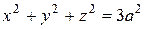 .
.
Каждое из этих тел есть тело вращения вокруг оси 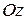 . Решая систему
. Решая систему
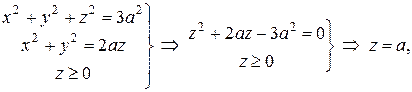
получаем, что пересечение данных поверхностей происходит по плоскости 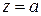 . При
. При 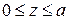 (от вершины параболоида до его встречи со сферой) круги, лежащие в перпендикулярных оси
(от вершины параболоида до его встречи со сферой) круги, лежащие в перпендикулярных оси 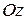 сечениях тела, имеют квадраты радиусов
сечениях тела, имеют квадраты радиусов 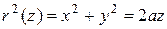 . При
. При 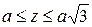 (от встречи параболоида со сферой до высшей точки сферы) квадрат радиуса равен
(от встречи параболоида со сферой до высшей точки сферы) квадрат радиуса равен 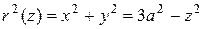 .
.
Поэтому
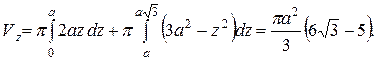
Если криволинейную трапецию, ограниченную кривой 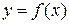 (функция
(функция 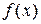 однозначна при
однозначна при 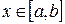 ,
, 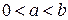 ), вращать вокруг оси
), вращать вокруг оси 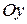 , получим тело вращения, объём которого определяется по формуле
, получим тело вращения, объём которого определяется по формуле
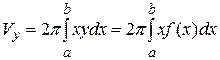 (3)
(3)
Заметим, что при вычислении объёма 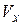 тело «набирается» из элементарных цилиндров с радиусом
тело «набирается» из элементарных цилиндров с радиусом 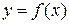 и толщиной
и толщиной 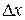 , нанизанных на ось вращения
, нанизанных на ось вращения 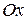 . Тогда элементарный объём равен
. Тогда элементарный объём равен 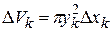 и выражение
и выражение 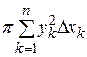 есть интегральная сумма для непрерывной функции
есть интегральная сумма для непрерывной функции 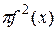 . А при вычислении объёма
. А при вычислении объёма 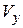 тело «набирается» из концентрических тонкостенных цилиндров с радиусом
тело «набирается» из концентрических тонкостенных цилиндров с радиусом 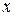 , высотой
, высотой 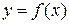 и толщиной
и толщиной 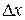 . Объём такого цилиндра можно приближенно считать равным объёму прямоугольного параллелепипеда с размерами
. Объём такого цилиндра можно приближенно считать равным объёму прямоугольного параллелепипеда с размерами 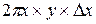 , т.е. элементарный объём
, т.е. элементарный объём 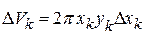 , тогда выражение
, тогда выражение 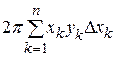 – интегральная сумма для непрерывной функции
– интегральная сумма для непрерывной функции 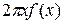 .
.
Пример 7. Вычислить объём тела, полученного при вращении синусоиды 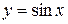 ,
, 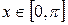 а) вокруг оси
а) вокруг оси 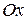 , б) вокруг оси
, б) вокруг оси 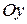 .
.
а) По формуле (2) находим:
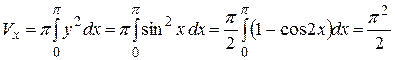 .
.
б) По формуле (3) находим:
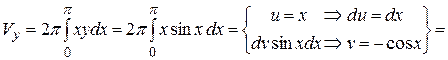
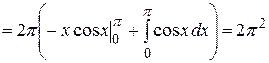 .
.
Пример 8. Вычислить объём тела, полученного при вращении окружности 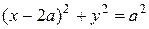 а) вокруг оси
а) вокруг оси 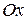 , б) вокруг оси
, б) вокруг оси 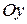 .
.
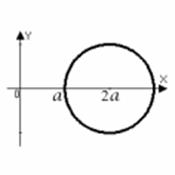
а) Задано уравнение окружности радиуса 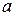 со смещенным в точку
со смещенным в точку 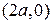 центром, т.е.
центром, т.е. 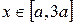 . При вращении окружности вокруг оси
. При вращении окружности вокруг оси 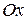 получаем шар, объём которого находим по формуле (2):
получаем шар, объём которого находим по формуле (2):
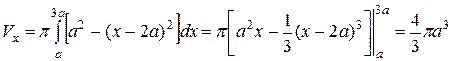
| 
|
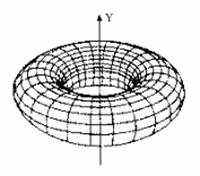
б) Первый способ. При вращении смещенной окружности вокруг оси 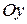 получаем тор. Полагая в формуле (3)
получаем тор. Полагая в формуле (3) 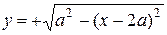 ,
, 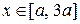 , где
, где 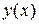 – однозначная функция (вращаем верхнюю половину окружности), найдем объем половины тора:
– однозначная функция (вращаем верхнюю половину окружности), найдем объем половины тора:
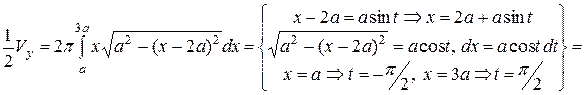
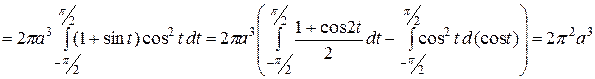 .
.
В силу симметрии 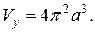
Второй способ. Рассмотрим положительные функции 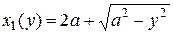 и
и 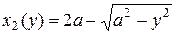 (правая и левая половина окружности), здесь
(правая и левая половина окружности), здесь 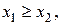
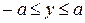 . Если в формуле (2) поменять местами переменные
. Если в формуле (2) поменять местами переменные 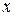 и
и 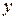 , то
, то
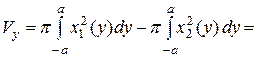
 2015-05-05
2015-05-05 1908
1908








