Исходя из разговорной практики, мы знаем, что, имея высказывания А и В, можно построить высказывания: не А (неверно, что А); А и В; А или В; если А, то В (из А следует В); А только и только тогда, когда В (А эквивалентно В, А тождественно В). Эти высказывания, в отличие от элементарных, естественно назвать сложными, поскольку они уже наделены структурой. Однако они так же, как и простые, могут принимать только два возможных значения: И либо Л.
Пример 3. Для составного высказывания «Пришла весна, и грачи прилетели» выделите простые, обозначив каждое из них буквой; запишите с помощью логических операций составное высказывание:
Решение: Обозначим через A-«пришла весна»; а через B- «грачи прилетели». Тогда высказывание С -«Пришла весна, и грачи прилетели» запишем так: С= А  B. Ответ: С= А
B. Ответ: С= А  B.
B.
Пример 4. Определить значение истинности высказываний:
1) «7 является простым числом, или 19 является простым числом». Данное высказывание является сложным, поэтому обозначим А – «7 является простым числом», a В – «19 является простым числом». Имеем, что А=1, В=1. Составим формулу АÚВ и, используя таблицу истинности, найдем логическое значение формулы. Получим АÚВ= 1.
2) «2 + 3 = 6 и Архангельск расположен на Северной Двине». Данное высказывание является сложным, поэтому обозначим А – «2+ 3 = 6», а В-«Архангельск расположен на Северной Двине». Имеем, что А = 0, В = 1. Составим формулу АÙВ и, используя таблицу истинности, найдем логическое значение формулы. Получим АÙВ =0.
3) «Если 12 делится на 6, то 12 делится на 4». Данное высказывание является сложным, поэтому обозначим А- «12 делится на 6», а В – «12 делится на 4». Имеем, что А= 1,В=1. Составим формулу А®В и, используя таблицу истинности, найдем логическое значение формулы. Получим А®В= 1.
4) «11 делится на 3 тогда и только тогда, когда 20 делится на 5». Данное высказывание является сложным, поэтому обозначим А – «11 делится на 3», а В- «20 делится на 5». Имеем, что А=0, В = 1. Составим формулу А«В и, используя таблицу истинности, найдем логическое значение формулы. Получим А«В= 0.
Пример 5. Если будет холодно (А), то я надену теплое пальто (В), если рукав будет починен (С). Завтра будет холодно, а рукав не будет починен. Следует ли отсюда, что я не надену теплое пальто?
Решение. Посылки нашего рассуждения символически записываются следующим образом: А®(С®В), АÙ 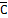 .Следует ли отсюда утверждение В? Предположим, что высказывание В ложно, в то время как все посылки являются истинными высказываниями. Тогда В =0, а В = 1. Значит, первая посылка А®(С®В), действительно истинна, а вторая будет истинной, если А истинно, а С ложно. Таким образом, ситуация, когда все посылки истинны, а высказывание В ложно, вполне возможна. Это означает, что высказывание В не следует из данных посылок.
.Следует ли отсюда утверждение В? Предположим, что высказывание В ложно, в то время как все посылки являются истинными высказываниями. Тогда В =0, а В = 1. Значит, первая посылка А®(С®В), действительно истинна, а вторая будет истинной, если А истинно, а С ложно. Таким образом, ситуация, когда все посылки истинны, а высказывание В ложно, вполне возможна. Это означает, что высказывание В не следует из данных посылок.
Множество. Способы задания множеств.
Одним из основных исходных понятий математики является понятие множества и его элементов. Множество состоит из элементов. Множества обозначаются большими латинскими буквами: A; B; C..., а их элементы - малыми буквами: a,b,c,…
Если a является элементом множества A или, что то же самое, a принадлежит множеству A, то применяют запись aÎA; в противном случае пишут aÏA.
Два множества A и B равны (A=B), если они состоят из одних и тех же элементов. Если множества A и B не равны, то применяется запись A ¹ B.
Множество, содержащее конечное число элементов, называется конечным, в противном случае множество называется бесконечным. Конечное множество, содержащее n элементов, называется n-множеством.
Множество, не содержащее элементов, называется пустым и обозначается Æ.
Предположим, что все множества, которые будут рассмотрены в этой главе, являются подмножествами некоторого множества U, называемого универсальным множеством.
а б
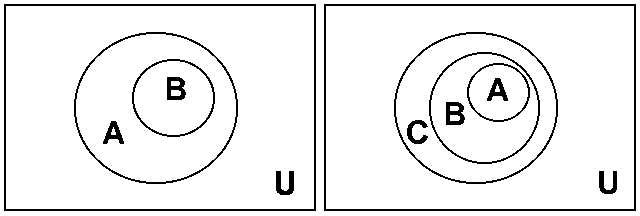
Рис. 1.1.
Если каждый элемент а множества В, аÎВ, является элементом множества А, аÎА, то В называется подмножеством множества А (рис. 1.1, а). Этот факт записывается с помощью знака включения Í следующим образом: ВÍА.
Свойства включения
1. АÍ А;
2. если АÍ В и ВÍС, то АÍС (рис. 1.1, б);
3. из двух включений ВÍА и АÍ В следует, что А=В.
Принято считать, что пустое множество является подмножеством любого множества.
Если ВÍ А и при этом В¹А, то этому соответствует запись ВÌ А и В называется собственным подмножеством А. В решении примера 1.1 все множества, кроме последнего, являются собственными подмножествами множества А.
Для описания множества A, состоящего из элементов a1,a2,...,an,... обычно применяется запись A={a1,a2,...,an,...}, причём порядок элементов в фигурных скобках не имеет значения; обычно он определяется соображениями наглядности.
Пример 1. В записи множества первых n натуральных чисел Nn={1,2,...,n} удобно располагать числа в возрастающем порядке, хотя при этом надо иметь в виду, что N3 ={1,2,3}={2,1,3}={3,2,1}.
Другой способ задания множества состоит в описании свойств, однозначно определяющих принадлежность элементов данному множеству. Такому способу задания множества соответствует запись: A ={a/a обладает свойством P(a)}.
Пример 2. Множество чётных чисел M может быть задано так: M={i / i - целое число, которое делится на 2 без остатка}.
В случае описания множества с помощью некоторого свойства необходимо следить за тем, чтобы каждый элемент был чётко определён. Так, например, недостаточно чётким является определение множества А как множества слов русского языка, если нет ссылки на один из толковых словарей.
Возможно также рекурсивное задание множества, при котором осуществляется последовательное описание элементов через предыдущие. Например, множество натуральных чисел рекурсивно можно задать так: N={i / если целое iÎN, то i+1ÎN, i ³ 1}.
Операции над множествами. Законы действий над множествами.
Объединением двух множеств А и В называется множество вида:
AÈB ={a / aÎ A или aÎ B}(рис. 1.2, а).
Пересечением двух множеств А и В называется множество вида:
AÇB={a / aÎ A и aÎ B} (рис. 1.2, б).
Если множества А и В не имеют общих элементов, то AÇB=Æ.
а б
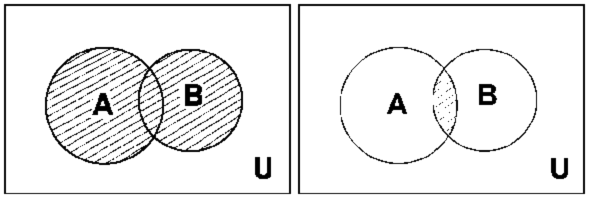
Рис. 1.2.
Свойства операций объединения и пересечения
1. AÈB = ВÈА, AÇB = ВÇА (коммутативность);
2. (AÈB)ÈС = AÈ(BÈС), (AÇB)ÇС = AÇ(BÇС) (ассоциативность).
3. Объединение и пересечение связаны законами дистрибутивности:
AÇ(BÈC)= (AÇB) È (AÇС); AÈ(BÇC)= (AÈB) Ç (AÈС).
По свойству 3 операции включения следует равенство правой и левой частей доказываемого равенства.
Для операции объединения множеств нейтральным является пустое множество Æ, а для операции пересечения множеств - универсальное множество U.
Разность множеств А и В определяется следующим образом:
A\B ={a / aÎA и aÏB} (рис. 1.3, а).
Разность не обладает свойством коммутативности; эта операция также не является и ассоциативной.
Пользуясь понятием универсального множества, можно определить дополнение  к множеству А, как разность вида:
к множеству А, как разность вида: 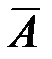 = U \ A (рис. 1.3, б).
= U \ A (рис. 1.3, б).
а) б)
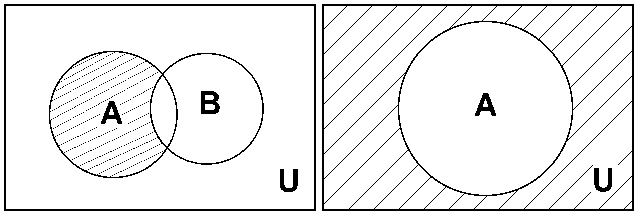
Рис. 1.3.
Пример 3. Пусть в качестве универсального множества выступает множество целых чисел Z и пусть А - это множество всех чётных чисел. Тогда 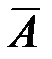 - это множество всех нечётных чисел.
- это множество всех нечётных чисел.
Операции объединения, пересечения и дополнения множеств связаны между собой законами де Моргана:
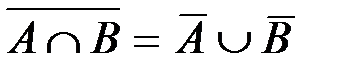 ,
, 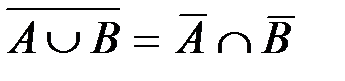 .
.
 2015-03-22
2015-03-22 5976
5976








