Краткие теоретические сведения. Федеральное агентство железнодорожного транспорта

Федеральное агентство железнодорожного транспорта

Государственное образовательное учреждение

Высшего профессионального образования

Иркутский государственный университет путей сообщения

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению лабораторной работы «Определение коэффициентов электростатической индукции и частичных емкостей в системе заряженных тел»

Составитель – Саломатов В.Н.

ИРКУТСК 2011

Цель работы:

найти значения коэффициентов электростатической индукции и частичных емкостей для трех жил трехжильного кабеля.

Краткие теоретические сведения

q₁q₂q_iq_n

… …

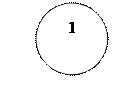j₁j₂j_ij_n

Рис. 1. Система заряженных тел. Заряженные тела 1,2, …i, … n расположены недалеко друг от друга, взаимодействуют друг с другом. j₁, j₂,....... j_n - потенциалы тел, q₁,q_2,……..q_n - заряды тел.

В системе заряженных тел потенциал каждого тела определяется не только зарядом данного тела, но также и зарядами всех остальных тел. При этом, если диэлектрическая проницаемость среды, в которой находятся эти тела, не зависит от напряженности электрического поля (ε_a = const), то потенциалы тел являются линейными функциями зарядов и наоборот. Это утверждение записывается с помощью формул, называемых формулами Максвелла (первая группа формул Максвелла):

φ₁ = α₁₁q₁ + α₁₂ q₂ + … α_1iq_i + … α_1nq_n

φ₂ = α₂₁q₁ + α₂₂ q₂ + … α_2iq_i + … α_2nq_n

……….. (1)

φ_i = α_i1q₁ + α_i2 q₂ + … α_iiq_i + … α_inq_n

………..

φ_n = α_n1q₁ + α_n2 q₂ + … α_niq_i + … α_nnq_n .

Эти формулы представляют собой систему линейных уравнений, где α_ik – коэффициенты связи между зарядами и потенциалами тел. В электротехнике эти коэффициенты называются потенциальными коэффициентами.

α_ik при i = k – собственные потенциальные коэффициенты,

α_ik при i ≠ k – взаимные потенциальные коэффициенты.

Без вывода: α_ik = α_ki .

Выразив заряды тел через потенциалы тел, получим вторую группу формул Максвелла:

q₁ = β₁₁φ₁ + β₁₂φ₂ + … β_1iφ_i + … β_1nφ_n

q₂ = β₂₁φ₁ + β₂₂φ₂ + … β_2iφ_i + … β_2nφ_n

……….

q_i = β_i1φ₁ + β_i2φ₂ + … β_iiφ_i + … β_inφ_n (2)

……….

q_n = β_n1φ₁ + β_n2φ₂ + … β_niφ_i + … β_nnφ_n .

Коэффициенты связи в этих формулах называются коэффициентами электростатической индукции.

β_ik при i = k – собственные коэффициенты электростатической индукции,

β_ik при i ≠ k – взаимные коэффициенты электростатической индукции.

Без вывода: β_ik = β_ki.

Первую и вторую группы формул Максвелла можно записать в матричном виде:

(φ) = (α)(q)

(q) = (β)(φ)

Матрицы (α) и (β) связаны соотношениями:

(β) = (α)^-1

(α) = (β)^-1 _.

То есть, если известна одна из матриц (α) или (β), то другую можно найти, транспонируя соответствующую матрицу.

Можно выразить заряды тел не через потенциалы тел (как во второй группе), а через разности потенциалов тел. Соответствующая система уравнений называется третьей группой формул Максвелла:

q₁=c₁₁(φ₁–0) + c₁₂(φ₁–φ₂) + … c_1i (φ₁–φ_i) + … c_1n(φ₁–φ_n)

q₂=c₂₁(φ₂– φ₁) + c₂₂(φ₂–0) + … c_2i (φ₂–φ_i) + … c_2n(φ₂–φ_n)

………. (3)

q_i=c_i1(φ_i– φ₁) + c_i2(φ_i–φ₂) + … c_ii (φ_i–0) + … c_in(φ_i–φ_n)

……….

q_n=c_n1(φ_n– φ₁) + c_n2(φ_n–φ₂) + … c_ni (φ_n–φ_i) + … c_nn(φ_n–0).

Коэффициенты связи c_ik называются частичными ёмкостями.

c_ik при i = k – собственные частичные ёмкости,

c_ik при i ≠ k – взаимные частичные ёмкости.

В диагональных членах этой системы уравнений содержатся разности потенциалов соответствующего тела и потенциала точки, соединённой с землёй (потенциал равен нулю).

Все три группы формул Максвелла справедливы, если ноль потенциала выбран на земле или на бесконечности (в точках, бесконечно удалённых от всех зарядов q₁, q₂, … q_i, … q_n).

Коэффициенты связи α_{ik ,} β_{ik ,} c_ik зависят от формы, размеров тел, от взаимного расположения тел (от конфигурации тел), от расстояний между телами, а также от значения диэлектрической проницаемости среды, в которой находятся эти тела. То есть совокупность этих коэффициентов является характеристикой данной конкретной системы тел (так же, как ёмкость одного или двух одинаковых тел).

Коэффициенты α_ik, β_ik, c_ik не изменятся (мало изменятся), если тела соединить произвольным образом между собой и землёй тонкими проводниками с малой ёмкостью. На этом основаны экспериментальные методы определения коэффициентов.

При определении коэффициентов электростатической индукции одно из тел заряжается, все другие соединяются с землёй (их потенциалы равны нулю). При определении частичных ёмкостей все тела соединяются между собой (их потенциалы одинаковы), и заряжаются, например, путём присоединения к положительному полюсу батареи.

В лабораторной работе в качестве системы заряженных тел используются три жилы трёхжильного кабеля. Предполагается, что эти жилы имеют большие размеры (диаметры), а их присоединение к батарее или земле осуществляется тонкими соединительными проводниками. В этом случае системы уравнений в каждой группе формул Максвелла включают в себя по три уравнения, причём в правой части каждого уравнения содержится по три слагаемых. В зависимости от способа соединения жил эти уравнения существенным образом упрощаются.

Определение β_ik при i =k

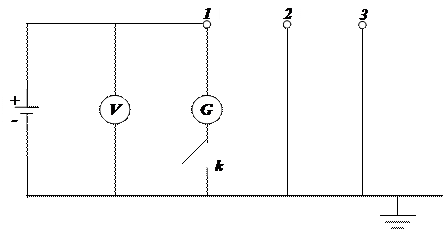Рис. 2 Принципиальная схема для определения β₁₁ .

1,2,3 – жилы трехжильного кабеля.

При соединении жил, как на Рис.2,

q₁ > 0, q₂ < 0, q₃ < 0, φ₁ >0, φ₂ = φ₃ =0.

q₁ > 0, φ₁ >0 потому, что первая жила присоединена к положительному полюсу батареи (заряжена). φ₂ = φ₃ =0 потому, что вторая и третья жилы заземлены. q₂ < 0, q₃ < 0 (несмотря на то, что φ₂ = φ₃ =0) потому, что заземленные вторая и третья жилы находятся близко к заряженной первой жиле. Электростатическое поле, существующее во всем пространстве вокруг заряженной первой жилы, индуцирует отрицательные заряды на второй и третьей жиле, притягивая их «из земли». Если бы заземленные вторая и третья жилы находились далеко от заряженной первой жилы, имело бы место φ₂ = φ₃ =0, q₂ = q₃ =0.

Используем первое уравнение второй группы при n=3, φ₂ = φ₃ =0. Видим, что при выполнении условия φ₂ = φ₃ =0 это уравнение упростилось и имеет вид

q₁ = β₁₁ φ₁ .

Отсюда

β₁₁= 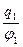. (4)

Последнее справедливо лишь в схеме на Рис.2, которую мы специально собрали для экспериментального определения β₁₁ .

φ₁ найдем по показаниям вольтметра (вольтметр показывает φ₁ = φ₁ – 0, так как одна из клемм вольтметра заземлена). q₁ найдем по показаниям гальванометра. Величина отклонения стрелки баллистического гальванометра (число делений, на которые отклоняется стрелка) прямо пропорциональна заряду, прошедшему через гальванометр за короткий промежуток времени (в лабораторной работе в момент замыкания ключа k).

То есть заряд q₁ можно найти по отклонению стрелки гальванометра после его градуировки и определения характеристики гальванометра, называемой постоянная гальванометра. Зная q₁ и φ₁, найдем β₁₁ по формуле (4).

Определение β_ik при i ≠ k

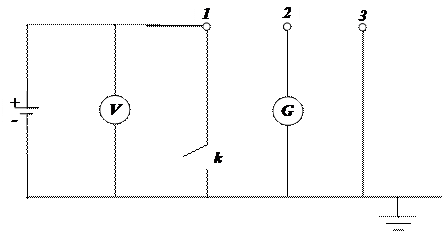Рис. 3. Принципиальная схема для определения β₂₁.

Изобразим схему, такую же, как на Рис.2, но гальванометр поместим в другое место (Рис. 3).

В этой схеме, как и в схеме, изображенной на Рис.2, q₁ > 0, φ₁>0, q₂ < 0, q₃ < 0, φ₁ = φ₃ = 0. Используем второе уравнение второй группы при n = 3 и при φ₁ = φ₃ = 0, Получим

q₂ = β₂₁ φ₁ .

β₂₁= .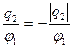

При записи последней формулы вспомним, что ранее мы обосновали наличие отрицательного заряда q₂ < 0 на второй жиле, если q₁ > 0.

φ₁ найдем по показаниям вольтметра. При замыкании ключа в схеме на Рис. 2 и на Рис. 3 заряд первой жилы q₁ за короткий промежуток времени «уйдет на землю». При этом исчезнет электрическое поле, индуцирующее заряд q₂ < 0. Таким образом, в момент замыкания ключа заряд q₂ < 0 также за короткий промежуток времени «уйдет на землю» через гальванометр.

Как и β₂₁, все β_ik при i ≠ k оказываются отрицательными.

Определение с_ik при i = k

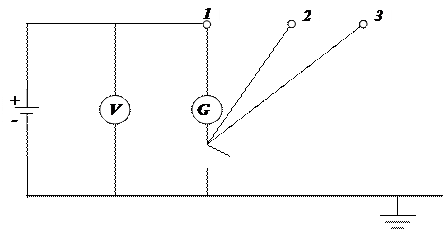Рис. 4. Принципиальная схема для определения с₁₁ .

В схеме, изображенной на Рис.4, ни одна из жил не заземляется, а все жилы соединяются между собой (в одну точку). При этом φ₁ = φ₂ = φ₃. Гальванометр расположен таким образом, чтобы в момент замыкания ключа через него проходил на землю заряд лишь одной первой жилы.

Используем первую формулу третьей группы при n=3 и при φ₁ = φ₂ = φ₃.

Получим ,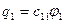

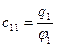. (6)

Определение с_ik при i ≠ k

Без вывода: с_ik при i ≠ k = -β_ik при i ≠ k.

Поэтому в нашем случае определять экспериментально с_ik при i ≠ k нет необходимости. Они будут равны (с обратным знаком) коэффициентам

β_ik при i ≠ k. Так как последние отрицательны, то с_ik при i ≠ k > 0.