Задание 1. Решить систему уравнений а) методом Жордана-Гаусса; б) методом модифицированных жордановых исключений. Найти все базисные решения системы.
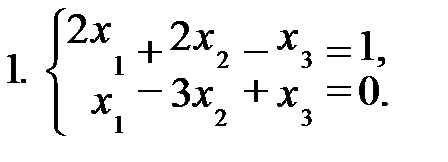 | 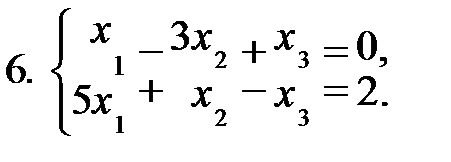 |
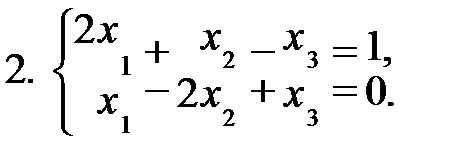 | 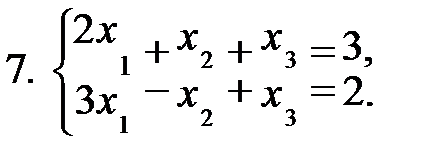 |
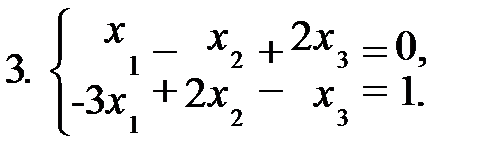 | 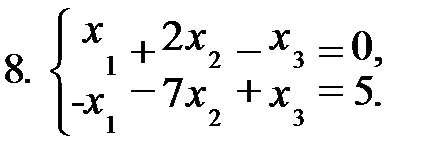 |
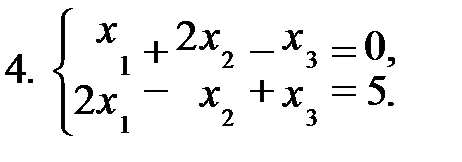 | 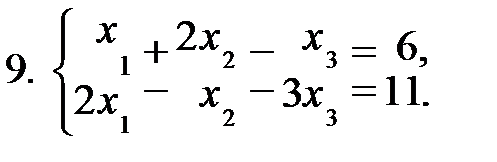 |
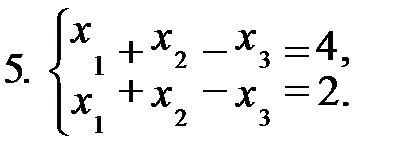 | 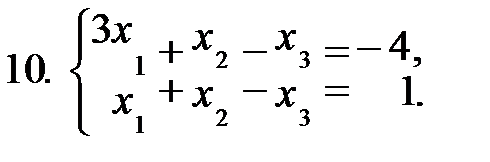 |
Задание 2. Решить систему уравнений а) по формулам Крамера; б) матричным способом.
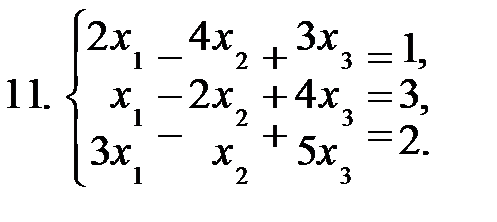 | 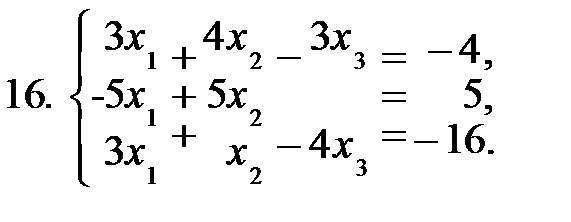 |
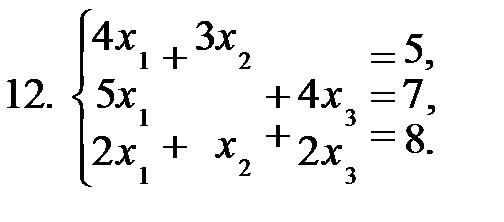 | 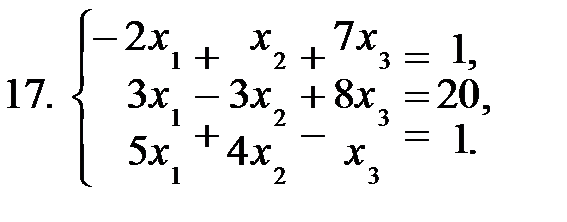 |
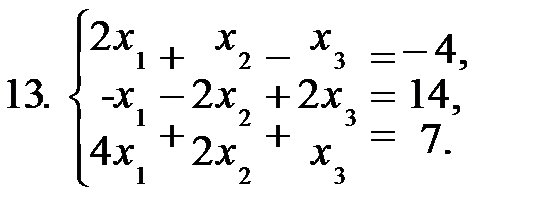 | 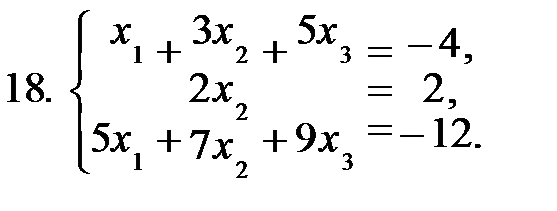 |
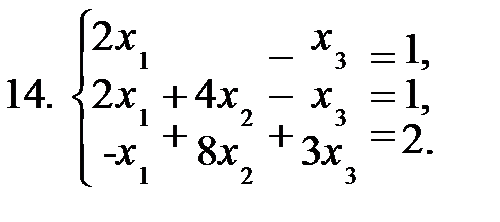 | 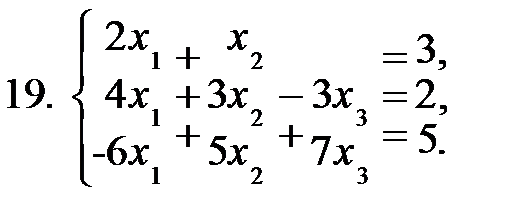 |
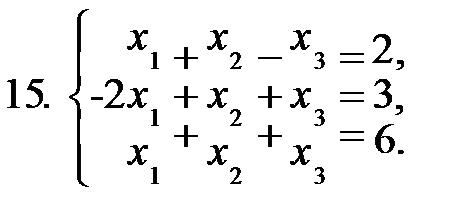 | 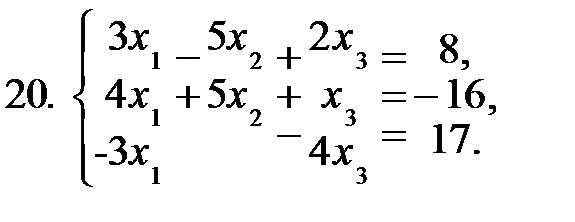 |
Задание 3. Выяснить является ли система векторов линейно зависимой или линейно независимой, в случае линейной зависимости привести пример нетривиальной линейной комбинации, равной нулевому вектору (представить один из векторов в виде линейной комбинации остальных).
21. а1 = (1; 2; 3; 4), а2 = (4; 3; 2; 1), а3 = (5; 5; 5; 5).
22. а1 = (1; 1; 1; 1), а2 = (1; 2; 3; 4), а3 = (1; 3; 3; 1).
23. а1 = (1; 3; 3; 6), а2 = (2; 3; 0; 3), а3 = (1; 2; 1; 3).
24. а1 = (1; 1; 1; 1), а2 = (1; -1; 1; -1), а3 = (2; 3; 1; 4).
25. а1 = (0; 2; 4; 6), а2 = (-1; 0; 1; 1), а3 = (2; 4; -1; 3).
26. а1 = (4; 3; 2; 1), а2 = (1; 2; 3; 4), а3 = (5; 6; 5; 0).
27. а1 = (1; 3; 2; -4), а2 = (1; 2; 0; 4), а3 = (2; 4; 0; 8).
28. а1 = (4; 3; 2; 1), а2 = (2; 3; 4; 5), а3 = (6; 6; 6; 6).
29. а1 = (1; 2; 0; 3), а2 = (2; 1; 3; 4), а3 = (1; 0; 3; -2).
30. а1 = (0; 1; 1; 2), а2 = (1; 2; 3; 1), а3 = (1; 2; 3; -4).
Задание 4. Показать, что векторы а1, а2, а3 образуют базис в R 3 базис и разложить вектор а4 по этому базису.
31. а1 = (2; 1; 3), а2 = (-4; -2; -1), а3= (3; 4; 5), а4 = (1; 3; 2).
32. а1 = (2; 1; 4), а2 = (-3; 5; 1), а3= (1; -4; -3), а4 = (2; -5; -4).
33. а1 = (2; 3; 1), а2 = (-1; 2; -2), а3= (1; 2; 1), а4 = (2; -2; 1).
34. а1 = (1; 2; 1), а2 = (2; -1; 3), а3= (3; -1; 4), а4 = (5; 1; 6).
35. а1 = (2; 2; -1), а2 = (0; 4; 8), а3= (-1; -1; 3), а4 = (1; 1; 2).
36. а1 = (1; -2; 1), а2 = (1; 1; 1), а3= (-1; 1; 1), а4 = (2; 3; 6).
37. а1 = (3; -2; 2), а2 = (-1; 1; -1), а3= (0; 1; 4), а4 = (5; 0; 15).
38. а1 = (5; 1; 4), а2 = (0; -1; 1), а3= (4; 2; 2), а4 = (1; 0; 1).
39. а1 = (2; 3; 1), а2 = (2; 2; 1), а3= (-1; -3; -2), а4 = (4; 7; 3).
40. а1 = (2; -1; 4), а2 = (1; -2; 2), а3= (-1; 2; 1), а4 = (-4; 14; 7).
Задание 5. Дана матрица А линейного оператора в 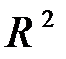 . 1). Построить матричный оператор, заданный матрицей А. 2). Найти собственные значения и собственные векторы линейного оператора (матрицы). 3). Привести квадратичную форму, заданную матрицей А в
. 1). Построить матричный оператор, заданный матрицей А. 2). Найти собственные значения и собственные векторы линейного оператора (матрицы). 3). Привести квадратичную форму, заданную матрицей А в 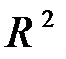 , к каноническому виду, а также найти ортонормированный базис, в котором она имеет этот вид. 4). Построить линии уровня квадратичной формы.
, к каноническому виду, а также найти ортонормированный базис, в котором она имеет этот вид. 4). Построить линии уровня квадратичной формы.
41. А= 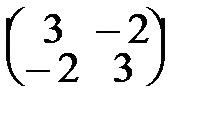 . . | 46. А= 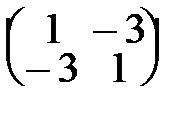 . . |
42. А= 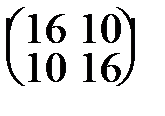 . . | 47. А= 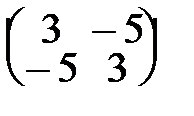 . . |
43. А= 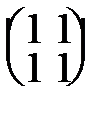 . . | 48. А= 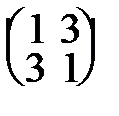 . . |
44. А= 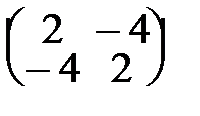 . . | 49. А= 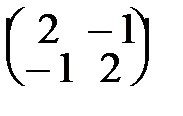 . . |
45. А= 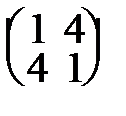 . . | 50. А= 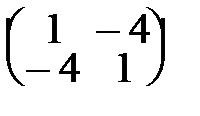 . . |
Задание 6. Дан треугольник с вершинами A(x 1, y 1), B(x 2, y 2), C(x 3, y 3). Найти:
(а) уравнение стороны АС;
(б) уравнение высоты АК;
(в) длину средней линии MP/BC;
(г) угол 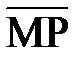 ^
^ 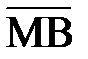 ;
;
(д) точку пересечения высот треугольника.
51. А (-4,0), B (-2,6), C (2,2).
52. A (-3,0), B (-1,6), C (3,2).
53. A (-2,0), B (0,6), C (4,2).
54. A (-1,0), B (1,6), C (5,2).
55. A (0,0), B (2,6), C (6,2).
56. A (1,0), B (3,6), C (7,2).
57. A (2,0), B (4,6), C (8,2).
58. A (3,0), B (5,6), C (9,2).
59. A (4,0), B (6,6), C (10,2).
60. A (-5,0), B (-1,6), C (1,2).
Задание 7. Найти:
а) уравнение прямой 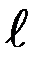 , проходящей через точки А(x 1, y 1, z 1); B(x 2, y 2, z 2).
, проходящей через точки А(x 1, y 1, z 1); B(x 2, y 2, z 2).
б) уравнение плоскости 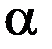 , проходящей через точки 0(0, 0, 0), С(0, y 3, 1) параллельно прямой
, проходящей через точки 0(0, 0, 0), С(0, y 3, 1) параллельно прямой 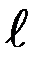 .
.
в) пересечение прямой с плоскостью H: с x +a y + z +1=0.
61. A(1,2,3), B(3,4,4), C(0,-3,1), H: 3 x + y +2 z +1=0.
62. A(1,1,2), B(3,2,3), C(0,-4,1), H: 2 x + y + z +1=0.
63. A(1,1,1), B(3,3,2), C(0,-4,1), H: x + y + z +1=0.
64. A(1,1,3), B(3,2,4), C(0,-4,1), H: 3 x + y + z +1=0.
65. A(2,1,1), B(5,2,2), C(0,-4,1), H: x +2 y + z +1=0.
66. A(2,2,1), B(5,4,2), C(0,-3,1), H: x +2 y +2 z +1=0.
67. A(3,2,1), B(7,4,2), C(0,-3,1), H: x +3 y +2 z +1=0.
68. A(3,2,2), B(7,4,2), C(0,-3,1), H: 2 x +3 y +2 z +1=0.
69. A(4,1,1), B(9,2,2), C(0,-4,1), H: x +4 y + z +1=0.
70. A(4,2,1), B(9,4,2), C(0,-3,1), H: x +4 y +2 z +1=0.
Задание 8. Решить графическим методом задачу линейной оптимизации
81. 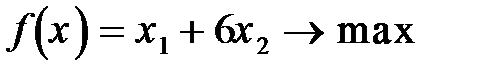 82.
82. 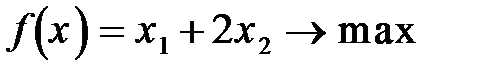
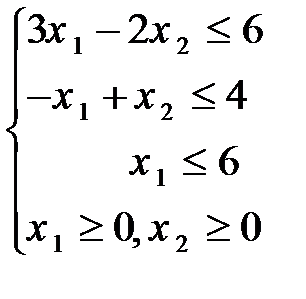
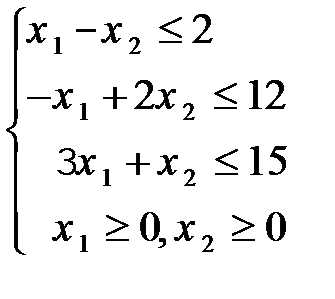
83. 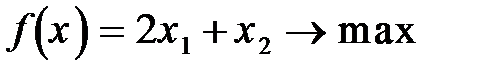 84.
84. 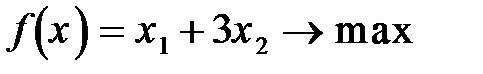
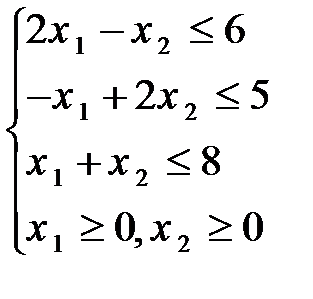
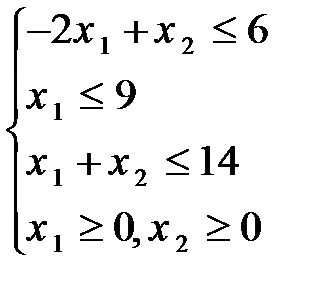
85. 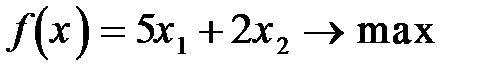 86.
86. 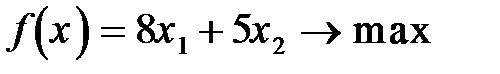
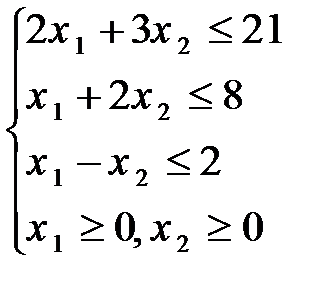
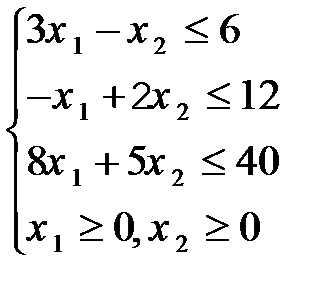
87. 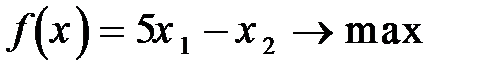 88.
88. 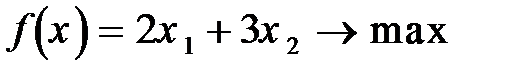
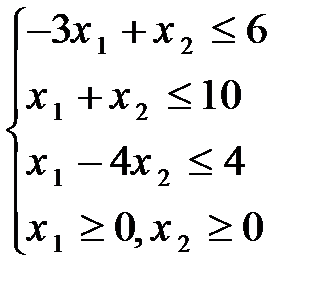
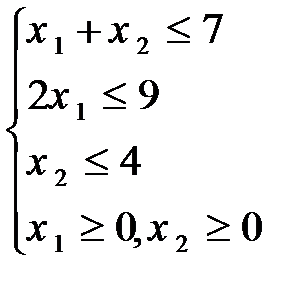
89. 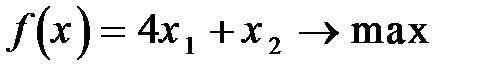 90.
90. 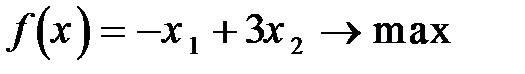
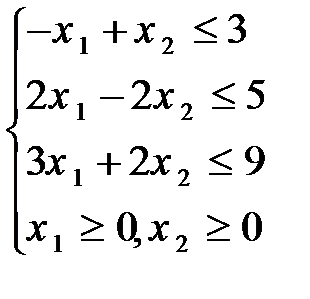
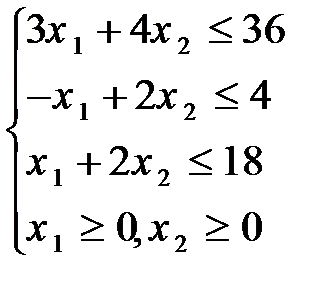
Задание 9. Решить симплексным методом задачу линейной оптимизации:
. 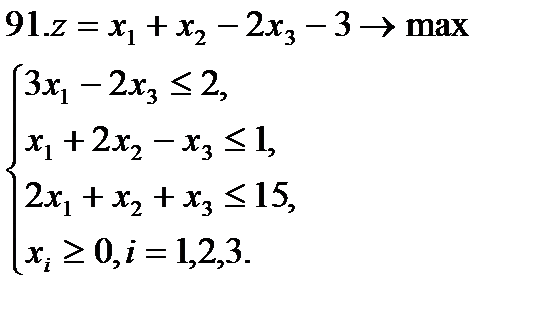
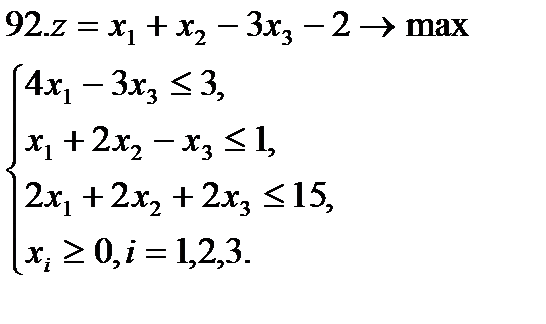
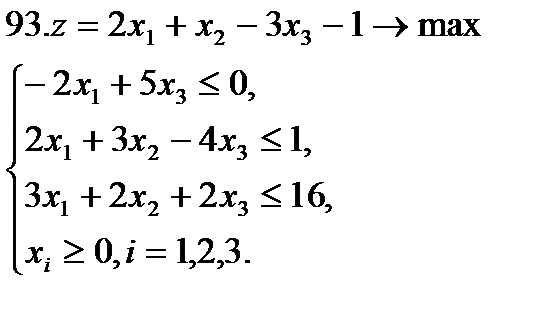
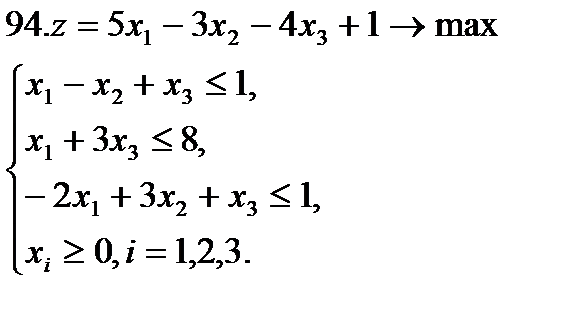
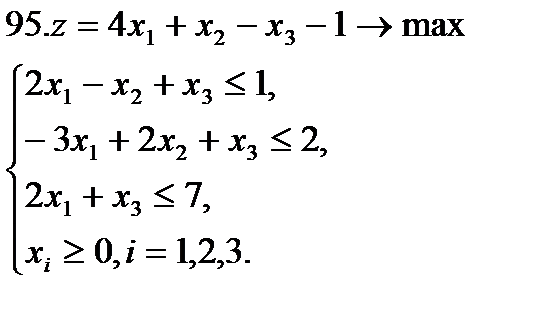
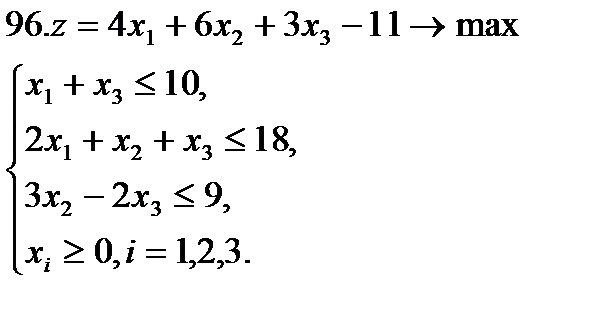
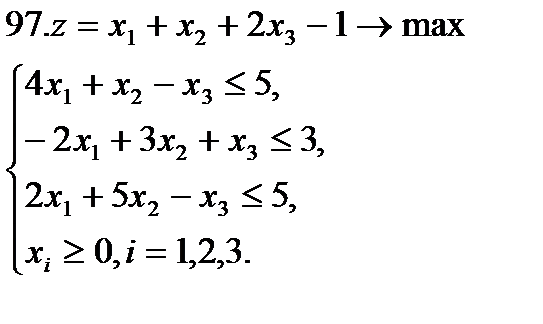
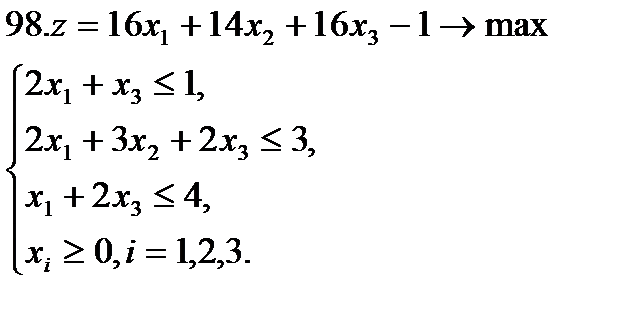
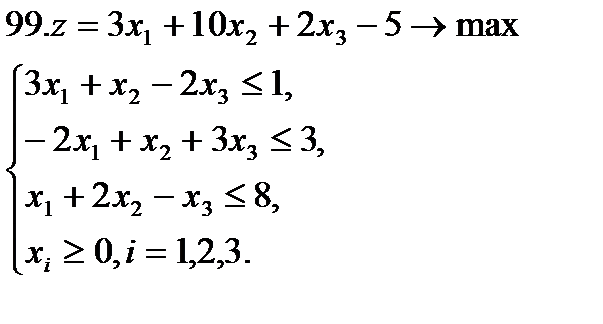
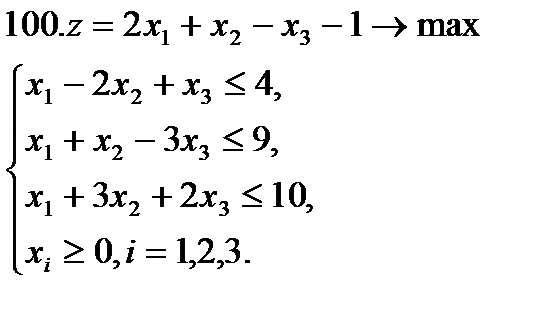
Задание 10. Решить транспортную задачу (в верхней строке таблицы указаны потребности bj в грузе пунктов назначения, в левом столбце – запасы ai груза в пунктах отправления, в остальных клетках – тарифы cij):
| ai/bj | ||||
101. 102.
| ai/bj | ||||
103. 104.
| ai/bj | ||||
| ai/bj | ||||
105. 106.
| ai/bj | ||||
| ai/bj | ||||
| ai/bj | ||||
| ai/bj | ||||
107. 108.
109. 110.
| ai/bj | ||||
| ai/bj | ||||
Методические указания по курсу линейной алгебры
В методических указаниях даны примеры решения задач, поясняющих применение основных теоретических результатов и некоторых приложений линейной алгебры. Задачи охватывают основные вопросы линейной алгебры: системы линейных уравнений, матрицы, линейное пространство, линейные операторы и квадратичные формы, линейное программирование. По ходу решения приведены некоторые теоретические понятия, знание которых необходимо для решения задач.
 2015-03-22
2015-03-22 1658
1658
