Аналитическая геометрия дает нам наглядное представление различных понятий и теорем линейной алгебры.
Определение. Гиперплоскостью в 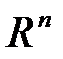 называется множество решений линейного уравнения
называется множество решений линейного уравнения
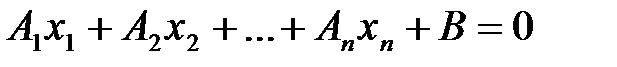 , (1)
, (1)
где хотя бы один из коэффициентов 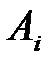 отличен от нуля. Уравнение (1) называют общим уравнением гиперплоскости.
отличен от нуля. Уравнение (1) называют общим уравнением гиперплоскости.
Замечание. Гиперплоскость в 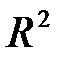 :
: 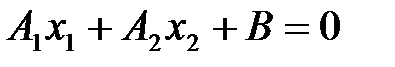 – прямая, гиперплоскость в
– прямая, гиперплоскость в 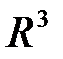 :
: 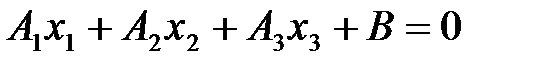 – обычная плоскость.
– обычная плоскость.
Выясним геометрический смысл коэффициентов 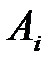 . Фиксируем на гиперплоскости Р точку
. Фиксируем на гиперплоскости Р точку 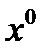 . Ее координаты обращают (1) в тождество
. Ее координаты обращают (1) в тождество
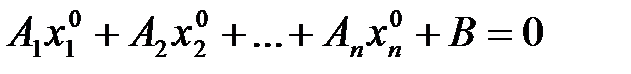 . (2)
. (2)
Вычтем (2) из (1), получим
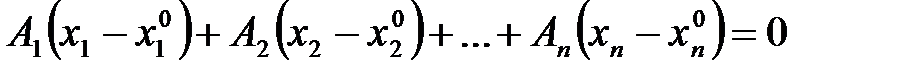 (3)
(3)
или
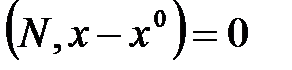 . (3/)
. (3/)
Из (3/) следует, что вектор 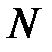 ортогонален любому вектору
ортогонален любому вектору  , где
, где 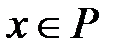 , т.е. ортогонален гиперплоскости.
, т.е. ортогонален гиперплоскости.
Вектор 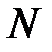 называется вектором нормали гиперплоскости
называется вектором нормали гиперплоскости 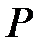 . Уравнение (3) называют уравнением гиперплоскости, проходящей через данную точку.
. Уравнение (3) называют уравнением гиперплоскости, проходящей через данную точку.
Определение. Углом 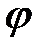 между двумя гиперплоскостями с векторами нормали
между двумя гиперплоскостями с векторами нормали 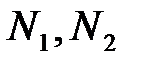 называется угол, определенный формулой
называется угол, определенный формулой
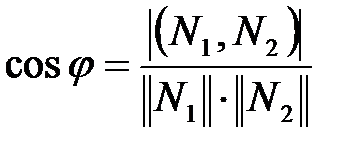 . (4)
. (4)
Гиперплоскости называются параллельными, если и только если 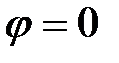 и ортогональными, если и только если
и ортогональными, если и только если 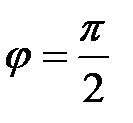 .
.
Следовательно, если 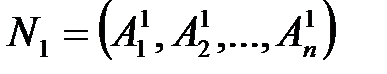 ,
, 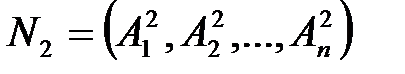 , то
, то
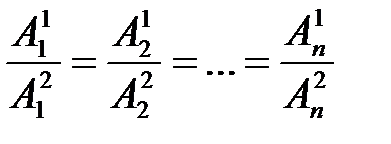 – условие параллельности гиперплоскостей
– условие параллельности гиперплоскостей
(в случае ненулевых  );
);
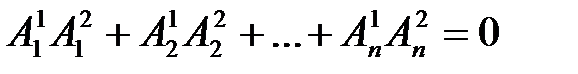 – условие ортогональности.
– условие ортогональности.
Задача 8. Найти уравнение гиперплоскости:
1) проходящей через точку 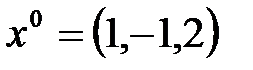 параллельно гиперплоскости
параллельно гиперплоскости 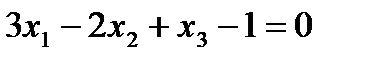 ;
;
2) проходящей через точки 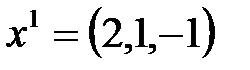 ,
, 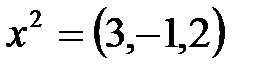 ортогонально гиперплоскости
ортогонально гиперплоскости 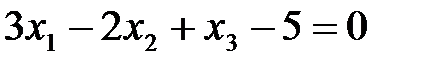 .
.
Решение. 1) Воспользуемся уравнением гиперплоскости, проходящей через данную точку в 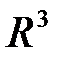 :
:
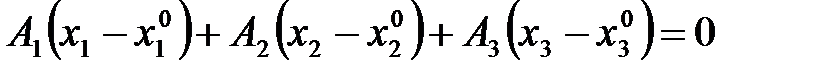 .
.
Координаты точки 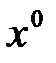 нам даны, а из условия параллельности следует, что в качестве вектора нормали можно взять вектор вида
нам даны, а из условия параллельности следует, что в качестве вектора нормали можно взять вектор вида 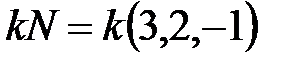 , где
, где 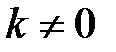 . Подставляя в уравнение, получим:
. Подставляя в уравнение, получим:
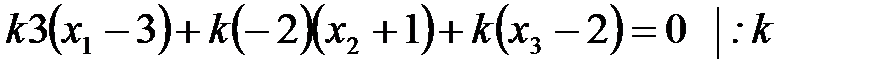 ,
,
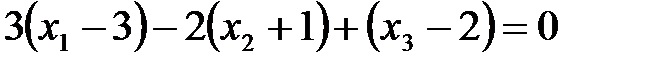
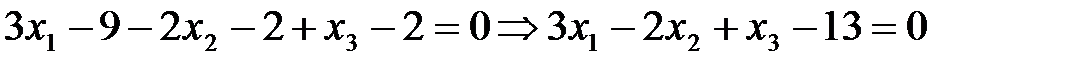 .
.
Ответ: 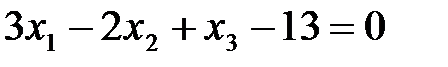 .
.
2) Пусть 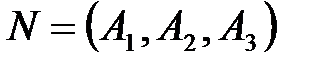 – вектор нормали искомой плоскости. Тогда уравнение плоскости, проходящей через точку
– вектор нормали искомой плоскости. Тогда уравнение плоскости, проходящей через точку 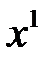 , имеет вид:
, имеет вид:
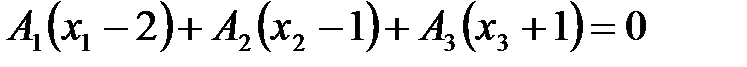 .
.
Так как точка 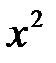 принадлежит этой плоскости, то ее координаты удовлетворяют уравнению этой плоскости:
принадлежит этой плоскости, то ее координаты удовлетворяют уравнению этой плоскости:
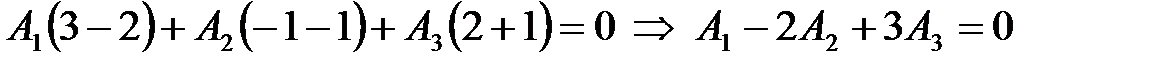 .
.
Воспользуемся также условием перпендикулярности искомой и данной плоскостей с вектором нормали 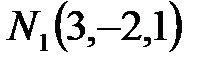 :
:
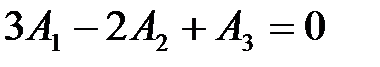 .
.
Мы получим для определения 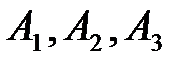 систему двух уравнений:
систему двух уравнений:
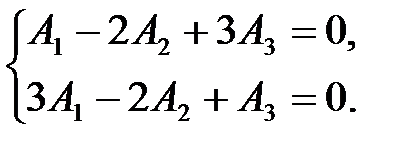
Решим ее методом Жордана-Гаусса:
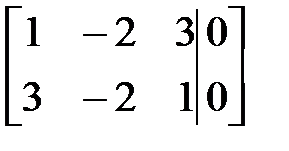 ~
~ 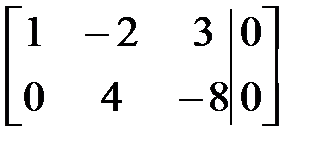 ~
~ 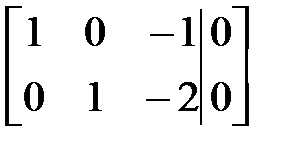
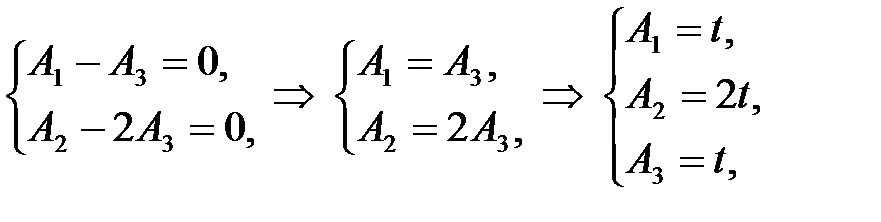 где
где 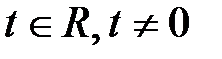 .
.
Подставим в первое уравнение:
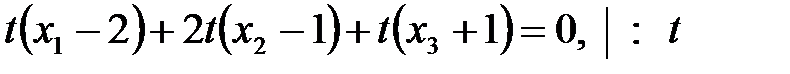
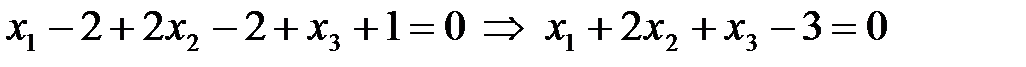
Ответ: 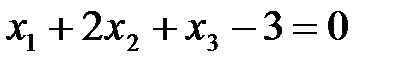 .
.
Определение. Прямой в 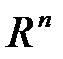 называется множество точек вида
называется множество точек вида
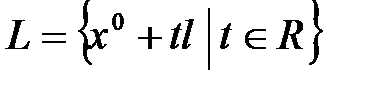 , (5)
, (5)
где 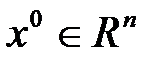 – фиксированная точка,
– фиксированная точка, 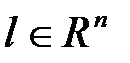 – фиксированный ненулевой вектор.
– фиксированный ненулевой вектор.
Вектор  называется направляющим вектором прямой
называется направляющим вектором прямой 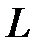
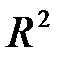 :
: 
 ·
· 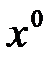 или ·
или · 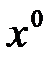
Уравнение 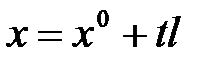 , которому при
, которому при 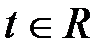 удовлетворяют все точки прямой
удовлетворяют все точки прямой 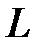 , называется параметрическим (векторным) уравнением прямой
, называется параметрическим (векторным) уравнением прямой 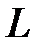 . Если мы распишем его в координатном виде, то получим систему:
. Если мы распишем его в координатном виде, то получим систему:
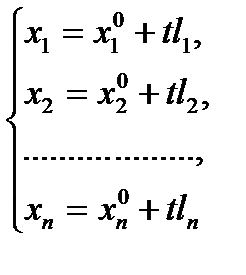 , (6)
, (6)
которую называют параметрическими уравнениями прямой.
Замечание. Параметрическое уравнение однозначно определяет прямую, но не наоборот, т.к. если мы возьмем любой ненулевой вектор 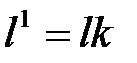 (
(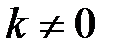 ) и другую точку
) и другую точку 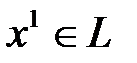 , то уравнение
, то уравнение 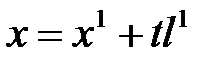 будет также задавать прямую
будет также задавать прямую 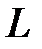 .
.
Если все 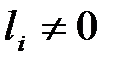 , то разрешив (6) относительно
, то разрешив (6) относительно 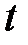 , мы получим цепочку из
, мы получим цепочку из 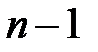 равенств:
равенств:
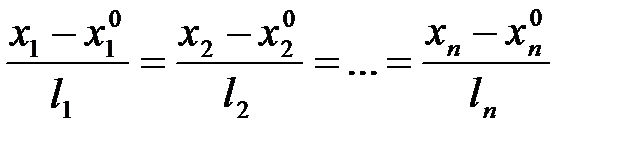 , (7)
, (7)
она называется каноническим уравнением прямой.
Замечание. Каноническое уравнение – это сокращенная запись системы 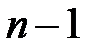 уравнений, а не одно уравнение.
уравнений, а не одно уравнение.
Замечание. Если некоторые из чисел 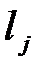 равны нулю, то соответствующие параметрические уравнения принимают вид:
равны нулю, то соответствующие параметрические уравнения принимают вид: 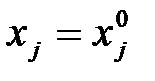 , ему удовлетворяют любые
, ему удовлетворяют любые 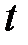 , поэтому цепочка (7) укорачивается и к ней добавляются равенства
, поэтому цепочка (7) укорачивается и к ней добавляются равенства 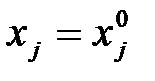 . Например, при
. Например, при 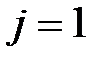 :
:
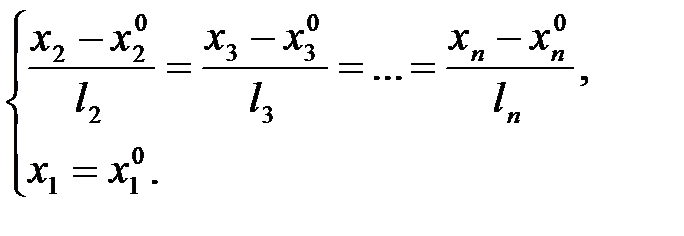
Теорема (общие уравнения прямой). Множество решений системы 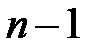 линейных уравнений с
линейных уравнений с 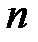 неизвестными:
неизвестными:
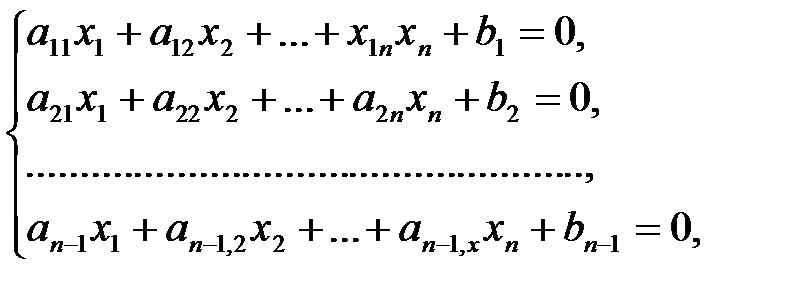 (8)
(8)
является прямой в 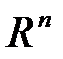 , если и только если ранг матрицы системы равен
, если и только если ранг матрицы системы равен 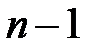 (т.е. максимален).
(т.е. максимален).
Определение. Если прямая 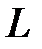 – множество решений системы (8), то эту систему называют общими уравнениями прямой.
– множество решений системы (8), то эту систему называют общими уравнениями прямой.
Геометрическое истолкование: прямая в 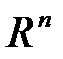 является пересечением
является пересечением 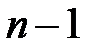 гиперплоскостей. Следовательно, прямая в
гиперплоскостей. Следовательно, прямая в 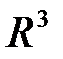 – это пересечение двух плоскостей, если они не параллельны или не совпадают.
– это пересечение двух плоскостей, если они не параллельны или не совпадают.
Задача 9. Выяснить, определяет ли системы уравнений прямую в 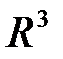 и, если определяет, то найти параметрические уравнения прямой:
и, если определяет, то найти параметрические уравнения прямой:
а) 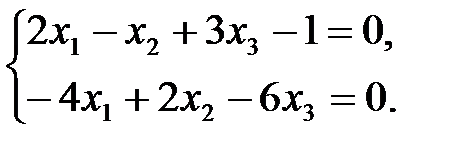 б)
б) 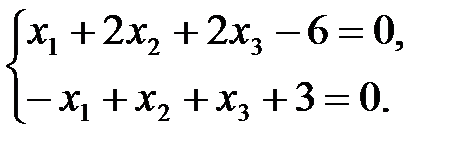
Решение. а) Найдем 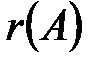 , где
, где
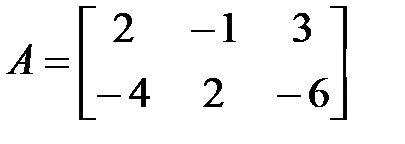 ~
~ 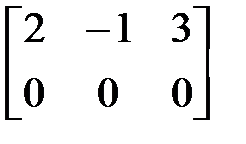
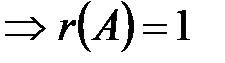 .
.
Т.к. 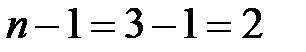 , то система не определяет прямую.
, то система не определяет прямую.
б) 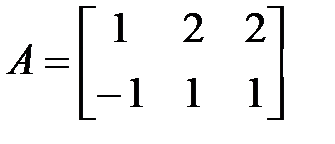 ~
~ 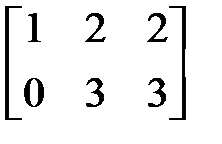
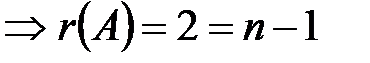 ,
,
т.е. система определяет прямую. Найдем общее решение системы по методу Жордана-Гаусса:
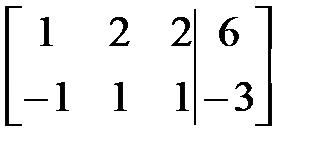 ~
~ 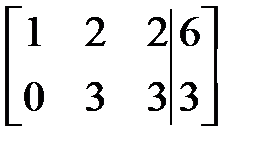 ~
~ 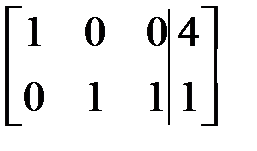
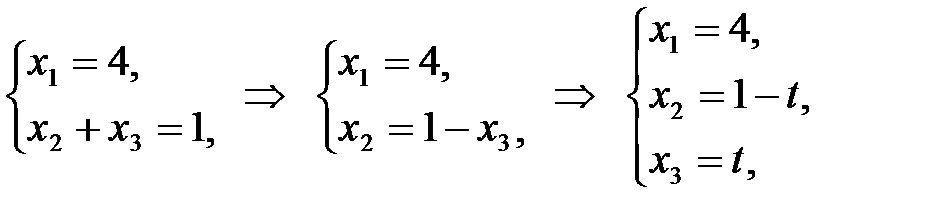 где
где 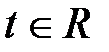 .
.
Параметрическое уравнение прямой: 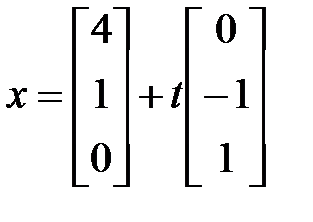 ,
, 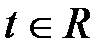 .
.
Если все координаты точек 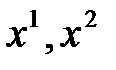 различны, то цепочка равенств
различны, то цепочка равенств
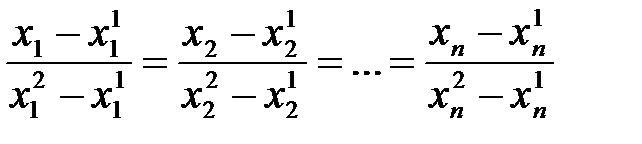 . (9)
. (9)
называется уравнением прямой, проходящей через две точки.
Если какая-то пара соответствующих координат точек 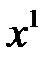 и
и 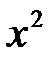 равна, то цепочка уравнений укорачивается (см. замечание к уравнению (7).
равна, то цепочка уравнений укорачивается (см. замечание к уравнению (7).
 2015-03-22
2015-03-22 1490
1490








