Определение. Система векторов 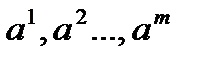 векторного пространства
векторного пространства 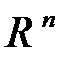 называются линейно зависимой, если существуют числа
называются линейно зависимой, если существуют числа 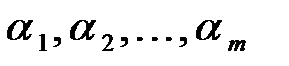 , не равные одновременно нулю и такие, что
, не равные одновременно нулю и такие, что
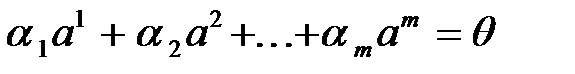 . (1)
. (1)
(справа стоит нулевой вектор).
Векторы, не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами, векторы 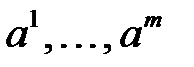 линейно независимы, если равенство (1) справедливо только при
линейно независимы, если равенство (1) справедливо только при
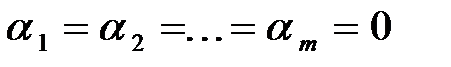 .
.
Задача 5. Выяснить является ли система векторов линейно зависимой или линейно независимой, в случае линейной зависимости привести пример нетривиальной линейной комбинации, равной нулевому вектору (представить один из векторов в виде линейной комбинации остальных).
1) Дана система векторов: 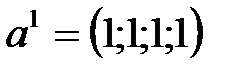 ,
, 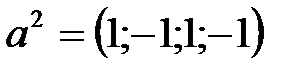 ,
, 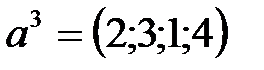 .
.
Решение. Составим линейную комбинацию векторов с коэффициентами 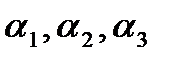 , равную
, равную 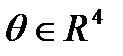 :
:
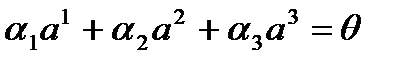 . (1)
. (1)
От векторной формы перейдем к координатной:
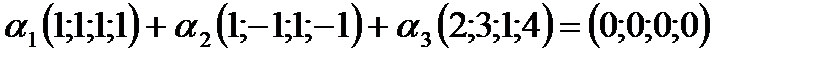 .
.
Отсюда, выполнив в левой части преобразования по правилам действий над векторами, на основании равенства векторов получим:
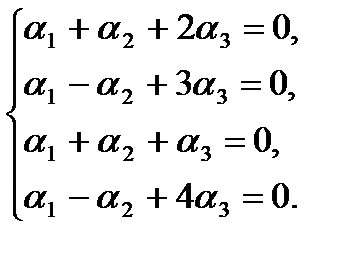
Решая систему уравнений одним из рассмотренных выше методов, найдем, что она имеет только тривиальное решение:
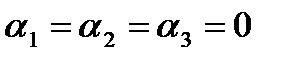 .
.
Мы получили, что линейная комбинация может быть нулевой только, если все ее коэффициенты равны нулю. По определению линейной независимости система векторов 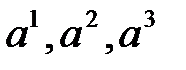 линейно независима.
линейно независима.
2) Дана система векторов:
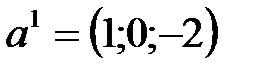 ,
, 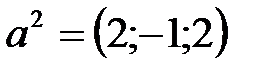 ,
, 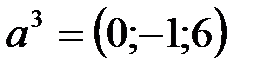 .
.
Решение. Проведя рассуждения и преобразования аналогично предыдущим, получим систему уравнений:
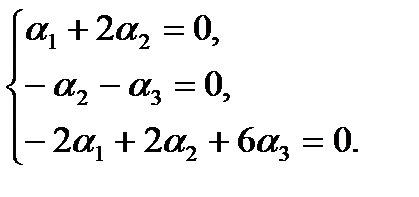
Преобразуем систему, используя алгоритм метода Жордана-Гаусса или жордановых исключений. Сделав два шага, придем к виду:
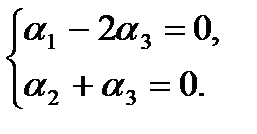 или
или 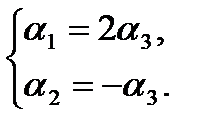
Система приведена к единичному базису, переменные 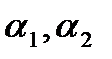 - базисные,
- базисные, 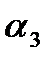 - свободная переменная. В данном случае
- свободная переменная. В данном случае 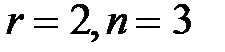 ,
, 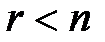 , следовательно, система неопределенная. Общее решение системы
, следовательно, система неопределенная. Общее решение системы 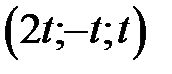 , где
, где 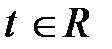 , т.е. система имеет не только нулевое решение (тривиальное), и по определению система векторов
, т.е. система имеет не только нулевое решение (тривиальное), и по определению система векторов 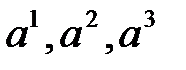 линейно зависима.
линейно зависима.
Приведем пример нетривиальной линейной комбинации, равной 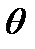 . Для этого найдем одно из частных нетривиальных решений системы, например, положим в решении системы
. Для этого найдем одно из частных нетривиальных решений системы, например, положим в решении системы 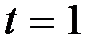 , получим частное решение
, получим частное решение 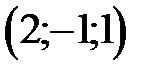 и подставим его в равенство (1):
и подставим его в равенство (1):
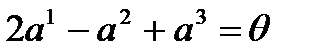 или
или 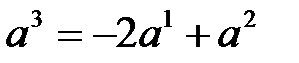 , т.е.
, т.е.
вектор 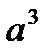 представлен в виде линейной комбинации векторов
представлен в виде линейной комбинации векторов 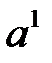 и
и 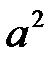 .
.
Задача 6. Показать, что векторы 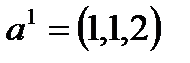 ,
, 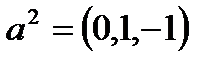 ,
, 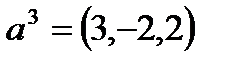 образуют в
образуют в 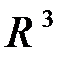 базис и разложить вектор
базис и разложить вектор 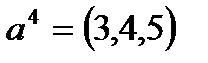 по этому базису.
по этому базису.
Решение. Исходя из определения базиса 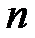 -мерного пространства надо показать, что 1) число векторов совпадает с размерностью пространства; 2) эти векторы линейно независимы.
-мерного пространства надо показать, что 1) число векторов совпадает с размерностью пространства; 2) эти векторы линейно независимы.
Первое очевидно. В том, что система векторов 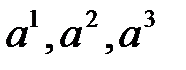 линейно независима, можно убедиться, посчитав определитель, составленный из координат векторов, и убедиться, что он отличен от нуля.
линейно независима, можно убедиться, посчитав определитель, составленный из координат векторов, и убедиться, что он отличен от нуля.
Итак, векторы 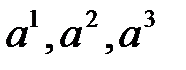 образуют базис в
образуют базис в 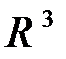 . Следовательно, можно записать:
. Следовательно, можно записать:
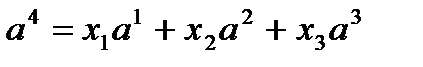 .
.
Перейдем от векторной формы записи к координатной:
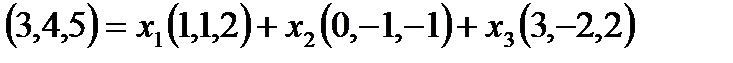 .
.
Отсюда, проведя преобразования в правой части по правилам действий над векторами, получим, учитывая равенство векторов:
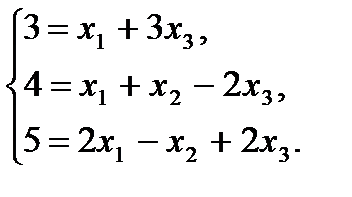
Решая систему линейных уравнений с переменными 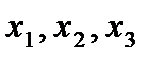 , найдем, что она имеет единственное решение:
, найдем, что она имеет единственное решение:
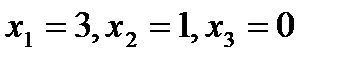 .
.
Следовательно, искомое разложение вектора 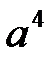 по базису
по базису 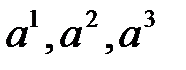 имеет вид:
имеет вид: 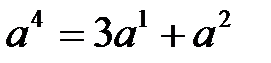 , или в базисе системы векторов
, или в базисе системы векторов 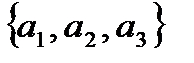 вектор
вектор 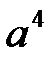 имеет координаты (3,1,0).
имеет координаты (3,1,0).
 2015-03-22
2015-03-22 921
921








