Постановка ТЗ

ТЗ возникает при планировании рациональных перевозок грузов.

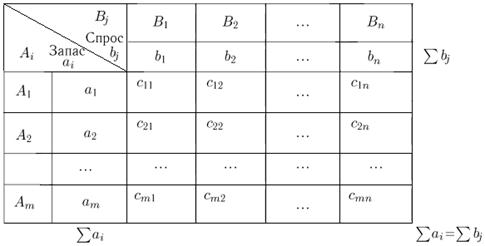
Имеются m пунктов отправления однородного груза А ₁, А ₂,..., А_m (поставщики) и n пунктов назначения того же груза В ₁, В ₂,..., В_n (потребители). Предполагается, что из любого пункта A_i (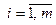) груз может быть доставлен в любой пункт В_j (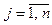). Известны объемы (запасы) груза поставщиков (a_i > 0), потребности в грузе (спрос) потребителей (b_j > 0), стоимость (тариф) перевозки единицы груза из каждого пункта отправления в любой пункт назначения (c_ij ≥ 0).

Требуется определить оптимальный план перевозок груза из пунктов A_i в пункты В_j так, чтобы: 1) вывезти весь груз от отправителей A_i; 2) удовлетворить потребность в грузе (спрос) каждого потребителя В_j; 3) транспортные расходы были минимальными.

Допустимый план перевозок – решение задачи в виде неотрицательной матрицы

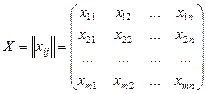где x_ij – количество груза, перевозимого из точки A_i (от i -го поставщика) в точку В_j (к j -му потребителю).

Математическая модель ТЗ:

Матрица X должна удовлетворять условиям ограничений:

, ,

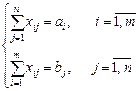
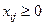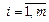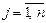
и доставлять минимум целевой функции (транспортных расходов) .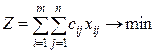

Допустимый план, имеющий не более (m + n -1) отличных от нуля компонентов x_ij, называется базисным (опорным) планом.

Опорный план называется оптимальным, если он доставляет минимум целевой функции.

Ранг матрицы системы – это число 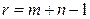(количество строк плюс количество столбцов и минус единица).

Если число заполненных клеток в таблице равно рангу матрицы, то опорный план называется невырожденным, иначе – вырожденным. Невырожденный опорный план имеет ровно (m + n -1) отличных от нуля компонент. Вырожденный опорный план имеет меньше, чем (m + n -1) число отличных от нуля компонент.

Любая ТЗ имеет опорный план, если выполняется условие баланса 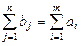. В этом случае модель ТЗ называется закрытой. Если модель ТЗ не удовлетворяет условию баланса, тогда она называется открытой.

Если задача открытая то:

1) при 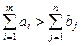(спрос меньше предложения) вводят «фиктивного» потребителя 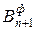с потребностью 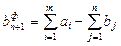. Стоимости перевозок от любого поставщика до «фиктивного» потребителя принимаются равными нулю: c_i _, _n ₊₁=0 ();

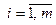2) при 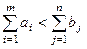(спрос больше предложения) вводят «фиктивного» поставщика 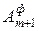с запасом 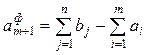. Стоимости перевозок от «фиктивного» поставщика до всех потребителей принимаются равными нулю: c_m _+1, _j =0 ().

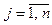ТЗ представляют в виде распределительной таблицы. Тарифы c_ij будем записывать в левом верхнем углу клетки, а величины поставок x_ij – в правом нижнем углу клетки.

Модель ТЗ относится к ЗЛП и может быть решена симплексным методом. Однако для ее решения созданы специальные алгоритмы. Самый распространенный метод решения – метод потенциалов.

Решение ТЗ включает два этапа: 1) определение начального опорного плана – первоначальное распределение поставок груза; 2) выполнение последовательности шагов, улучшающих опорные планы (каждый новый план не должен увеличивать суммарные затраты) до тех пор, пока не будет найден оптимальный план.

5.2 Построение начального опорного плана

План составляется последовательным заполнением по одной клетке в таблице перевозок так, что на каждом шаге заполнения либо полностью удовлетворяется потребность одного из потребителей, либо полностью вывозится груз от одного поставщика.

В теории доказывается, что если система ограничений состоит из m + n уравнений с количеством mn переменных, то ее базисное решение в условиях транспортной задачи имеет m + n -1 базисных переменных (ранг системы m + n -1). Поэтому, совершив m + n -1 шагов заполнения клеток таблицы, получим 1-й опорный план.

Заполненные перевозками клетки называются базисными, а остальные (пустые) – свободными.

Рассмотрим два метода построения 1-го (начального) опорного плана, которые различаются по способу выбора последовательности заполнения клеток.