Симплексный метод − это метод упорядоченного перебора опорных планов (упорядоченность обеспечивается монотонным изменением значения целевой функции при переходе к очередному плану). При этом необходимо соблюдать принцип: каждый следующий шаг должен улучшить или, в крайнем случае, не ухудшить значение целевой функции.
Для решения ЗЛП симплекс-методом ее приводят к каноническому виду, т.е. из ограничений – неравенств надо сделать ограничения – равенства. Для этого в каждое ограничение вводится дополнительная неотрицательная балансовая переменная со знаком «+», если знак неравенства «£», и со знаком «–», ели знак неравенства «³».
В целевой функции эти дополнительные переменные входят с нулевыми коэффициентами, т.е. запись целевой функции не изменится. Каждую переменную, на которую не наложено условие неотрицательности, можно представить в виде разности двух неотрицательных переменных: 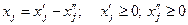 .
.
Если ограничения задачи отображают наличие и расход ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в канонической форме, равно объему неиспользованного ресурса.
Для решения задачи симплекс-методом будем использовать укороченные симплексные таблицы системы линейных уравнений и метод модифицированного жорданова исключения.
1. Составляем первый опорный план
Задача остается прежней. Приведем стандартную форму системы неравенств (1) в каноническую форму системы уравнений путем введения дополнительных балансовых переменных x 3, x 4, x 5, x 6.
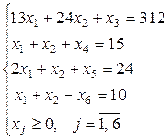 или
или 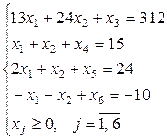
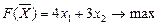 .
.
В экономическом смысле значения дополнительных переменных x 3, x 4, x 5 определяют остатки сырья после реализации продукции.
Матрица полученной системы уравнений 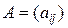 имеет вид:
имеет вид:
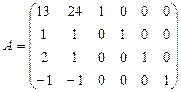
Видно, что в матрице A базисным минором 4-го порядка является определитель, составленный из единичных коэффициентов при дополнительных переменных x 3, x 4, x 5, x 6, так как он отличен от нуля и равен 1. Это означает, что векторы-столбцы при этих переменных является линейно независимыми, т.е. образуют базис, а соответствующие им переменные x 3, x 4, x 5, x 6 являются базисными (основными). Переменные x 1, x 2 будут называться свободными (неосновными).
Если свободным переменным x 1 и x 2 задавать различные значения, то, решая систему относительно базисных переменных, получим бесконечное множество частных решений. Если свободным переменным задавать только нулевые значения, то из бесконечного множества частных решений выделяют базисные решения – опорные планы.
Чтобы выяснить, могут ли переменные быть базисными, необходимо вычислить определитель, состоящий из коэффициентов при этих переменных. Если данный определитель не равен нулю, то эти переменные могут быть базисными.
Количество базисных решений и соответствующее ему число групп базисных переменных может быть не более, чем 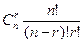 , где n –общее число переменных, r – число базисных переменных, r ≤ m ≤ n.
, где n –общее число переменных, r – число базисных переменных, r ≤ m ≤ n.
Для нашей задачи r = 4; n = 6. Тогда 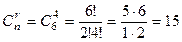 , т.е. возможны 15 групп из 4-х базисных переменных (или 15 базисных решений).
, т.е. возможны 15 групп из 4-х базисных переменных (или 15 базисных решений).
Разрешим систему уравнений относительно базисных переменных x 3, x 4, x 5, x 6:
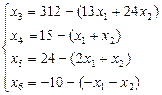
Полагая, что свободные переменные x 1 = 0, x 2 = 0, получим значения базисных переменных: x 3 = 312; x 4 = 15; x 5 = 24; x 6 = –10, т.е. базисное решение будет 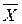 = (0; 0; 312; 15; 24; –10).
= (0; 0; 312; 15; 24; –10).
Данное базисное решение является недопустимым, т.к. x 6 = –10 ≤ 0, а по условию ограничений x 6 ≥ 0. Поэтому вместо переменной x 6 в качестве базисной надо взять другую переменную из числа свободных x 1 или x 2.
Дальнейшее решение будем выполнять, используя укороченные симплексные таблицы, заполнив строки первой таблицы коэффициентами системы следующим образом (табл. 1):
Таблица 1
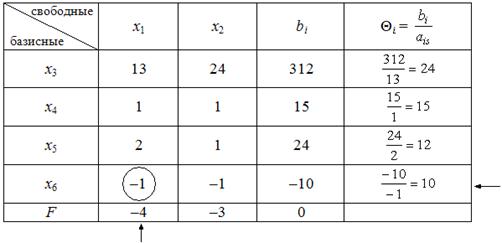
F –строка называется индексной. Она заполняется коэффициентами целевой функции, взятыми с противоположными знаками, так как уравнение функции 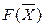 можно представить в виде F = 0 – (– 4 x 1 – 3 x 2).
можно представить в виде F = 0 – (– 4 x 1 – 3 x 2).
В столбце свободных членов bi есть отрицательный элемент b 4 = –10, т.е. решение системы является недопустимым. Чтобы получить допустимое решение (опорный план), элемент b 4 надо сделать неотрицательным.
Выбираем x 6-строку с отрицательным свободным членом. В этой строке есть отрицательные элементы. Выбираем любой из них, например, «–1» в x 1-столбце, и x 1-столбец принимаем в качестве разрешающего столбца (он определит, что переменная x 1 перейдет из свободных в базисные).
Делим свободные члены bi на соответствующие элементы ais разрешающего столбца, получаем оценочные отношения Θ i = 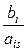 = {24, 15, 12, 10}. Из них выбираем наименьшее положительное (minΘ i =10), которое будет соответствовать разрешающей строке. Разрешающая строка определяет переменную xj, которая на следующем шаге выступает из базиса и станет свободной. Поэтому x 6-строка является разрешающей строкой, а элемент «–1» – разрешающим элементом. Обводим его кружком. Переменные x 1 и x 6 меняются местами.
= {24, 15, 12, 10}. Из них выбираем наименьшее положительное (minΘ i =10), которое будет соответствовать разрешающей строке. Разрешающая строка определяет переменную xj, которая на следующем шаге выступает из базиса и станет свободной. Поэтому x 6-строка является разрешающей строкой, а элемент «–1» – разрешающим элементом. Обводим его кружком. Переменные x 1 и x 6 меняются местами.
Оценочные отношения Θ i в каждой строке определяются по правилам:
1) Θ i = 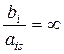 , если bi и ais имеют разные знаки;
, если bi и ais имеют разные знаки;
2) Θ i = ∞, если bi = 0 и ais < 0;
3) Θ i = ∞, если ais = 0;
4) Θ i = 0, если bi = 0 и ais > 0;
5) Θ i = 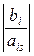 , если bi и ais имеют одинаковые знаки.
, если bi и ais имеют одинаковые знаки.
Совершаем шаг модифицированного жорданова исключения (ШМЖИ) с разрешающим элементом и составляем новую таблицу (табл. 2) по следующему правилу:
1) на месте разрешающего элемента (РЭ) устанавливается величина, ему обратная, т.е. 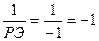 ;
;
2) элементы разрешающей строки делятся на РЭ;
3) элементы разрешающего столбца делятся на РЭ и знак меняется;
4) остальные элементы находятся по правилу прямоугольника:
 .
.
Из табл. 2 видно, что свободные члены в bi -столбце являются неотрицательными, следовательно, получено первоначальное допустимое решение – первый опорный план 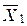 = (10; 0; 182; 5; 4; 0). При этом значение функции F (
= (10; 0; 182; 5; 4; 0). При этом значение функции F (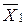 ) = 40. Геометрически это соответствует вершине F (10; 0) многоугольника решений (рис. 1).
) = 40. Геометрически это соответствует вершине F (10; 0) многоугольника решений (рис. 1).
Таблица 2
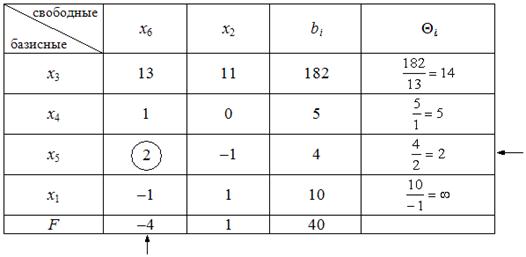
2. Проверяем план на оптимальность. Опорный план 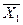 не оптимальный, так как в F -строке имеется отрицательный коэффициент «–4». Улучшаем план.
не оптимальный, так как в F -строке имеется отрицательный коэффициент «–4». Улучшаем план.
3. Нахождение нового опорного плана
Выбираем разрешающий элемент по правилу:
- выбираем наименьший отрицательный коэффициент в F -строке «–4», который и определяет разрешающий столбец – x 6; переменную x 6 переводим в базисные;
- находим отношения Θ i, среди них выбираем наименьшее положительное, которое соответствует разрешающей строке:
min Θ i = min {14, 5, 2, ∞} = 2, следовательно, x 5-строка – разрешающая, переменную x 5 переводим в свободные (переменные x 5 и x 6 меняются местами).
- на пересечении разрешающих строки и столбца стоит разрешающий элемент «2»;
- выполняем шаг ШМЖИ, строим табл. 3 по вышеприведенному правилу и получаем новый опорный план 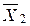 = (12; 0; 156; 3; 0; 2).
= (12; 0; 156; 3; 0; 2).
Таблица 3
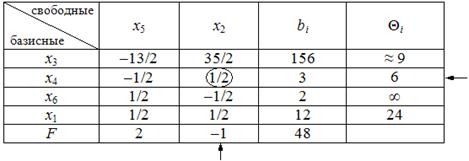
4. Проверка нового опорного плана на оптимальность
Опорный план 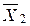 также не является оптимальным, так как в F -строке имеется отрицательный коэффициент «–1». Значение функции F (
также не является оптимальным, так как в F -строке имеется отрицательный коэффициент «–1». Значение функции F (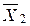 ) = 48, что геометрически соответствует вершине E (12; 0) многоугольника решений (рис. 1). Улучшаем план.
) = 48, что геометрически соответствует вершине E (12; 0) многоугольника решений (рис. 1). Улучшаем план.
5. Нахождение нового опорного плана
x 2-столбец – разрешающий, так как в F -строке наименьший отрицательный коэффициент «–1» находится в x 2-столбце (Δ2 = –1). Находим наименьшее Θ i: min Θ i = min {≈ 9, 6, ∞, 24} = 6, следовательно, x 4-строка – разрешающая. Разрешающий элемент «1/2». Меняем местами переменные x 2 и x 4. Выполняем шаг ШМЖИ, строим табл. 4, получаем новый опорный план 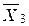 = (9; 6; 51; 0; 0; 5).
= (9; 6; 51; 0; 0; 5).
6. Проверка опорного плана на оптимальность
В F -строке все коэффициенты неотрицательны, следовательно, опорный план 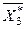 является оптимальным. Геометрически
является оптимальным. Геометрически 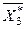 соответствует точке D (9;6) (см. рис. 1). Оптимальный план
соответствует точке D (9;6) (см. рис. 1). Оптимальный план 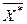 дает максимальное значение целевой функции
дает максимальное значение целевой функции 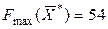 у.е.
у.е.
Таблица 4
| свободные базисные | x 5 | x 4 | bi |
| x 3 | –35 | ||
| x 2 | –1 | ||
| x 6 | |||
| x 1 | –1 | ||
| F |
Таким образом, необходимо производить 9 единиц продукции I вида (x *1 = 9) и 6 единиц продукции II вида (x *2 = 6). Значения коэффициентов F -строки – ненулевые, поэтому полученный оптимальный план является единственным. F -строка позволяет представить целевую функцию через свободные переменные x 4 и x 5: 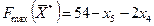 .
.
В оптимальном плане фигурируют значения дополнительных переменных x 3 = 31; x 6 = 5. Это означает, что сырье вида С недоиспользовано на 51 кг, а сырье видов А и В (x 4 = 0; x 5 = 0) израсходовано полностью и является дефицитным. Значение дополнительной переменной x 6 = 5 означает превышение общего количества произведенной продукции над ограничением: x 1 + x 2 ≥ 10.
Замечания:
1) Если в индексной F -строке будет находиться нуль, принадлежащий свободной переменной, а в соответствующем столбце (содержащем этот нуль) имеется хотя бы один положительный элемент, то задача имеет множество оптимальных планов. Эту свободную переменную переводят в базис и, выполнив преобразования, получают второй оптимальный план с другим набором базисных переменных 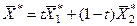 , т.е. будем иметь альтернативный оптимум (рис. 3).
, т.е. будем иметь альтернативный оптимум (рис. 3).
2) Если на каком-либо шаге в разрешающем столбце все коэффициенты будут ais ≤ 0 (т.е. во всех уравнениях будут бесконечные оценочные отношения Θ i = ∞ той переменной xi, которая переводится в основные), то задача не имеет конечного оптимума, целевая функция 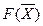 не ограничена на ОДР (Fmax = ∞, Fmin = –∞) и задачу решить нельзя.
не ограничена на ОДР (Fmax = ∞, Fmin = –∞) и задачу решить нельзя.
3) Если в столбце Θ i содержатся два или несколько одинаковых наименьших значений отношения, то новый план будет вырожденным (одна или несколько базисных переменных станут равными нулю). В этом случае следующий шаг не вызовет изменения функции F (Δ F = 0), хотя приведет к новому опорному плану. Наличие «пустых» шагов может привести к зацикливанию, т.е. многократному повторению процесса вычислений, не позволяя завершить задачу. Избежать зацикливания можно с помощью определенных мер, например, способом Креко. Задачи с зацикливанием встречаются редко.
 2015-03-22
2015-03-22 14469
14469
