Решение. Для определения оптимального числа каналов необходимо минимизировать общие потери

Для определения оптимального числа каналов необходимо минимизировать общие потери. Общие потери Z состоят из двух частей - из затрат на эксплуатацию каналов и потерь из-за отказов в соединении с абонентом.

Затраты на эксплуатацию n каналов равны n Ск, и потери от отказов равны произведению Pотк Со 100, где Pотк - вероятность отказа. Поэтому имеем задачу на оптимизацию

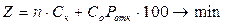(3.21)

Таким образом, необходимо найти целое n, при котором Z имеет наименьшее значение.

Решение типовой задачи системы массового обслуживания (СМО) может быть разбито на следующие этапы:

1. Анализ работы СМО

2. Проверка характеристик входного и выходного потока.

2.1. Проверка соответствия входящего потока требований пуассоновскому закону.

2.2. Проверка соответствия времени обслуживания показательному закону распределения

3. Определение основных характеристик системы в зависимости от способа организации обслуживающей системы по формулам СМО

Находим оптимум решаемой задачи, используя полученные характеристики СМО и зная стоимостные данные.

Анализ формулы (3.21) показывает, что единственной неизвестной величиной является Pотк. Для ее определения воспользуемся формулами теории массового обслуживания. Чтобы их применить корректно, необходимо, установить, что указанная задача относится к указанному классу (к задачам массового обслуживания).

В качестве запроса на обслуживание можно рассматривать запрос на «городской» звонок: запрос удовлетворен, если связь предоставлена; в запросе отказано, если городская линия занята

Для этого проверим соответствие распределение количества заявок на соединение в единицу времени (входящего потока) пуассоновскому закону, а распределение времени обслуживания - показательному закону распределения с помощью критерия согласия Пирсона - χ², с уровнем значимости α =0,05 (теоретические основы его применения приведены в [2]). При проверке по этому критерию сначала определяют меру расхождения фактического распределения с предполагаемым теоретическим:

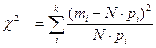, (3.22)

где k – количество разрядов в которые сведены результаты опытов; N – общее количество наблюдений; m_i – количество наблюдений в i -том разряде; p_i – теоретическая вероятность (по предполагаемому закону распределения) i- го разряда.

Для определения величины χ²_крит , которое используется в процедуре проверки, необходимо определить число степеней свободы r:

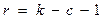, (3.23)

где: с – число параметров распределения. Для пуассоновского и показательного законов распределения с =1.

Все расчеты выполнены с помощью электронных таблиц MS Excel, фрагменты таблиц приведены на рис. 3.12-3.14.

Проверим гипотезу о том, что распределение, представленное в табл. 3.2, является частным случаем распределения Пуассона с уровнем значимости α=0,05. Выдвигаем гипотезу Н_о: данное эмпирическое распределение следует распределению Пуассона. Альтернативная гипотеза – Н₁: эмпирическое распределение не следует распределению Пуассона.

Для вычисления объема выборки (рис.3.12), в ячейку B15 вводим формулу =СУММ(B7:B14), полученное значение 360 и есть искомая величина N.

Распределение Пуассона описывается формулой (3.6), в которой λ – параметр распределения, в данном случае он неизвестен. В качестве оценки параметра λ используем x_ср – среднее значение случайной величины. В ячейке C17 помещаем вычисленное среднее значение по формуле =C15/B15. Получили значение 1,9083 – это и есть оценочное значение λ, которое будем использовать для построения теоретического распределения.

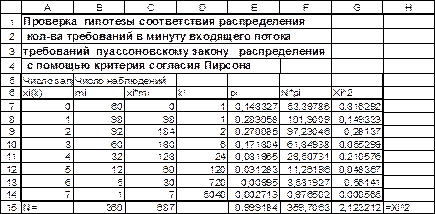
Рис. 3.12. Рабочий лист Excel с расчетами

В интервал E7:E14 заносим теоретические значения вероятности, вычисленные по формуле (3.6) при λ =1,9083. В ячейку E7 заносим формулу =EXP(-$C$17)*($C$17^A7)/D7, в остальные ячейки диапазона эта формула заноситься копированием.

В интервал F7:F14 заносим теоретические значения частот, вычисленные по формуле 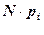. В ячейку F7 заносим формулу =E7*$B$15, в остальные ячейки диапазона эта формула заносится копированием.

Теперь мы готовы вычислить χ² по формуле (3.22). Для этого в ячейку G7 заносим формулу =(B7-F7)^2/F7, в остальные ячейки диапазона G7:G14 формула заносится копированием. Сумму значений ячеек G7:G14 помещаем в ячейку G8 – это искомое значение χ ^2. = 2,1232.

Далее вычисляем число степеней свободы r:

; k = 8, c = 1, r = 6 иα = 0.05,(с - количество определяемых параметров распределения),

χ²_крит = 12,59 (найдено по таблицам, см. Приложение 1).

Поскольку χ² < χ²_крит, то гипотезу H₀ о соответствии количества вызовов в единицу времени (в минуту) пуассоновскому закону принимаем.

Проверим гипотезу о том, что распределение, представленное в табл. 3.3, является частным случаем показательного распределения с уровнем значимости α=0,05. Выдвигаем гипотезу Н_о: данное эмпирическое распределение следует показательному закону распределения. Альтернативная гипотеза – Н₁: эмпирическое распределение не следует показательному закону распределения.

Показательное распределение описывается формулой (3.8), в которой μ - параметр распределения, имеющий смысл интенсивности обслуживания, в данном случае он неизвестен. В силу справедливости соотношения (3.9), в качестве оценки этого параметра m используем 1/ t_ср – величину обратную к среднему значению случайной величины. В интервал ячеек A8:B22 введем начальные и конечные значения интервалов (разрядов), в интервал C8:C22 - поместим значения середин интервалов, для этого в ячейку C8 вводим формулу =(A8+B8)/2, в остальные ячейки интервала эта формула заносится копированием. В интервал ячеек D8:D22 помещаем наблюдаемые значения частот m_i ( количество разговоров)

Далее определяем оценку значения μ, и поскольку оно равно величине обратной математическому ожиданию, определяем t _ср – среднее время обслуживания - среднее значение случайной величины. Для этого в ячейку D23 вводим формулу =СУММ(D8:D22). Полученное значение 250 и есть объем выборки N.

Чтобы вычислить 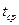, воспользуемся формулой

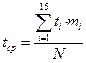(3.24)

где: t_i − середина i -го интервала, 15 –число интервалов.

Для этого вычислим произведения в столбце E8:E22, в ячейку E8 вводим формулу =C8*D8; в остальные ячейки диапазона значения заносим копированием. Далее находим сумму, для этого в ячейку E23 вводим формулу = СУММ(E8:E22). В ячейку E24 помещаем вычисленное среднее значение по формуле =E23/D23, получим значение 1,978.

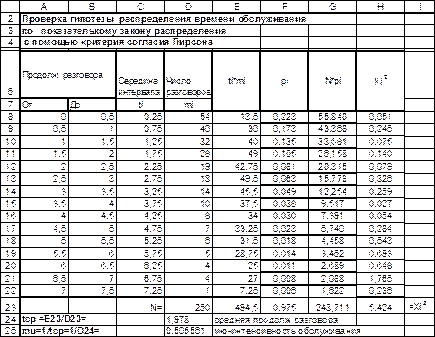
Рис. 3.13. Рабочий лист Excel с расчетами

Далее вычисляем оценку значения μ, для этого в ячейку E25 помещаем формулу =1/E24. Итак, оценочное значение μ равное 0.5056 найдено. Его можно использовать для построения теоретического распределения. Чтобы применить формулу (3.22) нужно знать теоретические значения р_i для каждого интервала. С учетом соотношения (3.5), точное значение р_i равно:

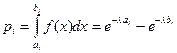, (3.25)

где: a _i и b _i − начало и конец i -го интервала соответственно.

Для этого в ячейку F8 вводим формулу:

=EXP(-$D$25*A8)-EXP(-$D$25*B8)

В остальные ячейки диапазона F8:F22 заносим эту формулу копированием.

В интервал G8:G22 заносим теоретические значения частот, вычисленные по формуле 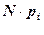. В ячейку G8 заносим формулу =F8*$D$23, в остальные ячейки диапазона эта формула заносится копированием.

Теперь мы готовы вычислить χ² по формуле (3.22). Для этого в ячейку H8 заносим формулу =(D8-G8)^2/G8, в остальные ячейки диапазона H8:H22 формула заносится копированием. Сумму значений ячеек H8:H22 помещаем в ячейку H23 – это искомое значение χ². Получили χ² =5,4245.

Определим число степеней свободы r по формуле (3.23). Поскольку k=15, c=1, то r =13 и α=0.05. χ²_крит = 22,4 (найдено по таблицам, см. Приложение 1).

Поскольку χ² < χ²_крит, то гипотезу H₀ о соответствии данного распределения показательному закону принимаем.

Таким образом, данная СМО может быть исследована аналитическими методами, и для расчета ее показателей могут быть применены формулы теории массового обслуживания.

Переходим ко второму этапу - определению основных показателей. В данном случае обслуживающая система является многоканальной (включает n каналов обслуживания). Данная система - система с отказами, поскольку, если в момент поступления требования нет свободных обслуживающих каналов (т.е. заняты все каналы, так как в системе уже находится n требований), то требование покидает систему не обслуженным. Все состояния системы приведены на рис.3.2:

S₀ – все каналы свободны;

S₁ – один канал занят, остальные свободны;

S₂ – два канала заняты, остальные свободны;

S_k – k каналов занято, остальные (n - k) свободны;

S_n – все n каналов заняты.

Для вычисления основных характеристик системы воспользуемся формулами (3.11)-(3.16).

При решении данной задачи нас главным образом интересует вероятность отказа Pотк, ее вычисление для различных n приведено на рис.3.14. В ячейках B20:B26 приведены значения вероятностей отказа для числа каналов, указанных в ячейках A20:A27.

Переходим к третьему этапу – определению оптимального числа каналов. Это можно сделать несколькими способами, здесь будет приведено два из них - метод перебора и метод целочисленного программирования.

Рис. 3.14. Рабочий лист Excel в режиме отображения данных.

Метод перебора. В этом случае необходимо вычислить величину затрат для каждого из возможных n от 1 до 7. Большее количество каналов рассматривать не имеет смысла, поскольку по результатам предварительного исследования системы только один раз наблюдалась ситуация, когда были затребованы 7 каналов.

Для вычисления величины затрат воспользуемся формулой (3.21) и занесем ее в ячейки C20:C26 (рис.3.14). В ячейку C20 запишем формулу =$F$3*A20+B20*$G$3*100, в смежные ячейки C21:C26 она заносится копированием. По полученным данным строим график зависимости Z от n (рис. 3.15). Анализируя полученные результаты приходим к выводу, что оптимальное количество каналов равно 5, поскольку именно при этом значении величина затрат имеет минимум.

Метод целочисленного программирования. Для реализации этого метода средствами MS Excel необходимо использовать надстройку «Поиск решения». Диалоговое окно этой надстройки показано на рис. 3.16. Для применения этого средства необходимо выразить целевую функцию, в виде формулы MS Excel через искомое значение (n - число каналов), для которой отведем ячейку G20. Первоначально в эту ячейку можно занести любое значение от 1 до 7. Для определенности занесем значение 2. В ячейку E20 запишем формулу для вычисления Pотк (использовано соотношение (3.4)):

=СУММПРОИЗВ(D8:D15;F8:F15)/СУММПРОИЗВ(D8:D15;E8:E15)

Числитель этой формулы равен 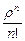, знаменатель -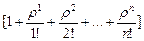

Необычный вид этих формул объясняется тем, что число слагаемых не постоянно, а зависит от n. Поэтому введены два столбца E8:F15, в которых содержатся только нули и единицы. В столбце E8:E15 содержатся единицы для k меньших n, остальные - нули. Для этого в ячейку E8 введена формула =ЕСЛИ($G$20<A8;0;1), в остальные ячейки диапазона эта формула заносится копированием.

В столбце F8:F15 содержится единица только для k равного n ( k = n ), остальные - нули. Для этого в ячейку F8 введена формула =ЕСЛИ($G$20<>A8;0;1), в остальные ячейки диапазона эта формула заносится копированием.

Вычислим значение целевой функции, для этого в ячейку F20 запишем формулу для вычисления величины общих затрат:

=E20*G3*100+F3*G20.

После этого пользуемся надстройкой «Поиск решения» (рис 3.16), заполняя соответствующие поля диалогового окна. Поле ограничений содержит естественные ограничения: число каналов целое ($G$20 = целое) и больше 0 ($G$20>=0). Далее нажимаем кнопку «Выполнить».

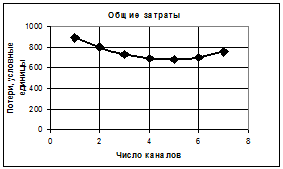
Рис. 3.15. График зависимости Z- величины потерь от n - количество каналов

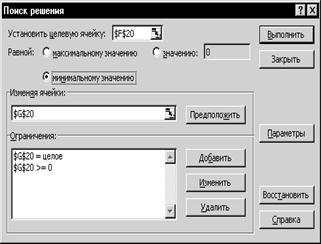
Рис. 3.16. Диалоговое окно надстройки «Поиск решения»

При успешном решении задачи методом целочисленного программирования средствами надстройки «Поиск решения» система выдает диалоговое окно, показанное на рис. 3.17, а в ячейке G20 будет находиться найденное оптимальное значение n = 5, в ячейке F20 будет находиться величина затрат, ему соответствующая (678.834). Результаты решения, полученные двумя методами, совпадают.

Рис. 3.17. Диалоговое окно «Результаты поиска решения» надстройки «Поиск решения»

Для найденного оптимального числа каналов (n =5) определим основные характеристики системы:

1) относительную пропускную способность системы:

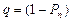= q=1-0.1788=0.8212

2) абсолютную пропускную способность системы:

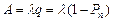=1.9083 × 0.8212= 1.567

3) среднее число занятых каналов:

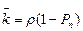= 3.7746 × 0.8212 = 3.10

Выводы:

1. Анализ исходных данных показывает, что задача может быть решена методами теории массового обслуживания.

2. Данная система относится к многоканальным системам без очереди с отказами.

3. Для расчета основных параметров данной СМО применимы формулы Эрланга.

4. При данных стоимостных характеристиках канала и величины потерь из-за отсутствия связи, оптимальным числом каналов является 5.

5. Оптимальное число каналов вычислено методами перебора и целочисленного программирования. Значения полностью совпали.

6. Для найденного оптимального числа каналов (n =5) определены основные характеристики системы:

§ относительная пропускная способность системы: q = 0.82

§ абсолютная пропускная способность системы: А = 1.56

§ среднее число занятых каналов: k = 3.10.

ЛАБОРАТОРНАЯ РАБОТА №3. Моделирование простейшего потока событий.

Лабораторная работа состоит из трех задач. Первые две задачи посвящены углубленному изучению распределений случайных величин, которые используются при моделировании СМО. Эти распределения изучались ранее в курсе высшей математики. Третья задача связана с изучением свойств простейшего потока событий, также использующих эти распределения.