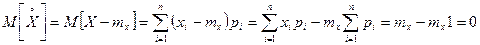1. Функція розподілу F(x) є неспадна функція свого аргументу, тобто при x2>x1 - F(x2)³F(x1)
2. При 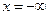 функція розподілу F(x)=0 тобто F(
функція розподілу F(x)=0 тобто F(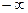 )=0
)=0
3. При 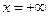 F(x)=1 тобто F(
F(x)=1 тобто F(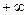 )=1
)=1
4. 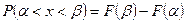
5. Якщо всі значення випадкової величини належать інтервалу (a, b), то
при 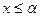 функція розподілу F(x)=0,
функція розподілу F(x)=0,
при 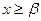 функція розподілу F(x)=1.
функція розподілу F(x)=1.
6. Графік інтегральної функції F(x) розподілу має вигляд
| Дисперсія випадкової величини – характеризує розсіювання випадкової величини відносно математичного сподівання, позначається 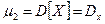 . За означенням: . За означенням: 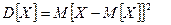 . Для дискретної випадкової величини: . Для дискретної випадкової величини: 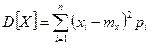 Для безперервної випадкової величини: Для безперервної випадкової величини: 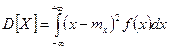 Дисперсія має размірність квадрата випадкової величини. Для наочної характеристики розсіювання зручніше застосовувати величину з розмірністю випадкової величини. Тому з дисперсії добувають корінь, який називають середньоквадратичним відхиленням (СКВ) випадкової величини і позначають Дисперсія має размірність квадрата випадкової величини. Для наочної характеристики розсіювання зручніше застосовувати величину з розмірністю випадкової величини. Тому з дисперсії добувають корінь, який називають середньоквадратичним відхиленням (СКВ) випадкової величини і позначають 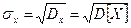 Отже: Отже: 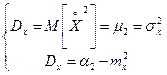 Властивості дисперсії: 1) Властивості дисперсії: 1) 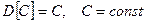 ; 2) ; 2) 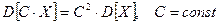 ; 3) ; 3) 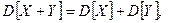 X,Y - незалежні випадкові величини; 4) X,Y - незалежні випадкові величини; 4) 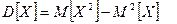 . Інші моменти вищих порядків дають можливість визначити додаткові характеристики розподілу, зокрема характеризують форму кривої розподілу. Це такі як асиметрія і ексцес. Вводяться коефіцієнти асиметрії . Інші моменти вищих порядків дають можливість визначити додаткові характеристики розподілу, зокрема характеризують форму кривої розподілу. Це такі як асиметрія і ексцес. Вводяться коефіцієнти асиметрії 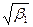 і ексцесу і ексцесу 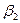 (гостро- чи плосковершинності) розподілу, які визначаються відповідно: (гостро- чи плосковершинності) розподілу, які визначаються відповідно: 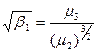 ; ; 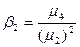 . Задачі для засвоєння матеріалу. Приклад 1. Функція розподілу безперервної випадкової величини задана виразом: . Задачі для засвоєння матеріалу. Приклад 1. Функція розподілу безперервної випадкової величини задана виразом: | | | |
| | | | | |
| | | | | | | | |
| | 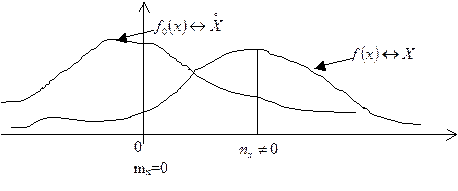 Моменти центрованої випадкової величини називають центральними моментами. Центральний момент k –го порядку випадкової величини Х -це математичне сподівання k –го порядкувідповідної центрованої випадкової величини Моменти центрованої випадкової величини називають центральними моментами. Центральний момент k –го порядку випадкової величини Х -це математичне сподівання k –го порядкувідповідної центрованої випадкової величини 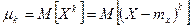 Для дискретної випадкової величини: Для дискретної випадкової величини: 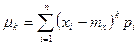 , , 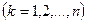 Для безперервної випадкової величини: Для безперервної випадкової величини: 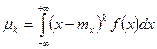 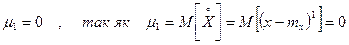 Зв’язок між центральними і початковими моментами різних порядків. Зв’язок між центральними і початковими моментами різних порядків. 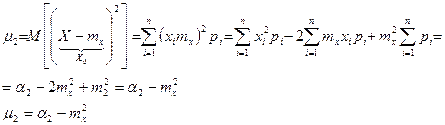 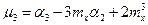 Із всіх моментів в якості характеристики випадкової величини найчастіше використовують перший момент (мат. сподівання) Із всіх моментів в якості характеристики випадкової величини найчастіше використовують перший момент (мат. сподівання) 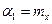 і другий центральный момент і другий центральный момент 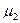 , який називають дисперсією випадкової величини. , який називають дисперсією випадкової величини. | | | 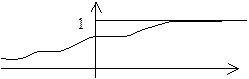 Диференційна функція розподілу – або густина розподілу – це перша похідна від інтегральної функції розподілу Диференційна функція розподілу – або густина розподілу – це перша похідна від інтегральної функції розподілу 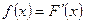 . Властивості: густина розподілу визначена тільки для безперервної випадної величини. . Властивості: густина розподілу визначена тільки для безперервної випадної величини. 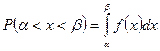 Графік диференційної функції розподілу називають кривою розподілу. Площа обмежена кривою диференційної функції розподілу і віссю абсцис дорівнює 1, і ймовірність попадання результату спостереження і випадкової похибки у заданий інтервал дорівнює цій площі. За кривою розподілу випадкових похибок можна визначити, які значення випадкових похибок більш ймовірні, які менш ймовірні. Функція розподілу результатів вимірювань чи похибок є універсальним способом розміщення випадкових похибок навколо істинного значення, але для їх визначення необхідно проводити складні дослідження і обчислення, тому суттєві особливості випадкових похибок описують за допомогою спеціальних числових характеристик. До них відносяться 1) характеристики положення розподілу результатів похибок: математичне сподівання, мода, медіана; 2) характеристика розсіювання випадкових похибок відносно істинного значення: дисперсія, середнє квадратичне відхилення. 3) моменти розподілу. Найважливішою характеристикою положення є математичне сподівання, яке показує середнє значення випадкової величини Математичне сподівання величини Х позначають М[X] або mx. Для дискретних випадкових величин М[X] визначається як сума добутків відповідних значень на їх ймовірність: Графік диференційної функції розподілу називають кривою розподілу. Площа обмежена кривою диференційної функції розподілу і віссю абсцис дорівнює 1, і ймовірність попадання результату спостереження і випадкової похибки у заданий інтервал дорівнює цій площі. За кривою розподілу випадкових похибок можна визначити, які значення випадкових похибок більш ймовірні, які менш ймовірні. Функція розподілу результатів вимірювань чи похибок є універсальним способом розміщення випадкових похибок навколо істинного значення, але для їх визначення необхідно проводити складні дослідження і обчислення, тому суттєві особливості випадкових похибок описують за допомогою спеціальних числових характеристик. До них відносяться 1) характеристики положення розподілу результатів похибок: математичне сподівання, мода, медіана; 2) характеристика розсіювання випадкових похибок відносно істинного значення: дисперсія, середнє квадратичне відхилення. 3) моменти розподілу. Найважливішою характеристикою положення є математичне сподівання, яке показує середнє значення випадкової величини Математичне сподівання величини Х позначають М[X] або mx. Для дискретних випадкових величин М[X] визначається як сума добутків відповідних значень на їх ймовірність: 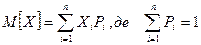 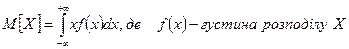 . Теоретико-ймовірнісний зміст математичного сподівання – приблизно дорівнює середньому арифметичному значень випадкової величини: . Теоретико-ймовірнісний зміст математичного сподівання – приблизно дорівнює середньому арифметичному значень випадкової величини: 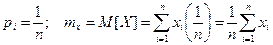 | |
| |
| | | | | |
| | | | | | | | |
| | Властивості математичного сподівання: 1) Математичне сподівання сталої дорівнює сталій 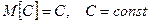 ; 2) ; 2) 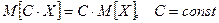 ; 3) ; 3) 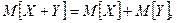 X,Y випадкові величини; 4) X,Y випадкові величини; 4) 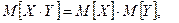 X,Y випадкові величини. Модою (Mod) випадкової величини Х називають її найбільшймовірне значення. За модою розподіл може бути одномодальним та багатомодальним або без модальним (див.рис.3). Одномодальний розподіл – розподіл, коли найбільшу ймовірність має одне значення. Для дискретної випадкової величини. X,Y випадкові величини. Модою (Mod) випадкової величини Х називають її найбільшймовірне значення. За модою розподіл може бути одномодальним та багатомодальним або без модальним (див.рис.3). Одномодальний розподіл – розподіл, коли найбільшу ймовірність має одне значення. Для дискретної випадкової величини. 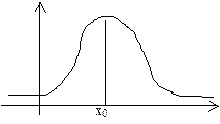 Mod=X3 Рис.3. Одно модальний розподіл. Багатомодальний – конкретніше двохмодальний розподіл представлений на рис. 4. Mod=X3 Рис.3. Одно модальний розподіл. Багатомодальний – конкретніше двохмодальний розподіл представлений на рис. 4. 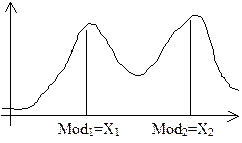 Рис. 4. Двохмодальний розподіл. Медіаною (Med) випадкової величини Х називають таке значення, для якого ймовірність того, що P(X<Med)=P(X>Med). У кожного розподілу Med може бути тільки одна. Med разділяє площу под кривою розподілу на 2 рівні частини. У випадку одномодального і симметричного розподілу mx=Mod=Med, в інших випадках співпадіння немає, див. рис5. Рис. 4. Двохмодальний розподіл. Медіаною (Med) випадкової величини Х називають таке значення, для якого ймовірність того, що P(X<Med)=P(X>Med). У кожного розподілу Med може бути тільки одна. Med разділяє площу под кривою розподілу на 2 рівні частини. У випадку одномодального і симметричного розподілу mx=Mod=Med, в інших випадках співпадіння немає, див. рис5. | | | 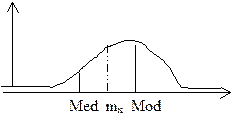 Моменти. Найчастіше для характеристики випадкових величин застосовуються моменти двох видів початкові і центральні. Початковий момент. k-го порядку - дискретной случайной величины Х называется сумма вида: Моменти. Найчастіше для характеристики випадкових величин застосовуються моменти двох видів початкові і центральні. Початковий момент. k-го порядку - дискретной случайной величины Х называется сумма вида: 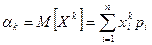 -безперервної випадкової величини Х називаєтся інтеграл виду -безперервної випадкової величини Х називаєтся інтеграл виду 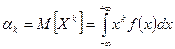 . Очевидно, що математичне сподівання випадкової величини - це початковий момент першого порядку . Очевидно, що математичне сподівання випадкової величини - це початковий момент першого порядку 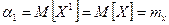 Центрованою випадковою величиною називають відхилення випадкової величини Х від її математичного сподівання: Центрованою випадковою величиною називають відхилення випадкової величини Х від її математичного сподівання: 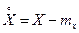 . Математичне сподівання центрованої випадкової величини рівне 0. Для дискретної випадкової величини отримуємо: . Математичне сподівання центрованої випадкової величини рівне 0. Для дискретної випадкової величини отримуємо: 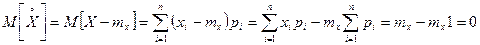 | |
| |
| | | | | |
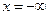 функція розподілу F(x)=0 тобто F(
функція розподілу F(x)=0 тобто F(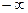 )=0
)=0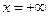 F(x)=1 тобто F(
F(x)=1 тобто F(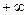 )=1
)=1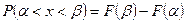
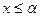 функція розподілу F(x)=0,
функція розподілу F(x)=0,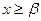 функція розподілу F(x)=1.
функція розподілу F(x)=1.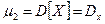 . За означенням:
. За означенням: 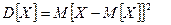 . Для дискретної випадкової величини:
. Для дискретної випадкової величини: 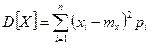 Для безперервної випадкової величини:
Для безперервної випадкової величини: 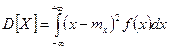 Дисперсія має размірність квадрата випадкової величини. Для наочної характеристики розсіювання зручніше застосовувати величину з розмірністю випадкової величини. Тому з дисперсії добувають корінь, який називають середньоквадратичним відхиленням (СКВ) випадкової величини і позначають
Дисперсія має размірність квадрата випадкової величини. Для наочної характеристики розсіювання зручніше застосовувати величину з розмірністю випадкової величини. Тому з дисперсії добувають корінь, який називають середньоквадратичним відхиленням (СКВ) випадкової величини і позначають 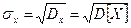 Отже:
Отже: 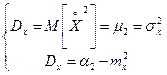 Властивості дисперсії: 1)
Властивості дисперсії: 1) 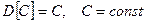 ; 2)
; 2) 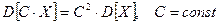 ; 3)
; 3) 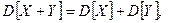 X,Y - незалежні випадкові величини; 4)
X,Y - незалежні випадкові величини; 4) 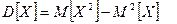 . Інші моменти вищих порядків дають можливість визначити додаткові характеристики розподілу, зокрема характеризують форму кривої розподілу. Це такі як асиметрія і ексцес. Вводяться коефіцієнти асиметрії
. Інші моменти вищих порядків дають можливість визначити додаткові характеристики розподілу, зокрема характеризують форму кривої розподілу. Це такі як асиметрія і ексцес. Вводяться коефіцієнти асиметрії 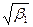 і ексцесу
і ексцесу 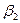 (гостро- чи плосковершинності) розподілу, які визначаються відповідно:
(гостро- чи плосковершинності) розподілу, які визначаються відповідно: 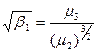 ;
; 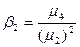 . Задачі для засвоєння матеріалу. Приклад 1. Функція розподілу безперервної випадкової величини задана виразом:
. Задачі для засвоєння матеріалу. Приклад 1. Функція розподілу безперервної випадкової величини задана виразом:  2015-03-22
2015-03-22 789
789
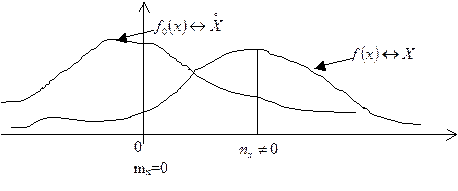 Моменти центрованої випадкової величини називають центральними моментами. Центральний момент k –го порядку випадкової величини Х -це математичне сподівання k –го порядкувідповідної центрованої випадкової величини
Моменти центрованої випадкової величини називають центральними моментами. Центральний момент k –го порядку випадкової величини Х -це математичне сподівання k –го порядкувідповідної центрованої випадкової величини 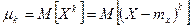 Для дискретної випадкової величини:
Для дискретної випадкової величини: 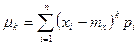 ,
, 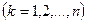 Для безперервної випадкової величини:
Для безперервної випадкової величини: 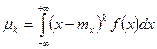
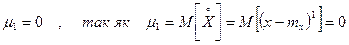 Зв’язок між центральними і початковими моментами різних порядків.
Зв’язок між центральними і початковими моментами різних порядків. 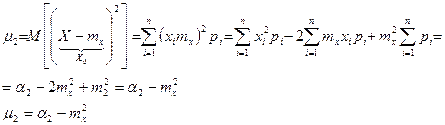
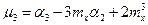 Із всіх моментів в якості характеристики випадкової величини найчастіше використовують перший момент (мат. сподівання)
Із всіх моментів в якості характеристики випадкової величини найчастіше використовують перший момент (мат. сподівання) 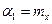 і другий центральный момент
і другий центральный момент 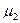 , який називають дисперсією випадкової величини.
, який називають дисперсією випадкової величини.  Диференційна функція розподілу – або густина розподілу – це перша похідна від інтегральної функції розподілу
Диференційна функція розподілу – або густина розподілу – це перша похідна від інтегральної функції розподілу 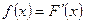 . Властивості: густина розподілу визначена тільки для безперервної випадної величини.
. Властивості: густина розподілу визначена тільки для безперервної випадної величини. 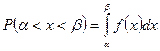 Графік диференційної функції розподілу називають кривою розподілу. Площа обмежена кривою диференційної функції розподілу і віссю абсцис дорівнює 1, і ймовірність попадання результату спостереження і випадкової похибки у заданий інтервал дорівнює цій площі. За кривою розподілу випадкових похибок можна визначити, які значення випадкових похибок більш ймовірні, які менш ймовірні. Функція розподілу результатів вимірювань чи похибок є універсальним способом розміщення випадкових похибок навколо істинного значення, але для їх визначення необхідно проводити складні дослідження і обчислення, тому суттєві особливості випадкових похибок описують за допомогою спеціальних числових характеристик. До них відносяться 1) характеристики положення розподілу результатів похибок: математичне сподівання, мода, медіана; 2) характеристика розсіювання випадкових похибок відносно істинного значення: дисперсія, середнє квадратичне відхилення. 3) моменти розподілу. Найважливішою характеристикою положення є математичне сподівання, яке показує середнє значення випадкової величини Математичне сподівання величини Х позначають М[X] або mx. Для дискретних випадкових величин М[X] визначається як сума добутків відповідних значень на їх ймовірність:
Графік диференційної функції розподілу називають кривою розподілу. Площа обмежена кривою диференційної функції розподілу і віссю абсцис дорівнює 1, і ймовірність попадання результату спостереження і випадкової похибки у заданий інтервал дорівнює цій площі. За кривою розподілу випадкових похибок можна визначити, які значення випадкових похибок більш ймовірні, які менш ймовірні. Функція розподілу результатів вимірювань чи похибок є універсальним способом розміщення випадкових похибок навколо істинного значення, але для їх визначення необхідно проводити складні дослідження і обчислення, тому суттєві особливості випадкових похибок описують за допомогою спеціальних числових характеристик. До них відносяться 1) характеристики положення розподілу результатів похибок: математичне сподівання, мода, медіана; 2) характеристика розсіювання випадкових похибок відносно істинного значення: дисперсія, середнє квадратичне відхилення. 3) моменти розподілу. Найважливішою характеристикою положення є математичне сподівання, яке показує середнє значення випадкової величини Математичне сподівання величини Х позначають М[X] або mx. Для дискретних випадкових величин М[X] визначається як сума добутків відповідних значень на їх ймовірність: 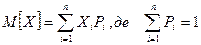
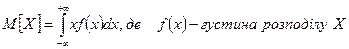 . Теоретико-ймовірнісний зміст математичного сподівання – приблизно дорівнює середньому арифметичному значень випадкової величини:
. Теоретико-ймовірнісний зміст математичного сподівання – приблизно дорівнює середньому арифметичному значень випадкової величини: 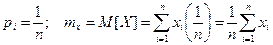
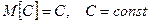 ; 2)
; 2) 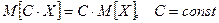 ; 3)
; 3) 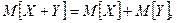 X,Y випадкові величини; 4)
X,Y випадкові величини; 4) 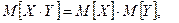 X,Y випадкові величини. Модою (Mod) випадкової величини Х називають її найбільшймовірне значення. За модою розподіл може бути одномодальним та багатомодальним або без модальним (див.рис.3). Одномодальний розподіл – розподіл, коли найбільшу ймовірність має одне значення. Для дискретної випадкової величини.
X,Y випадкові величини. Модою (Mod) випадкової величини Х називають її найбільшймовірне значення. За модою розподіл може бути одномодальним та багатомодальним або без модальним (див.рис.3). Одномодальний розподіл – розподіл, коли найбільшу ймовірність має одне значення. Для дискретної випадкової величини. 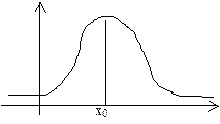 Mod=X3 Рис.3. Одно модальний розподіл. Багатомодальний – конкретніше двохмодальний розподіл представлений на рис. 4.
Mod=X3 Рис.3. Одно модальний розподіл. Багатомодальний – конкретніше двохмодальний розподіл представлений на рис. 4. 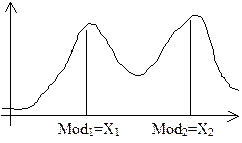 Рис. 4. Двохмодальний розподіл. Медіаною (Med) випадкової величини Х називають таке значення, для якого ймовірність того, що P(X<Med)=P(X>Med). У кожного розподілу Med може бути тільки одна. Med разділяє площу под кривою розподілу на 2 рівні частини. У випадку одномодального і симметричного розподілу mx=Mod=Med, в інших випадках співпадіння немає, див. рис5.
Рис. 4. Двохмодальний розподіл. Медіаною (Med) випадкової величини Х називають таке значення, для якого ймовірність того, що P(X<Med)=P(X>Med). У кожного розподілу Med може бути тільки одна. Med разділяє площу под кривою розподілу на 2 рівні частини. У випадку одномодального і симметричного розподілу mx=Mod=Med, в інших випадках співпадіння немає, див. рис5. 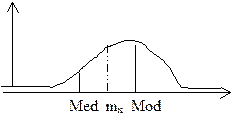 Моменти. Найчастіше для характеристики випадкових величин застосовуються моменти двох видів початкові і центральні. Початковий момент. k-го порядку - дискретной случайной величины Х называется сумма вида:
Моменти. Найчастіше для характеристики випадкових величин застосовуються моменти двох видів початкові і центральні. Початковий момент. k-го порядку - дискретной случайной величины Х называется сумма вида: 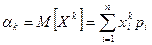 -безперервної випадкової величини Х називаєтся інтеграл виду
-безперервної випадкової величини Х називаєтся інтеграл виду 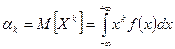 . Очевидно, що математичне сподівання випадкової величини - це початковий момент першого порядку
. Очевидно, що математичне сподівання випадкової величини - це початковий момент першого порядку 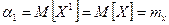 Центрованою випадковою величиною називають відхилення випадкової величини Х від її математичного сподівання:
Центрованою випадковою величиною називають відхилення випадкової величини Х від її математичного сподівання: 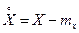 . Математичне сподівання центрованої випадкової величини рівне 0. Для дискретної випадкової величини отримуємо:
. Математичне сподівання центрованої випадкової величини рівне 0. Для дискретної випадкової величини отримуємо: