“Значащими цифрами числа называют все его цифры, кроме нулей, стоящих левее первой, отличной от нуля, цифры, и нулей, стоящих в конце числа, если они стоят взамен неизвестных или отброшенных цифр” (Определение Брадиса Б.М.).
Можно сформулировать иначе: “Значащими цифрами называют все цифры, кроме левых нулей”.
Заметим, что нуль, стоящий в конце десятичной дроби, - всегда значащая цифра (иначе бы этот нуль просто не писали).
Рассмотрим целое приближенное число с нулями справа. Эти нули могут быть значащими или незначащими. Незначащие нули в конце целого приближенного числа можно отмечать каким-либо знаком, например, чертой или другими обозначениями. Лучше вообще не записывать незначащих нулей. Для этого существует два способа:
1. Переход к кратным единицам.
2. Запись результата вычислений или измерений в нормализованной форме (при этом незначащие нули не пишутся).
Если абсолютная погрешность приближенного числа не превышает половины единицы последнего разряда, то все цифры приближенного числа называют верными. Если в приближенном числе все значащие цифры, кроме последней, являются верными, но абсолютная погрешность числа превышает половину единицы последнего разряда, то цифра этого разряда называется сомнительной.
Правило записи приближенного числа (принцип А.Н. Крылова): “Писать число необходимо так, чтобы в нем все значащие цифры, кроме последней, были верны и лишь последняя цифра была бы сомнительной и при этом не более как на одну единицу”.
По принципу Брадиса-Крылова сомнительную цифру сохраняют и в том случае, когда погрешность числа превосходит единицу последнего разряда, но при этом малые значения погрешности более вероятны, чем большие.
Все цифры приближенного числа, следующие за верными и одной сомнительной цифрой, называют неверными.
По принципу Крылова-Брадиса неверные цифры не пишутся.
Число значащих цифр абсолютной погрешности определяется величиной относительной погрешности средней квадратичной ошибки, соизмеримой с абсолютной погрешностью, по следующей формуле [1, 2, 3]:
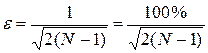 , (1)
, (1)
где ε - относительная погрешность определения средней квадратичной ошибки, примерно равной величине абсолютной погрешности;
N - число измерений.
Например: при N = 25, 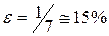 , т.е. относительная погрешность определения квадратичной ошибки (абсолютной погрешности) вычисляется с точностью примерно равной 15 %. Таким образом, если в абсолютной погрешности первая значащая цифра равна или больше 7, то в окончательном результате следует записывать одну значащую цифру, а если меньше 7 - то две значащие цифры.
, т.е. относительная погрешность определения квадратичной ошибки (абсолютной погрешности) вычисляется с точностью примерно равной 15 %. Таким образом, если в абсолютной погрешности первая значащая цифра равна или больше 7, то в окончательном результате следует записывать одну значащую цифру, а если меньше 7 - то две значащие цифры.
Так, если ΔА = 0,7512, то в окончательной форме приводим одну значащую цифру, т.е. ΔА = 0,8 (с учетом округления погрешности с избытком). Если для этого случая (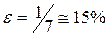 ), ΔА = 0,3671, то в окончательном виде приводим уже две значащие цифры, т.е. ΔА = 0,37 (также с учетом округления с избытком).
), ΔА = 0,3671, то в окончательном виде приводим уже две значащие цифры, т.е. ΔА = 0,37 (также с учетом округления с избытком).
При N = 9 погрешность определения абсолютной ошибки, вычисляемая по формуле (1) 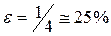 . Следовательно, в окончательной форме необходимо привести одну значащую цифру, если первая значащая цифра абсолютной погрешности равна или больше 4 и две значащие цифры, если первая значащая цифра меньше 4.
. Следовательно, в окончательной форме необходимо привести одну значащую цифру, если первая значащая цифра абсолютной погрешности равна или больше 4 и две значащие цифры, если первая значащая цифра меньше 4.
Например, если ΔА = 0,523, то абсолютную погрешность записываем с точностью до одной цифры ΔА = 0,6. Если ΔА = 0,124, то в окончательной записи следует привести две значащие цифры, т.е. ΔА = 0,13.
Практически при числе измерений N ≤ 15 погрешность округляют до одной значащей цифры, если она больше или равна двум и сохраняют две значащие цифры в остальных случаях. Как видно, такие рекомендации не совсем точны и носят рекомендательный характер. В любом случае видно, что абсолютная погрешность записывается с точностью до одной или двух значащих цифр.
 2015-03-22
2015-03-22 7662
7662








