Рассмотрим обтекание тонкого профиля при малом угле атаки. Течение сжимаемого газа около такого профиля можно исследовать с помощью дифференциального уравнения (5.8), линеаризованного методом малых возмущений:
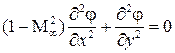 .
.
Это уравнение во всей области течения будет эллиптического типа. К этому же типу относится и уравнение Лапласа (для несжимаемой жидкости). Уравнение (5.8) отличается от уравнения Лапласа только множителем при первом члене, поэтому вполне правомерен вопрос о возможности сведения задачи об обтекании профиля потоком сжимаемой жидкости к задаче обтекания некоторого профиля другой формы потоком несжимаемой жидкости. Приведем уравнение (5.8) к виду уравнения Лапласа. Произведем замену переменных 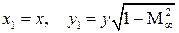 .
.
Тогда 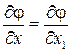 и
и 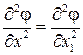 ,
, 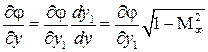 ,
,
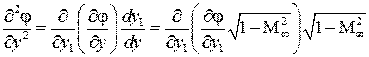 ,
,
т. е.
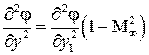 .
.
После подстановки исходное дифференциальное уравнение сводится к уравнению 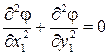 , которое и является уравнением Лапласа.
, которое и является уравнением Лапласа.
Уравнению Лапласа удовлетворяет потенциал скорости потока несжимаемой жидкости. Определив потенциал скорости потока несжимаемой жидкости, через замену переменных 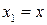 и
и 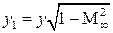 получим скорость потока сжимаемой жидкости.
получим скорость потока сжимаемой жидкости.
При переходе от переменных 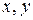 к
к 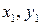 изменяется форма профиля. Допустим, что в плоскости XОY расположен тонкий профиль с хордой
изменяется форма профиля. Допустим, что в плоскости XОY расположен тонкий профиль с хордой 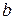 , направленной вдоль оси Х. Профиль обтекает под малым углом атаки
, направленной вдоль оси Х. Профиль обтекает под малым углом атаки 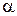 потоком сжимаемой среды со скоростью
потоком сжимаемой среды со скоростью 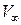 (рис. 8.7). В таком случае в плоскости
(рис. 8.7). В таком случае в плоскости 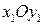 будет какой-то другой профиль с той же хордой (
будет какой-то другой профиль с той же хордой (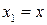 ), но обтекаемый потоком несжимаемой жидкости со скоростью
), но обтекаемый потоком несжимаемой жидкости со скоростью 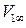 при угле атаки
при угле атаки 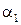 .
.
|
|
 Рассмотрим изменение скоростей в системе координат
Рассмотрим изменение скоростей в системе координат 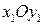 в направлении координатных осей. Так как
в направлении координатных осей. Так как 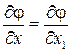 и
и 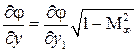 , то
, то 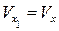 и
и 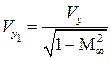 . То есть составляющая скорости по оси X не изменяется, а по оси Y увеличивается в отношении
. То есть составляющая скорости по оси X не изменяется, а по оси Y увеличивается в отношении 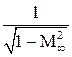 . Это означает увеличение углов наклона касательной к линии тока с осью X, величину которых можно оценить через отношение
. Это означает увеличение углов наклона касательной к линии тока с осью X, величину которых можно оценить через отношение 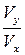 . Следовательно, в этом же отношении увеличивается и угол атаки
. Следовательно, в этом же отношении увеличивается и угол атаки 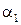 , т. е.
, т. е. 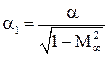 .
. Это же говорит и о том, что исходный контур утолщается, а максимальная толщина профиля 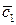 в несжимаемой среде становится равной
в несжимаемой среде становится равной
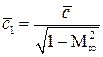 .
.
Таким образом, можно считать, что тонкому профилю в сжимаемой среде соответствует утолщенный профиль в несжимаемой жидкости, обтекаемый под большим углом атаки.
Увеличение угла атаки с одновременным утолщением профиля приводит к увеличению коэффициента подъемной силы профиля 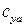 . Следовательно, при известном значении коэффициента подъемной силы профиля в несжимаемом газе
. Следовательно, при известном значении коэффициента подъемной силы профиля в несжимаемом газе 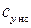 , коэффициент подъемной силы профиля в сжимаемом газе
, коэффициент подъемной силы профиля в сжимаемом газе 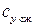 для данного угла атаки при малых скоростях обтекания находится как
для данного угла атаки при малых скоростях обтекания находится как
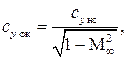 (8.1)
(8.1)
по аналогии, 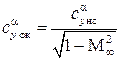 и коэффициент момента
и коэффициент момента 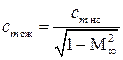 .
.
Коэффициент 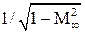 называют поправкой на сжимаемость Прандтля–Глауэрта, а рассмотренный метод учета влияния сжимаемости на аэродинамические характеристики профиля – методом Прандтля–Глауэрта.
называют поправкой на сжимаемость Прандтля–Глауэрта, а рассмотренный метод учета влияния сжимаемости на аэродинамические характеристики профиля – методом Прандтля–Глауэрта.
 2015-03-22
2015-03-22 1136
1136








